模糊加权平均决策模型的结构元求解方法

宫 莉

加权平均在评价决策、工程管理、经济统计等方面有广泛的应用，如决策模型的求解、质量控制等.如果对象的评价值或权重的界限表现不确定，为使决策者以及评价对象本身所具有的模糊性能有效地利用起来，进行综合评价，可以把它们表达成模糊数，进行模糊加权平均，其输出结果就包含有更多的信息，表明了评价结果的各种可能性，为决策者提供更好的依据和参考，对此，文献［1－2］进行了模糊综合评判，但评价结果是各方案满足总目标的隶属函数值，本质上也是一个确定值.BUCKLY、值田等利用模糊集合［3－4］处理类似问题.近些年来，许多学者都对此方面进行了相关研究［5－9］.

目前的论文在利用模糊加权平均法求解决策模型［10］时，大多忽略了模型中系数之间的限定运算问题，求解结果使人难以信服.针对此问题，本文结合模糊结构元理论［11］，首先对模糊加权平均的运算问题进行讨论，然后在此基础上给出了一种随机模拟的求解方法，有效地解决了决策模型中系数的限定性运算问题，便于应用，值得进一步研究推广.

1 模糊数运算及结构元表示

定义1［12］对于模糊集∈F(R)，称为R上的有界闭模糊数当且仅当满足:(1)是正规的，即存在∈R，使得()=1;(2)对于 λ∈(0，1］，={x|(x)≥λ}是闭区间;(3)为有界.记R上的有界闭模糊数全体为F(R).

定义2［13］设E为实数域R上的模糊集，隶属函数记为E(X)，x∈R.如果E(x)满足下述性质:(1)E(0)=1;(2)在区间［－1，0)上E(x)是单增右连续函数，在区间(0，1］上E(x)是单降左连续函数;(3)当－∞ ＜x＜－1或者1＜x＜∞时，E(x)=0.则称模糊集E为R上的模糊结构元.

定理1［13］对于给定的一个正则模糊结构元E和任意的有限模糊数，总存在一个在［－1，1］上的单调有界函数f，使得=f(E).严格地说，存在f的集值延拓，使得=(E)，并称模糊数是由模糊结构元生成的.

定理2［13］若模糊数=f(E)，则的隶属函数为E(f－1(x))，这里 f－1(x)关于变量 x和 y的轮换对称函数(若f(x)是连续严格单调的，则f－1(x)是f(x)的反函数).

若D［－1，1］为区间［－1，1］上同序单调函数全体，定义D［－1，1］上的同序单调变换:

其中 fτ0(x)=f(x)，fτ1(x)=－f(－x)，fτ2(x)=(f(－x)≠0)，fτ3(x)=－(f(x)≠0)(x∈［－1，1］).

定理3［13］设 E 为对称模糊结构元，f和 g 是［－1，1］上的同序单调有界函数，模糊数=f(E)，=g(E)，则有:(1)+=f(E)+g(E)=(f+g)(E);(2)－=f(E)－g(E)=(f+gτi)(E);(3)=f(E)g(E)(fg)(E);当 k 为非负实数时，k=(kf)(E);(4)=f(E)gτ2(E)=(fgτ2)(E).

上述定理证明可参考文献［11－13］.

2 基于结构元理论的模糊加权平均的运算

证明 对于v∈V有

根据Zadeh的扩张原理，对于任意t∈R有

下面证明多元函数 h(v，t)=(v·A)(t)，v∈V，t∈R 是一致连续的.实际上，记 Xv，t={X∈Rn|v·x=t}，则h(v，t)=或 h(v，t)

类似f(v)一致连续性证明，易A(x)证在Rn上一致连续，而Xv，t表示Rn中的连续超平面，对于任意v∈V，根据数学分析的知识，知h(v，t)关于变量t在R上的连续凸函数.同理，可知对于任意t∈R，h(v，t)为关于变量v在V上的连续凸函数.故h(v，t)在v×R上一致连续.

其隶属函数为

所以

3 模糊加权平均决策模型的结构元解法

结合模糊加权运算的结构元理论，来求解模糊加权决策模型，提出一种随机模拟的算法来进行求解，这里给出具体的算法步骤，具体如下:

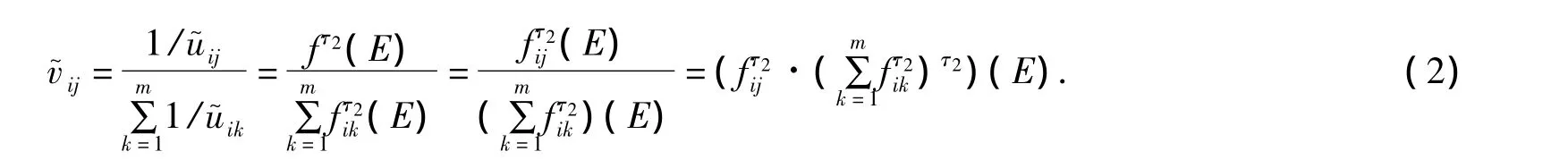
规范化公式为

其中，i=1，2，…，n.

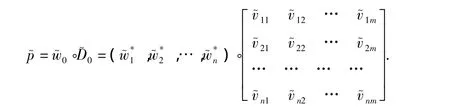
模糊合成算子有很多，根据不同情况选择相应的算子.最常用的模糊合成算子是加权平均，即

根据 qj，j=1，2，…，n 值的大小确定 U 中方案的优劣排序，规则:若 qi≥qj，那么 uiuj，即方案 ui优于方案uj.

若直接利用式(2)代入

计算P值.由于V中的点连续且式中存在连续积分，直接计算运算量很大，需采用数值计算的方式进行近似计算.简化的方法:对V和连续积分进行离散化，用其近似形式代替.设V离散后V'={vk|vk∈V，k=1，2，…，N1}.记离散后的P值为P'.实际上，只要V'中的点在V上分布得足够均匀、点足够多，P'值就能以足够的精度靠近P.

对于如何得到V'，这里提供一种随机数生成的方法:首先，随机生成一个N×n矩阵T=［tij］N×n，其中tij是［0，1］之间的随机数;其次，对矩阵T的行向量进行归一化，设归一化后的随机矩阵为T'=［t'ij］N×n，其中随机矩阵的行向量便组成了V'.易知，V'中的点均匀分布于V上.

4 数值实例

某单位在对干部进行考核选拔时，制定了6项考核指标(因素):思想品德f1、工态f2、工作作风f3、文化水平和知识结构f4、领导能力f5和开拓能力f6，通过群众推荐和评议，对各项指标分别打分，再进行统计处理，从中确定了5名候选人ui(i=1，2，3，4，5).由于群众对同一候选人所给出的指标值(状态值)并不完全相同，因此经过统计处理后的每个候选人在各因素下的状态值是以三角模糊数形式给出的，属性值均为越大越好的效益型，具体的属性值见表1.

表1 候选人在各因素下的属性值及各因素的权重

步骤1 决策矩阵的结构元表示及其规范化.根据表1，容易确定模糊决策矩阵=［］5×6，其中表示对象uj在因素fi下的属性值.由于中每个元素均为三角模糊数，而三角模糊数结构元表示形式为=［aij，bij，cij］=fij(E).其中，fij(x)根据式(2)，得到的规范化矩阵=［gij(E)］5×6，其中 gij(x)=fij(x)·(∑(－x))－1.

步骤2 模糊权重的结构元表示及其规范化.这里模糊权重向量

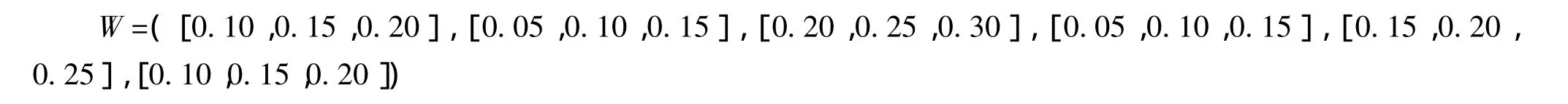
类似于步骤1或(3)式，对W的规范化，得到规范化向量W*.

步骤3 计算P=(p1，p2，p3，p4，p5).这里在近似计算pi值时，V'的随机实值权重向量数N1=1000，数值积分采用梯形数值积分(trapz()函数)，然后，利用编程计算得到表2.

表2 基于随机模拟下的决策排序

步骤4根据pi值大小对5个候选人进行排序结果:u2u1u5u3u4.

5 结语

本文首先结合模糊结构元理论，对模糊加权平均数的运算及其相关性质进行了探讨与研究，并给出具体的证明，然后在此基础上提出了一种随机模拟算法，用以求解模糊加权平均决策模型，并结合模型给出了具体的求解步骤，有效地解决了模型求解过程中参数的限定性运算问题，最后通过数值实例对文中的结论进行了证明.

［1］张跃，邹寿平，宿芬.模糊数学方法及其应用［M］.北京:煤炭工业出版社，1992.

［2］陈湛匀.现代决策分析概论［M］.上海:上海科学技术文献出版社，1991.

［3］植田等.商品评价中AHP与Fuzzy AHP的比较研究［C］∥日本经营工学会平成2年春季大会论文集，1990:127－128.

［4］Buckley J J.Fuzzy hierarchical analysis［J］.Fuzzy Sets and Systems，1985，17(2):233－247.

［5］Xu R N，Zhai X Y.Fuzzy logarithmic least squares ranking method in analytic hierarchy process［J］.Fuzzy Sets and Systems，1996(77):175－190.

［6］Chang D Y.Applications of the extent analysis method on fuzzy AHP［J］.European Journal of Operational Research，1996(95):649－655.

［7］姚敏，张森.模糊一致矩阵及其在软科学中的应用［J］.系统工程，1997，15(2):54－57.

［8］Kwiesielewicz M.A note on the fuzzy extension of Satty＇s priority［J］.Fuzzy Sets and Systems，1998(95):161－172.

［9］Chen CT.Extensions of the TOPSIS for group decision－making under fuzzy environment［J］.Fuzzy Sets and Systems，2000(114):1－9.

［10］徐泽水.对方案有偏好的三角模糊数型多属性决策方法研究［J］.系统工程与电子技术，2002，24(8):9－12，20.

［11］郭嗣琮.模糊分析中的结构元方法(I)，(II)［J］.辽宁工程技术大学学报，2002，21(5):670－673;21(6):808－810.

［12］郭嗣琮.［－1，1］上同序单调函数的同序变换群与模糊数运算［J］.模糊系统与数学，2005，19(3):105－110.

［13］郭嗣琮，苏志雄，王磊.模糊分析计算中的结构元方法［J］.模糊系统与数学，2004，18(3):68－75.