三阶随机占优风险控制下的投资组合优化模型

胡支军，陈 璟，彭 飞

(1.贵州大学理学院，贵州贵阳 550025;2.华南师范大学经济管理学院，广东广州 510631)

0 引言

在金融学中，最优投资组合选择问题无论是在理论上还是在实践中都是重要的研究内容.投资组合的选择通常都是在不确定的环境下发生的，在这种情况下有两种方法常被用来选择投资组合:第一种为Markowitz提出的均值-方差模型及其各种改进.但是，这些模型仅使用两个(或几个)统计量描述收益率的分布，因此可能忽略了重要的信息.第二种方法是随机占优，上世纪60年代发展起来的随机占优(stochastic dominance，SD)［1］是不确定环境下决策理论的一个重要概念.随机占优理论认为，只要投资者对证券(组合)收益的分布函数具有完善的信息，就可以比较各种证券(组合)的优劣，从而确定最优的投资组合.

Dentcheva＆Ruszczynski［2-3］首先引入具有随机占优约束的优化问题，这是在最优化框架下管理风险的一个漂亮方法，在追求期望利润的同时，决策者通过选择随机占优于某个随机基准的方案以规避风险.随后，Dentcheva＆Ruszczynski［4］建立了在投资组合的实际收益率二阶随机占优(SSD)于某个参考随机基准收益率约束下的投资组合优化模型，其目标函数是最大化投资组合的期望收益率.Roman，Darby-Dowman＆Mitra［5］利用多目标规划理论构建了SSD准则下非劣的投资组合，而且组合的收益率分布具有特定的性质.Luedtke［6］则应用优势理论进一步给出随机占优约束下的最优化问题的新的整数和线性规划模型，比Dentcheva＆Ruszczynski［4］的模型更加紧凑.进一步，文献［7］对多维多面体线性SSD约束下的优化问题给出了样本平均割曲面(sample average cutting-surface)算法.最近，Meskarian，Xu＆Fliege［8］则给出了当收益函数不一定是线性函数时具有SSD约束的投资组合优化问题的随机近似方法和水平函数法.

三阶随机占优(TSD)在SSD的基础上，进一步假定投资者表现为递减绝对风险规避，即投资者为了抵消一定的风险而愿意支付的风险溢价随收益的增高而减少，在收益达到较高水平时，投资者倾向于更少地采取风险规避而增加风险资产的投资.借鉴Dentcheva＆Ruszczynski的思想，构建三阶随机占优约束下的投资组合优化模型，以描述具有递减绝对风险厌恶特征的投资者的投资行为，离散分布时该模型可转化为易于求解的二次规划问题.基于随机占优约束下的投资组合模型具有合理的理论基础，所需数据均可以直接获得，与均值–风险模型和效用函数模型相比具有重要的优势.在传统的均值–风险模型中，风险度量的选取具有一定的主观性，而且难以比较两个风险度量之间的优劣性.此外，均值–风险模型仅使用两个(或少数几个)统计量描述风险资产的收益率分布，可能忽略重要的信息.类似地，最优化期望效用则需要给出效用函数的具体表达式，而实际中往往难以引出投资者的效用函数.随机占优约束下的投资组合模型只需要确定一个合理的随机基准，例如市场指数，从而避免了均值–风险模型和期望效用最大化模型的这些困难.最后，通过上海证券市场的实际数据验证了该模型的有效性与实用性.

1 二阶随机占优约束下的投资组合模型

在投资组合选择的研究中，最为广泛的是构建均值-风险模型，这类模型使用两个统计量―期望值和风险值描述和比较随机变量.均值-风险模型的一般框架为

其中:x表示投资于各个证券的资金量或财富比例而构成的投资决策向量;μ0表示期望收益的目标值;Reward(x)表示投资决策x下的期望收益;Risk(x)则代表投资决策x对应的风险;X表示不同的市场摩擦或投资环境对x所引入的其他约束集.不同的投资者会选用不同的风险度量函数Risk(·).

与均值-风险分析方法相比，随机占优方法实质上是一个多准则模型，它无需对投资组合收益的概率分布做任何假设，也不需要对投资者效用函数的形式做任何限制(尽管在基于投资者效用函数定义各阶随机优势时，需对效用函数的可微性做某些假设).因此，随机占优方法具有很广泛的适应性，可用于众多不确定性因素的比较，已被广泛地应用于经济学和金融学的研究［1］.

在随机占优方法中，随机变量是通过对由他们的累积分布函数所递归定义的绩效函数的逐点对比来进行比较.具体地，设R和R'表示累积分布函数分别为F(·)与G(·)的两个随机变量，称R一阶随机占优于R'，记为R≥FSDR'，如果

进一步，称R二阶随机占优于R'，记为R≥SSDR'，如果

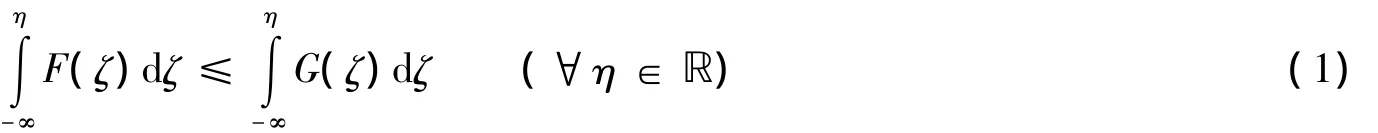
根据文献［1］，R≥SSDR'当且仅当 E［u(R)］≥E［u(R')］.

对任意的非减的凹效用函数u:R→R都成立.因此，如果R≥SSDR'，则任意的理性且风险厌恶的决策者都将偏好于选择R而不是R'.

记R(x)和R(y)分别表示投资组合x和y的随机收益率，称一个投资组合x二阶随机占优于另一投资组合y，如果R(x)≥SSDR(y).一个投资组合x称为在投资组合集X中是SSD有效(或FSD有效)的，如果不存在y∈X，使得(或R(y)≥FSDR(x)).

假设可以获得某个具有有限期望值的基准随机收益率Y，例如对某些基准投资组合有Y=).可能是某个市场指数或投资者的当前投资组合.风险规避的投资者的目的是要构造一个新的投资组合x，使其收益率R(x)二阶随机占优于基准组合的收益率Y.

Dentcheva ＆ Ruszczynski［4］构造了下面的优化问题

其中:f:X×Ω→R是x和ξ的凹连续函数，ξ:Ω→Ξ⊂Rk是定义在支集为Ξ的概率空间(Ω，F，P)上的一个随机向量.特别地，可以取f(x，ξ)=E［R(x，ξ)］，这里E表示取关于ξ的概率分布的期望值，且由于引入了随机占优约束(3)，该优化问题具有非平凡解.模型(2)～(4)具有两大优点:首先，模型的所有数据均可以直接获得;其次，由约束(3)所定义的集合是凸的［2-4］，在离散分布情形可以转化为线性规划问题［4，6］.

2 三阶随机占优约束下的投资组合模型

模型(2)～(4)只适用于一般的风险厌恶型决策者，而对于具有递减绝对风险厌恶型投资者，则需要对该模型做进一步的精炼.

根据文献［1］，称R三阶随机占优于R'，记为R≥TSDR'，如果

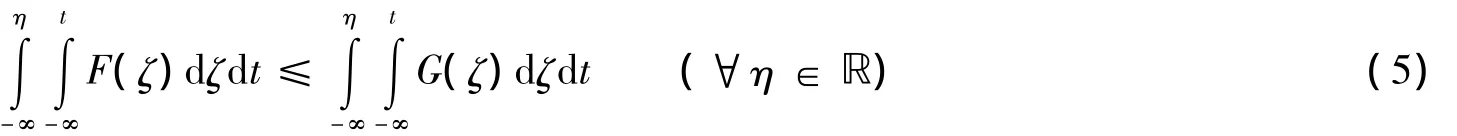
类似地，称投资组合x三阶随机占优于另一投资组合y，如果R(x)≥TSDR(y).一个投资组合x称为在投资组合集X中是TSD有效的，如果不存在y∈X，使得R(y)≥TSDR(x).

根据文献［1］，R(x)≥TSDR(y)当且仅当E［u(R(x))］≥E［u(R(y))］.

对任意非减的满足u‴＞0的凹效用函数u:R→R都成立.因此，如果R(x)≥TSDR(y)，则任意的理性且绝对风险厌恶递减的决策者都将偏好于选择R(x)而不是R(y).

设投资者的资产组合由n种资产构成，资产Sj的随机收益率为rj(j=1，…，n)，并假设收益率(r1，…，rn)分布于一个离散样本空间且用rjt表示j种资产在第t(t=1，…，T)时期的实现值，rj取值rjt的概率为pt=1 T.令xj表示初始财富中投资于资产Sj的比例，一个简单的投资可行集定义为

假设可以获得某个具有有限期望值的基准随机收益率Y=R(z)，z为某个参考投资组合.递减绝对风险厌恶型投资者的目的是构造一个新的投资组合x，使其收益率三阶随机占优于Y.类似于模型(2)～(4)的思想，本文提出下面的投资组合优化模型

具体地，可以令f(x)=E［R(x)］，或某些其它的目标函数［7］.

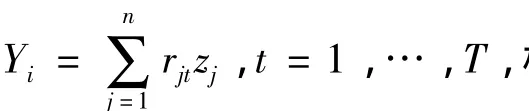
定理3.1，约束条件(7)等价于

令sit=max(Yi-R(x)，0)，表示在时间t时投资组合收益率R(x)小于Yi的差额，i=1，K，M，t=1，K，T.同理，令wit=max(Yi-Y，0)，则模型(6)～(8)可以转化为:

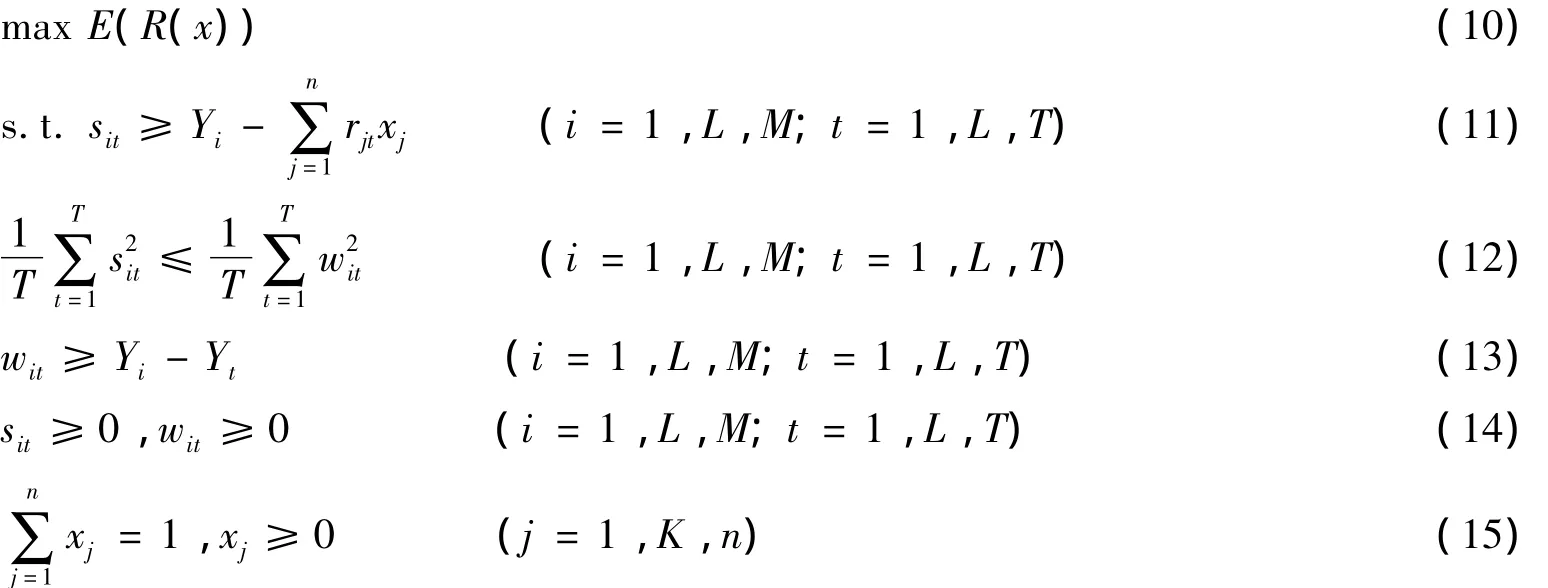
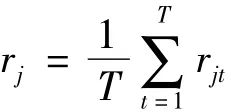
3 实证分析

3.1 样本股票的选取及数据说明

为检验模型(10)～(15)的有效性和实用性，从上海证券市场的不同行业随机选取30只股票.从2009年1月至2011年2月11日共两年108周的周收益率数据作为样本.数据来自RESSE锐思金融研究数据库，这些股票的代码分别为:600 177、600 183、600 186、600 199、600 202、600 221、600 230、600 240、600 249、600 333、600 352、600 363、600 379、600 388、600 420、600 016、600 055、600 114、600 613、600 624、600 704、600 717、600 747、600 783、600 983、600 990、000 021、000 301、000 026、000 886.同时，选择上证180指数从2009年1月至2011年2月共两年108周的周收益率(分别用Y1至Y108表示)作为基准收益.即在模型(10)～(15)中M=T=108，n=30.此外，为了比较三阶随机占优约束下的投资组合模型与二阶随机占优约束下的投资组合模型的区别，借鉴Luedtke［6］的方法将模型(2)～(4)转化为相应的线性规划模型然后利用上述样本数据进行求解.

3.2 计算结果及分析

利用Matlab软件分别求解TSD约束下的模型(10)～(15)和SSD约束下的模型(2)～(4)，计算得到的最优投资组合如表1和表2所示.

表1 TSD约束下的最优投资组合Tab.1 Optimal portfolio with TSD constraints

表2 SSD约束下的最优投资组合Tab.2 Optimal portfolio with SSD constraints

由表1、表2知，TSD约束下的模型(10)～(15)与SSD约束下的模型(2)～(4)(以下分别简记为TSD模型和SSD模型)所确定的最优投资组合不同，SSD模型仅投资6只股票，而TSD模型则投资10只股票.

根据表1和表2所给出的最优投资方案，分别利用这些股票在2011年2月18日至2011年8月12日的周收益率数据检验这两个模型的投资效果.图1给出分别投资于TSD模型和SSD模型的优化组合所获得的收益率，以及同一时期上证180指数的收益率.

由图1可以看出由TSD模型构造的投资组合在样本期外的收益率总体上要优于SSD模型和上证180指数的收益率.为进一步考察TSD模型与SSD模型的投资效果，分别按照下面两个式子计算样本期外的跟踪误差和投资组合的超额收益率:

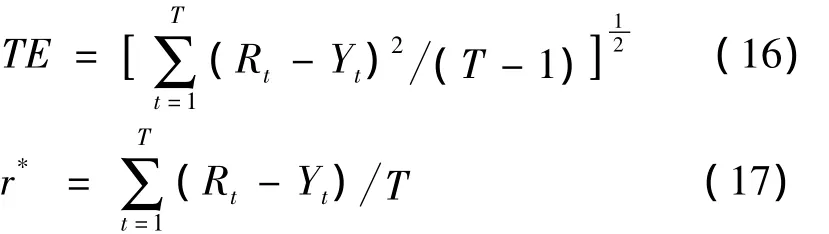
其中:Rt表示投资组合在时期t的收益率;yt为上证180指数在时期t的收益率.经计算得到TSD模型的跟踪误差TE的值为0.026 1，而SSD模型的跟踪误差TE的值为0.016 9，TSD模型的超额收益率r*的值为0.011 2，SSD模型的超额收益率则为-0.002 1，这表明本文所构建的TSD模型在样本期外的跟踪误差虽然比SSD模型的跟踪误差略大，但TSD模型能获得一定的超额收益，SSD模型的超额收益率却为负.上述计算结果表明，本文构建的TSD模型相比较于SSD模型和上证180指数来说具有更好的投资表现.

图1 样本期外优化组合的收益率与上证180指数的收益率Fig.1 Out of Sample returns of optimal portfolio and Shanghai 180 index

4 结语

本文构建了三阶随机占优约束下的投资组合优化模型，该模型在投资组合的收益三阶随机占优于某个基准收益(如市场指数)的约束下最大化投资组合的期望收益率，以反映具有递减绝对风险厌恶特征的投资者的投资行为，离散分布情形该模型可以转化为容易求解的二次规划模型.利用上海证券市场的实际交易数据对模型进行了实证检验，计算结果表明三阶随机占优风险控制下的投资组合模型能够在保持较小跟踪误差的情况下获得一定的超额收益率，具有比SSD模型更好的投资表现.研究结果不仅对提高指数基金的业绩提供了重要的理论依据，而且对指数基金管理也具有重要的现实借鉴意义.