广义非线性Schrödinger方程的半显式多辛拟谱格式

黄浪扬

(华侨大学数学科学学院，福建泉州 362021)

0 引言

考虑如下广义非线性Schrödinger方程的周期初边值问题

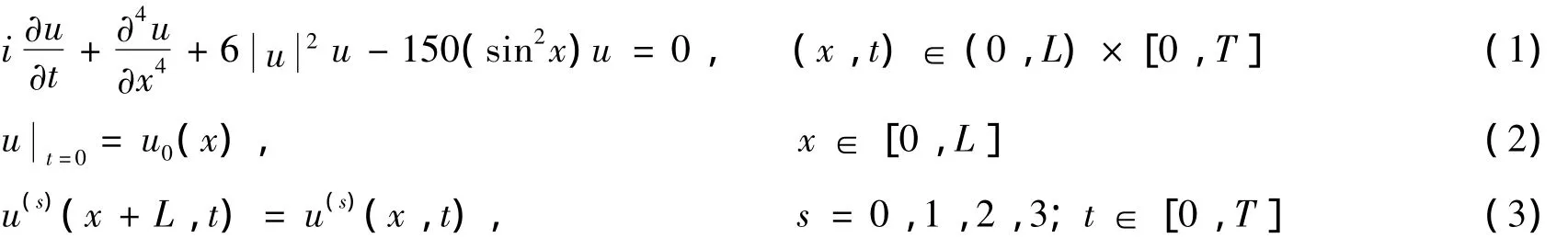
在物理学等学科中，对非线性偏微分方程，特别是非线性Schrödinger方程的多辛几何算法［1-6］的研究已经很多，但对于(半)显式的多辛几何算法［6-9］并不多.本文先给出广义非线性Schrödinger方程(1)的多辛方程组，并对其系数矩阵进行分裂，再采用数值离散方法推导出一个半显式多辛拟谱格式.最后，通过数值例子验证算法的有效性.

1 多辛方程组

首先给出Bridges和Reich的多辛积分［10-11］的概念.很多偏微分方程可改写成为多辛方程组的形式:

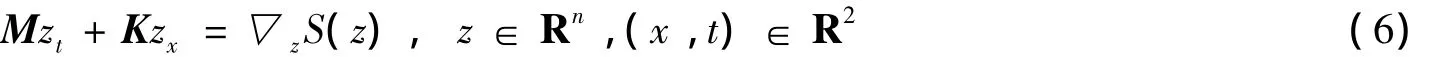
其中:M，K为Rn(n≥3)上的反对称矩阵;▽z是光滑函数S:Rn→R的梯度算子.式(6)具有的一个重要性质为多辛守恒律

设u=a+i b，这里a和b均为实值函数，则式(1)可写成实值方程组

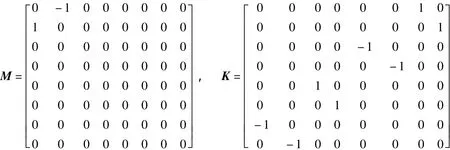
其多辛守恒律为

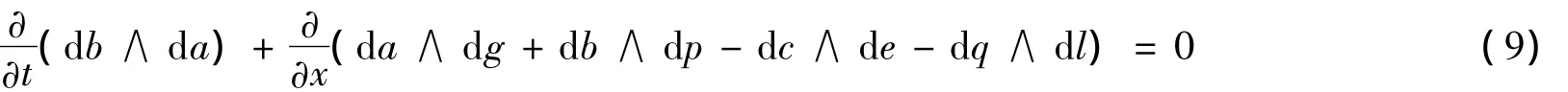
2 半显式多辛拟谱格式

先设时间步长τ＞0，空间步长h=L/N.记tn=nτ，n=0，1，2，…;xj=jh，j=0，1，2，…，N-1(N为偶数).精确解u(xj，tn)=u(jh，nτ)在网格点(xj，tn)处的近似值记为unj.

由拟谱方法的一些主要结果［9，12-13］，设z(x，t)是周期为L的光滑函数，用INz(x，t)来表示z(x，t)在xj点的插值近似，则有

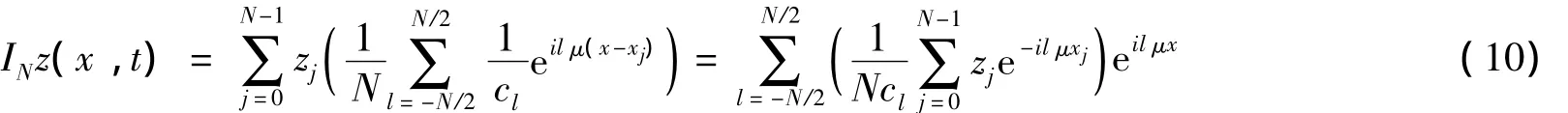
把式(10)代入式(6)，且要求式(6)在xj点精确成立，可得到一个关于zj的方程

这里主要的一步是偏导数∂kINz(x，t)/∂xk在xj点的值表示为zj，采用的方法是对式(10)求微分，计算出它在xj点的数值，从而有

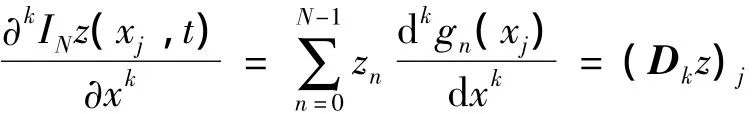
应用上述的Fourier拟谱方法于式(6)，可得

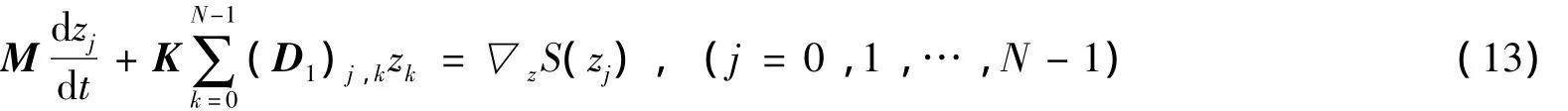
在时间方向用辛Euler方法对式(13)进行离散，得广义非线性Schrödinger方程的半显式多辛拟谱格式:

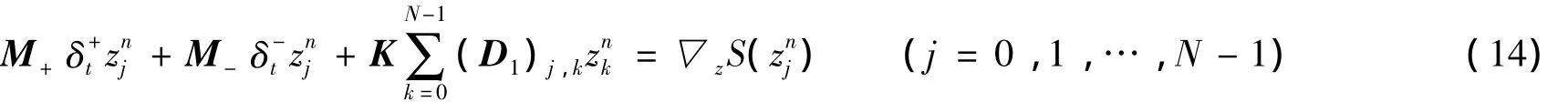
其中:δ+t与δt分别为向前和向后差分算子，即

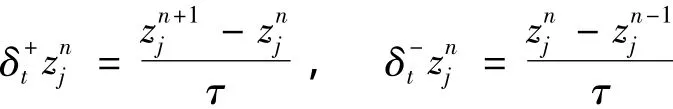
且M+与M-分别为辛阵M的分裂阵，即:M=M++M-，MT+=-M-.这里，M+是上三角矩阵.

定理 半显式多辛拟谱格式(14)具有N个全离散的多辛守恒律

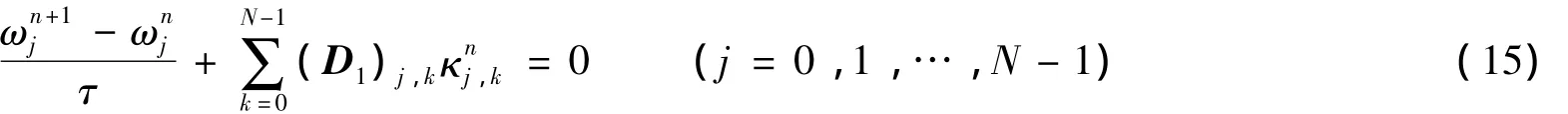
其中:ωnj=dzn－１jΛM+dznj，ｋnj，k=dznjΛK d znk.

证明 式(14)的变分方程为:

用dznj与式(16)作外积，注意到dzn

jΛSzz(znj)dznj=0，即可得全离散的多辛守恒律式(15).

为了计算方便，消去式(14)中的c，q，e，l，g及p，有

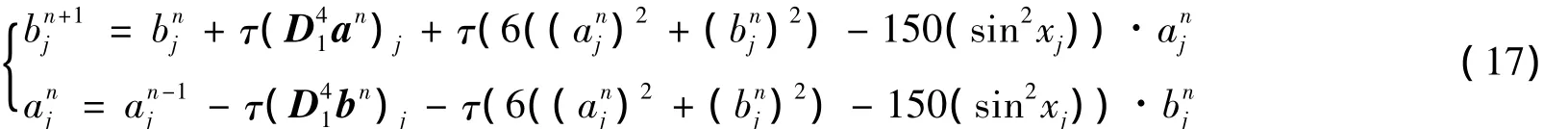
其中:a=(a0，…，aN-1)T，b=(b0，…，bN-1)T，D41表示(D1)4.

把式(17)第二行中的n用n+1替代，得到与式(14)等价的一个多辛拟谱格式

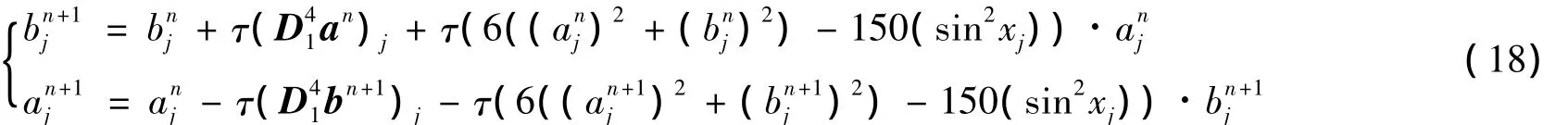
在数值计算中，式(18)的第一行是完全显式的，第二行须在每一时间层上求解一个非线性的方程组，从而是一个半显式多辛拟谱格式.

3 数值例子

图1给出了由式(18)所算得的整体误差随时间t的变化情况.

为了考察数值格式的长时间守恒性质，定义离散电荷误差与离散能量误差分别为:

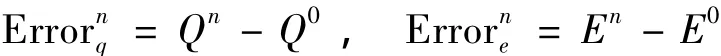
由以上数值结果可知，利用格式(18)长时间数值计算后，整体误差仍很小，且离散电荷误差与离散能量误差还能保持在10-3级，说明该格式适合于长时间的数值模拟.

图1 整体误差Fig.1 Global error

图2 离散误差Fig.2 Discretization error