相互近邻域的函数型回归估计

黄收友



相互近邻域的函数型回归估计

黄收友

(北京航空航天大学 数学与系统科学学院，北京 100083)

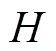
希尔伯特空间；相互最近邻域；回归函数；相容性

1 引言

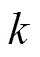
2 相互近邻域的相容性

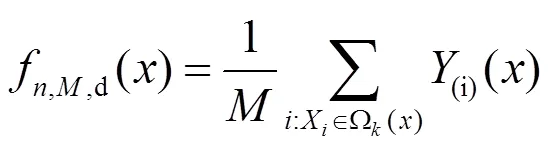
根据这种方法得到相应的估计函数和误差分别为

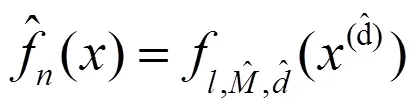
下面给出本文的主要结论:

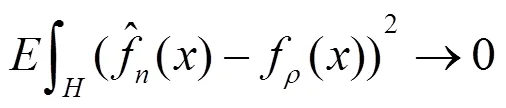
3 证明

在本节中, 我们将阐述相关定理和命题，另外，给出了两个相关的引理命题的证明.

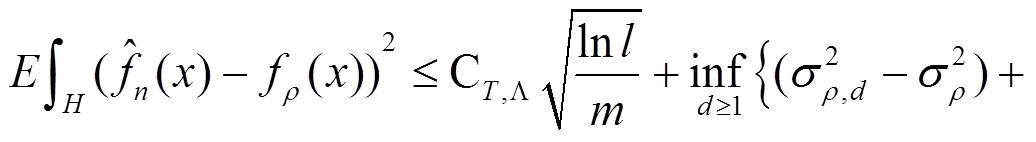
注: 不等式（1）右边的第一项可以看作是逼近误差, 是因为用有限维空间去逼近样本点空间产生的. 由下面引理1和引理2，我们可知上述不等式的第一项和第二项都收敛到零.

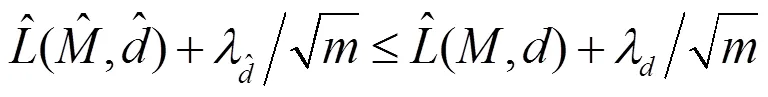
从而可得

进一步, 根据可数个随机事件之并的概率不超过其概率之和，以及Hoeffding不等式可得

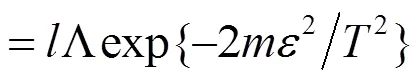
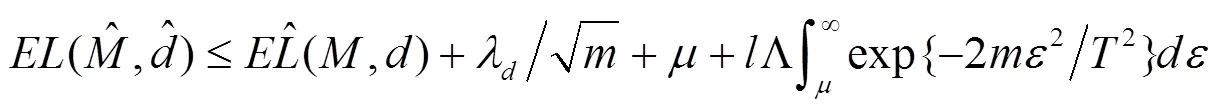
注意到

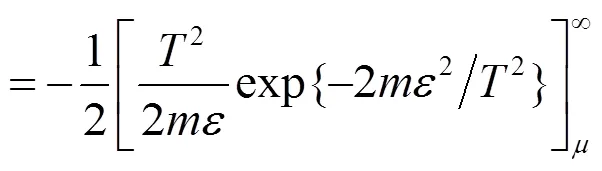
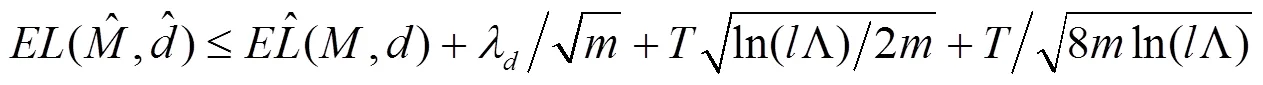
在证明定理1之前, 我们先给出两个引理.

具体证明可以参照文献[6]中的定理6.1.

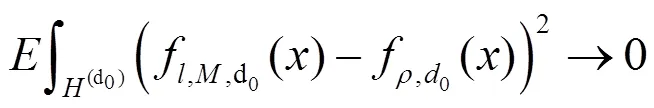
利用命题1, 则有

4 结论

[1] Arnaud G., Nick H．On the mutual nearest neighbors estimate in regression[J]．Journal of Machine Learning Research， 2013，(14)：2361-2376．

[2] Biau G., Buena F., Wegkamp M．Functional classification in Hilbert Spaces[J]．IEEE Transactions on Information Theory，2005，(51)：2163-2172．

[3] Burba F., Ferraty F., Vier P．k-NearestNeighbour method in functional nonparametric regression[J]．Journal of Nonparametric Statistics，2009，(21)：453-469．

[4] Chidananda K., Krishna G．Agglomerative clustering using the concept of mutual nearest neighbourhood[J]．Pattern Recognition，1978，(10)：105-112．

[5] FIX E., Hodges J．Discriminatory Analysis. Nonparametric Discrimination: Consistency properties[J]．International Statistical Review，1989，57(3)：238-247.

[6] Kohler M., Krzyzak A., Walk H．A distribution-free theory of nonparametric regression[J]. Springer Series in Statistics, 2002, XVI: 650.

[7] Stone, C．Consistent nonparametric regression[J]．The Annals of Statistics，1977，(5)：595-645．

A Mutual Nearest Neighbor Estimate for Functional Regression

HUANG Shou-you

(School of Mathematics and System Science, Beihang University, Beijing 100083, China)

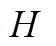
Hilbert Space; Mutual Nearest Neighbor; Regression Function; Consistency

黄收友（1982-），男，博士研究生，研究方向：统计学习理论.

国家自然科学基金（11171014和91130009）；国家重点基础研究发展计划项目（973-2010CB731900）.

O212.4

A

2095－414X(2014)06－0082－04