基于偏最小二乘回归的森林蓄积量遥感估测

刘琼阁，彭道黎，涂云燕

（北京林业大学 林学院，北京100083）

基于偏最小二乘回归的森林蓄积量遥感估测

刘琼阁，彭道黎，涂云燕

（北京林业大学 林学院，北京100083）

森林蓄积量受遥感因子与地形因子的影响，但这些因子间存在多重相关性，会影响模型稳定性与精度。针对森林蓄积量遥感估测自变量间存在多重共线性问题，采用异于传统最小二乘的偏最小二乘方法建立密云县森林蓄积量遥感估测模型。先对可能影响蓄积量的因子进行分析，选取既存在相关性又对模型显著性有影响的因子为森林蓄积量估测的自变量。用预留的样本对模型进行检验，预测值与实测值相比精度达到90.1%。将通过检验的模型对整个密云县进行反演，得到密云县估测森林蓄积量为2 447 695.203 m3。

森林蓄积量；遥感因子；地形因子；多重相关性；偏最小二乘

森林是地球上最大的陆地生态系统，是地球上的基因库、碳贮库、蓄水库和能源库，在全球生态系统平衡中发挥着重要作用，是人类和多种物种赖以生存和发展的基础，其数量与质量是决定森林经济效益与生态系统服务功能的关键。森林蓄积量是衡量一个国家森林健康与否的重要标志，也是政府掌握国家森林资源状况和制定计划采伐、森林经营管理措施的重要依据。传统的蓄积量的测定主要是通过全国森林资源一、二类清查获得数据，存在工作量大，耗时，需要经费多等问题，且调查间隔期长，一类5 a，二类10 a[1]。因而，寻求一种技术上适用，经济上可行的森林资源监测方法，将是一项非常重要的工作。近十年来航天遥感（RS）、地理信息系统（GIS）与计算机的发展以及与数学模型的结合应用，为森林蓄积量的估测带来了新的发展方向，为森林资源的快速监测,实现实时的森林资源状况分析、评价带来了新的方法。

目前，通过遥感图像估测森林蓄积量已成为森林资源调查研究的热点之一。主要用于建模的方法有多元线性回归模型与描述非线性关系的KNN法与人工神经网络模型[2-4]。在实际建模过程中，选用线性回归时，遥感波段及比值波段间可能存在一定程度的多重相关性，这种相关性将使模型稳定性变差。且待定参数的估计方差会随着各自变量间相关程度的增加而增加，最终导致参数估计精度降低[5-6]。对非线性而言，KNN方法靠临近样点观测数据来估算森林生物量，样点的分布会直接影响估测的结果，且计算量很大。后来人工神经网络被引用到了森林蓄积量的估测中，可以避免假设模型不正确造成不利影响，但其黑箱操作，无法表达和分析被预测系统的输入和输出间关系，因而也难于对求得数据做统计检验[7]，且神经网络的方法还停留在样本建模上，对整个遥感图像的估测实现还有待研究。针对自变量间共线性问题，有学者提出岭估计、偏最小二乘[8]。但是岭估计中的岭参数选取受主观影响大。在对研究区及数据规律不了解的情况下不宜采用。因此本研究针对研究区的具体情况，提取样地点的遥感和地学因子，分析其与森林蓄积量的相关关系后，采用偏最小二乘法（PLS）建立遥感估测模型，探讨基于遥感和地学信息的森林蓄积量遥感估测方法。

1 研究区概况

密 云 县 (东 经 116°39′33″～ 117°30′25″， 北纬 40°13′7″～ 40°47′57″)位于北京市东北部，总面积2 229.45 km2，处在燕山山脉和华北平原的交接点，从东南至西北依次与平谷、顺义、怀柔三区接壤，北部和东部分别与河北省的滦平、承德、兴隆三县。是从华北平原通往东北、内蒙古的主要通道，是北京建设中国特色世界城市的绿色屏障。有华北第一大水库之称的密云水库就位于密云县的中部，它是首都重要饮用水源地和生态涵养发展区。密云县属暖温带半湿润半干旱大陆性季风气候区，四季分明，年平均气温10 ℃，年平均降雨量约660 mm，降雨主要集中在6 ～ 9月。其植被属于针阔混交林森林植被带，现存植被主要为人工林以及一些次生植被类型。全县林木生态覆盖率达76.23%，主要森林类型有：侧柏林Platycladus orientalis、杨树Populusspp.、油松林Pinustabulaeformis、 栎 林Quercusspp.、 刺 槐Robinia pseudoacacia、桦木Betulaspp.、核桃楸Juglans mandshurica、五角枫Acer mono等[9]。

2 数据预处理

2.1 图像校正

获得2006年7月12日北京市TM遥感影像，该数据为多光谱数据，分辨率30 m。用2004年已校正的北京遥感影像作为参考影像对2006年遥感图像进行几何校正。选取控制点数为18个，误差控制在0.5个像元内，重采样方法用最近邻点法。并利用密云县行政区界进行不规则剪切得到密云县2006年TM影像。

影像上直接读到的实际是像元灰度值（DN），为了提高分类的精度，有必要对不同时相的影像进行归一化性质的辐射校正[10]。任何尝试将传感器记录的亮度值转换成地面反射的校正模型都必须考虑传感校正参数（地面站已进行过辐射粗校正）及在从太阳到地球再到传感器的复杂路径上影响太阳辐射的众多因子，剔除与地物反射无关的干扰。校正方法可分为两种：相对辐射校正和绝对辐射校正。相对辐射校正的方法有三种：（1）以红外波段最低值来校正可见光波段；（2）回归法；（3）相对散射模型法。绝对辐射校正是将图像的DN值转换为真实地表反射率，需要获取影像过境时的地表测量数据，并考虑地形起伏等因素来校正大气和传感器的影响，目前大多数遥感图像都无法满足上述条件。本研究利用头文件里的信息与USGS网站的文献[11]中给出的标准的行星反射率计算公式（1）与公式（2）和相关的参数取值表将影像灰度值转换为了地表反射率，即完成了绝对辐射校正。

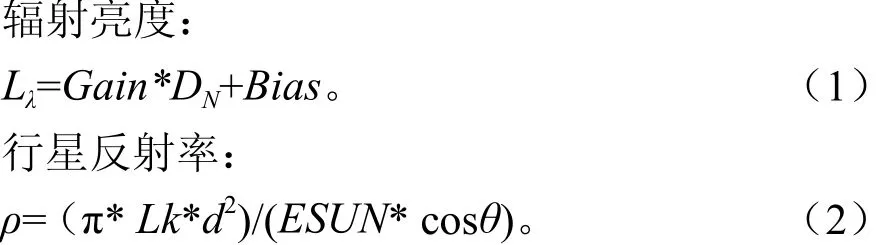
式（1）和式（2）中DN为图像的像元灰度值，无量纲。Gain是增益，Bias是偏置，其单位与辐射亮度一样W·m-2sr-1um-1。d为日地距离参数，ESUN太阳光谱辐射量，θ为太阳天顶角=90-太阳高度角。其中增益、偏置、太阳高度角在头文件中，太阳光谱辐射量来自USGS网站。

在ERDAS 的Model Maker 中将图像按公式（1）与（2）对图像进行代数运算完成图像的绝对辐射校正。在GIS中提取各波段反射率值，并结合一类调查资料及相关档案材料，ARCGIS、ERDAS、SPSS等软件，对数据进行处理。

2.2 样地数据处理

试验中选取一类调查测树点90个，样地均匀分布。用基于聚类的分层抽样抽取60个样地作为建模数据，剩余30个样地作为检验样本。查阅相关文献后，在前人研究与经验知识基础上[12-15]，选取可能影响蓄积量的RS信息与蓄积量进行相关性和自变量间共线性分析。分析信息如下：

表1 各因子相关信息†Table 1 Correlation information of factors

从相关信息表知所选自变量与蓄积量都存在一定相关性，其中TM4、TM5波段及坡向与蓄积量相关性较低，但线性回归模型不仅要考虑与因变量的相关性，还要考虑模型显著性与方差残差。在SPSS里将以上自变量强制选入模型中，根据R2不断调整自变量组合，最后确定自变量组合为坡度、海拔、郁闭度、TM1、TM2、TM3、TM4、TM5、TM7、NDVI、比值、TM(4+5-2)/(4+5+2)、湿度、绿度。从方差扩大因子知遥感各波段间存在严重多重相关性。

3 偏最小二乘原理

偏最小二乘回归方法把主成分分析与典型相关分析有机结合起来，能克服传统自变量间多重共线性的问题，同时提取出的信息能很好的解释因变量。其基本思路如下[16-19]：

设已知单因变量y和自变量[x1,x2,…,xp]，样本个数n，在X与y相关矩阵中提取第一主成分t1，利用y和X对t1进行回归，t1要求携带X矩阵中的大量变异信息，并与y的相关性最大。这就要求有个能够度量x信息，又能最好地解释Y的准则。此时采用交叉有效性原则，度量因子：

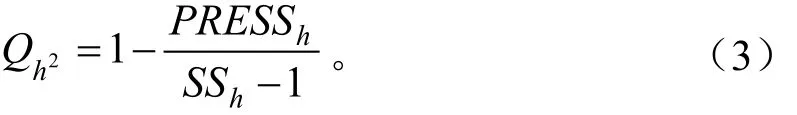
3.1 回归建模步骤

3.1.1 数据标准化处理

自变量数据是不同性质指标，直接加总不能反映不同作用力的综合作用，且数据处理复杂，需对其进行如下标准化以消除不同量纲的影响。

式（4）与式（5）中，F0，E0分别为Y，X的标准化矩阵，E(y)，E(xi)分别为Y，X的均值，Sy，Sxi分别为Y，X的均方差，n为样本容量。

3.1.2 主成分提取

从Zx中提取第一主成分，t1=Zx×W1，W1为Zx第一主成分对应的特征向量。同时，从Zy中提取第一主成分产u1-Zy×C1，C1为Zy第一主成分的特征向量。根据偏最小二乘思想，要求t1、u1能很好代表X、Y变异信息，并且要t1对u1最大解释能力，实际就是求t1与u1协方差最大。得到：

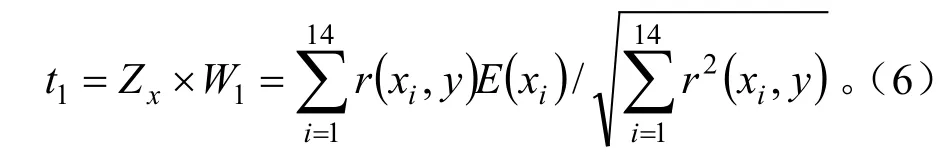
式（6）中：r(xi，y)表示xi与y的相关系数。从t1的达式可看出，t1不仅与X有关，而且与y有关。求得第一主成分t1后，分别求Zx与Zy对t1的回归方程，再利用两回归方程的残差矩阵设为A、B，进行第二主成分的提取。

同时根据度量因子公式计算Qh2为0.237 9大于0.097 5，因此根据第二主成分提取的方法继续第三主成分提取，并计算Qh2为-0.093 2小于0.097 5，因此终止主成分的提取。得到的3个主成分与Zy回归方程为：

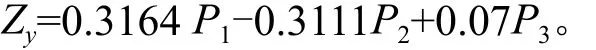
还原为原始变量偏最小二乘方程为：

Y=54.718 8+5.619 9× 郁 闭 度 +0.030 6 × 坡度 +0.000 7× 海 拔 -38.190 1×TM1-4.951 1×TM2+19.355 6×TM3+0.7837×TM4-2.048 ×TM5+5.552 9×TM7-0.569 5×NDVI-0.125× 比 值 +0.016 8TM(4+5-2)/(4+5+2)-0.751 3×亮度+13.358 5×绿度。

3.2 模型检验

为了对该模型的适用性进行有效的验证。本次研究将预留的30个检验样本代入预测模型进行配对样本T检验，以便对实测蓄积量数据和模型预测值之间是否存在显著性差异作出评价，从而对反演模型的适用性进行检验，结果见表2。

表2 配对样本统计量及相关系数Table 2 Statistics and correlations paired samples

从配对统计量中看出，样本配对相关系数0.766，P=0.000＜0.05，因此认为两配对相关性显著。

对所建立的模型进行精度验证：

精度=1-（实测值-估测值）/实测值。

通过对30个样地模型的预测值与实测值的精度分析比较，得到30个样地蓄积量实测值为90.942 m3，模型预测值为81.95 m3，精度为90.1%。所建立的模型在适用性与精度上都满足要求，因此，所建立的模型可行。将通过样本配对检验与精度检验的模型反演到整个区域，在ERDAS的Model Maker里对自变量图层进行偏最小二乘模型运算，图层中的每一个像元值就变成了森林蓄积量值。根据像元统计信息得到研究区森林蓄积量估测值为2 447 695.203 m3，与密云县2006年一类清查的实测数据，220 万m3相比，精度达到为89.2%。在Arcmap里根据蓄积量估测图层生成蓄积量等级分布图如下：

4 结论与讨论

本研究以北京市密云县为对象，将研究区遥感图像、DEM模型结合样地调查数据，建立密云县森林蓄积量遥感估测模型，实现该区域森林蓄积量估测。主要结论如下：

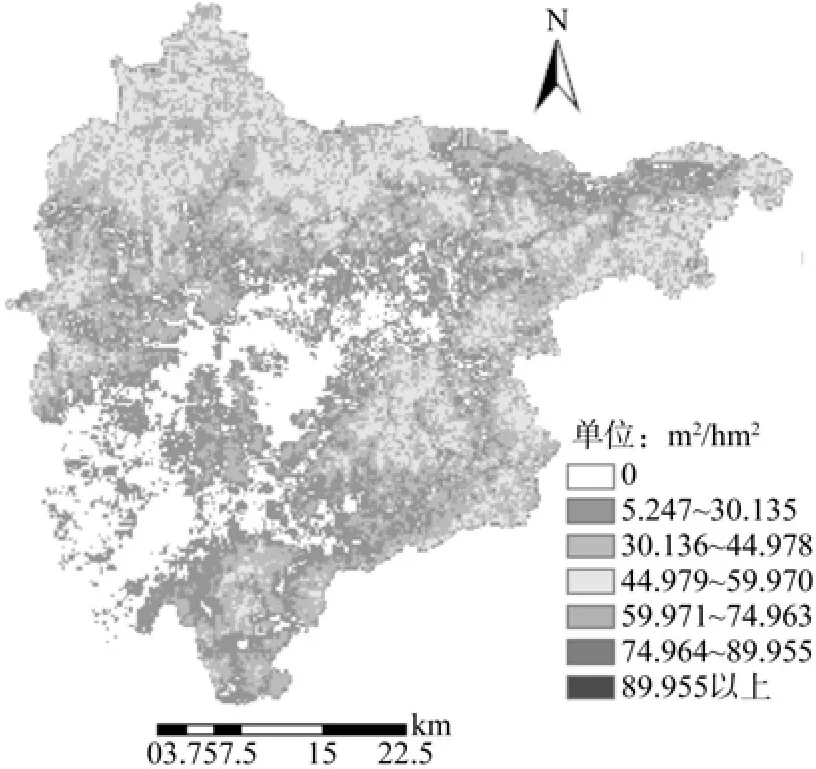
图1 密云县森林蓄积量等级分布Fig.1 Grade distribution of forest stock volume of Miyun County

（1）通过对遥感因子、地形因子与蓄积量进行相关性分析，选取了相关性好同时对模型显著性好的14个因子作为自变量建立森林蓄积量估测的偏最小二乘模型，用预留样本对其进行样本配对与精度检验，得到实测值与预测值存在显著相关性，精度达到90.1%。利用偏最小二乘既能解决自变量多重相关性问题，还能提取出对因变量解释高的信息，是一种集主成分分析与典型相关分析于一体的建模方法；

（2）将通过检验的模型反演到整个研究区，得到森林蓄积量估测值为2 447 695.203 m3，精度达到为89.2%。

结合TM影像和森林资源一类调查数据，利用偏最小二乘回归估测区域尺度上的森林蓄积量能获得较好的预测结果，也进一步验证了结合森林资源调查样地资料，开展全国范围的蓄积量估算，快速准确的进行森林生物量的动态监测和定量评价是一种行之有效的方法。

[1] 黄 平,杨燕琼,侯长谋.基于RS、GIS的杉木林分蓄积量判读模型研究[J].中南林业调查规划,2003,22(1):25-27.

[2] Tomppo E, Nilsson M, Rosengren M,et al.Sin ultaneous use of Landsat-TM and IRS-1CWiFS data in estimating large area tree stem volume and aboveground biomass[J]. Remote Sensing of Environment, 2002,82(1):156-171.

[3] 王臣立,牛 铮,郭治兴.基于植被指数和神经网络的热带人工林地上蓄积量遥感估测[J].生态环境学报,2009,18 (5):1830-1834.

[4] 万绍平.毛竹密度效应新模型的研究[J].经济林研究,1999,17(4):1-4.

[5] 李崇贵,赵宪文,李春干.森林蓄积量遥感估测理论与实现[M].北京:科学出版社,2006.

[6] 王松桂,陈 敏,陈立萍.线性统计模型线性回归与方差分析[M].北京:高等教育出版社,1999.

[7] 程武学,杨存建,周介铭,等.森林蓄积量遥感定量估测研究综述[J].安徽农业科学, 2009,37(16):7746-7750.

[8] 高惠璇.处理多元线性回归中自变量共线性的几种方法[J].数理统计与管理,2000,20(5):49-55.

[9] 涂云燕,彭道黎.基于神经网络的森林蓄积量估测[J].中南林业科技大学学报.2012,32(3):49-52.

[10] 韦玉春,黄家柱. Landsat5图像的增益、偏置取值及其对行星反射率计算分析[J].地球信息科学,2006,(1):110-113.

[11] Chander G, B L Markham. Revised Landsat-5 TM Radiometric Calibration Procedures and Post-Calibration Dynamic Ranges.Ieee Transactions on Geoscience and Remote Sensing, 2003,41(11): 2674-2677.

[12] 陈 楚,关泽群,张鹏林,等.利用RS和GIS的森林蓄积量偏最小二乘估测研究[J].湖北林业科技,2004,(4):25-28.

[13] 刘海清.森林蓄积量遥感估测的应用研宂[D].西安:西安科技大学,2009.

[14] 涂云燕,彭道黎.基于RS的森林蓄积量主成分回归估测[J].东北林业大学学报,2012,(10):75-77.

[15] 邓白罗.厚朴生长与立地因子关系的调查研究[J].经济林研究, 1994,12(1),41-46.

[16] 张正健,刘志红,郭艳芬,等.偏最小二乘在遥感监测西藏草地生物量上的应用[J].草地学报2009,17(6):735-739.

[17] 吴开亚,王玲杰.生态足迹及其影响因子的偏最小二乘回归模型与应用[J].资源科学,2006,28(6):182-188

[18] 杜晓明,蔡体久,琚存勇.采用偏最小二乘回归方法估测森林郁闭度[J].应用生态学报,2008,19(2):273-277.

[19] 洪奕丰,林 辉,等.基于偏最小二乘的平南县森林蓄积量估测模型研究[J].中南林业科技大学,2011,31(7):80-85.

Estimation of forest stock volume based on partial least squares regression

LIU Qiong-ge , PENG Dao-li , TU Yun-yan
(College of Forestry, Beijing Forestry University, Beijing 100083, China)

Forest stock volume is affected by remote sensing factors and topographical factors, but there is a multiple correlation between the factors that can affect the stability of the model and the accuracy of prediction. Aiming at the problem of multiple correlation between the estimation independent variables, the partial least squares regression was adopted and the remote sensing estimation of forest volume model for Miyun county of Beijing which differs from the traditional least squares method was established. The factors that may affect the stock volume were found out and the factors related with stock volume and signif i cantly inf l uenced to model were selected as independent variables of forest stock volume estimation model. The model was examined by the sample reserved, and the predicted values were compared with the measured values, the accuracy of the set aside sample was 90.1%. By using the tested model to predict forest stock volume, the estimated value of forest stock volume for Miyun county was 244 769 5.203 m3.

forest stock volume; remote sensing factors; topographical factors; multiple correlations; partial least squares

S757.2+19

A

1673-923X(2014)02-0081-04

2013-05-02

中国森林植被调查（2013FY111600-1）；“十二五”农村领域国家科技计划课题“数字化森林资源监测关键技术研究-森林结构参数反演技术研究”（2012AA102001-5）；国家级林业推广项目（201145）

刘琼阁（1987-），女，河南郑州人，硕士研究生，主要从事森林资源监测与评价研究；E-mail：qionggeliu@126.com

彭道黎（1963-），男，湖南常德人，教授，博士生导师，主要从事森林资源监测与评价研究；E-mail：dlpeng@bjfu.edu.cn

[本文编校：文凤鸣]