昆明典型地表死可燃物含水率预测模型的研究

金 森，周 勇

（东北林业大学 林学院，黑龙江 哈尔滨 150040）

昆明典型地表死可燃物含水率预测模型的研究

金 森，周 勇

（东北林业大学 林学院，黑龙江 哈尔滨 150040）

云南省是我国重点火险区，准确预测该省可燃物含水率对于提高火险预报准确性十分必要。在2013年防火期，通过对昆明地区8个林分地表凋落物可燃物含水率的连续观测，分析了其动态变化规律和影响因子，并采用气象要素回归法、FWI法和两种方法混合建立了相应的死可燃物含水率预测模型。这些模型采用的预报因子都是现有常规气象站方便观测的气象要素，模型误差在同类研究的控制水平内，可以在该地区的森林火险预报中直接应用。对于＜35%的可燃物含水率的预测，采用混合模型的误差最小，考虑到计算的方便，实际中可以使用气象要素回归模型，平均绝对误差（MAE）2.1%～6.0%，平均3.6%；平均相对误差（MRE）11.4%～32.7%，平均21.3%。如果考虑降雨后的可燃物含水率，即全部范围的可燃物含水率的预测，三种模型没有显著差异，为计算方便，仍建议采用气象要素回归模型，MAE 8.2%～14.2%，平均10.6%；MRE 48.7%～91.3%，平均值61.4%。FWI指标与地表死可燃物含水率有关，但不如气象要素那么紧密。

林分地表死可燃物；含水率； Fire Weather Index(FWI) ; 模型；昆明

森林可燃物是森林燃烧的物质基础，地表死可燃物含水率直接影响森林燃烧的难易程度和林火行为[1-3]。对死可燃物含水率的预测，是做好火险天气预报和火行为预报的关键[4-13]。云南省地形地势复杂、可燃物类型多样、森林小气候差别大，这些与当地生产生活用火的多样性和复杂性，造成了云南省林火行为的复杂性和森林防火任务的艰巨性。建立该省准确的森林可燃物含水率预测模型十分必要。李世友、舒清态等[14-15]建立了包含调落物层地表温度、腐殖质层表面温度等为预测因子的云南松和华山松林地表可燃物无降雨条件下的含水率线性预测模型，具有较好的精度。但凋落物层地表温度、腐殖质层表面温度不是气象站的常规观测因子，一般不易得到数据，限制了这些模型的应用。而且，该模型针对没有降雨时的可燃物含水率，没有考虑降雨的影响，从含水率范围上看不完善。另，云南森林类型众多，这些研究只研究了两个最重要的林分类型，其他一些比较重要的林分的可燃物含水率还没有研究，而可燃物含水率受林分类型影响强烈，应针对这些类型分别建立含水率预测模型。因此，对于云南省，针对更多林型的，建立以容易测定的气象站常规观测因子为预测变量，考虑降雨、覆盖更宽含水率幅度的地表可燃物含水率预测模型十分必要。

为此，我们以昆明市多个典型林分的地表死可燃物为研究对象，研究了用气象站常规观测因子，包括降雨，来预测更大范围的地表死可燃物含水率的方法和模型。方法上主要选择易于应用且有一定精度的气象要素回归法和时滞平衡含水率法[16]。其中时滞和平衡含水率法采用加拿大系统的森林火险天气指标系统（FWI）[17]。通过本研究，一方面建立该区域的适用的可燃物含水率预测模型并分析这些方法的误差情况，另一方面来评价FWI指标在昆明地区的适用性[18-23]。

1 研究方法

1.1 研究地区介绍

研究地区位于昆明市大凹子村 (25°05′55″N，102°50′3″E)。昆明地处云贵高原中部，海拔高度1891m，三面环山，南临滇池，四季如春，干湿季分明，属低纬高原山地季风气候。全年晴天较多，日照数年均2 445.6 h，日照率56%，紫外线强，全年降水量约1 031 mm，相对湿度为74%，全年无霜期在240 d以上，加之雨量适中，土壤较肥沃，地下水位较高，有利于大多数植物生长。常见的乔木树种有：华山松Pinus armandi、云南松Pinus yunnanensis、圆柏Sabina chinensis侧柏Biota orientalis等。灌木主要有：云南杨梅Myrica nana A.Cheval、滇南杜鹃（Rhododendron hancockii Hemsl、南天竹Nandiana domestica等。草本主要有：车前草Plantagoasiatica L、十字马唐Digitaria cruciata、过路黄Lysimachia christinae Hance和路边青Geum aleppicum Jacq等。

1.2 野外试验

1.2.1 样地设置

选取云南松林、华山松林和圆柏林的不同坡向、坡位样地，共8块。其中华山松3块，云南松纯林1块，云南松混交林3块，圆柏林1块。同一树种的林分选择多个样地是为了便于分析郁闭度等林分特征对可燃物含水率的影响。在每个林分内设立20 m×20 m的样地，做常规调查。样地信息参见表1。

1.2.2 野外试验

在2013年2月27日～5月31日（共94天，昆明的防火期），每日13时左右在每块样地取地表凋落物4份，每份50 g左右，称鲜重后装入密封袋，带回室内入烘箱内105℃连续烘干24 h至绝干，记录绝干质量。

在云南松样地内设置一个HOBO自动气象站，每隔30 min采集一次空气温度、空气湿度、风速、降雨量。

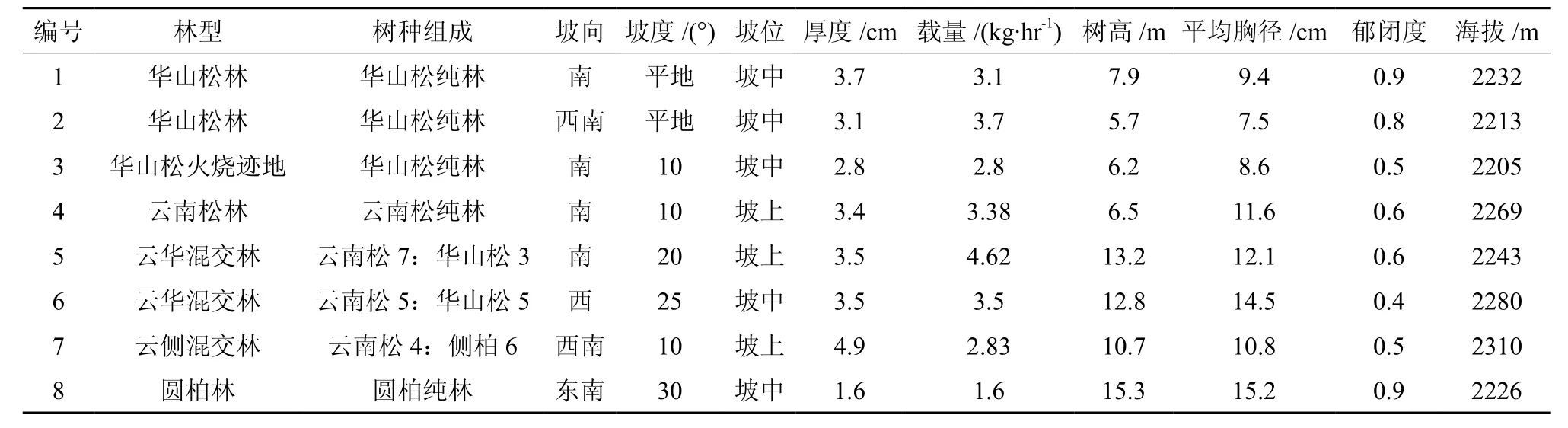
表1 样地信息Table1 Characteristic information of sample plots

1.3 数据处理和分析

1.3.1 死可燃物含水率计算与统计

按下式计算可燃物含水率含水率：

式中：M为物种死可燃物含水率(%)；Fm和Dm分别为物种的鲜质量(g)和干质量(g)。取4个样本含水率的平均值作为该调落叶含水率的实测值。

纤维的饱和含水率一般为35%，超过35%的可燃物床层出现自由水，受降雨和凝露等影响。且一般可燃物的灭绝含水率在35%[24]。所以将含水率数据分为小于35%和全部含水率数据两类。进行基本统计分析，给出统计特征。

1.3.2 FWI指标的计算

FWI系统有6个输出参数：细小可燃物湿度码(FFMC)、半腐层湿度码(DMC)、干旱码(DC)、初始蔓延速度(ISI)、可燃物累积指数(BUI)、火险天气指数(FWI)。这些指标按文献计算[17]。FFMC、DMC和DC的初始值按冬季没有显著积雪覆盖的地区计，即当连续3天的日平均气温达到或超过6℃后开始计算，FFMC=85，DMC为上次降水到现在的日数的2倍，DC值为上次降水到现在的日数的5倍。因此，本研究FFMC、DMC和DC的初始值分别为85、90和225。

1.3.3 可燃物含水率影响因子分析

对可燃物含水率有影响的因子有两类：一是气象因子，包括当日和前一、二日的日最高气温（℃）、日平均气温（℃）、13时温度（℃）、日平均湿度（%）、风速（m·s-1）、降雨量（mm），二是FWI系统的六个指标。温度记为TM-X，相对湿度H-X，平均风速W-X，降雨量R-X。各变量下标中：M为MAX、A或13，分别表示最高、平均和13时；X为0、1和2，分别表示当日和前一、二日。前2、5和10天的降雨量总和（mm），分别记为R2、R5和R10；最近一次降雨量（mm），记为R；连旱天数（day），记为D。分别以＜35%含水率和全部含水率数据，计算可燃物含水率与这些因子之间的Pearson相关系数，从而分析各因子对死可燃物含水率的影响。显著水平设定为0.05。

1.3.4 可燃物含水率预测模型的建立

对于每一个林分的可燃物，将两类含水率数据分别按4∶1的比例随机分为两组，其中较多的一组数据用来建立模型。利用SPSS软件，分别以气象因子、FWI6个指标和混合因子（气象因子+FWI指标）为预测变量，采用逐步回归的方法[25]建立该林分的地表死可燃物含水率三种多元线性预测模型，分别称为气象要素回归模型、FWI模型和混合模型。共建2×3×8=48个模型。用较少的一组数据验证模型，按下式计算平均绝对误差(MAE)和平均相对误差(MRE)，并做出实测值与预测值的对比散点图。用t检验比较三类模型间的预测误差差异显著性。

式中：Xi、Xj分别为死可燃物含水率的实测值和预测值，%；n为验证数据样本数。

2 结果与分析

2.1 可燃物含水率、气象因子和FWI湿度码的统计特征

表2给出了研究期间地表死可燃物含水率、气象要素和FWI三个湿度码的统计特征。可燃物含水率从5.8%到144.4%。25%和75%的分位数反映了研究地区可燃物含水率在防火期内多数比较干燥，从25%的分数位上看，有1/4的时候很干燥，低于11.0%。气象要素和湿度码也反映了研究地区的典型天气条件。

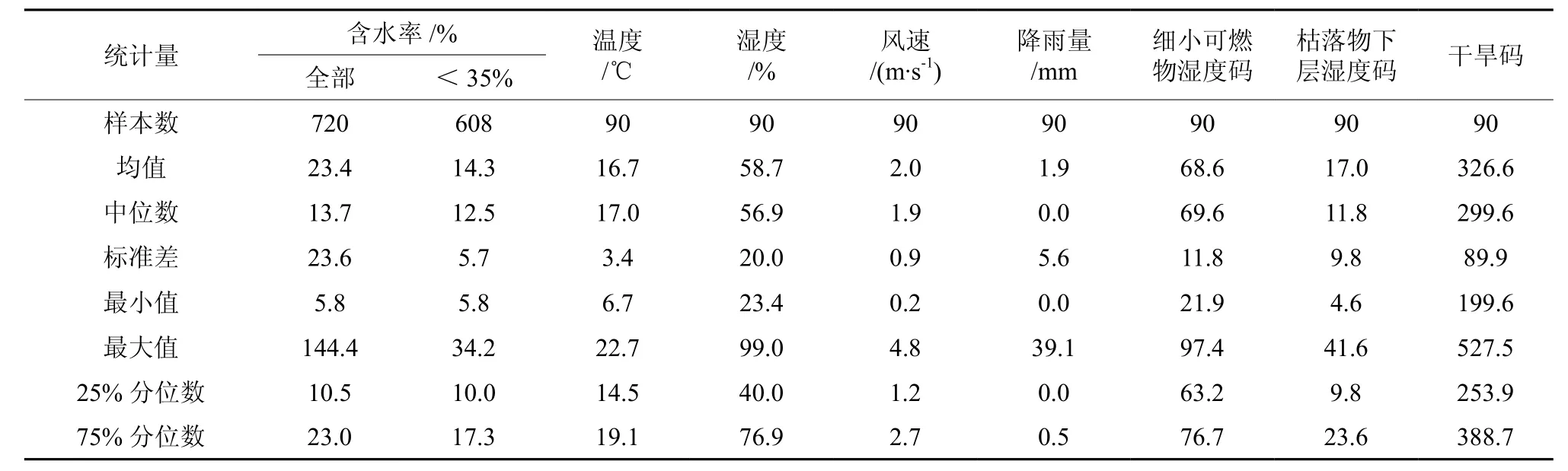
表2 可燃物含水率、气象要素和FWI湿度码的统计特征Table2 Statistics features of fuel moisture content, meteorological elements and FWI moisture codes

2.2 地表死可燃物含水率的影响因子

表3、4分别给出了不同含水率情况下，地表死可燃物含水率与影响因子之间的Pearson相关系数。表中所列出的影响因子，至少与一种死可燃物含水率相关，与所有死可燃物含水率均不相关的，未列入表中。

表3 死可燃物含水率（＜35%）FWI输出因子和气象因子的Pearson相关系数Table3 Pearson correlation coefficients for FWI output factors and meteorological factors of dead fuel moisture content (＜35%)

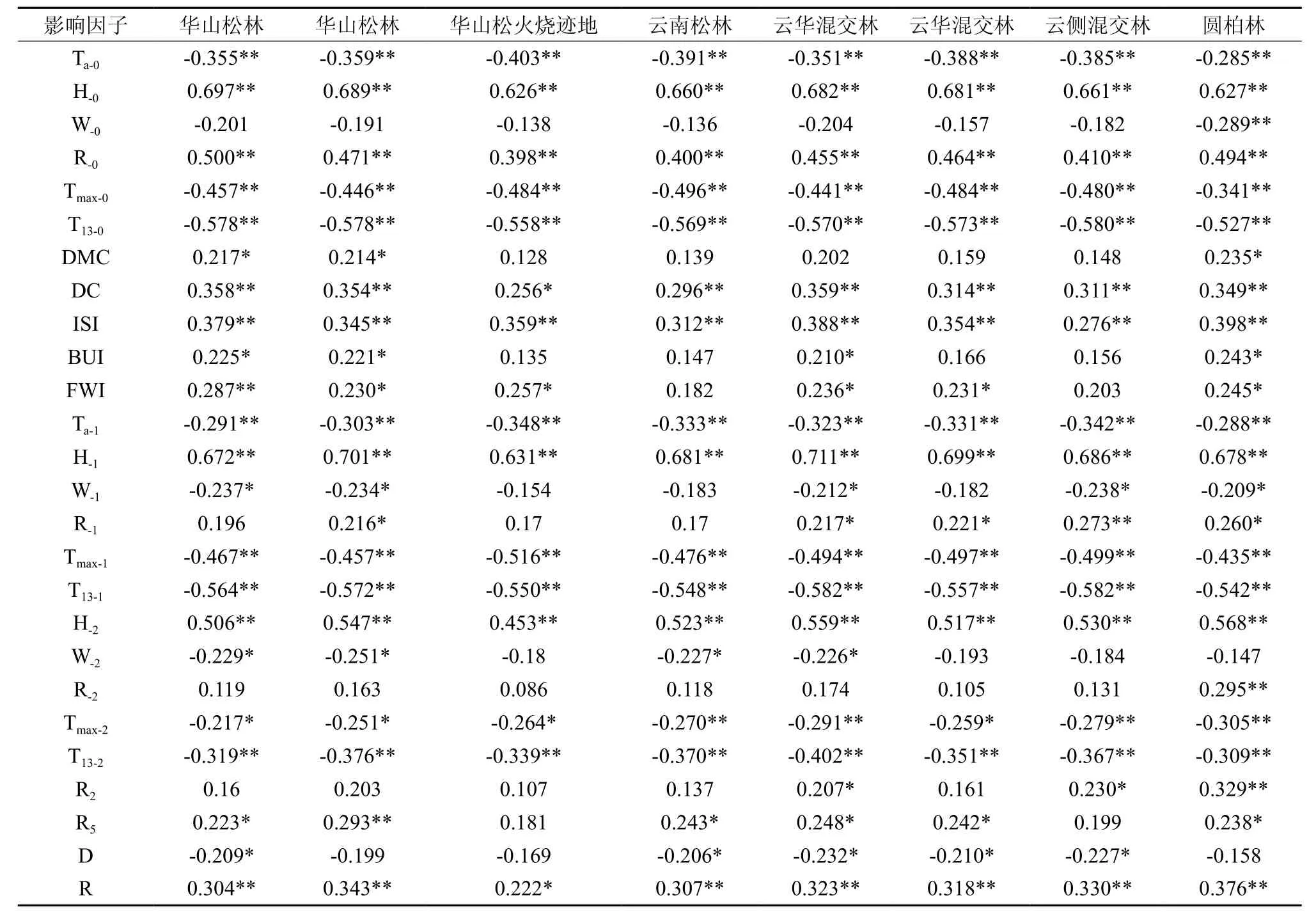
表4 全部死可燃物含水率FWI输出因子和气象因子的Pearson相关系数Table4 Pearson correlation coefficients for FWI output factors and meteorological factors of all dead fine fuel moisture content

当含水率小于35%时，与8个林分的死可燃物含水率都显著相关的变量有当日、前一、和二日平均湿度、13时温度、最高温度和前5天降雨量，与多数（5～7个）林分可燃物含水率显著相关的有ISI、DC、FWI、当日降雨量、最近一次降雨量、当日平均温度和平均风速，与较少（3～4个）林分可燃物含水率相关的有前一日最高温度和前2、10天降雨量和；而DMC、BUI、前一日降雨量和连旱天数仅与个别（1～2个）林分的可燃物含水率相关。对于全部含水率数据，与全部死可燃物类型显著相关的有当日和前一日的平均湿度、当日和前一日、前二日的平均温度、最高温度、13时温度，降雨量，干旱码。其中前二日平均湿度、当日降雨量当日和前一日13时温度和最高温度与全部可燃物类型最为紧密。

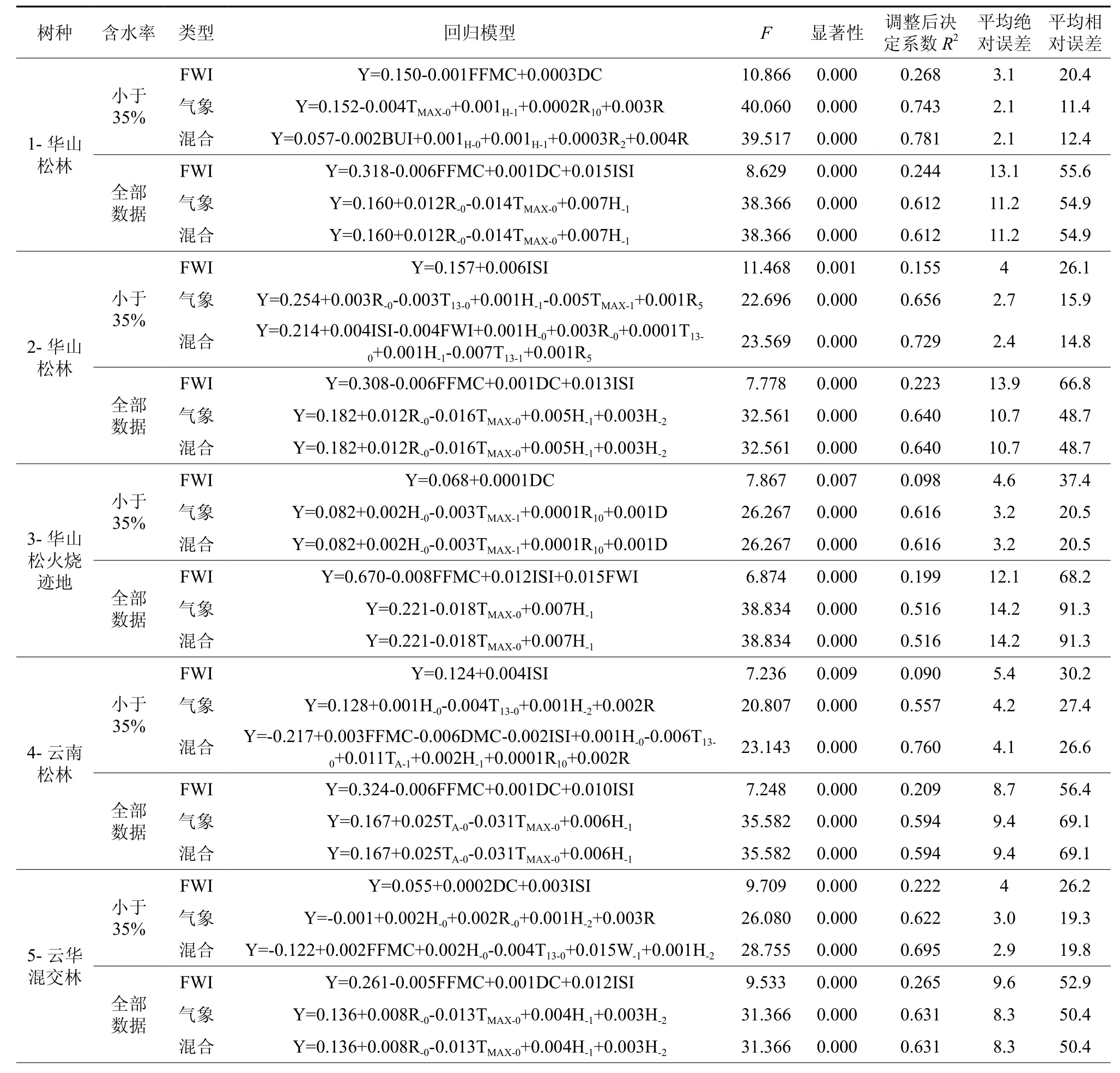
表5 地表死可燃物含水率预测模型的参数和检验Table5 Parameters and statistical test of prediction models established using moisture content of forest combustible

2.3 地表死可燃物含水率预测模型及比较

表5给出了8个不同林分情况下地表死可燃物含水率预测模型的参数和检验。在含水率小于35%和全部含水率情况下，所有预测模型均显著，说明模型可用。

对于三种模型，FWI模型使用最多的变量是FFMC、DC和ISI，16个模型中分别使用了10、12和13次；气象要素回归模型使用最多的变量是当日和前一日平均湿度，16个模型分别使用9和11次，其次是当日降雨量和最高温度，各使用7次；混合模型中使用最多的是当日和前一日平均湿度，均为12次，其次为当日降雨量和当日最高温度，均为8次，再次为最近一次降雨量，为6次。其它因子在预测模型中出现次数相对较少。表3和4中其它与可燃物含水率密切相关的因子没有出现在模型中是因为这些因子与进入模型的因子具有一定的相关性，其对含水率的作用通过进入模型的因子所体现。

续表 5The contiuation of table 5

含水率小于35%时，FWI预测模型可解释9%-26.8%的可燃物含水率变差，模型虽然显著，但解释变差相对弱一些。其MAE为3.1%-5.4%，平均4.5%；MRE 20.4%～37.4%，平均28.0%。气象要素回归模型可解释53.7%～79.8%的可燃物含水率变差，MAE 2.1%～6.0%，平均3.6%；MRE 11.4%～32.7%，平均值21.3%。混合预测模型可解释53.7%～87.2%的含水率变差，MAE2.1%～5.9%，平均3.5%；MRE 12.4%～29.6%，平均20.4%。

全部含水率时，FWI预测模型可解释16.8%～26.5%的可燃物含水率变差，其MAE为8.7%～15.1%，平均11.6%；MRE 52.6%～81.8%，平均63.3%。气象要素回归模型可解释51.6%～67.2%的可燃物含水率变差，MAE 8.2%～14.2%，平均10.6%；MRE 48.7%～91.3%，平均值61.4%。混合预测模型可解释51.6%～68.6%的含水率变差，MAE7.9%～14.2%，平均10.3%；MRE 48.7%～91.3%，平均59.7%。

表6给出了在不同含水率情况下对三类建模的误差差异显著性的t检验结果。从中可见，在含水率小于35%时，除气象要素回归模型与混合模型的MRE差异不显著外，三个模型的误差都显著差异，FWI模型误差最大，其次是气象模型，混合模型最小。8个混合模型中，3个模型与气象模型一样，没有任何FWI因子加入，其他5个有FWI指标加入的混合模型，其MAE于气象模型相比，改进的很小。这表明，对于＜35%的含水率预测，增加FWI指标虽然能够改进部分林分可燃物含水率的预测精度，但十分有限。对于可燃物全部含水率而言，三类模型的两类误差差异都不显著，其中FWI和混合模型接近差异显著。这说明，对于由降雨影响的含水率预测，三种方法没有实质的区别。

图1和2分别给出了所有含水率小于35%数据和所有含水率数据三种建模的预测实测值对比情况。由图1可见，FWI模型以15%含水率为临界，低于临界时对含水率预测偏高，高于临界时则含水率预测偏低，且预测结果误差很大。气象要素回归模型和混合模型的散点图分布上大致相同，这说明这两类模型的预测效果相近(一些林分的两类模型是一样的)，在含水率＜25%范围内，散点均匀地分布在直线两侧，预测效果较好，但通过散点到直线的截距来看，气象要素预测模型要优于混合预测模型。图2中直线为y=x，对于全部含水率数据，FWI模型预测低含水率是预测偏高，高含水率时预测偏低。气象要素回归模型同样，但高含水率阶段偏高和偏低比较均衡，表示模型的无偏性较好，而混合模型在高低含水率都具有较好的无偏性。

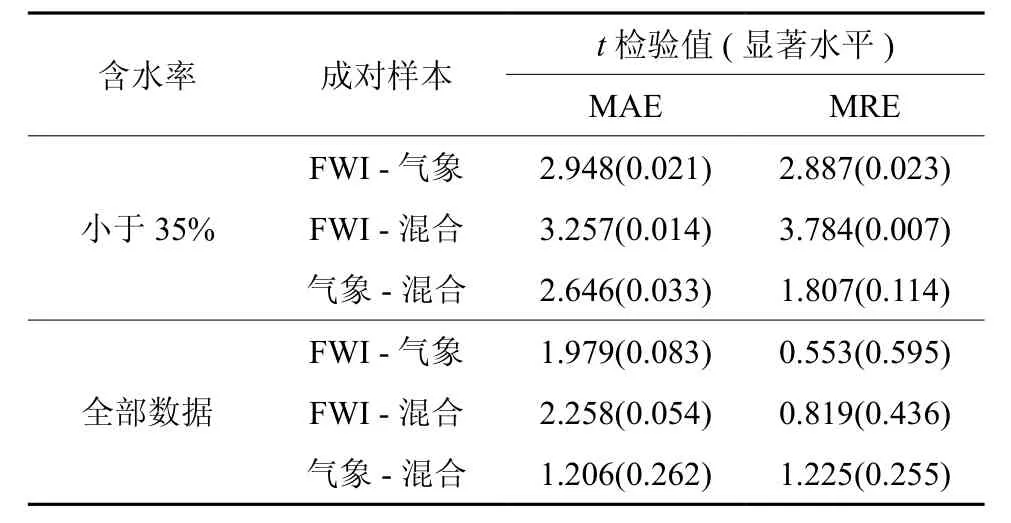
表6 两类含水率情况下三类预测模型成对样本的t检验Table6 T-test of paired samples of three kinds of prediction models of two kinds of moisture content

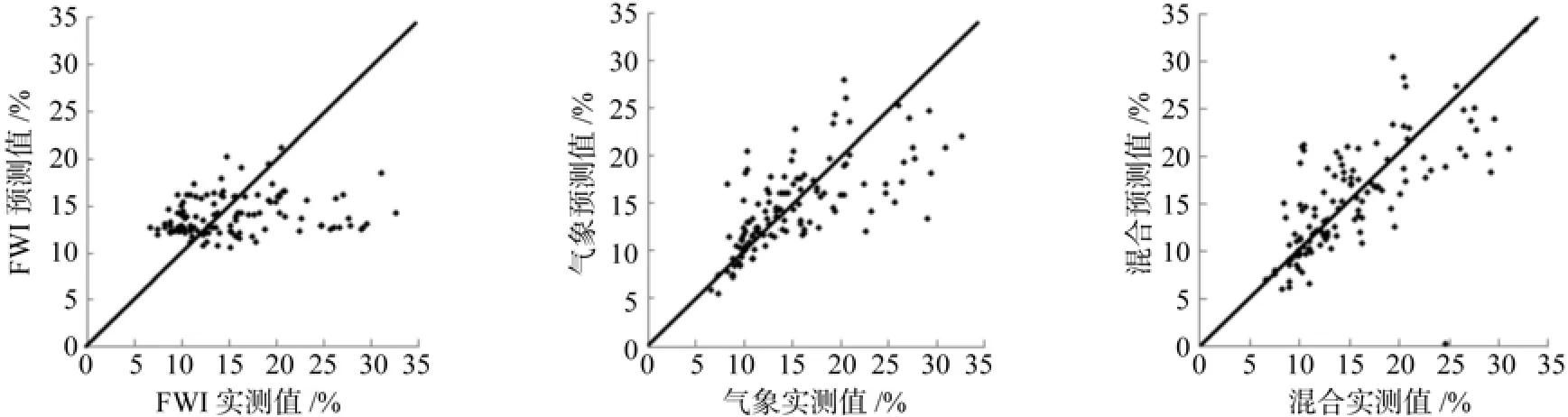
图1 所有含水率小于35%数据三种模型的预测实测值对比Fig.1 Comparisons of measured and computed fuel moisture values (＜35%) by three type models

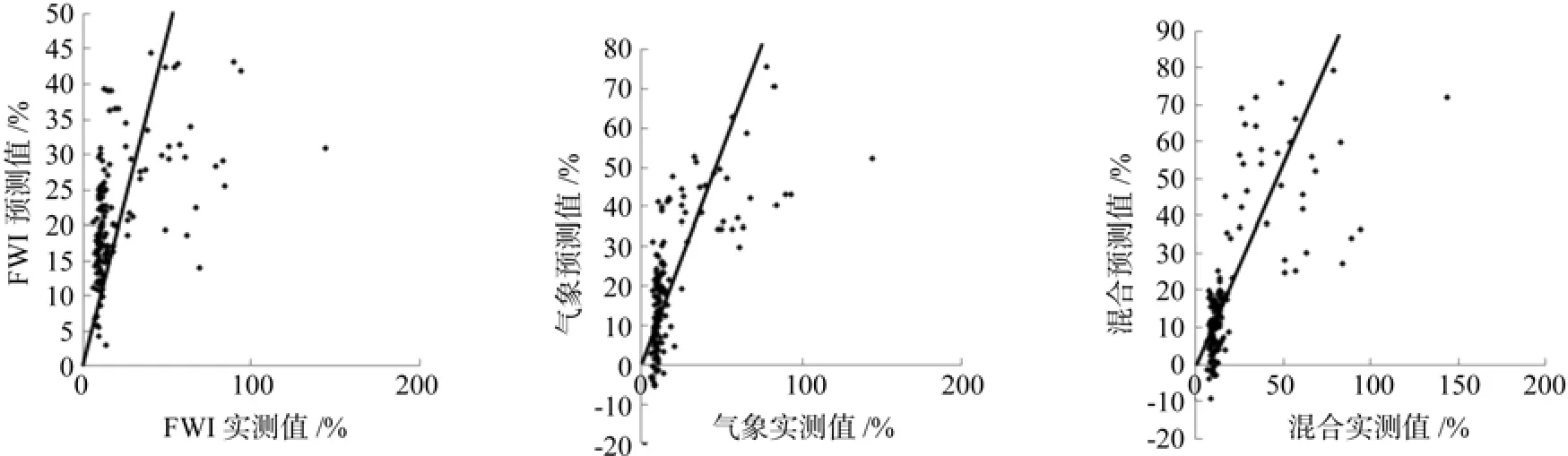
图2 全部含水率数据三种方法单独建模（交叉验证）的预测实测值对比Fig.2 Comparisons of measured and computed fuel moisture values (full moisture range) by three type models

3 结论与讨论

对昆明市典型可燃物含水率与气象要素等影响因子的逐步回归分析表明，对于＜35%的可燃物含水率的预测，采用混合模型的误差最小，但由于8个林分中3个林分的混合模型与气象模型一致，另外5个混合模型比气象模型误差没有改进很多（误差减少不超过0.2%），考虑到计算的方便，实际中可以使用气象要素回归模型，MAE 2.1%～6.0%，平均3.6%；MRE 11.4%～32.7%，平均值21.3%。如果考虑降雨后的可燃物含水率，即全部范围的可燃物含水率的预测，三种模型没有差异，为计算方便，仍建议采用气象要素回归模型，MAE 8.2%～14.2%，平均10.6%；MRE 48.7%～91.3%，平均值61.4%。

FWI系统的一些指标与云南典型地表死可燃物含水率相关，以这些指标建立的线性可燃物含水率回归模型有效，表明FWI系统适用于该地区可燃物含水率预测，但需要进行本文这样的线性修正。但对于＜35%的含水率预测，其效果不如更简单的气象要素模型，但对于全部范围的可燃物含水率预测而言，其效果虽与气象要素回归法差异不显著，但两者结合能够有限地改进预测精度。考虑计算的简单性，对于昆明市的可燃物，气象要素回归法优势最大。FWI方法虽然没有特别优势，但如果考虑建立与其他省区结构相似的可燃物预测模型，则FWI方法可作为一个选择。

李世友、舒清态[14-15]所建立的华山松林分可燃物含水率预测模型的平均MAE为2.0%，MRE平均8.1%，其云南松林分含水率模型的MAE均值3.5%；MRE均值14.3%。本文所建模型的误差高于他们。主要原因是他们的模型采用可燃物表面温度作为预测因子，能够更好地反应可燃物的干湿程度。本研究采用的是气象站温湿度，与可燃物表面温湿度有一定差异。如果将气象站温度和湿度转换成地表可燃物的温湿度，如Slijepcevic等[26]所做，可能提高模型的精度，但需要建立针对这些可燃物类型的专门的转换模型，这是今后应加强的工作。

本研究模型与文献中同类模型的误差具有一定的相似性。对于FWI模型，Simard等[27]用FWI预测凋落物含水率的误差为16.5%，Chrosciewicz[28]对FWI修正的模型误差为16-18%。本文中FWI模型的MAE平均11.6%，比这些模型还要低一些。对于气象要素回归模型，国内外很多气象要素回归模型没有直接给出误差，难以进行全面的比较。Ruiz等[29]建立的含水率＜30%的气象要素回归模型，其MAE为1.32%，本研究对于＜35%的气象要素回归模型的平均MAE为3.5%，高于该模型，可能的原因是前者的样本只有49个，含水率＜30%而不是35%，且模型参数多。

虽然本研究模型比该地区李世友、舒清态[14-15]所建立的模型的误差大一些，但本文模型采用的都是通过现有的常规气象站方便观测的气象要素，且其误差在同类研究的控制水平内，因此，可以在该地区的森林火险预报中直接应用。无降雨时，可采用＜35%含水率模型，有降雨时，则采用全部数据模型。

2.3 中进入模型的气象因子主要是温度和湿度，其次是降雨。风速没有显式地出现在模型中，表3和4中风速与＜35%的8个林分中的5个的可燃物含水率相关，但对于全部可燃物含水率，只有1个林分的含水率与之相关。这与其他研究的结果相似，风虽然对可燃物变干有影响，但林分内风速与气象站的风速有差异，且风速变化较大，因此，其对含水率的影响不如温湿度明显。

对于气象要素回归法，能够反映可燃物采样地微气象条件的气象数据是提高模型精度的关键。李世友、舒清态[14-15]模型的误差较小就是实证。Aguado等[30]指出，气象站数据的不足是产生误差的重要原因。气象站的所处位置与样地之间的距离远近、地形和林型的变化、树冠的遮挡程度，使气象站记录的数据与采集样地的实际情况有一定偏差，甚至出现气象站记录的降雨很大，但采样地受树冠遮阴等影响，部分样地的凋落物含水率增加不大，使得有降雨情况下的可燃物含水率预测误差增加，也是全部数据建模误差大的重要原因。对雨后可燃物含水率的动态变化应加强研究。

[1] 马丽华, 李兆山. 大兴安岭6种活森林可燃物含水率的测试与研究[J]. 吉林林学院学报, 1998, 14(1):21-23.

[2] Reifnyder W E. Seasonal variation in the moisture content of the green leaves of mountain laurel[J]. Forest Science,1961,7:16- 23.

[3] 徐丽华. 地被可燃物与林型火险等级划分[J]. 辽宁林业科技,2001, (6):3-6.

[4] 邸雪颖, 王宏良. 林火预测预报[M]. 哈尔滨: 东北林业大学出版社, 1993.

[5] Rothermel R C, Wilson R A, Morris G A, et al. 1986. Modeling moisture content of fine dead wildland fuels: input to the behave fire prediction system[N]. United States Department of Agriculture, Forest Service, Research Paper INT-359.Intermountain Research Station, Ogden, Utah, 61.

[6] 单延龙, 刘乃安, 胡海清, 等. 凉水自然保护区主要可燃物类型凋落物层的含水率[J]. 东北林业大学学报, 2005,33(5):41-43.

[7] 何忠秋, 张成钢, 牛永杰. 森林可燃物含水率研究综述[J].世界林业研究,1996,(5):26-29.

[8] Chuvieco E P, Aguado I P, Dimitrakopoulos A P. Conversion of fuel moisture content values to ignition potential for integrated fi re danger assessment[J].Canadian Journal of Forest Research,2004,34(11):2284-2293.

[9] Nelson R M. Prediction of diurnal change in 10-hour fuel moisture content[J]. Canadian Journal of Forest Research, 2000,30: 1071-1087.

[10] 蔡卫红,王晓红,于宏洲,等.基于Rothermel模型的可燃物参数对林火行为影响的计算机仿真[J].中南林业科技大学学报,2013,33(11):34-41.

[11] 王晓红,张吉利,金 森.林火蔓延模拟的研究进展[J].中南林业科技大学学报,2013,33(10):69-78.

[12] 贾鹏超,曲智林,马普龙. 基于时间序列分析的可燃物含水率预测模型[J].东北林业大学学报,2013,41(5):157-158.

[13] 孙 萍,李大伟. 10种国内森林火险计算方法的相似性研究[J].中南林业科技大学学报,2013,33(5):17-21.

[14] 李世友,舒清态,马爱丽,等.华山松人工林凋落物层细小可燃物含水率预测模型研究[J]. 林业资源管理,2009,(1):84-88.

[15] 李世友,舒清态,马爱丽,等.云南松林凋落物表层细小可燃物含水率预测模型研建[J].山东林业科技,2008,(6):25-27.

[16] 刘曦,金 森.平衡含水率法预测死可燃物含水率的研究进展[J].林业科学, 2007, 43(12):126-133.

[17] Van Wagner CE. Development and structure of the Canadian forest fi re weather index system[J]. Canadian Forestry Service,Technical Report, 1987,35-37.

[18] Wotton BK, Stocks BM, Martell DL. An index for tracking sheltered forest floor moisture within the Canadian Forest Fire Weather Index System[J]. International Journal of Wildland Fire,2005,14:169-182.

[19] 金继忠,韩树庭,周 薇.加拿大林火天气指标系统在大兴安岭林区的试[J].森林防火,1986,(3):20-24.

[20] Stocks B J, Lynham T J. Suitability of the Canadian Forest Fire Danger Rating System for use in the Daxinganling Forestry Management Bureau Heilongjiang Province, China[R]. Report to the Ontarion Ministry of Natural Resources, JIAPRO Study Group, 1986.

[22] 王会研,李 亮,刘 一,等. 加拿大火险天气指标系统在塔河林业局的适用性[J].东北林业大学学报, 2008,36(11):45-47.

[23] 王明玉.气候变化背景下中国林火响应特征及趋势[D].北京:中国林业科学研究院,2009.

[24] 田晓瑞, Douglas J. McRae,舒立福,等.大兴安岭地区森林火险变化及FWI适用性评估[J].林业科学,2010, 46(5)127-132.

[25] Rothermel R C.A Mathematical Model for Predicting Fire Spread in Wildland Fuels[J]. Washington DC:USDA Forest Service Research Paper,INT-115,1972(2).

[26] Komarek EV. Fire ecology: Grasslands and man[R]. Proceedings Fourth Annual Tall Timbers Fire Ecology Conference. Tall Timbers Research, Inc. Tallahassee, FL, 1965:169-220.

[27] Slijepcevic A, Anderson WR, Matthews S. Testing existing models for predicting hourly variation in fine fuel moisture in eucalypt forests[J]. Forest Ecology and Management, 2013,306:202-215.

[28] Albert J. Simard, James E. Eenigenburg, Richard W. Blank.Predicting fuel moisture in jack pine slash: a test of two systems[J]. Canadian Journal of Forest Research, 1984,14: 68-76.

[29] Z.Chrosciewicz. Prediction of forest-floor moisture content on jack pine cutovers[J]. Canadian Journal of Forest Research,1989,19: 239-243.

[30] Ruiz Gonza´lez AD, Vega Hidalgo JA, A´ lvarez Gonza´lez JG Construction of empirical models for predicting Pinus sp.dead fi ne fuel moisture in NW Spain. I. Response to changes in temperature and relative humidity[J]. International Journal of Wildland Fire, 2009,18, 71–83.

[31] Aguado I, Chuvieco E, Boren R Nieto H. Estimation of dead fuel moisture content from Meteorological data in Mediterranean areas. Applications in fire danger assessment[J]. International Journal of Wildland Fire, 2007,16:390-397.

Study on moisture content prediction model of dead surface fuels in typical stands, Kunming

JIN Sen, ZHOU Yong
(College of Forestry, Northeast Forestry University, Harbin 150040, Heilongjiang, China)

Yunnan Province is a high fi re risk region in China. It is necessary to accurately forecast fi re danger and improve the accuracy of fi re danger forecast. Successive observation of fuel moisture contents of dead surface fuels in 8 stands in Kunming, Yunnan province were conducted in 2013 forest fire prevention periods, the dynamics and affecting factors of fuel moisture content were analyzed.Moisture prediction models were established by using vapor exchange method, FWI method and method with mixed weather variables and FWI indexes. The predictors employed by the models all are the easily obtained weather variables from weather stations, and the models’ errors in the same control level within the have accuracy within the similar studies, and hence the models can be directly used application in forest fi re danger forecast in the area. For prediction of fuel moisture ＜35%, the vapor exchange models are the best choices, resulting minimal errors; By taking into account easy-to-calculate, in actual application, meteorological element regression models can be used, leading mean absolute error (MAE) 2.1%～6.0%, averaged 3.6%, leading the average relative error (MRE)11.4%～32.7%, an average of 21.3%. For predicting fuel moisture content after rain, no signif i cant difference existed among the three types of models. Considering easy computation, vapor exchange models are still the best choices with MAE 8.2%～14.2%, average 10.6%, and MRE 48.7%～ 91.3%，average 61.4%. FWI indexes are correlated with local fuel moisture but not as close as weather variables.

dead fi ne fuel on forest ground; water content; FWI; model; Kunming city

S762.3

A

1673-923X(2014)12-0007-09

2014-04-11

林业公益性行业科研专项（201204508）资助

金 森（1970-），男，教授，博士，主要从事森林防火研究；E-mail：jinsen2005@126.com

[本文编校：吴 彬]