高空作业车静液压调平系统的优化研究

谭苗苗

（北京联合大学机电学院，北京100020）

0 引言

高空作业装置广泛应用于建筑、消防等行业，其调平系统是保证设备安全可靠工作的核心技术之一［1］。目前常用的调平机构主要包括平行四连杆机构、静液压调平机构、电液调平机构、混合式调平机构等［2］。平行四连杆调平机构由一组或多组平行四边形连杆机构组成，调平过程是连续的，具有调平可靠、同步性好、机构简单的优点，但机构不够紧凑［3］。静液压调平原理是利用油液体积不变原理。由辅助油缸和调平油缸等组成一个封闭的自动调平回路。静液压式调平机构不受外部系统影响，结构简单，成本低，精度高［4-5］。

高空作业车的臂架在升降过程中，臂架和水平面必然会产生一定夹角，从而使工作斗以相同角度倾斜。调平机构需要实时快速对工作斗的倾角进行调整，否则将严重威胁高空作业人员的人身安全［6］。因此，如何优化调平系统的结构、减小误差、改善调平效果，从而可靠保证工作斗的水平姿态，对提高高空作业车的安全性和平稳性具有重要的研究意义。

调平机构优化设计的关键点在于确定优化目标、优化函数及约束条件。针对静液压调平机构，现有的优化研究均是针对特定的高空作业车型号，确定的优化目标和优化函数不同，对调平系统的优化效果有差异［7-9］。本文针对某型号高空作业车，选择的优化函数为Matlab优化工具中的fmincon函数，该函数适用于非线性规划优化方法。以工作斗连杆与水平面构成的夹角和水平参考点的最大偏差值为优化目标，将油缸的收拢长度与行程的差值作为约束条件之一，开展了对静液压调平机构的优化研究。通过对优化结果的仿真分析，证明该优化过程大大提高了调平系统工作的平稳性。

1 静液压调平系统分析

本文研究的高空作业车静液压调平机构如图1所示。静液压调平系统由基本臂、辅助油缸、调平油缸等组成。调平系统通过一个连杆机构与工作斗相连。高空作业车的基本臂在任何动作状态时，工作斗在调平系统作用下必须始终保持在水平姿态。静液压调平系统是通过辅助油缸和调平油缸的联动实现调平，即辅助油缸外伸时，调平油缸相应回收，从而实现工作斗的水平。

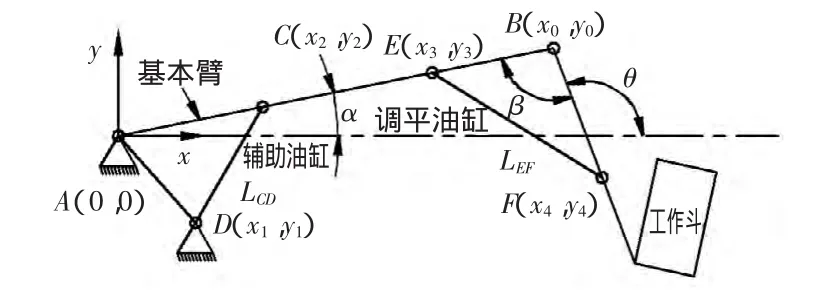
图1 高空作业车静液压调平系统示意图

以基本臂水平为初始状态定义坐标系。此时辅助油缸完全收拢，调平油缸完全伸出。基本臂回转点为原点A（0，0），基本臂的前支点坐标为 B（x0，y0）。基本臂转动角度为（0°<α<70°）。辅助油缸的两端点分别为 D（x1，y1），C（x2，y2）。调平油缸两端点分别为 E（x3，y3）和 F（x4，y4）。设辅助油缸两铰点距离为LCD，调平油缸两铰点距离为LEF。各变量初始值分别为：（x00，y00），（x10，y10），（x20，y20），（x30，y30），（x40，y40），LCD0，LEF0。当基本臂转动角度 α 时，各点值计算：

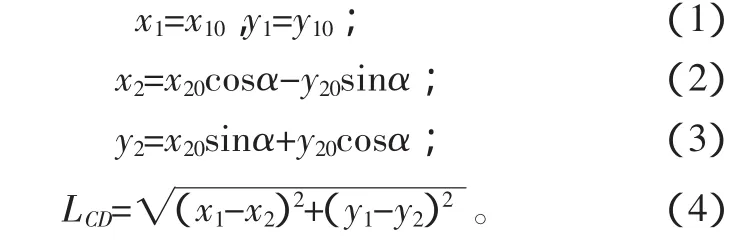
本系统中，辅助油缸伸出量与调平油缸回缩量相等，因此

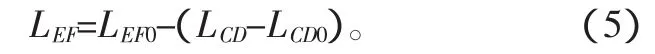
调平油缸、基本臂和连杆构成的三角形中，设LEF边的对角为β。由余弦定理：

设BF连线与水平线之间的夹角为θ。若基本臂转动任意角度α时，θ保持恒定不变，则工作斗可一直处于水平状态。由图1中的几何关系可知：

2 静液压调平系统铰点位置优化

结构优化的数学模型采用非线性规划模型，其数学形式为：

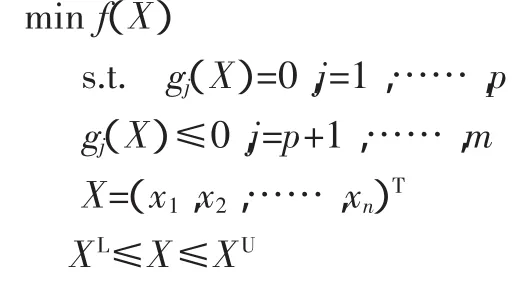
其中f（X）是目标函数，gj（X）为约束函数，X为设计变量，XU、XL分别为 X 上下限［10］。

2.1 优化变量

调平系统运行过程中，设定基本臂回转点A和前支点B为固定点。选择C、D、E、F四点坐标为优化点，即优化变量为 X=（x1，y1，x2，y2，x3，y3，x4，y4）T。

2.2 目标函数

设定在基本臂水平初始状态下，铰点BF连线与水平线之间的夹角为θ0。为保证工作斗在调平系统运行过程中始终水平，则基本臂在行程范围（0°<α<70°）内转动任意角度时，应保证BF连线与水平线之间的夹角θ与θ0之差Δθ的最大值尽量小，即工作斗与水平面的夹角相对初始水平状态的变化量最大值尽量小。因而优化设计目标是使 max（Δθ=θ-θ0）最小。即目标优化函数为：

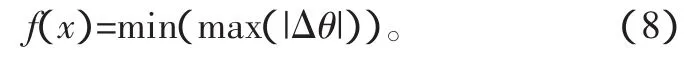
将式（6）代入式（7），则：

2.3 约束条件

静液压调平系统的辅助油缸和调平油缸运行过程中，油缸行程均需小于油缸的收拢长度。本文根据某型号高空作业车的实际工况，所设计油缸的收拢长度比油缸行程大250 mm以上。

根据系统初始状态定义，辅助油缸的收拢长度即为LCD0，行程为LCD-LCD0。则约束条件之一为：

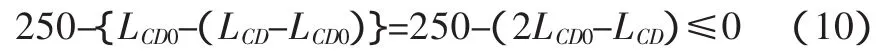
调平油缸的行程为LEF0～LEF，收拢长度为min（LEF）。当基本臂转动角度α达到行程范围的最大值70°时，调平油缸完全收拢，此时的LEF即为min（LEF）。则约束条件之二为：

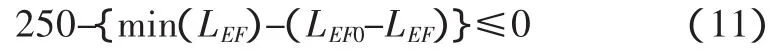
3 优化结果

根据本文所研究的高空作业车总体布局及基本臂转动角度范围（0°<α<70°），确定调平系统的各铰点参数及变化范围。其中固定点 B（x0，y0）的初始值为（7800，148）。

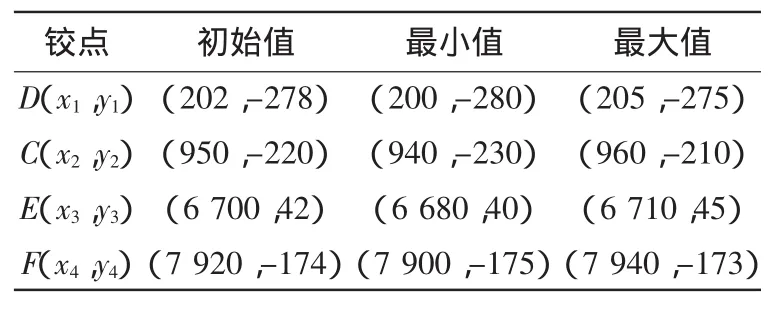
表1 高空作业车静液压调平机构的各铰点参数

本系统优化模型是一个有约束非线性规划的求最小值问题。采用Matlab中求解多变量有约束非线性函数极小值的函数fmincon进行优化。

变量优化结果为 X（202，-276.99，950，-220，6700，42.999，7920，-174），此时工作斗与水平面夹角相对初始状态的变化量Δθ的最大值为±0.1720°。考虑实际加工工艺的可行性，对优化变量进行圆整后的结果为X=（202，-277，950，-220，6700，43，7920，-174）T。此时，由式（1）～（7）计算得到 Δθ值的变化区间为（-0.1729°，0.1702°）。

优化设计前后的基本臂转动角度α与变化量Δθ关系曲线如图2所示。图中工作斗与水平面夹角的变化量Δθ越小，表明工作斗越接近水平平衡位置。由图可知，当基本臂转动角度小于20°时，Δθ值较小，且优化前后的Δθ值相近；当基本臂转动角度逐渐增加至40°时，Δθ值增大，且优化前后的Δθ最大值均不超过±0.2°；当基本臂转动角度再增加至最大角度70°过程中，优化前的Δθ值迅速增大，且在转动角度70°时达到最大值1.4°，而优化后的Δθ值正负波动变化，且最大值为0.1702°，为优化前Δθ最大值的1/10；基本臂转动角度在30°附近时，优化后的Δθ达到最大值-0.1729°。在本设计基本臂转动角度范围内，优化后的Δθ最大值与优化前相比显著减小。

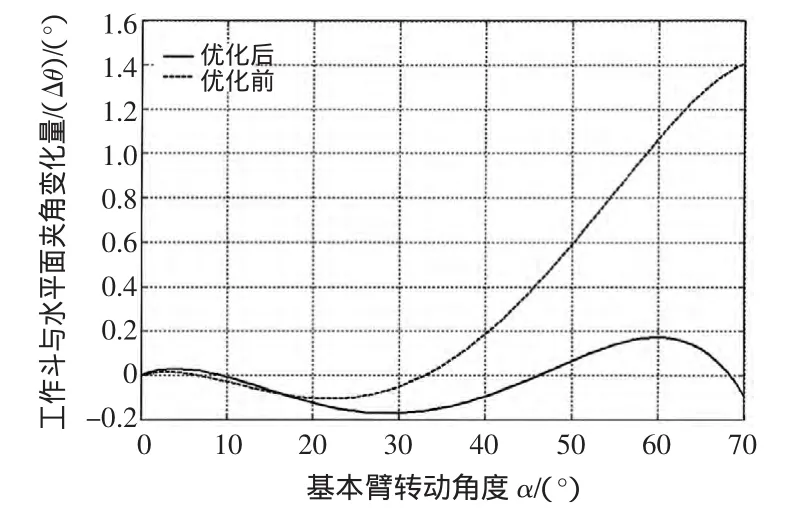
图2 优化前后工作斗水平状态与基本臂转动角度关系曲线

4 结论

本文针对高空作业车的静液压调平系统，应用最优化技术对静液压调平系统的各铰点位置进行了优化研究。以工作斗水平初始位置时，工作斗连杆与水平面的夹角为参考点，基本臂转动过程中，以工作斗连杆与水平面构成的夹角和参考点的最大偏差为优化目标，该最大偏差值越小表明工作斗越接近水平。通过仿真计算，优化后的偏差Δθ最大值为-0.1729°，是优化前偏差Δθ最大值1.4°的约1/10倍。该优化方法有效提高了调平系统工作的平稳性，可为静液压调平系统的设计开发提供数据支撑。

［1］ 黄桂芬，陈铭年.我国高空作业车研究进展综述［J］.机电技术，2012（1）：2-5.

［2］ 胡元.高空作业车工作平台调平机构［J］.工程机械，2006，37（7）：34-36.

［3］ 黄玲玲，曹希文.车载式高空作业车平台调平机构［J］.起重运输机械，2010（11）：80-82.

［4］ 於晓宇.液压连杆调平机构在绝缘高空作业车上的应用［J］.专用汽车，2012（8）：95-96.

［5］ 蔡雷.高空作业车结构分析及工作斗调平系统研究［D］.长春：吉林大学，2005.

［6］ 郭维城，张陈，肖楠.基于ADAMS的桅杆式高空作业车倾翻性研究［J］.机械设计与制造，2011（10）：266-268.

［7］ 李钦奉，江伟，张礼军.多功能高空作业平台伸缩臂的有限元分析与优化［J］.机械设计与制造，2012（5）：270-272

［8］ 王津.自行式高空作业车作业臂有限元分析与优化设计［D］.西安：长安大学，2009.

［9］ 张璐.基于安全的高空作业车的设计优化及可靠性研究［D］.秦皇岛：燕山大学，2009.

［10］ 许怡赦，施大发，郭雄华.伸缩臂叉车调平机构优化设计［J］.现代制造工程，2012（6）：60-63.