基于无偏灰色马尔可夫链的吉林省降水量预测

张 茜，梁秀娟，杜 川

吉林大学环境与资源学院 长春 130021

0 引言

降水量指从天空降落到地面上的液态或固态（经融化后）水未经蒸发、渗透、流失，而在水平面上积聚的深度。降雨经过下垫面的调蓄作用产生径流，降雨、径流是水资源循环中的两个核心环节，其大小直接影响农业灌溉、河道航运、水土保持等方面［1］。对于吉林省这样以农业为主产业的地区，准确的降水量预测是合理调整种植结构、提高产量、降低气象灾害的最佳途径。

国内外有很多关于降水量预测的方法：肖长来等［2］采用模糊均生函数残差模型对吉林省西部降水量进行了预报，数据证明这是一种理想而实用的方法；吴春勇等［3］采用频谱分析以及自回归模型对挠力河进行了降水量预报，该方法利用傅里叶函数展开理论建立模型，简单易懂、计算速度快、精度较高，但仍存在一定的缺点和不足，如傅里叶函数存在吉布斯效应，使时间序列在极值处拟合较差；夏乐天等［4］采用加权马尔可夫链对郑州市的降水状况进行了预报，但其仅能预测降雨的丰枯状态，不能计算准确数值；Vahid Nourani等［5］采用基于神经网络的小波分析法对Ligvanchai流域降水量进行预测，结果表明预测效果与时间序列长度有关，大样本容量会提高预报的准确性；李生彪［6］运用无偏灰色模糊马尔可夫链对甘肃省人均GDP进行了预测，其结果的准确性和合理性明显优于传统的灰色马尔可夫模型。

因历史资料所限，大多数研究者只对一个雨量站的降水情况进行了预测，而笔者选用了吉林省分布在各市8个雨量站的长系列资料，利用无偏灰色马尔可夫链的方法，不仅纵向地进行了降水量的预报，还将结果进行横向分析，得出全省的降水量时空分布变化特征，并且讨论历史数据波动性与预报精度的关系，目的是提高农业经济效益、提高水资源利用率、合理进行水资源调度。

1 研究区概况

吉林省位于中国东北中部，东经122°-131°、北纬41°-46°，面积18.74万km2。吉林省是河源省份，处于东北地区主要江河的上、中游地带，省内有5条河流（松花江、鸭绿江、图们江、辽河、绥芬河）直接入海；地貌形态差异明显，地势由东南向西北倾斜，呈现明显的东南高、西北低的特征；以中部大黑山为界，可分为东部山地和中西部平原两大地貌区；东部山地分为长白山中山低山区和低山丘陵区，中西部平原分为中部高平原区和西部低平原区。全省多年平均日照时数为2 259～3 016h，年平均降水量为400～600mm。

2 数据来源及研究方法

2.1 数据来源

笔者选取吉林省8个地级市具有代表性的雨量站，分别为白城市（白城站）、松原市（乾安站）、长春市（长春站）、吉林市（蛟河站）、延边自治州（延吉站）、四平市（四平站）、通化市（通化站）和白山市（靖宇站），各雨量站的分布位置如图1所示。数据为1957 -2010年平均降水量资料，其中1957 -2000年44a的时间序列为空间样本，2001 -2010年10 a的时间序列为检验样本。

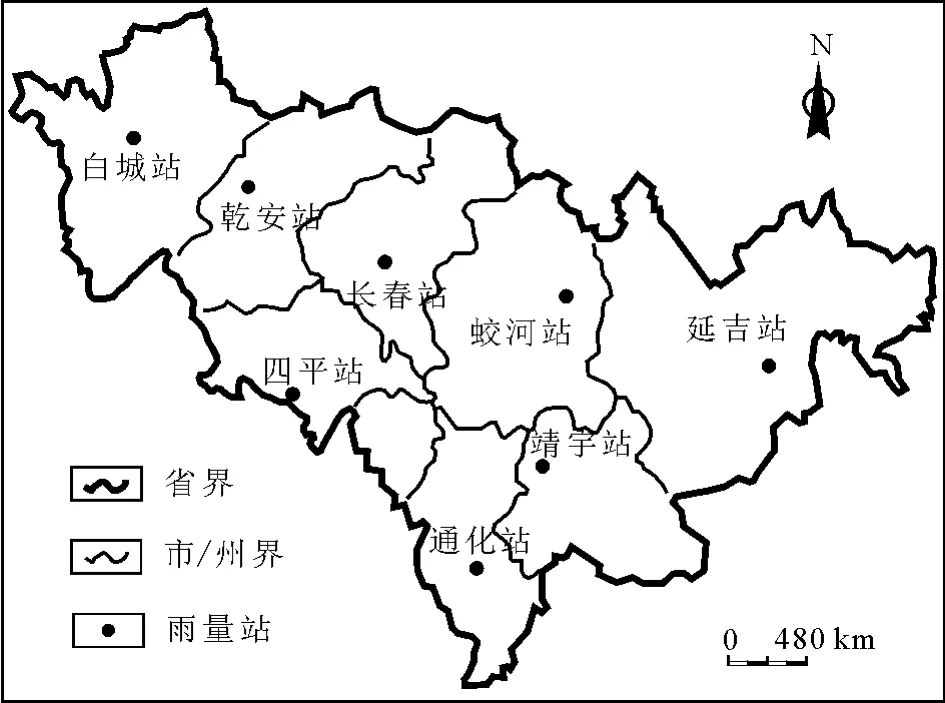
图1 吉林省代表性雨量站分布图Fig.1 Representative precipitation station in Jilin Province

2.2 研究方法

2.2.1 无偏灰色模型

灰色系统是指信息不完全的系统，灰色系统理论以信息不完全系统的行为表现、行为内涵、行为关系、行为环境的层次性、动态性、信息性、量化性为主要目的［7］。灰色理论由邓聚龙教授［8］在1982年首度提出，而后得到了广泛的应用。灰色模型（grey model，GM）使用的是微分方程的动态建模方法，常用的GM是一个一阶单变量的线性微分方程模型，它区别于一般的预测方法，是一种在“贫”信息下针对连续时间序列建模的思路［9］。

对于原始数据序列x（0）＝（x（0）（1），x（0）（2），…，x（0）（n）），利用该数据序列建立无偏 GM（1，1）模型［10－11］，步骤如下：

1）对原始数据进行一阶累加后，形成数列

2）确定数据矩阵B，Yn：

3）最小二乘估计一阶线性微分方程的待估参数α，μ为

4）计算无偏GM（1，1）模型的参数b，A，对呈现指数变化趋势的原始数据序列

作一次累加生成序列

按传统方法建模可得

进而求得以参数α，μ表示的b，A的估计量：

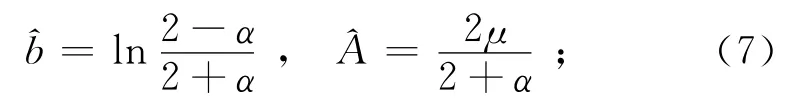
5）建立原始数据序列模型：

其中，当0＜k＜n时其为原始数据序列的拟合值，k≥n时为原始数据序列的预测值。

与传统 GM（1，1）模型相比，无偏 GM（1，1）模型不存在传统GM（1，1）模型所固有的偏差，因而也就消除了传统GM（1，1）模型在原始数据序列增长率较大时的失效现象［12］，其应用范围较传统GM（1，1）模型广泛。此外，无偏GM（1，1）模型无需进行累减还原，简化了建模步骤，提高了模型的计算速度。

2.2.2 灰色马尔可夫链

马尔可夫过程的定义如下：若随机过程X（t）满足

则X（t）被称为马尔可夫过程（马氏过程）。公式（9）右端的条件分布函数

称为马尔可夫过程从时刻tn状态Xn转移到时刻tn＋k状态Xn＋k的概率，简称转移概率。

从定义知，在tn时刻所处状态已知的条件下，马尔可夫过程在时刻tn＋k（k＞0）所处的状态只与其在tn时刻所处状态有关，而与其在tn时刻以前所处的状态无关。这种特性称为马尔可夫过程的无后效性（马氏性）。另外可以证明，马尔可夫过程的统计特性完全由它的初始分布和转移概率确定［13］。

马尔可夫链预测是一种常用的方法，它指对于一系列相依的随机变量，利用马尔可夫链对无偏灰色模型预报值的残差做改进。其基本步骤可概括如下：

1）设原始数据的预报值为，状态⊗i表示原始数据序列相对于预测值的偏离程度，即误差大小，计算误差序列的均值和均方差s，将其划分为m个状态，则任意状态区间的表达式为

式中，⊗i1，⊗i2分别表示误差区间的最小取值与最大取值。

2）根据已建立的分级标准确定各时刻误差序列值所处的状态。

3）计算得到不同步长的马尔可夫状态转移频数矩阵，利用公式求转移概率Pij（m），从而得到转移概率矩阵。式中，fij为第i状态经一步转移 为j状态的频数。

4）利用χ2检验法进行“马氏性”检验。

5）未来状态⊗i和转移概率Pij（m）确定之后，也就确定了预测误差的变动区间［⊗i1，⊗i2］，则预测值可按公式

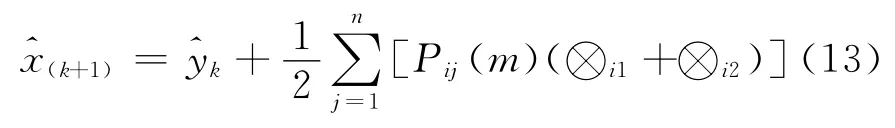
计算。

6）对比预测值与实际观测值，计算相对误差，评价预测效果。

3 结果分析与讨论

3.1 应用无偏灰色模型进行预测

以吉林市（蛟河站）降水量的预测为例介绍无偏灰色马尔可夫链的应用。首先依据灰色原理利用Matlab编程，根据1957 -2000年降水量预报2002-2010年的降水量，计算结果见表1。

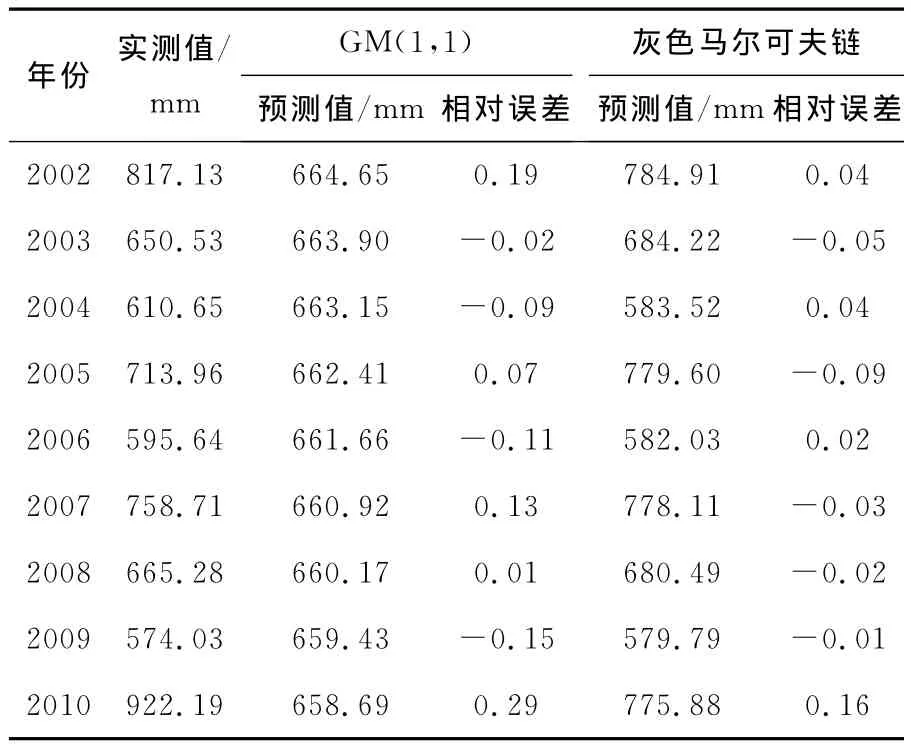
表1 蛟河站降水量预测结果及误差Table 1 Results and error of predication of precipitation in Jiaohe station

由预测结果可知，利用灰色模型（GM（1，1））仅能判断吉林市降水量多年呈递减趋势，预报结果相对误差较大。因此不能直接利用该方法进行预报，考虑用马尔可夫链对误差进行改进。

首先对原始数据进行χ2检验，发现其符合“马氏性”；然后计算预测误差，其均值为19.57，均方差为124.94；再对误差进行状态分级，依据分级标准（表2）确定2001 -2010年预测误差值所处状态，分别为1，4，3，2，3，2，4，3，2，5；一步状态转移矩阵P1的第i行第j列元素表示由状态i经一步转移至状态j的概率，根据公式（12）计算可得。

此时便可根据公式（13），依据2001年的无偏灰色预测值及误差状态预报2002年的降水量；以此类推，可分别计算出2003 -2010年的降水量。计算结果见表1。

表2 误差状态分级标准Table 2 Error status classification standard

通过计算，可得文中所选取的8个代表性雨量站2002 -2010年降水量预测情况，见图2。

3.2 分析与讨论

通过灰色模型预测结果可知：白城、乾安、长春、蛟河、四平、通化6个地区降水量多年呈递减趋势，减幅 分 别 为 0.23%、0.09%、0.24%、1.01%、0.51%、0.54%；延吉、靖宇2个地区降水量多年呈递增趋势，增幅分别为2.60%、0.54%。其主要原因为：延吉与靖宇位于吉林省东南部低山丘陵区，其地势较高，地形起伏较大，水系发育，河流众多；东南部为入海河流的发源地，水量较大，有利于水汽蒸发输送，使气块能够抬升并凝结，在小范围的水气循环中更易于降水的形成。

单纯应用灰色模型预测误差较大，通过马尔可夫链的改进后，误差明显减小，大大提高了预测精度，使预测结果接近实测数值。笔者将预测精度等级分为4类：好、合格、勉强、不合格，其对应的相对误差（绝对值）分别为0.00～0.05，0.05～0.10，0.10～0.20，≥0.20。表3为各测站预测结果的统计情况，计算得知仅17%的预测结果为不合格，因此无偏灰色马尔可夫链适用于吉林省各地降水量的预报。

图2 2002 -2010年降雨量预测情况Fig.2 Predication of precipitation in 2002－2010

将8个测站的均方差与误差（需取绝对值）均值进行归一化处理，见图3，可见二者变化趋势具有很强的一致性；同时利用SPSS统计分析软件做相关性分析，采用Spearman分析方法计算得到相关系数为0.738，显著水平0.037（小于0.050可以接受），说明二者呈正相关，即时间序列的波动性越大预测所产生的误差越大，这就要求预测对象具有过程平稳、等均值的特点［14］。

表3 各测站预测等级年数统计Table 3 Statistical date of predicting level of precipitation station

图3 均方差与误差均值变化趋势图Fig.3 Trend of mean square error and the error of the mean value

4 结论与建议

1）通过灰色模型对降水量变化趋势的预测可知，在2002 -2010年这9年中，吉林省中西部地区降水量呈递减趋势，东部地区呈递增趋势，但变幅不大。

2）在宏观趋势预测方面，无偏灰色模型一定程度上消除了传统模型本身固有的灰色偏差。在微观波动预测方面，无偏灰色马尔可夫模型更具有抗干扰性。经分析，无偏灰色马尔可夫法适用于吉林省降水量的预测，精度较灰色模型法高。

3）当降水量历史数据波动较大时预报精度会降低，因此扩大样本容量或对历史数据进行筛选、处理能一定程度上提高预报效果。

4）对未来降水量进行预报时，可以根据已有历史数据，重新选取样本进行模型构建，重构无偏灰色马尔可夫链转移概率矩阵，达到长期的预测目的，从而为吉林省防洪抗旱工作确定方向。

（References）：

［1］陈社明，卢文喜，罗建男，等.吉林西部气象干旱的多标度分形特征［J］.吉林大学学报：地球科学版，2013，43（1）：245－250.Chen Sheming，Lu Wenxi，Luo Jiannan，et al.Multifractal Characteristic of Meteorological Drought in Western of Jilin Province［J］.Journal of Jilin University：Earth Science Edition，2013，43（1）：245－250.

［2］肖长来，梁秀娟，安刚.模糊均生函数残差模型在地下水数值模拟降水量预报中的应用［J］.吉林大学学报：地球科学版，2004，34（1）：89－92.Xiao Changlai，Liang Xiujuan，An Gang.Application of Residual Error Model of Fuzzy Average－Generated Function in Precipitation Forecasting of Groundwater Numerical Simulation［J］.Journal of Jilin University：Earth Science Edition，2004，34（1）：89－92.

［3］吴春勇，张岩，李泽文.浅谈频谱分析法及其在降水量预报方面的应用［J］.中国环境管理，2007（3）：40－42.Wu Chunyong， Zhang Yan， Li Zewen.Recommendation of Spectrum Analysis and Its Application in Precipitation Forecast［J］.China Environment Management，2007（3）：40－42.

［4］夏乐天，朱元甡，沈永梅.加权马尔可夫链在降水状况预测中的应用［J］.水利水电科技进展，2006（6）：20－23.Xia Letian， Zhu Yuanshen， Shen Yongmei.Application of Weighted Markov Chain to Prediction of Precipitation［J］.Advances in Science and Technology of Water Resources，2006（6）：20－23.

［5］Nourani V，Alami M T，Aminfar M H.A Combined Neural－Wavelet Model for Prediction of Ligvanchai Watershed Precipitation［J］.Engineering Applications of Artificial Intelligence，2009，22（3）：466－472.

［6］李生彪.无偏灰色模糊马尔可夫链预测方法研究及其应用［J］.甘肃联合大学学报：自然科学版，2013，27（1）：19－23.Li Shengbiao.Research of Unbiased Gray Fuzzy Markov Chain Method and Its Application［J］.Journal of Gansu Lianhe University：Natural Science Edition，2013，27（1）：19－23.

［7］邓聚龙.灰色系统理论简介［J］.内蒙古电力技术，1993（3）：51－52.Deng Julong.The Introduction of Grey System Theory［J］.Inner Mongolia Electric Power，1993（3）：51－52.

［8］邓聚龙.灰色控制系统［J］.华中工学院学报，1982，10（3）：9－18.Deng Julong.The Grey Control System［J］.Journal of Huazhong University of Science and Technology，1982，10（3）：9－18.

［9］杨培勇，刘波.灰色拓扑方法在中长期预报中的应用［J］.四川气象，1996，16（1）：31－33.Yang Peiyong， Liu Bo.Application of Gray Topological Methods in Long－Term Forecasting［J］Journal of Sichuan Meteorology，1996，16（1）：31－33.

［10］梅疏影.基于马尔可夫模型的南京市年降水量预测试验［J］.安徽农业科学，2011，39（36）：22415－22419.Mei Shuying.Forecast Experiment of Nanjing Annual Precipitation Based on Markov Model［J］.Journal of Anhui Agricultural Sciences，2011，39（36）：22415－22419.

［11］吉培荣，黄巍松，胡翔勇.无偏灰色预测模型［J］.系统工程与电子技术，2000（6）：6－8.Ji Peirong，Huang Weisong，Hu Xiangyong.An Unbiased Grey Forecasting Model［J］.Systems Engineering and Electronics，2000（6）：6－8.

［12］王铮，和莹.灰色系统建模方法的理论困难及其客服［J］.系统工程理论与实践，1990，10（5）：17－22.Wang Zheng，He Ying.Theory of Gray System Modeling Method and Its Customer Service Problems［J］.Systems Engineering－Theory ＆ Practice，1990，10（5）：17－22.

［13］马占青，徐明仙，俞卫阳，等.年降水量统计马尔可夫预测模型及其应用［J］.自然资源学报，2010，25（6）：1033－1041.Ma Zhanqing，Xu Mingxian，Yu Weiyang，et al.Statistic Markovian Model for Predicting of Annual Precipitation［J］.Journal of Natural Resources，2010，25（6）：1033－1041.

［14］刘宗明，贾志绚，李兴莉.基于灰色马尔科夫链模型的交通量预测［J］.华东交通大学学报，2012，29（1）：30－34.Liu Zongming，Jia Zhixuan，Li Xingli.Traffic Volume Forecast Based on Gray Markov Chain Model［J］.Journal of East China Jiaotong University，2012，29（1）：30－34.