平推式滑坡启动判据的修正

赵权利，尚岳全，支墨墨

1.浙江大学建筑工程学院，杭州 310058

2.长安大学地质工程与测绘学院，西安 710054

0 引言

在近水平砂岩、泥岩互层的岩层，以及松散堆积层覆盖的缓坡区，常常发育滑面倾角一般小于10°的平推式滑坡［1－3］。这类滑坡在我国南方地区，特别是红层发育地区比较常见，其变形破坏的危害性大，对滑坡区居民的经济和生命安全威胁很大［4－6］。平推式滑坡是在坡体后缘静水压力和沿滑移面扬压力的联合作用下，坡体沿层间软弱带被水平推出。滑坡体后缘裂缝中的水头高度决定了坡体后缘所受静水压力及底部扬压力的值，这两部分水的作用力决定了边坡的稳定性［7－8］。当滑坡体处于失稳临界状态时，后缘裂缝的水头高度为临界水头高度。

张倬元等［9］通过研究四川1981年暴雨滑坡群灾害，建立了平推式滑坡启动判据；并通过使用该判据算出的滑坡破坏时后缘裂缝水头高度与实测水头高度的比较来研究该类滑坡的稳定性和破坏机理。范宣梅等［10］通过物理模型试验对平推式滑坡启动判据进行了验证。赵勇等［11］对平推式滑坡滑动时的临界水头进行了统计学分析，通过统计模型的比较，验证了张倬元等提出的基于力学模型的启动判据的合理性。

已有的平推式滑坡启动判据的研究忽略了后缘裂隙水压力在滑面法向上的分力，此忽略项在滑面倾角较大时引起的计算误差较大；同时在公式推导过程中对滑块底部孔隙水压力的分布假设也不准确［12－13］。此两项地下水作用力的简化使得临界水头的计算结果和实际情况有一定的差距。笔者将在前人研究的基础上，对平推式滑坡临界启动判据进行详细推导和修正。建立更合理的启动判据，将有利于平推式滑坡的机理分析，增加此类边坡安全评估的准确度，并提高强降雨期间此类边坡破坏前预警工作的效率。

1 平推式滑坡形成机理

典型的平推式滑坡［7－11，14－17］如图1所示。 此类滑坡一般特点为：坡体透水性差，且底部存在软弱层，软弱层附近存在透水性能较好的层面。一般因坡体蠕变变形，在后缘产生拉裂缝。在强降雨期间，雨水经坡面汇集，由后缘裂缝渗入坡体，后缘水头急剧升高。同时，入渗的地下水沿滑体底部渗透层向坡前渗透。在后缘裂缝处对边坡作用向坡前的静水压力，垂直于裂隙延伸方向；在滑体底部作用滑面法向扬压力。

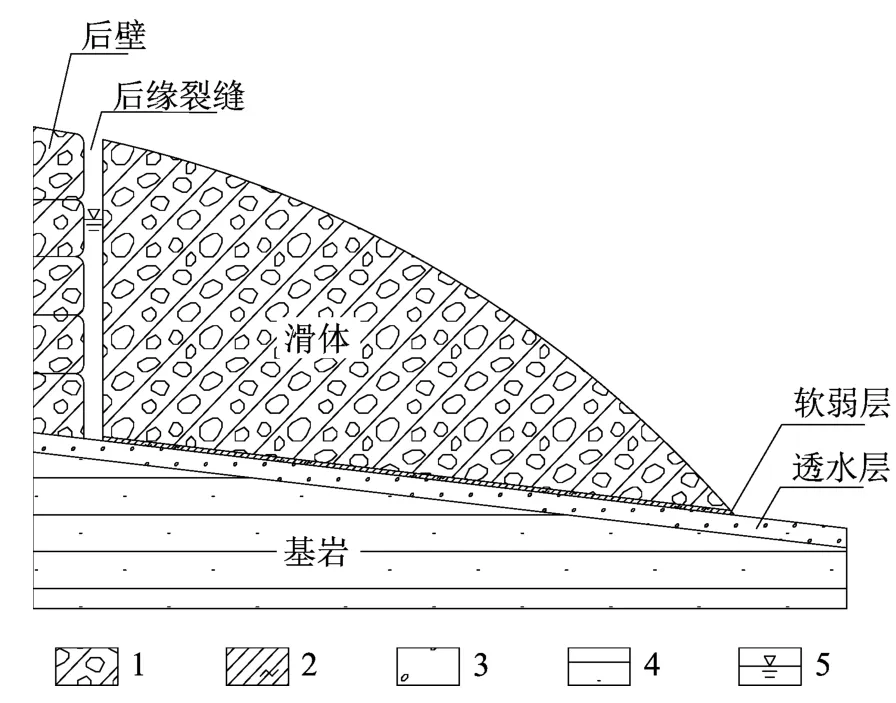
图1 平推式滑坡剖面示意图Fig.1 Schematic profile of translational gliding landslide

随着坡体后缘水位的提高，作用在后缘和底部的地下水作用力迅速增大。因裂缝宽度有限，且降雨期坡面径流能充分补给裂隙水，后缘裂缝中水位上升速度极快。随着后缘水位上升，沿滑面作用在滑面法向上的扬压力增大，使得滑面有效应力减小，滑带土体的抗滑力也迅速减小；同时，后缘裂隙产生水平向推力，增加了坡体的下滑力。坡体后缘静水压力和底部扬压力的作用相耦合，使其整体稳定性急剧降低。

平推式滑坡后缘水头高度决定了滑坡的稳定性。针对特定平推式滑坡案例，在滑面倾角、滑带土强度参数恒定的情况下，当后缘水头超过某一临界高度hcr时，坡体发生滑动。hcr就是平推式滑坡的启动判据指标。对hcr的传统计算方法［9］如下：

式中：α为滑移面顺滑动方向倾角（°）（倾向坡外为正值，反之为负）；L为滑坡底面沿滑动方向长度（m）；φ为滑面摩擦角（°），不考虑黏聚力；W为滑块单宽重力（kN/m）；γw为水的重度（kN/m3）。

2 平推式滑坡启动判据修正

传统计算方法中，简化了滑坡体后缘静水压力沿滑面法向的分力，同时忽略了承压水作用范围的影响，其计算结果有一定的误差。笔者对坡体进行全面受力分析，同时考虑承压水作用范围，从而推导出平推式滑坡修正后的启动判据。

2.1 滑块受力分析

以滑动体为参考系，研究坡体的稳定性。滑块受滑体自重W、坡体后缘裂缝侧向静水压力Pwl、滑体底部扬压力Pwb和滑面摩阻力Sr4个力的作用（图2），当边坡处于失稳临界状态时，有

以滑面为参考系，W、Pwl、Pwb各力都可以分解为沿滑动面法向、切向2个方向的分力，Sr仅沿切向作用。

其中：WN、PwlN、PwbN分别为各作用力在滑面法向上的分力；Wt、Pwlt、Pwbt分别为各作用力在滑面切向上的分力。

传统的计算方法，忽略了PwlN一项，即滑块后缘静水压力沿滑面法向的分力。倾角越大，PwlN越大。如果忽略此项，将导致计算结果准确度降低。

2.2 承压水作用范围的分析

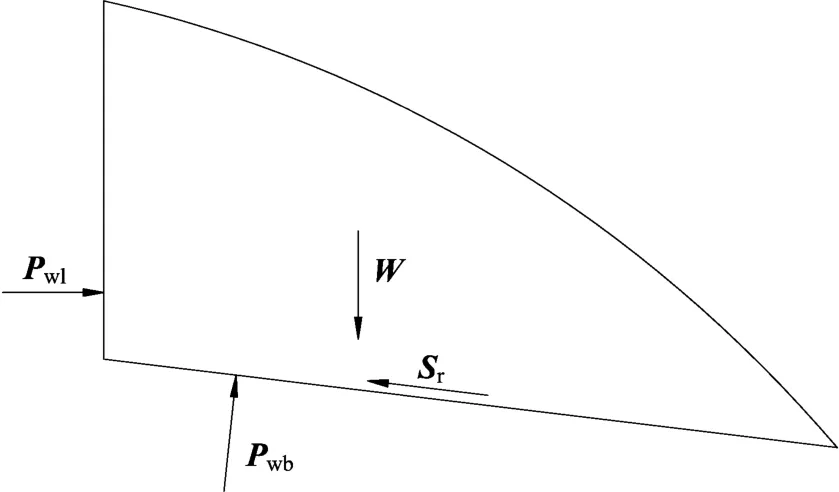
图2 平推式滑坡受力图Fig.2 Force acting on translational gliding landslide

平推式滑坡受水的控制作用比较明显，地下水作用力的大小直接决定了该类边坡的稳定状态。地下水对平推式滑坡的作用主要包括Pwl和Pwb。平推式滑坡中，底部滑面附近的地下水为承压水，Pwb即为滑面附近的承压水孔压。传统方法和笔者所用修正方法对地下水作用的计算方式如图3所示。

图3 地下水作用的不同计算方式Fig.3 Different calculation method for groundwater effect

在丰水期，即连续降雨期或暴雨期，边坡后缘补给流量较大且持续时间较长，此时应采用瞬态分析方法对定流量补给状态进行稳定分析。

由图3可知，地下水的两种计算方式中，Pwl相等，而Pwb的计算方式不同。传统的研究通常假设承压水分布如图3a所示，其中Pwb是一个沿滑面全长的三角形分布力［18］。根据文献［13］的研究，由于平推式滑坡中承压水渗流层存在一定的厚度，所以在不同的渗流情况下，承压水的作用范围一般都小于滑面全长，即Pwb是由底部滑面后侧指向滑面某一点的一个三角形分布力（图3b），该点即地下水状态由承压水转变为潜水的分界点，三角形分布力的作用区间即为平推式滑坡中承压水的作用范围L1。

在平推式滑坡的地下水作用分析中，L1是一个小于L的变量，其计算公式为

式中：L为底部滑面长度；k为渗透系数；q为渗流量；H为滑面附近渗透层厚度。

通过两种计算方式的比较，可以看出在传统计算方式中，直接用L替代L1，往往高估了Pwb的值，使得启动判据计算值偏小，对工程有不利影响。而考虑了L1的计算方法，则是考虑了地下水真实作用的方法，将其用来推导启动判据将更加精确。

实际应用中，应该根据具体边坡的渗流条件，精确考虑各作用力在滑面法向、切向上所有的分量，同时要精确确定承压水作用范围，进而求得更准确的临界水头。

2.3 修正启动判据的推导

实际工程中，平推式滑坡一般的滑面倾角为0°～10°。当倾角越大，PwlN也越大，对hcr的计算结果影响越明显。所以，启动判据中精确考虑PwlN的影响很有必要。

不同的渗透条件下，平推式滑坡对应的L1也不同，受到的地下水作用Pwb也不同，因此其启动判据计算结果也是有差异的。精确分析每一个具体平推式滑坡的L1，可使hcr的求解更加准确。

为了推导平推式滑坡修正启动判据，建立图4所示的分析模型。滑动面倾角α根据实际工程确定，L1如图4所示。图中所示各参数的表达式如式（6）—（10）所示。

其中L1的确定较为关键，见式（6）。

其余各项为

滑块整体下滑力为

图4 平推式滑坡的受力分析Fig.4 Force analysis of translational gliding landslide

滑块整体抗滑力为

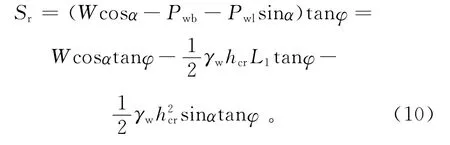
当平推式滑坡启动破坏时，边坡的稳定系数接近临界值，即

因此

将式（9）和式（10）代入式（12）中，整理后可得

解方程可得

将式（6）代入式（14）得

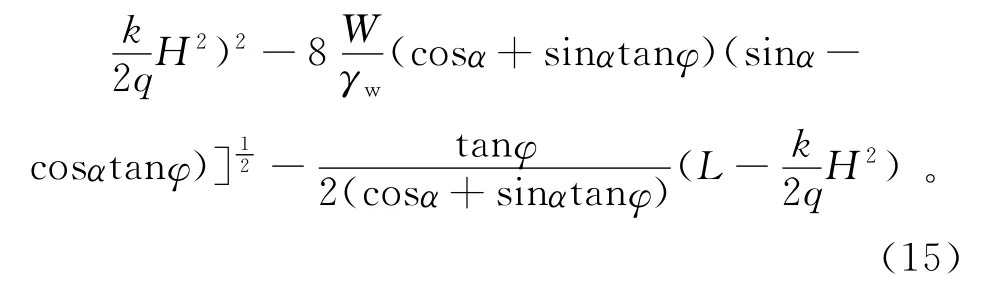
式（15）即是平推式滑坡的修正启动判据，通过α、φ、L、k、q、H、W和γw8个参数可以精确确定平推式滑坡的启动临界水头。笔者所用方法比传统计算方法多考虑了倾角α、承压水作用范围L1。其中，确定L1，比传统方法多考虑3个参数，即k、q和H。

需要指出的是，为了和已有研究进行比较，笔者研究内容是基于传统典型的平推式滑坡模型来进行展开的，即只分析了滑坡后缘拉张裂缝竖直的情况。实际工程中，有部分平推式滑坡的后缘裂缝并不竖直，而是具有一定倾向坡外的倾角，此种类型平推式滑坡影响因素众多，难以用具体的启动判据来表述，故文中暂不予讨论。

3 物理模型试验结果验证

3.1 物理模型试验结果分析

范宣梅等［10］进行了平推式滑坡的物理模型试验，通过在模型槽中设置一个滑动带及其上部三角形滑体来模拟平推式滑坡，后缘水槽来模拟滑坡后缘裂缝，坡体滑动破坏时后缘水槽水头高度作为考察指标，即临界水头高度实测值hcr。

根据文献中已知参数，由式（1）和式（15）分别求得临界水头高度的传统方法计算结果hcrtm和笔者所用修正方法计算结果hcrmm。hcrtm、hcrmm及物理模拟实测结果hcrmv见表1和图5。为了更直观地反映修正方法的合理性，定义相对误差e为

由以上计算结果可知：

1）平推式滑坡启动临界水头的两种计算结果和实测结果的变化趋势基本相同，证明了传统启动判据的基本合理性。两种方法在原理上是相同的，都是基于刚体极限平衡理论，以滑面为参考系，对作用于滑面的4个力进行分析，包括W、Pwl、Pwb和Sr。在分析文中平推式滑坡这种单一滑面的模型时，极限平衡理论具有很高的精度［19］。图5的分析结果也说明了计算结果与实测值基本相符，传统的计算方法是基本合理的。两种计算方法的区别仅在于考虑Pwl和Pwb的大小时有所不同。

表1 试验参数及临界水头高度Table 1 Test parameters and critical hydraulic

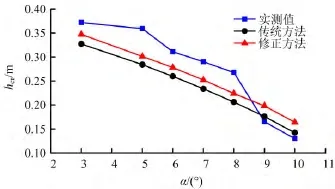
图5 不同方法对应的hcr与α关系曲线Fig.5 Correlation curves between hcrandαcorresponding to different method

2）相对于传统的平推式滑坡启动判据，修正后的启动判据计算结果与实测值更接近、更精确，验证了修正启动判据的必要性和正确性。模型滑面倾角α≤8°时，修正方法计算结果更接近实测值；当α＞8°时，传统方法更接近于实测值，这是因为试验模型调整过程中滑带土受扰动导致实测值相对变小。传统计算方法忽略了Pwl沿滑面法向的分力，同时高估了Pwb的作用范围和大小，因此其计算结果是不准确的，比实测值整体偏小。笔者采用修正计算方法，引入承压水作用范围的概念，充分考虑了地下水作用的实际情况，在平推式滑坡启动判据的推导过程中精确分析每一个力的作用，其结果是平推式滑坡启动判据修正计算结果更接近于试验实测值，这说明修正后的启动判据是更合理准确的。

3.2 修正方法计算值和实测值差异分析

因为实际试验过程中，干扰因素较多，临界水头高度实测值波动较大，其中包含了试验误差。但实测值总体上是符合理论计算结果的。由图5中临界水头修正计算值和实测值曲线可知，实测曲线和修正计算曲线趋势一致，两曲线相交，交点左侧实测值大于计算值，右侧实测值小于计算值。由于试验中滑面倾角α的增加都是整数，为了便于分析，分界点选取为8°，根据滑面倾角可以将试验实测结果分为两段来分析。

1）当α≤8°时，实测值明显大于修正计算结果。其原因有3点：①渗流对边坡作用的时滞性。后缘水头升高，需要经过一段时间才能将地下水的作用完全发挥出来。理论计算公式中，使用的就是某一后缘水头时地下水的最终作用状态。因此，试验中某一水头高度下承压水的作用还未得到全部发挥，实际水头就已经升高了，实测值往往要大于理论值。图6所示为该模型试验的数值模拟结果，当后缘水头从0.15m升高到0.30m时，滑面附近孔压u在滑面长度L上的分布是随时间变化的，进一步验证了承压水作用的时滞性。②模拟试验底部渗透层是由砖块和砂共同铺筑的，其导水性能降低，使得渗透性能减小，地下水作用发挥较慢。进一步增加承压水作用的时滞，使得hcr实测值高于理论值。③渗透层铺筑砖块的部位，几乎不渗透、无水的作用，所以这些部位地下水向上的扬压力作用相对较弱。要达到修正启动判据理论hcr值对应的承压水作用力，则需要更高的后缘水头，故实测值偏高。

图6 后缘水头变化时u和L的关系Fig.6 Relationship between uand Lunder different water level at posterior border of slope

2）当α＞8°时，实测值明显小于修正计算结果。由于地质模型建立，是先按照倾角为0°时填筑，然后底座使滑动面与水平面呈一定的角度。在这个调整的过程中，坡体应力、滑面处应力和强度参数有一个调整过程，使得坡体的稳定性降低了。此时比理论值更小的后缘水头就能使坡体产生滑动。

4 结论

1）考虑承压水作用范围的影响，同时考虑滑坡体后缘静水压力沿滑面法向分力的作用，推导出平推式滑坡修正后的启动判据。2）将修正后的启动判据应用于模型试验分析，结果表明修正方法计算结果比传统方法大6.0%～15.5%，更加接近于试验观测值，修正判据的准确性得到验证。3）对模拟试验结果和修正公式理论进行了比较和分析，指出物理模拟试验结果和理论解存在差距的机理：当边坡模型滑动面倾角小于等于8°时，启动临界水头实测值大于修正计算结果，其原因是渗流的时滞性和渗透层的不均匀性；当倾角大于8°时，启动临界水头实测值小于修正计算结果，其原因是模型稳定性随试验时间增加而逐步降低。

（References）：

［1］殷坤龙，简文星，周春梅，等.万州区近水平地层滑坡和堆积体成因机制与防治工程研究［R］.武汉：中国地质大学，2005.Yin Kunlong，Jian Wenxing，Zhou Chunmei，et al.Study on the Mechanism of the Translational Landslide in Wanzhou District and Prevention Project［R］.Wuhan：China University of Geoscineces，2005.

［2］Jiao J J，Wang X S，Nandy S.Confined Groundwater Zone and Slope Instability in Weathered Igneous Rocks in Hong Kong［J］.Engineering Geology，2005，80（1/2）：71－92.

［3］黄润秋.20世纪以来中国的大型滑坡及其发生机制［J］.岩石力学与工程学报，2007，26（3）：433－454.Huang Runqiu.Large－Scale Landslides and Their Sliding Mechanisms in China Since the 20th Century［J］.Chinese Journal of Rock Mechanics and Engineering，2007，26（3）：433－454.

［4］Jiao J J.A Confined Groundwater Zone in Weathered Igneous Rocks and Its Impact on Slope Stability［C］//Proceedings of the International Symposium on Hydrogeology and the Environment.Beijing：China Enviroment Science Press，2000：602－608.

［5］崔杰，王兰生，徐进，等.金沙江中游滑坡堵江事件及古滑坡体稳定性分析［J］.工程地质学报，2008，16（1）：6－10.Cui Jie，Wang Lansheng，Xu Jin，et al.Stability Analysis of Old Landslide for a Possible Ancient Landslide Event Blocking Middle of Jinsha River［J］.Journal of Engineering Geology，2008，16（1）：6－10.

［6］支墨墨，尚岳全，徐兴华.碎石土滑坡稳定性一元多重属性回归模型分析［J］.吉林大学学报：地球科学版，2013，43（3）：883－890.Zhi Momo，Shang Yuequan，Xu Xinghua.Stability Analysis of Gravelly Soil Landslide Using Multiple Properties Regression Model with One Variable［J］.Journal of Jilin University：Earth Science Edition，2013，43（3）：883－890.

［7］黄润秋，赵松江，宋肖冰，等.四川省宣汉县天台乡滑坡形成过程和机理分析［J］.水文地质工程地质，2005，32（1）：13－15.Huang Runqiu，Zhao Songjiang，Song Xiaobing，et al.The Formation and Mechanism Analysis of Tiantai Landslide，Xuanhan County，Sichuan Province［J］.Hydrogeology and Engineering Geology，2005，32（1）：13－15.

［8］Matjaz M，MatjaˇC，Mitja B.Hydrologic Conditions Responsible for Triggering the Stože Landslide，Slovenia［J］.Engineering Geology，2004，73（3/4）：193－213.

［9］张倬元，王士天，王兰生.工程地质分析原理［M］.北京：地质出版社，2005.Zhang Zhuoyuan，Wang Shitian，Wang Lansheng.The Analytical Principle of Engineering Geology［M］.Beijing：Geological Publishing House，2005.

［10］范宣梅，许强，张倬元，等.平推式滑坡成因机制研究［J］.岩石力学与工程学报，2008，27（增刊2）：3753－3759.Fan Xuanmei，Xu Qiang，Zhang Zhuoyuan，et al.Study of Genetic Mechanism of Translational Landslide［J］.Chinese Journal of Rock Mechanics and Engineering，2008，27（Sup.2）：3753－3759.

［11］赵勇，许模，赵红梅.平推式滑坡后缘启动水头探讨［J］.人民长江，2011，42（17）：32－36.Zhao Yong，Xu Mo，Zhao Hongmei.Discussion on Starting Water Head in Trailing Edge of Translational Landslide［J］.Yangtze River，2011，42（17）：32－36.

［12］吴恒滨，何泽平，曹卫文.基于不同水压分布的平面滑动边坡稳定性研究［J］.岩土力学，2011，32（8）：2493－2499.Wu Hengbin，He Zeping，Cao Weiwen.Stability Study of Slope with Planar Failure Based on Different Water Pressure Distributions［J］.Rock and Soil Mechanics，2011，32（8）：2493－2499.

［13］赵权利，孙红月，王智磊，等.承压水对平推式滑坡的作用分析［J］.岩石力学与工程学报，2012，31（4）：762－769.Zhao Quanli，Sun Hongyue，Wang Zhilei，et al.Influence of Confined Water on Translational Landslide［J］.Chinese Journal of Rock Mechanics and Engineering，2012，31（4）：762－769.

［14］范宣梅.平推式滑坡成因机制与防治对策研究［D］.成都：成都理工大学，2007.Fan Xuanmei.Study of Genetic Mechanism and Control Countermeasures of Translational Gliding Landslide［D］.Chengdu：Chengdu University of Technology，2007.

［15］范宣梅，许强，黄润秋，等.四川宣汉天台特大滑坡的成因机理及排水工程措施研究［J］.成都理工大学学报：自然科学版，2006，33（5）：448－454.Fan Xuanmei，Xu Qiang，Huang Runqiu，et al.The Formation Mechanism of the Tiantai Landslide Induced by Precipitation in Xuanhan，Sichuan and the Design of Drainage［J］.Journal of Chengdu University of Technology：Science ＆ Technology Edition，2006，33（5）：448－454.

［16］刘特洪，林天键.软岩工程设计理论与施工实践［M］.北京：中国建筑工业出版社，2001.Liu Tehong，Lin Tianjian.Design Theory and Construction Practice of Soft Rock Engineering［M］.Beijing：China Architecture ＆ Building Press，2001.

［17］贺可强，阳吉宝，王思敬.堆积层滑坡位移动力学理论及其应用：三峡库区典型堆积层滑坡例析［M］.北京：科学出版社：2007.He Keqiang，Yang Jibao，Wang Sijing.Displacement Dynamics Theory and Application of Accumulational Landslide［M］.Beijing：Science Press，2007.

［18］吕美君，晏鄂川，程江涛.近水平岩层滑坡启动的临界水柱高度分析［J］.岩土力学，2008，29（1）：207－211.LüMeijun，Yan Echuan，Cheng Jiangtao.Study on Critical Depth of Fracture Water for Nearly Horizontal Strata Landslide［J］.Rock and Soil Mechanics，2008，29（1）：207－211.

［19］张鹏.岩土边坡刚体极限平衡法的误差根源与范围研究［D］.西安：西安理工大学，2003.Zhang Peng.Research on the Error－Mechanism and Error－Range of the Rigid Limited Equilibrium Method in the Stability of Rocks ＆ Soil Slope［D］.Xi’an：Xi’an University of Technology，2003.