序列相似性网络聚类与蛋白质家族划分

时逢宽， 李炜疆

（1.江南大学 工业生物技术教育部重点实验室，江苏 无锡 214122；2.江南大学 生物工程学院，江苏 无锡 214122）

随着近年测序技术发展，蛋白质序列数据爆炸式增长。到目前为止，收录信息资源最广的蛋白质数据库 Uniprot（http：//www.uniprot.org）中储存了超过3 600万条蛋白质序列。这些序列已知的蛋白质绝大部分的功能是未经实验鉴定的，必须借助计算方法确定，而聚类方法尤其是近年引起关注的图聚类方法，为从序列解读蛋白质功能提供了一种高效途径。

聚类方法实现蛋白质按功能分类是一个探索蛋白质同源关系的过程，通过序列相似性推断具有共同祖先的蛋白质。实施蛋白质按功能聚类的第一步是获取蛋白质之间功能联系的描述的依据是序列间的相似性关系网络（称为关联图），两两比对相似性分数，这些分数通常可以利用BLAST[1]或FASTA[2]算法高效率地获得。如果待分类蛋白质由集团特征明显的类别组成，亦即同类蛋白质之间的序列相似性显著高于不同类之间的相似性，则传统的聚类法，例如层次聚类，既可方便快捷地实现分类。但是当蛋白质间的序列相似性很低，接近随机涨落区域时，随机成分（噪音）在相似性分数中所占比重越来越大，严重干扰聚类过程，一般的聚类方法就难以奏效，而图聚类（Graph Clustering）则可以更好克服噪音干扰，揭示隐蔽的分类结构。

蛋白质相似性网络通常表示为无向图，图中节点为蛋白质，节点之间的边为序列相似性分数，从而将蛋白质相似性分类问题变换为利用图论的图聚类问题。例如，maximal clique方法通过寻找图中节点之间相互完全连通的子图寻找功能模块[3]，但是蛋白质序列之间无法达到如此高的连接程度，因此只能找到少量的集团；MCL方法通过对相似性矩阵不断交替使用expansion操作和inflation操作，直到矩阵不再变化为止，即为幂等矩阵，对应最后的聚类结果[4]，然而Paccanaro等人研究发现MCL算法很容易产生较很小的集团。作者采用的基于最优模块度的图聚类CD算法[5]，以模块度作为衡量集团结构的强弱的指标，将聚类问题转换为寻找模块度最大的集团，以往的研究表明该算法能用极短时间获得较高质量的聚类结果。本文主要研究：考察当数据关系极其复杂以及数据规模极不均匀时该算法的稳定性；通过不同方法构建邻接矩阵对聚类结果的影响；如何在聚类起始预估最佳阈值范围。

1 数据与方法

1.1 蛋白质序列及家族分类

由于研究内容与蛋白质功能有关，而Pfam蛋白质家族数据库[6]是大量依据功能相关分类的集合。其中的Pfam-A的数据为专家审核维护集合，质量较好可靠性较高；Pfam-B则是利用自动算法划分的未经过人工审核的数据集合。宗族（Clan）[6]是指根据序列相似性，功能相关或隐马尔科夫模型（HMM）收录于Pfam-A中的集合。蛋白质家族是指具有同源性结构域以及序列具有进化相关或者功能相似的蛋白质所形成的集群。家族内在结构上与功能上具有比较强的同源关系，而表现在序列方面则具有显著的序列相似性。集团节点间连接的概率，家族内>家族间>宗族间。同一宗族内部家族成员之间关系与非同宗族相比较而言较为紧密，加大了数据的复杂度以及聚类难度。

蛋白质序列数据来自Pfam数据库26.0版本中人工维护的可信度较高的Pfam-A中获得，选择Multiheme_cytos （CL0317）宗族[7]，包含 9 个家族成员，由于家族间具有一定的进化关系以及家族规模差异较大，该数据能较好的反应实际数据存在形式，本文使用该数据能有效的测试CD算法在家族间联系较为紧密以及家族分歧较大时仍能表现较好的稳定性以及高效性。本宗族中其中一共包含2 210条序列，对于图聚类算法而言，数据结构不均一将影响聚类结果的质量，作者采用的数据集家族内成员在规模上也有较大分歧极度不均一，目的以测试基于模块度最优的CD算法表现。家族内成员的数目分布如表1所示。

表 1 测试数据集（CL0317宗族）中的序列在各家族的分布Table 1 Distribution of sequences in each family in the tested dataset（CL0317）

其总数据、家族内与家族间的相似性分数分布情况如图1所示。

图1为本文采用的数据集的Score分布情况。由于采用BLAST计算相似性分数时，只报告相似性显著的序列对（E＜10）。从数据分布情况可知家族内序列对相似性显著比例较高序列之间连接紧密，相反家族间的结连接为稀疏，使得采用模块度的图聚类进行蛋白质分类成为可能。家族内相似性不显著的序列对约占家族内总数据的30%，家族内的序列相似性分数分布的峰值处于30附近；不仅如此，来自不同家族间的序列相似性显著的序列对约占19%，其Scores峰值也在30附近。这些不正确的序列关联严重干扰聚类过程中序列的正确分类，例如简单依据相似性距离的层次聚类。

图1 家族内与家族间的相似性分数分布情况Fig.1 Distributions of sequence score between pairs of sequences.Note that the main parts of the distributions are in the fluctuation region with very low sequence score

图2中的“点”为两条序列节点之间有BLAST报告的，即序列之间相似性显著。由于家族内成员之间相似性显著所占比例大于家族间，从而形成图中所示的块状结构，而由图1中的家族间相似性显著序列也占有一部分，从而导致图2中家族之间的界限比较模糊，家族间相互联系互相干扰使得聚类难度增大。

图2 所有BLAST报告中序列之间相似性E-value＜10的稀疏结构图Fig.2 Spy plot of the similarity between all sequence pairs reported by BLAST all-against-all search with E-value＜10.Each dot represents a significant match between the corresponding pair of sequences

1.2 算法简介

图聚类在最近几年广泛的应用于各个领域学科例如生物信息学、模式识别、社会社交等[8-17]，特别是采用网络模块度的图聚类方法得到了更高的关注。模块度是由Newman和Girvan[8-20]提出的用于衡量聚类结果中网络集团结构特征强弱的指标，通过搜索使模块度最大化的集团划分，即可实现网络节点的聚类，例如将蛋白质划分为不同家族。模块度最大化是NP困难问题，没有快速精确求解方法，只能用近似方法寻求次优解。CD算法[5，20]是一种高效的模块度最大化算法，在众多实际应用问题中表现出良好性能，因而选作本文的图聚类算法。

1.3 邻接矩阵构造方法

蛋白质相似性网络是基于序列之间相似性定义的，表示蛋白质之间的相似程度，通常是赋权图，其中节点为蛋白质，边的权重为利用BLAST获得的序列两两比较的E-value（E值）或Score（S值）。当两个序列的相似性临近随机涨落区域时，其BLAST报告的E或S分值就由随机因素主导，从而逐渐失去了精确量化相似程度的意义，将这些分数直接输入聚类算法就可能干扰聚类结果。因此在本文中，采用非赋权图表示蛋白质相似性网络，其中的边仅表示存在相似关系而不包含程度信息，相应的邻接矩阵由0和1构成。采用非赋权图还可以显著降低图聚类的算法复杂度。

本文BLAST报告的E值和S值为基础，采用阈值过滤方式构建邻接矩阵，考察不同的阈值对聚类结果的影响，寻找最佳阈值。基于S值构建邻接矩阵可以表示为

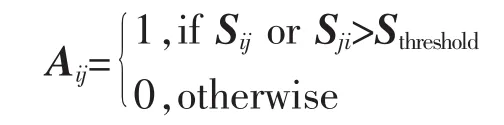
其中 i，j表示蛋白质；Aij为邻接矩阵的 （i，j）元素，表示蛋白质i与j之间是否存在相似关系；Sij为蛋白质i与j之间的BLAST相似性分数；Sthreshold为给定的阈值。 由BLAST计算得到的相似性分数矩阵不是严格对称的，亦即Sij与Sji有差异，对此我们采用取最大分数使其对称化。

当以E值为基础构建邻接矩阵时，采用如下过滤方式

1.4 聚类结果与已知分类一致性的评估方法

聚类结果所对应的Q值反应了在给定聚类模型下，算法寻找最优解的能力。为了评价聚类结果与蛋白质家族分类的一致性，我们采用归一化互信息 NMI（Normalized Mutual Information）描述聚类结果与目标分类的吻合程度，其定义为[23-24]

其中A表示蛋白质家族分类；B表示聚类结果；cA表示家族数；cB表示聚类结果的集团数；Nab表示家族a的成员中在聚类结果中划分至集团b的数目；由Nab构成的矩阵称为混淆矩阵（confusion matrix），刻画了不同分类之间的相互关系。为家族a中蛋白质总数，为聚类结果中属于集团b的蛋白质数目。

NMI的数值是介于0与1之间，越接近1则聚类结果与目标分类的一致性就越好，当NMI等于1时，实际分类与目标分类是完全等价的。

2 结果和讨论

采用的图聚类算法CD是随机算法，每次运行得到的结果都略有差异，多次重复运算可以获得更好的结果。为了获得尽可能稳定的分类结果，在一次聚类计算中重复运行CD程序，一般说来，运算次数越多，以模块度衡量的计算结果越好，当然需要的计算量也越大。在一定阈值下构建邻接矩阵，测试了选取不同运算次数时算法稳定性的表现，结果见图3。

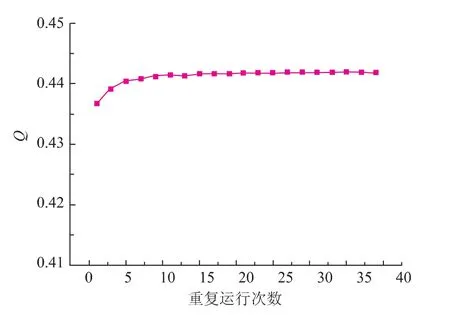
图3 不同的重复运行次数与最优模块度QFig.3 Best modularity （Q）values obtained in multiple runs of the CD algorithm with different replication numbers.The mean values and standard errors were calculated on 100 outputs of multiple runs

随着运算次数的增加计算的次数大幅增加，Q值平均值增加，但是波动逐步减小，随着运算次数的增加稳定性逐步增强，因此在合适的配置数下能减小算法随机波动所导致的误差，综合考虑选择相同情况下运算程序10次，然后取Q值最大时为最优解。

作者使用的CD算法通常不需要调整参数，只需将初始最大集团数目（nslots）设置为大于可能的最终分类数即可，CD算法在优化搜索过程中能够自动缩减分类数至合适的数值。测试结果也表明当nslots足够大时，聚类结果不依赖于nslots的具体取值，故固定选取nslots=100。

选取不同的阈值得到的邻接矩阵也不同，进而影响最终聚类结果。对于数据集CL0317，采取多个阈值构建邻接矩阵然后计算CD聚类，结果见图4。图中每个阈值对应的CD聚类均重复100次，考察算法的平均性能和稳定性。

图4 使用NMI衡量邻接矩阵对聚类结果的影响Fig.4 Influence of the adjacency matrix on the clustering performance measured by normalized mutual information. The adjacency matrices are constructed by filtering A）similarity scores and B）E-values with varied thresholds.

由图4可见，基于E值与基于S值得到的聚类性能没有明显差异。以S值构建邻接矩阵时，最佳聚类结果在Sthreshold=29附近获得，但是在Sthreshold=25～33这样一个很宽的范围内，平均NMI值起伏很小，表明聚类方法对于邻接矩阵的适度宽容性。

当采用非常严格的相似性标准，即Sthreshold远大于最佳阈值时，相似性图中因随机效应导致的错误连接大量减少，同时真实反映序列关联的正确数据也被过滤掉，使得聚类依据不足从而性能明显下降。相反，过于宽松的阈值（即Sthreshold很小）使得相似性图中随机连接大量增加进而降低聚类准确性。

当以E值为基础构建邻接矩阵时，结果是类似的，最佳聚类性能在lgEthreshold=-2～0较宽的范围内达到。我们注意到，这样的相似性标准比通常采用的BLAST 标准（E～10-5—10-2）宽松，说明此时的相似性图中含有较多的随机误差数据，采用的聚类方法能够满意地从噪音数据中提取正确的分类信息。

采用Pfam数据库中人工维护审核的Pfam-A数据库中的一个宗族，由于宗族内的家族成员之间有着一定关系，与非宗族内的蛋白质数据相比聚类难度大。图聚类中家族大小规模不均匀分或分歧度较高是聚类分析中比较难以聚类的情况，作者挑选这一宗族Paired_CXXCH_1家族有479条序列，小的GSu_C4xC__C2xCH家族只有15条序列，两者相差数十倍，详见表1，这样的数据集是典型蛋白质家族关系，从而本实验的结果更能说明利用序列相似性网络基于模块度的CD聚类算法的优良性能和通用性。

综合结果可以发现，邻接矩阵的构建方法对聚类结果有着较为密切联系，并且使用基于模块度的CD算法能够有效的挖掘网络内在的集团结构，并将有效信息从包含大量噪音的数据中提取出来。由于随着构建邻接矩阵采用的阈值限定的增强 （减弱）节点之间的联系减少（增多），噪声减少（增强），节点之间连接正确率增高（降低），导致图聚类算法的可用信息逐步减少（增多）。阈值限定的增强导致节点之间的连接减少，形成大量的孤立点，从而算法无法判断其所属导致聚类结果下降；阈值限定的减弱导致节点之间的连接增多，有用信息量增加的同时引入大量的错误信息，正确数据淹没在大量的噪声中使得算法无法正确判断分类信息。研究表明：尽管采用不同类型的相似性分数作为构建邻接矩阵的阈值，CD算法仍能在较为宽松的阈值范围内从包含大量噪声的数据中识别出具有功能的集团结构，即只要输入CD算法的邻接矩阵包含有足够多分类信息，该算法就可以获得与实际结果一致性较高的聚类结果。而对于采用single-linkage层次聚类的聚类结果分析得到NMI数值为0.028，形成了巨大的一个集团与一些零散的小集团，相比采用CD算法的NMI值为0.778，结果明显更加合理。通过分析表明CD图聚类算法聚类结果最优阈值与图1中总数据、家族内和家族间数据分布峰值是一致的，通过本文的研究使得聚类前对数据分布分析可以估计最佳阈值范围。

由于家族内外的序列相似程度的高低差异，由图1的相似性分布可知白质序列家族划分不能简单依据相似性进行蛋白质家族划分。Pfam-A中的蛋白质家族为检验本实验结果的准确性提供了数据支持，蛋白质之间的相似性分数可以通过BLAST进行一一比对获得，采用不同的相似性数值构建相似性矩阵，矩阵节点之间的权重采用不同的相似分数，依据构建的相似性矩阵采用不同的阈值构建邻接矩阵，本实验重点研究不同的相似分数以及不同阈值构建邻接矩阵对CD算法的结果的影响，并得出阈值只要在较宽松范围内聚类结果都比较理想，并且该区间与数据集自己身分布有关，最佳阈值在数据分布峰值附近。当选取的阈值大于峰值时，由于较多的有用信息被去除，从而导致许多孤立节点，使得聚类算法无法判断其分类信息，使得聚类结果质量下降；当选取阈值过小于峰值时，有用信息增多的同时噪声大量增加，也使得无法正确划分其分类信息；因此采用合适的阈值能去除一部分噪声的干扰有助于聚类算法识别有用信息。利用序列相似网络的CD图聚类法对蛋白质家族划分，从本实验结果与实际的平均吻合程度上分析该方法对蛋白质序列家族划分有较高的准确率。所以综合考虑利用CD算法用于序列相似网络聚类分析在蛋白质家族划分方面是一种高质量的聚类方法。

[1]Altschul S F，Gish W，Miller W，et al.Basic local alignment search tool[J].J Mol Biol，1990，215（3）：403-410.

[2]Pearson W R.Effective protein sequence comparison[J].Meth Enzymol，1996，266：227-258.

[3]Spirin V，Mirny L A.Protein complexes and functional modules in molecular networks[J].PNAS，2003，100（21）：12123-12128.

[4]Enright A J，Van Dongen S，Ouzounis C A.An efficient algorithm for large-scale detection of protein families[J].Nucleic Acids Research，2002，30（7）：1575-1584.

[5]Mei J，He S，Shi G，et al.Revealing network communities through modularity maximization by a contraction-dilation method[J].New Journal of Physics，2009，11（4）.

[6]Punta M，Coggill P C，Eberhardt R Y，et al.The pfam protein families database[J].Nucleic Acids Research，2011，40（D1）：D290-D301.

[7]Mowat C G，Chapman S K.Multi-heme cytochromes—new structures，new chemistry[J].Dalton Transactions，2005（21）：3381-3389.

[8]Foggia P，Percannella G，Sansone C，et al.A graph-based clustering method and its applications[Springer Berlin/Heidelberg.2007：277-287.

[9]Bello-Orgaz G，Menéndez H D，Camacho D.Adaptive k-means algorithm for overlapped graph clustering[J].Int J Neural Syst，2012，22（5）.

[10]Santini G，Soldano H，Pothier J.Automatic classification of protein structures relying on similarities between alignments[J].BMC Bioinformatics，2012，13（1）.

[11]He J，L C，Y B，et al.Efficient and accurate greedy search methods for mining functional modules in protein interaction networks[J].BMC Bioinformatics，2012，13.

[12]Seah B S，Bhowmick S S，Forbes Dewey C，Jr.Facets：Multi-faceted functional decomposition of protein interaction networks[J].Bioinformatics，2012，28（20）：2624-2631.

[13]Solava R W，Michaels R P，Milenkovic T.Graphlet-based edge clustering reveals pathogen-interacting proteins[J].Bioinformatics，2012，28（18）：i480-i486.

[14]Healey C G，Dennis B M.Interest driven navigation in visualization[J].IEEE Trans Vis Comput Graph，2012，18（10）：1744-1756.

[15]Becker E，Robisson B，Chapple C E，et al.Multifunctional proteins revealed by overlapping clustering in protein interaction network[J].Bioinformatics，2012，28（1）：84-90.

[16]González A J，L L，W C H.Predicting ligand binding residues and functional sites using multipositional correlations with graph theoretic clustering and kernel cca[J].IEEE/ACM Trans Comput Biol Bioinform，2012，9（4）：992-1001.

[17]Qian P，Chung F L，Wang S，et al.Fast graph-based relaxed clustering for large data sets using minimal enclosing ball[J].IEEE transactions on systems，man，and cybernetics.Part B，Cybernetics ：a publication of the IEEE Systems，Man，and Cybernetics Society，2012，42：672-687.

[18]Newman M E J，Girvan M.Finding and evaluating community structure in networks[J].Phys Rev E Stat Nonlin Soft Matter Phys，2004，69（2 Pt 2）.

[19]Girvan M，Newman M E J.Community structure in social and biological networks[J].PNAS，2002，99（12）：7821-7826.

[20]M J，Y X，Z W.Revealing remote protein homology with sequence similarity and a modularity-based approach[J].Theor Biol Forum，2011，104（1）：57-68.