贝叶斯认证理论与证据支持关系探析
黎红勤
(中山大学哲学系,广州 510275)
一、引言
科学认证理论主要是关于科学推理以及科学假说的接受与评价问题,试图回答证据如何支持假说,实验结果对假说产生何种程度的支持。贝叶斯认证理论作为一种定量的认证方法,引入了测度相关性(relevance measure)函数Cpr,通常贝叶斯认证是关于证据、假说、背景知识的三元关系,因此有:当 Cpr(h,e,K)>0时,即 P(h|e,K)>P(h|K),e认证 h;当 Cpr(h,e,K)=0时,即 P(h|e,K)=P(h|K),e无关于 h;当 Cpr(h,e,K)<0时,即 P(h|e,K)<P(h|K),e否证h。我们知道贝叶斯认证理论的理论基础是概率的主观主义解释,即将概率解释为主观置信度。因此,在上面的式子中,P(h|K)是验前概率,即没有获得证据e时认知主体对假说h的置信度,P(h|e,K)是验后概率,即认知主体得知证据e后的概率,验前概率和验后概率只是针对e而言的。正相关认证函数是一种比较常用的测度相关性函数,在贝叶斯认证理论中得到比较普遍的应用,即d(h,e)=P(h|e,K)-P(h|K)。①测度相关性函数有很多种表达方式,除了正相关测度函数之外还有对数比例测度r(h/e)=log[P(h/e)/P(h)]以及似然比对数测度l(h,e)=log[P(e/h)/P(e/~h)]。不过在使用哪个测度相关性函数的问题上,贝叶斯阵营内是有分歧的。不仅如此,测度函数的多样性产生了贝叶斯的“测度敏感性”问题,即不同的测度函数测出证据对假说的认证度是不一样的,这也是贝叶斯认证理论面临的一个重大挑战之一。
贝叶斯认证理论简单却有力,由于它能通过测度相关性函数测度认证的程度,因此比常规的定性的认证理论要优越。它的颇富解释力的描述分析和相应的规范功能成为当代科学推理和科学假说检验与评估的主流方法论,但是它也面临着一些挑战,比如胡贝尔问题与旧证据问题。
胡贝尔(F.Huber)认为根据贝叶斯定理可推出证据的可靠性与认证度的反比关系,他进一步认为这种有违直觉的关系构成了对贝叶斯认证理论的主要责难,而格利莫(C.Glymour)提出的旧证据问题则是这种不统一的反比关系更深刻的描述。笔者将表明证据的可靠性与认证度的反比关系并不是贝叶斯认证理论和科学家实践的分歧,恰恰相反,贝叶斯认证理论如实地反映了科学家的实际行为。
要正确认识证据对假说的认证效力,我们就需要重新审视证据对假说的支持关系。常规的认证理论将证据对假说的支持关系看作是一种单一的静态关系,然而通过贝叶斯认证理论对证据支持关系的分析,我们不难看出假说与和证据之间的支持或认证关系是复合多元的,并且呈现出一种动态发展关系。所以有时就会呈现出如胡贝尔所说的证据的可靠性与认证度之间的反比关系。我们先来看看胡贝尔的证据可靠性与认证度之间的反比关系问题如何对贝叶斯认证理论造成了“冲击”。
二、证据的可靠性与认证度的反比关系
根据胡贝尔的论述,假设在时间t1背景知识为K1,而在时间t2背景知识为K2,认知主体知道K和h可逻辑推出e。随着时间不同证据对假说的认证度会发生变化,根据正相关认证测度函数有:
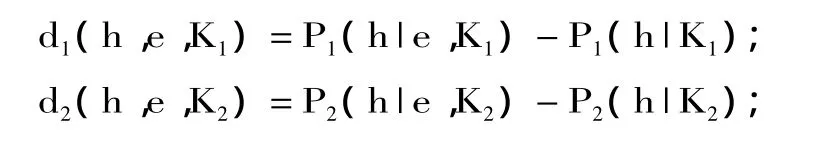
根据贝叶斯定理分别得到:
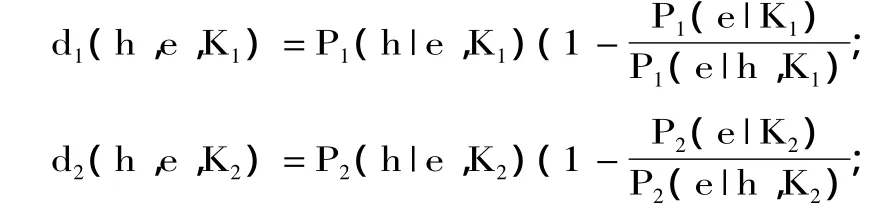
假定从t1到t2背景知识并未变化,则有K1=K2,根据杰弗里条件化规则,有 P1(h|e,K1)=P2(h|e,K1)=P2(h|e,K2)。e是 h与 K 的逻辑后承,故有 P1(e|h,K1)=P2(e|h,K2)=1,综上有:
(1)d1(h,e,K1)> d2(h,e,K2),当且仅当P2(e|K2)> P1(e|K1)[1]。
上式表明,如果P2(e|K2)>P1(e|K1),即:比起t1时刻,在t2时刻证据e的可靠程度更高,但是我们却得到 d1(h,e,K1)> d2(h,e,K2),即在 t2时刻证据e对假说h的认证度比起t1却更小。更一般地,如果e的概率很小,即极不可能的事情竟然发生了,它对假说h的认证度反而会很大,而如果e极其可信,那么它对假说的认证度反而会很小。似乎贝叶斯认证理论得出的结论和我们的直觉不符,即证据e越可靠,那么对假说的认证程度就会越高。
笔者认为并不像胡贝尔所说的,式(1)构成了对贝叶斯认证理论的责难,笔者将要表明式(1)并没有造成贝叶斯认证和科学家实践的分歧,恰恰相反,贝叶斯认证理论如实地反映了科学家的实际行为,我们的直觉只是出于对科学行为的误解。
科学家在检验一个假说时一般的操作是,先构建一个理论模型,然后在这个模型基础上做出预测,随后设计实验并获得数据或结论,接下来比对实验结论与预测之间是否一致。一个检验通常包括一些实验设置及其实验初始条件,当然实验的设计并不能完全达到理想的环境,因此就需要一些辅助性的条件,这些辅助性条件控制的好坏会影响实验获得的证据的可靠性。
我们以贝尔不等式的判决性实验来说明。1965年贝尔(John Stewart Bell)在《论EPR佯谬》一文中根据“可分离原则”导出了一个双粒子自旋系统的不等式,叫“贝尔不等式”。这一不等式显示了相对论所要求的“定域性”与量子力学之间的深刻矛盾,并提供了利用实验来进行判决的可能性。如果“贝尔不等式不成立”则爱因斯坦的“可分离性原则”就成立,否则玻尔的“不可分离性原则”就成立。
在1972年后的30年里,伯克利、哈佛和得克萨斯等地陆续公布了不少验证贝尔不等式的典型实验,其中大多数是用原子的级联放射产生的关联光子对做的,并且大多数的实验结果都同量子力学的预期一致,但由于实验设计方案离理想实验较远,因而有的实验结果可靠性不高。1982年阿莱恩·阿斯派克特、达利巴德与罗哲等人对EPR作出检验,他们用非线性激光激励原子级联放射产生孪生光子对来做实验,该实验采用了双波导的起偏器,实验方案也如同EPR理想实验一样,实验结果和量子论的预言完全符合。而后许多物理学家都重复阿斯派克特的实验,并且运用更新的手段,使实验模型越来越靠近爱因斯坦当年那个最原始的EPR设想。马里兰(Maryland)和罗切斯特(Rochester)则采取非线性地分出紫外光子的办法来产生EPR关联光子对,使验证实验更为精确和客观。1998年,奥地利因斯布鲁克大学(Innsbruck)的实验团队的实验表明了孪生量子实体的不可分离性即非定域性,他们最后作出的结论是:实验结果极为优势地同量子力学的预期一致,无可置疑地违反了贝尔不等式。2003年,皮特曼(Pittman)和法兰森(Franson)则报道了产生于两个独立源的光子对于贝尔不等式的违反[2]。
我们看到关于“贝尔不等式”的整个动态的检验过程,正是显示了前文所阐述的思想,即证据的可靠性与认证力度是呈反比关系的。由于贝尔不等式验证条件要求颇高不易实现,因此1982年阿莱恩·阿斯派克特的实验虽然比起之前的实验精确度是一个很大的提升,但在很多科学家看来实验的可靠性并不是很高,然而毫无疑问它对量子力学却是极大的认证,整个学界会为它的检验结果而热血沸腾。后续的实验提高了证据的可靠性,而其认证度远无法和阿斯派克特的实验相比,也就是说随着证据的可靠性提高其支持力度却逐渐削弱。而此时要想获得更高的认证就必须采用新的实验方法或者改变实验设置,比如马里兰(Maryland)和罗切斯特(Rochester)采取非线性地分出紫外光子的办法,而皮特曼(Pittman)和弗兰森(Franson)则诉诸于两个独立源的光子对。
因此,重复实验的目的就是为了消除证据的不确定性,而一旦科学家认为产生证据的实验控制足够精确即证据足够可靠,科学家就认为没有什么可质疑的,这时科学家赋予该证据为1的概率,即将它归入背景知识。马斯格雷夫(A.Musgrave)提到,经过多次重复实验后,科学家会发现同样的实验设置只会得出类似的结果。他提议将这些普遍规律加入背景知识,并且基于这些背景知识我们可以预测下一次的实验会得出类似的结果。因此他认为,可以用P(e|h&K)-P(e|K)来测度e是否可以认证h。显而易见,如果e被归入背景知识,则有 P(h|e &K)=P(h|K)[3]。这个时候证据e对被检验的假说的认证度就为0,因此很多科学家也就不再展开类似的实验来提高对假说的认证,因为证据不能无限度地认证假说,也就是证据对假说存在有限认证,科学家的直觉和贝叶斯方法的结论并无不同。通常在这之后科学家有两种做法:第一种就是充分肯定假说的可靠性,并将其视为成功的理论体系;第二种就是寻求其他不同的证据的认证,即寻求多样化的证据来实现对假说的进一步认证。
假设e是已发现过的证据也就是旧证据,则有P(e)=1,假说 h能够推出e,则P(e|h)=1,根据贝叶斯定理得到P(h|e)=P(e|h)P(h)/P(e)=P(h),因此e不能认证假说。这就是通常意义上的旧证据问题。反贝叶斯主义普遍认为,旧证据问题造成了对贝叶斯方法的主要责难。这里的旧证据存在概念的混淆,笔者在另一文中尝试对旧证据问题进行了澄清[4]。不过值得补充的是,陈晓平提出了一个消解旧证据问题的方案,可以说为贝叶斯的发展扫清了障碍[5]。
而要进一步阐明贝叶斯认证理论,我们有必要重新审视假说与证据支持之间的关系。常规的认证理论将证据对假说的支持关系看作是一种单一的静态关系,甚至在逻辑实证主义那里,认证完全是一种纯粹的逻辑关系,这恰恰是库恩的理论要致力批判的。从下文贝叶斯认证理论对证据支持关系的分析中,不难看出证据和认证度之间的关系是复合多元的,并且呈现出一种动态发展关系。根据贝叶斯定理,即P(h|e)=P(h)P(e|h)/P(e),我们得到e对h的认证度决定于证据e的概率以及证据e对假说的似然性(有时也称为预测度)。也就是说证据对假说的支持度和证据的概率,以及证据的似然性息息相关,而证据的数量,证据的精确性、多样性、新颖性和证据增加的速度等等都会影响认证度。不仅如此,假说对证据的解释能力、证据对假说的预测程度也影响了证据对假说的支持度。下面我们将从证据的意外程度、证据的有限认证两方面展开。
三、假说与证据支持
常规认证理论认为在缺乏不利证据的情况下,一个假说的认证通常是随着有利检验结果的增多而增加的。我们知道假说的某个逻辑后承e可以认证假说。豪森深入探讨了这种认证关系[6]120。对于假说 h,e1、e2、…、en是他的一系列逻辑后承,并且对于所有i有P(ei|h)=1;令en=e1&e2&…&en,对于所有 n 有 P(en|h)=1,结果有P(h|en)=P(h)/P(en),由此得到:
P(h|en)=P(h)/P(e1)P(e2|e1)P(e3|e1&e2)…P(en|en-1);
上式表明,由于ei是h的逻辑后承,此时h的验后概率决定于验前概率与全证据的概率。如果P(h)>0,随着 n趋近于无穷,P(en|en-1)必定会趋近于1,即此时 P(h|en)趋近于 P(h|en-1),即en-1和en对h的认证并无实质上的区别。这个论证来自杰弗里斯,我们简要地阐述一下:
在具体的科学事件中,针对假说h,我们做出不同预测,比如基于牛顿经典物理体系下,我们可以有很多不同的模型,包括自由落体,抛物线运动,单摆的摆动等等。这些模型都是牛顿万有引力模型的逻辑后承,我们将牛顿引力模型记为h,而自由落体为hr,hr为h的逻辑后承。hr有一系列的逻辑后承即e1、e2…en,由于hr是h的逻辑后承,e1、e2…en也者是h的逻辑后承。根据贝叶斯定理:
P(h|en)=P(h)/(P(e1)P(e2|e1)…P(en|en-1));
且有P(hr|en)=P(hr)/P(e1)P(e2|e1)…P(en|en-1))。
将上面的两个公式合在一起,消去P(e1)P(e2|e1)… P(en|en-1)就得到:
P(h|en)/P(hr|en)=(P(h)/P(hr));
等式两侧分别乘以P(hr|en)得到:
P(h|en)=(P(h)/P(hr))P(hr|en)。
由于P(hr|en)必定小于或等于1,于是我们从上式得到:
P(h|en)≤P(h)/P(hr)[6]120-122;
这意味着,同一种类型的证据即hr的逻辑后承e1、e2…en对假说h的验后概率有一个上限,即:P(h)/P(hr),进而使这些证据对h认证度也有一个上限。正因为此,科学家们设计了某项实验并通过认证以后,一般会停止此类实验,转向其他模型其他的实验来认证假说。比如,对于牛顿体系,科学们不会一直重复地进行和审查有关自由落体运动的证据,而是转向研究单摆运动、双星缠绕定律、月球引力引起的潮汐现象,或者是哈雷彗星的周期,进而对理论展开新的检验,并从中取得不同类型的证据。这就是说,证据的多样性对于提高假说的认证度是必不可少的。亨普尔曾仔细分析斯奈尔定律检验并考察了多姆山实验,阐明了多样性的证据的重要意义[8]。
让我们继续探讨证据支持这种关系。举个例子,爱因斯坦的“不可能环”的发现对广义相对论是个极大的认证。根据爱因斯坦广义相对论,来自遥远星球或类星体的光线或放射波绕过巨大的前景物体到达地球的路程中会发生引力收缩,物体的引力将使射线发生弯曲,因此将产生一个或多个变形的光源成像。根据爱因斯坦理论预测的这种不同寻常的天文现象“不可能环”竟然实现了,天文学家用射电望远镜矩阵,意外地发现在狮子星座中的物体由于重力透视效应的影响已经呈现出了一个完整的环状。
证据越是意外则认证度越高,这是贝叶斯理论的自然效应。因为贝叶斯定理P(h|e)=P(h)P(e|h)/P(e)右边的分母P(e)表示预测证据的置信度,其值越低越不可信,因而越令人感到意外。在上例中,爱因斯坦指出,只有当光源和收缩物体与地球精确地处于同一直线时,成像才有可能形成一个完整的光环——这似乎是不太可能的事情,对于我们而言,由于这种及其苛刻的条件意味着证据的概率即P(e)几乎趋近于零,证据e即发现“不可能环”意外程度很高。在这种情况下根本不可能发生的意外事情e竟然发生了,导致P(h|e)>>P(h)。这表明,贝叶斯理论很好地刻画了证据的意外度与它对假说的认证度之间的正相关性。
豪森举了一个生活的例子[6]123,假如一个所谓的通灵师预测你晚上会遇到一个陌生黑人,你可能会不屑一顾,即便是真正发生了,你只会认为他只是碰巧猜对了。但如果通灵师不单预测到了这个陌生人还预测到这个人头上有多少头发,那么当这个预测成真时,你之前的疑虑大概就会消失,进而很大程度上确信他可能真的掌握通灵术。否则,他怎么会预测的那么准确呢?对此,我们还可根据贝叶斯理论作如下说明:
根据贝叶斯定理有:
P(h|e)=P(h)P(e|h)/P(e);

上述等式右侧分式的分子分母同时除以P(e|h)便得到;

上式表明,当P(h)和P(~h)没有多大变化时,那么e对h的认证度将正相关于P(e|h)/P(e|~h)。如果那个所谓的通灵师不是真正会通灵术,那么他能够预测你将遇到的那个黑人的头发的数目是极不可能的,即通灵师不会通灵术(~h)对预测头发根数(e)的似然性(P(e|~h))基本上可以认为是0,因此P(e|h)/P(e|~h)就非常大,进而P(h|e)/P(h)也就很大,这样意外的证据对于他是通灵师的认证是非常大的。
类似地,我们会发现这样的现象。假如证据e1被证明为真,那么比起类似于e1的证据e2,与e1不同的证据e3对假说的认证度更大,即便是P(h|e2)和P(h|e3)没有区别。那么贝叶斯理论怎么解释这个现象呢?原因是Pi(e2|e1)>>Pi(e3|e1),根据贝叶斯定理我们得到:Pi(h|e2,e1)=Pi(h)/Pi(e1)P(e2|e1),且有 Pi(h|e3,e1)=Pi(h)/Pi(e1)Pi(e3|e1);于是得到 Pi(h|e2,e1)<< Pi(h|e3,e1),即 e3对 e2的认证更大[9]。
贝叶斯认证理论成功地表明,科学家的确会更喜欢惊奇、意外并且是多样化的证据。证据的种类越多,对理论的支持就更大;而证据的意外程度越大,越是不可能,而其对假说的认证也就更大。可见,贝叶斯认证理论与科学实践在这个方面是高度符合的。
四、主观概率与认证度
贝叶斯认证理论之所以优于常规的认证理论在于它不但可以对科学评价做定性的分析,还能导入主观概率并对认证作定量的分析。显然,贝叶斯认证理论的定量研究和概率的主观主义解释是密不可分的。这就回到一个根本的问题,即如何确定主观概率?
按照概率的主观主义解释,概率是主观置信度,那么依托于主观置信度的认证理论也就具有主观性和私人性。如此一来,科学检验和科学认证的客观性如何体现?这正是概率解释的客观主义对贝叶斯主义的最根本的置疑或挑战。这一追问使得贝叶斯认证理论对科学假说所作出的的评价让人生疑,即因人而异的定量的认证理论其量化测度是否是空洞的、苍白的?如果要让这种测度具有客观性和公共性,是否就必须具备概率指派的一般性标准,而一旦提出这种标准是否又同主观概率解释的主旨是相违背?如果贝叶斯理论不能回答这些置疑,那么贝叶斯认证理论作为一种量化的认证理论,在其哲学根基上就失去了重心,让人难以依赖和接受。下面,我们考察贝叶斯认证理论面对这种困境的若干可能出路:
其一,承认主观解释这一基础不可动摇的地位,并且将贝叶斯认证理论置于一种理性的情景下。这里贝叶斯理论是对一个全知全能的理性人的描述,因此概率的指派问题自然就不是问题,一个符合理性的主观置信度必定是融贯且精确的概率。这样认证理论就不需要标准,因为贝叶斯理论只是负责说明这种方法的合理性,而不必太执意于其是否在现实生活中可操作,更不是对困在各种“非理性”思想中的一般人做出描述。
其二,将主观概率进一步扩展为主体间的主观概率。即要深入到具体的知识背景中,对于一个科学事件,决定这个事件的概率的是科学共同体的主观置信度,而科学家之间的主体间性正是能够促成这种达成一致的主观置信度的要素。比如在普劳特事件中,①1815年普劳特提出了一个关于元素原子量的假说,他认为氢原子是基本元素,而所有元素的原子质量都是氢原子质量的整数倍。当时化学家测得的氢的质量是0.125,然而也测得不少元素的原子量不满足普劳特的假说,比如当时测得氯的质量是35.83而不是氢的整数倍,与普劳特的预测不符。不过这些反常当时并没有推翻普劳特的假说,其他科学家比如著名的化学家托马斯(Thomas Thomason)同样也并没有因为反驳证据的出现而怀疑普劳特假说的真实性。参见C.Howson and P.Urbach.Scientific Reasoning.Chicago:Open Court Publishing Company,1993.当时的科学界普遍认为普劳特的假说正确的概率很高,因此该假说的概率可被认定为0.9,这个概率是不以个别科学家为转移的,它体现了整个科学共同体的主观概率,这样我们就能摆脱由于主观概率松散的限制所引发的苛责。而对普劳特假说构成威胁的否证性证据,在当时的背景下实际被赋予的概率是很低的。这也很符合科学家的直觉,即遇到反常时通常怀疑的不是理论本身而是证据的可靠性。
其三,在客观解释的影响下,主观解释向客观解释靠拢退回到一种折中的主观解释,即不再将概率解释为主观置信度,而是将主观概率看做是对客观概率的主观估计。这样既可以减少主观概率的主观性、私人性,从而又可以引入客观概率的客观性。但是这种进路是否能解决主观解释的根本问题而不会引入更多新的问题,是值得进一步思考的。
其四,通过贝叶斯理论的“意见收敛定理”,让初始概率的主观性和私人性淹没在验后概率的客观性和公共性之中,从而达到主观性和客观性的统一。不过,意见收敛定理对“独立重复实验”的要求在科学实践中往往不能完全满足,从而使该定理的有效性受到限制[10]。
限于篇幅,以上的讨论只是初略的,我们这里旨在表明,虽然概率指派的问题对认证理论造成一定的挑战,但这个困难不是根本性的,也并非不可克服的,贝叶斯理论的前景还是颇为乐观的。
五、结束语
从前面的讨论中,我们看到贝叶斯认证理论不仅能够定性地说明证据与假说之间的认证关系,还能通过测度相关性函数定量地描述这种认证关系。这种认证关系并不是单一静态的,而是复合多元的,随着人类认识水平的提高呈现出一幅动态的发展图景。证据的可靠性越低、证据的意外程度越大、证据的多样性程度越高,则证据对假说的支持会越大。随着证据的可靠性不断提升、可重复证据或相似证据逐步积累,证据对假说的认证度会逐渐达到饱和,甚至于到最后完全失去对假说的认证,而此时这些足够丰富、足够准确的证据就会纳入背景知识,或者也被称之为旧证据,从而丧失对假说的认证效应。要想寻求更高程度的认证,科学家就必须诉诸全新的、有着不同经验内容的预测证据来认证假说,这样一种动态的图景如实反映了科学推理的一般特征,也进一步揭示贝叶斯方法的实践意义。然而,贝叶斯认证理论的理论基础是概率的主观主义解释,这里存在一个不容忽视的困境,即如果概率的解释是主观的,这样得来的认证度是否是相对的、因人而异的,如此一来,测得的认证度将会丧失其合理性基础。有显著迹象表明,贝叶斯理论能够在很大程度上克服这一理论困境。
致谢:本文能够顺利完成受益于陈晓平教授的悉心指导与珍贵的修改意见,在这里表示诚挚地感谢。
[1]Huber F.Subjective Probabilities as Basis for Scientific Reasoning?[J].The British Journal for the philosophy of science,2005,56(1):101 -116.
[2]刘治,张端明.贝尔不等式及其实验验证[J].湖北大学学报:自然科学版,2002,24(2):131 -134.
[3]Musgrave A.Popper and“Diminishing Returns from Repeated Tests”[J].Australasian Journal of philosophy,1975(53):248-253.
[4]黎红勤.关于旧证据问题的争论——评豪森的反事实策略[J].重庆理工大学学报:社会科学,2014(3):26-31.
[5]陈晓平,黎红勤.对“老证据问题”的解决[J].自然辩证法通讯,2014(2):26 -30.
[6]Howson C,Urbach P.Scientific Reasoning[M].Chicago:Open Court,1992:120-123.
[7]科林·豪森.定律的逻辑概率一定为0吗?[J].胡浩,译.世界哲学,2012(2):99 -105..
[8]亨普尔.自然科学的哲学[M].张华夏,译.上海:三联书店,1987:66.
[9]Talbott W.Bayesian Epistemology:The Stanford Encyclopedia of Philosophy(Fall 2013 Edition)[DB/OL].[2013-11-12].http://plato.stanford.edu/archives/fall2013/entries/epistemology-bayesian/.
[10]陈晓平.意见收敛定理与休谟问题[J].现代哲学,2008(5):67-74.

