红蓝双方攻防射击决策最优指数策略

李龙跃 刘付显

(空军工程大学 防空反导学院，陕西 西安710051)

1 引言

很多军事作战问题可以抽象为红方防御多个蓝方目标的射击战斗问题，如地空导弹射击多个空中目标的防空作战场景。这种场景下蓝方目标可能有多个类型，红方不能完全确定蓝方目标的类型，且红方也可能被蓝方摧毁而丧失防空射击能力［1］。红蓝双方攻防射击对抗过程本质上是分配红方可用射击资源去射击固定集合的蓝方来袭目标，红方射击策略优劣对射击收益、杀伤蓝方目标数量和红方生存概率都有影响，因此红方制定和选用最优射击策略对于获取最高射击收益至关重要。Gittins 和Jones 首先基于指数最大化来研究决策问题［2］。近年来，Christopher M. Anderson［3］、Gu M Z［4］、Isaac M Sonin［5］、U Dinesh Kumar［6］、Si P B［7］等对Gittins 指数理论研究及在资源调度、任务分配和随机决策等领域的应用进行了拓展，Glazebrook 和Gaver 结合Gittins 指数讨论了军事射击优化问题［8］。本文通过引入和拓展指数策略(Index Policy)应用于红蓝双方攻防射击问题，以红方在自身被摧毁之前最大化杀伤蓝方目标的收益(或数量)为目标，对指数策略在射击策略中的最优性进行了讨论，旨在最大化红方作战收益，对于辅助红方射击决策和建设作战指挥信息系统具有一定借鉴意义。

2 红蓝攻防射击的马尔可夫过程描述

首先考虑1 个红方火力单元射击N个蓝方目标的问题，规定“1 次战斗”至少包括红方对蓝方进行1 次射击(期间红方有可能被蓝方摧毁)，也包括红方对蓝方目标杀伤效果的观察过程。假设防空武器系统的弹药数量不受限制，此时红方的核心决策问题在于如何根据以往的射击战斗情况，选择下一个需要射击的目标，从而最大化射击过程中的期望收益。以上决策问题可以描述为马尔可夫决策过程［11］:

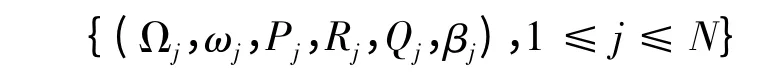
(1)X(t)={X1(t)，X2(t)，…，XN(t)}表示t∈N时刻(即在t +1 时刻之前)蓝方目标的状态集合，Xj(t)表示蓝方目标j的状态。

(2)Xj(t)∈Ωj∪{ωj}，其中Ωj是红方对蓝方目标j所有可能状态的认知空间，Xj(t)=ωj表示在时刻t，红方被蓝方目标j摧毁。

(3)在t∈N时刻，aj表示在红方没有被摧毁的前提下，选择下一次射击(即在t +1 时刻)蓝方目标j。

(4)红方在t∈N时刻采取射击行动aj的期望收益为有界且非负函数:

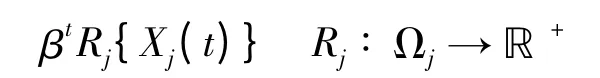
常数β 为折扣因子，Rj可以理解为蓝方目标j的价值或对红方造成的威胁值。

(5)Qj为标记函数，满足:

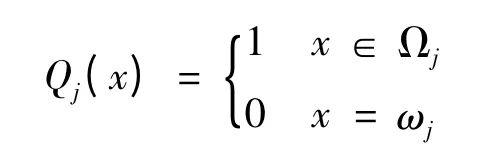
标记函数Qj(x)=0 表明如果红方被摧毁则红方收益为0，下一时刻停止射击或目标飞出射击时间窗口。

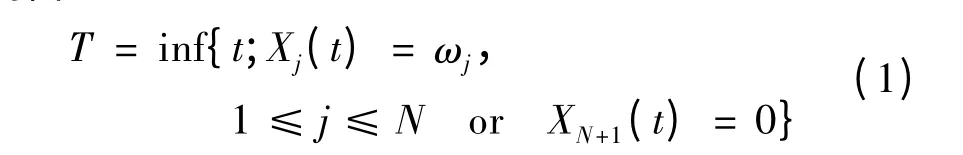
(6)如果红方在t时刻执行射击行动aj，蓝方目标j状态由Xj(t)变为Xj(t +1)的概率为:

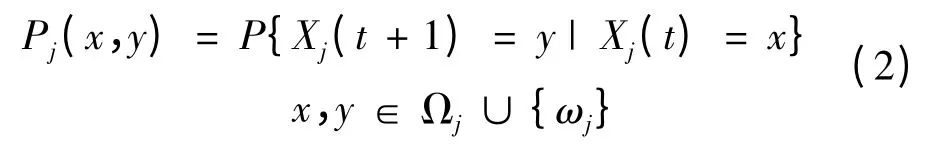
显然Ωj包含状态¯ωj，表示蓝方目标被杀伤而红方未被摧毁。为描述射击行动的期望收益，引入有界函数:

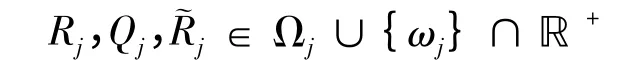
其中Rj(x)表示在时刻t红方执行行动aj的期望收益函数，˜Rj = RjQj，则红方在时刻t执行射击行动aj的期望收益为:

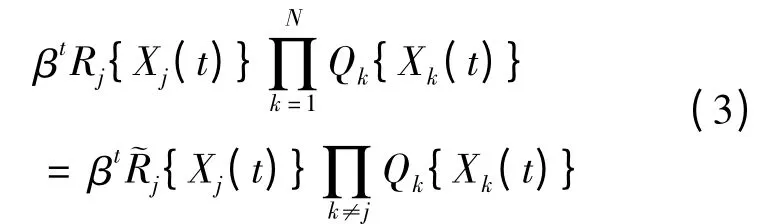
从式(3)中的Qk乘积项也可以看出如果红方在射击过程中被摧毁则收益为0，引入折扣因子β∈(0，1)来增加模型的通用性，β 的取值一般由决策者自行设定［12］。

3 指数射击策略

一个射击策略本质是红方基于历史射击效果，决策每一时刻射击蓝方目标行动的一种规则。设射击策略为v，v(t)表示时刻t红方的射击选择，则策略v下射击期望收益为:

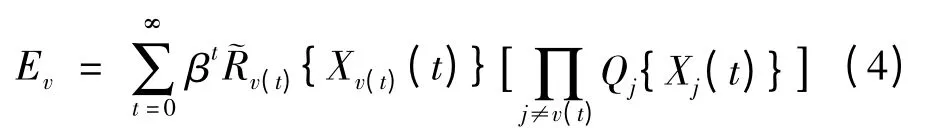
研究射击策略的目的在于找到最优射击策略v*，使得红方射击期望收益最大。上述分析是马尔可夫决策过程的一种，叫作广义bandits 决策过程。广义bandits 决策过程在不同决策行为之间引入了相互独立的决策收益，可以作为研究射击问题的框架。

令τ 表示红方射击过程结束时刻，˜Rj(x，τ)表示在时间段［0，τ)红方的射击期望收益，则:

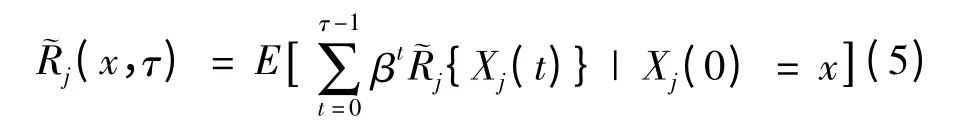
当红方被摧毁时，则红方收益也被终止，其收益率为:

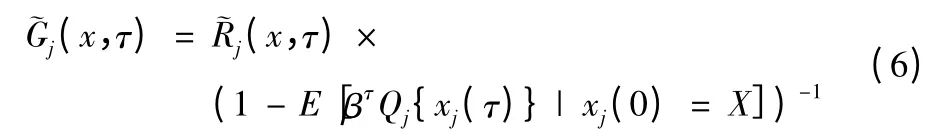
Gj(x)为˜Gj(x，τ)最大值。文献［13］探讨过Gj(x)的计算方法。

对于广义bandits 决策过程存在最优射击策略，有定理1。

定理1［14］存在函数Gj∶Ωj→ℝ+，假设在时刻t红方未被摧毁，红方射击蓝方目标j*是最优策略，当且仅当j*满足下式:

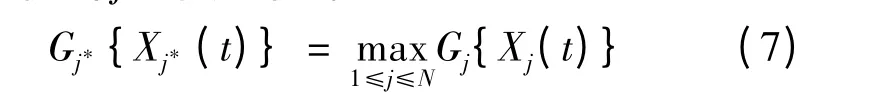
假设蓝方目标有B种类型，“类型”是指随着射击战斗进行，可以决定射击结果的蓝方目标特征的总称。这里设定目标“类型”是为了增强方法的普遍性，因此“类型”是广义的，需要根据具体问题进行设定，其常用的区分方法可以是依据对目标的不同杀伤概率进行划分，如在防空作战中“类型”可以是不同类型的目标，如隐身目标、轰炸机目标、战斗机目标等。通常情况下红方不能确定蓝方目标的类型，射击前其不确定性由N个独立先验分布∏1，∏2，…，∏N表示，∏j b表示红方判定蓝方目标j属于b类型的概率(1 ≤j≤N，1 ≤b≤B)。设在1次战斗中，所有射击结果相互独立，红方对蓝方b类型目标的杀伤概率为rb，被其摧毁的概率为θb。红方在第t次射击杀伤一个蓝方b类型目标的收益为βtRb，红方的战斗目标是在被摧毁前最大化杀伤蓝方目标所获得的收益(若β=1，Rb =1，红方的战斗目标等价于在被摧毁前最大化杀伤蓝方目标的数量)。基于贝叶斯理论，在经历n次战斗后，如果红方和蓝方目标j均存活，则此时红方判定蓝方目标j属于b类型的概率可由后验分布∏j，nb来表示:

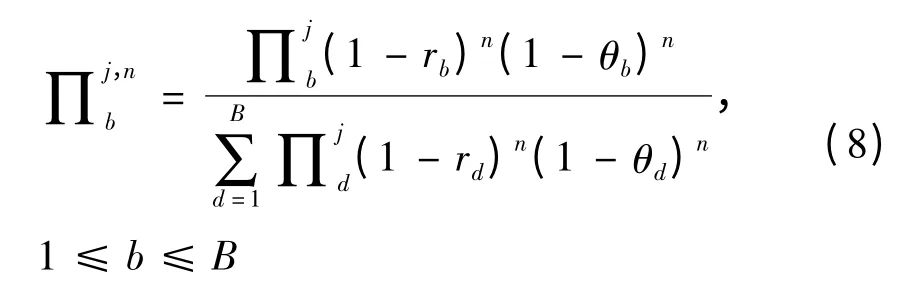
则可得到下式:

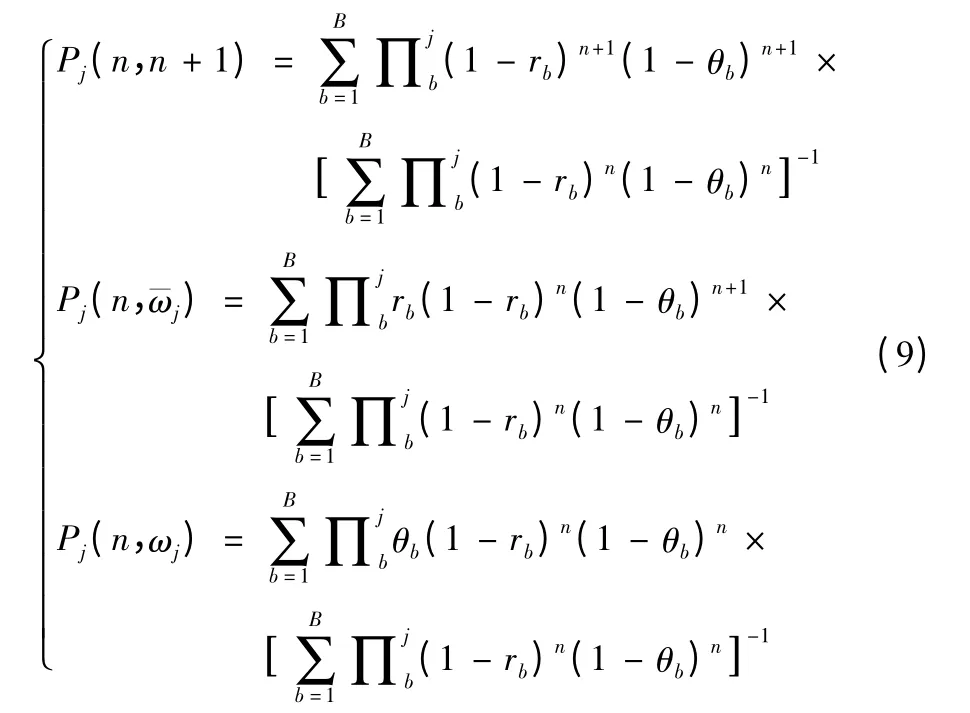
式(9)中的3 个式子分别表示红方和蓝方目标j均存活、红方存活且蓝方目标j被杀伤和红方被摧毁三种情况。三种情况下射击行动的期望收益(不带折扣因子)为:

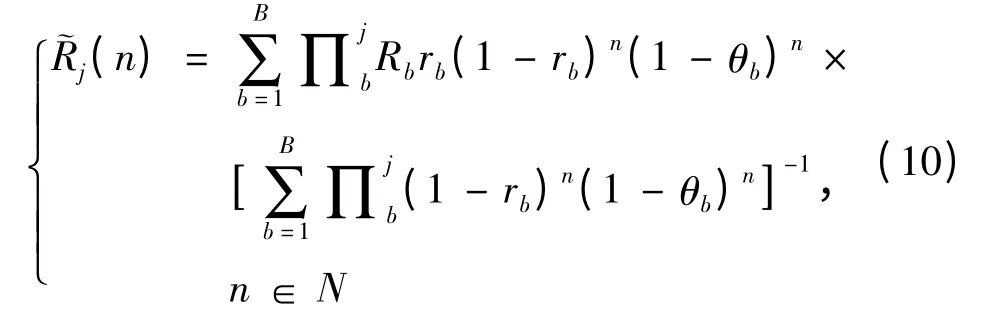
令随机变量τr为红方射击的终止时刻(r为正整数，Xj(0)= n)，红方对蓝方目标j能射击r次，直到两者之间有一个被摧毁时停止射击。τr表示当前红方射击次数，则红方射击行动的期望收益为:

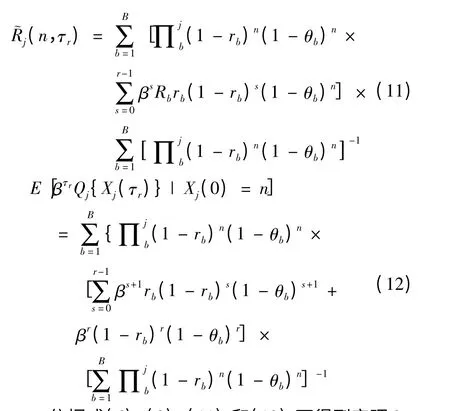
依据式(6)、(8)、(11)和(12)可得到定理2。

定理2 假设在时刻t红方未被摧毁，红方射击蓝方目标j*是最优策略(Xj*(t)≠¯ωj*)，当且仅当j*满足下式:

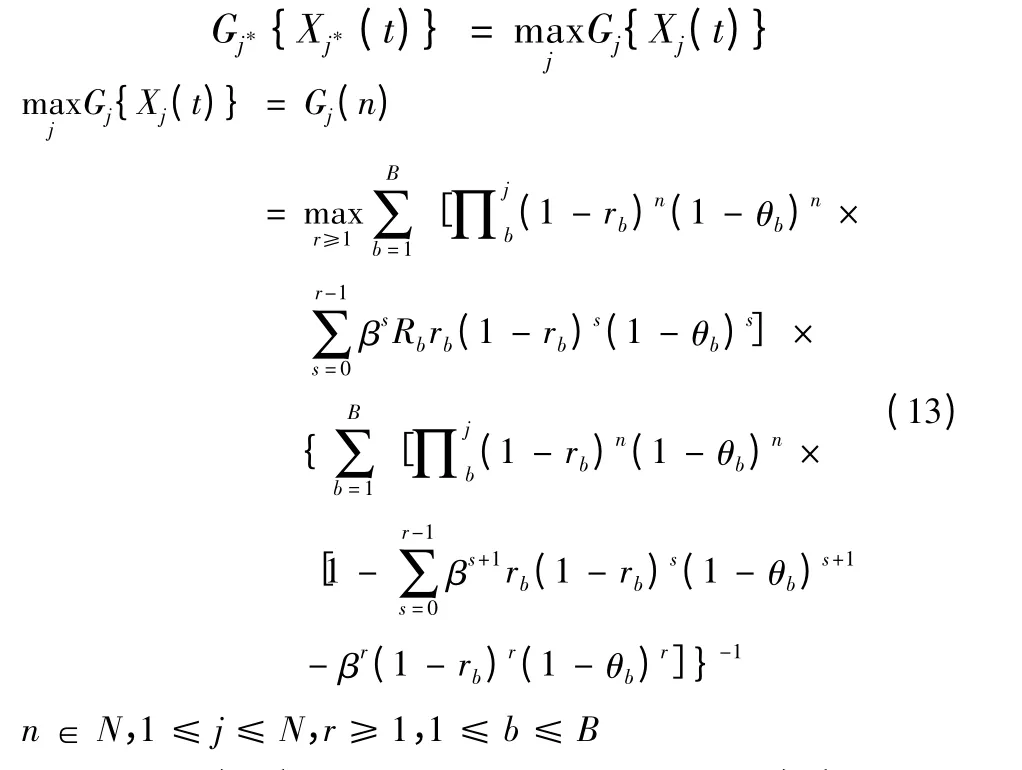
令式(13)中r =1，则可将Gj(n)化为Hj(n)(即仅考虑当前射击收益，不考虑后续射击收益)。

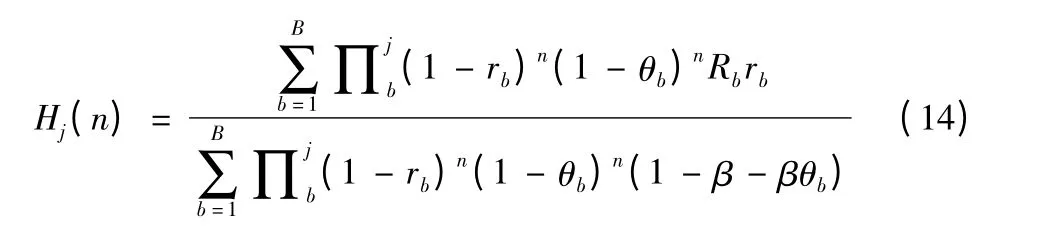
式(14)中Hj(n)本质上可以被理解为红方射击蓝方b类型目标的加权平均收益指数Rbrb(1-β+βθb)-1。当Rb和rb较大，θb较小时射击收益指数较高，即目标价值和红方杀伤蓝方概率较大，被蓝方摧毁概率较小时收益指数较高，射击收益较高，此目标适宜射击;反之，对于Rb和rb较小，θb较大的目标，即目标价值和红方杀伤蓝方概率较小，被蓝方摧毁概率较大时收益较低，此目标不适宜射击，上述结论较为符合实际作战认知。

如果函数Hj(n)是单调递减的，则对于所有n当r =1 时式(13)取得最大值，此时有Gj(n)=Hj(n)。这种特殊情况表示红方的射击策略是不停转换所需射击的蓝方目标，选择射击指数最高的目标射击。如果函数Hj(n)是单调递增的，则对于所有n当r→∞式(13)取得最大值，此时Gj(n)为:

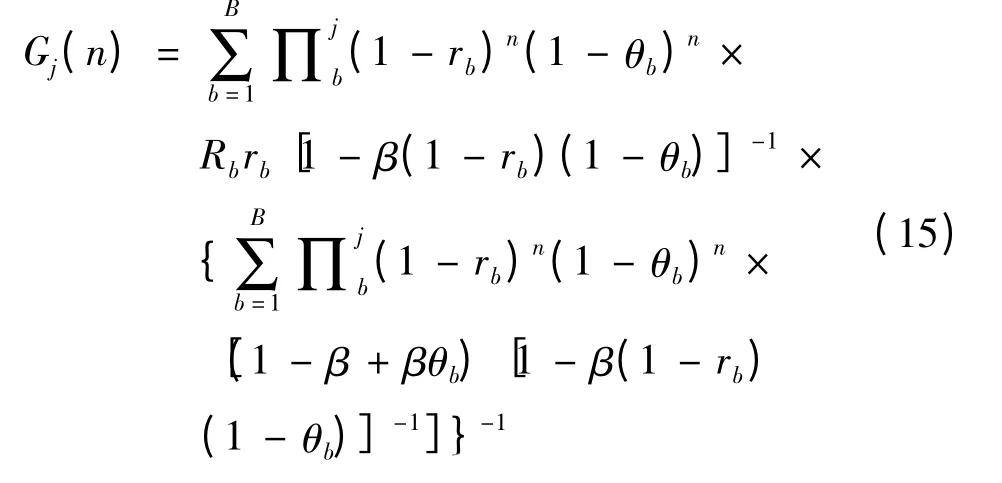
这种特殊情况表示红方最优策略是对每一个蓝方目标持续射击直至目标被杀伤。

4 近视策略、随机策略和循环策略

为了和指数策略进行比较，给出近视策略(Myopic Policy)、随机策略(Random Policy)和循环策略(Round - Robin Policy)3 种射击策略。

(1)近视策略。如果指数策略选择射击目标是考虑射击战斗的长远期望收益，那么近视策略选择射击目标则是考虑即时最优收益，因此近视策略又可称为即时最优策略。近视策略指导红方决策者按“眼前”最优收益进行射击。如果蓝方目标j为b类型的先验概率分布为∏j b，采用近视射击策略，进行n次射击战斗后收益为:

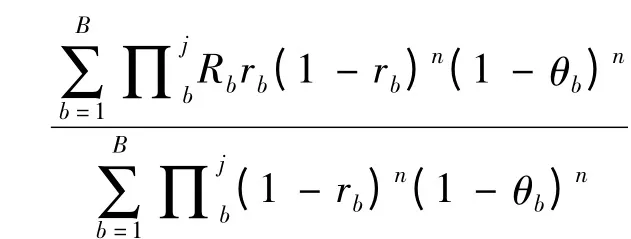
近视策略并不一定是最优策略［12］。举例说明，如某次射击战斗，有2 枚射击弹，射击2 个目标，2 枚射击弹对2 个目标的杀伤概率是［1，0.9;0.9，0］，R1= R2=1。按照近视策略，用第1 枚选择目标1，不使用第2 枚射击弹，总收益是1，而最优的策略则是用第2 枚射击目标1，如果失败再用第1 枚射击目标1，或者第1 枚射击目标2，总收益都是0.9×(1+0.9)+0.1×(0+1)=1.81，显然这说明了近视策略并非最优策略。对本文研究来说，近视策略以红方当前时刻收益最大为目标，计算量小，实时性强，但未考虑下一时刻目标类型的变化对射击收益的影响，适用常规目标无差别射击。

(2)随机策略。随机射击策略就是对存活待射击的蓝方目标，红方从中随机选择进行射击，选择任何一个蓝方目标的概率相等或相似。

(3)循环策略。循环射击策略就是对存活待射击的蓝方目标，红方按某种顺序循环射击，其中，第1 个射击目标随机选择决定。

5 实例分析

参数设置:设计2 个射击战斗场景，均含有10个待射击蓝方目标，蓝方目标有5 种类型，具体参数见表1。从表1 中可以发现基本上蓝方价值越高的目标就越难被杀伤，并且红方被摧毁的概率越大。已知N =10，B =5，每次计算将目标分成5 组，设置组内第i类型目标先验概率为0.75，组间则设相互独立，并服从U(0，1)分布，满足1(1 ≤j≤10)，折扣率β 设置为0.95。

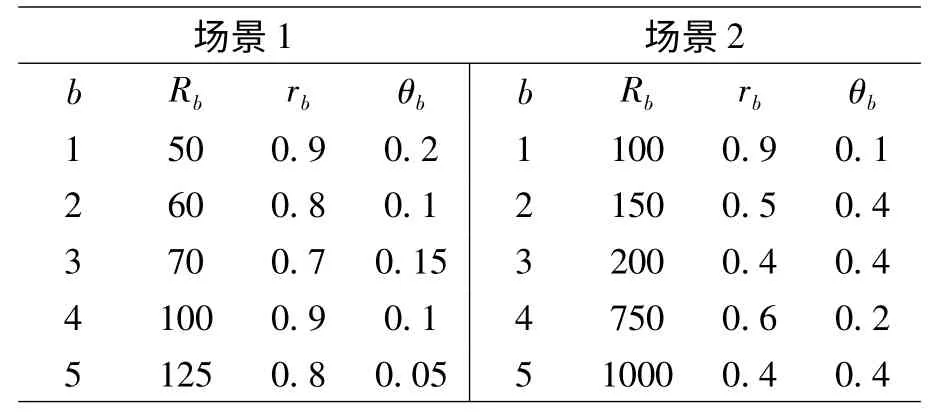
表1 红蓝双方参数值

实验过程:用4 种射击策略对2 个场景问题进行求解，针对4 种射击策略分别计算10000 次。

实验结果:实验记录了2 个场景红方的收益，包括最小收益、平均收益、最大收益、平均杀伤数量、红方被摧毁概率等数据。表2 是2 个场景下针对4 种射击策略红方收益数据，表3 是2 个场景下针对4 种射击策略红方杀伤蓝方目标数量数据，表4 是4种射击策略下红方被摧毁的概率。

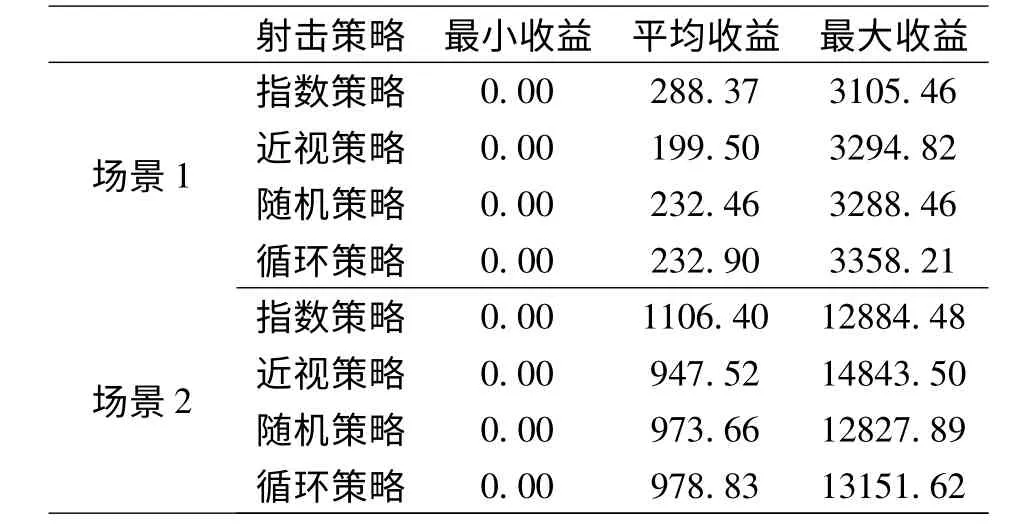
表2 红方收益数据

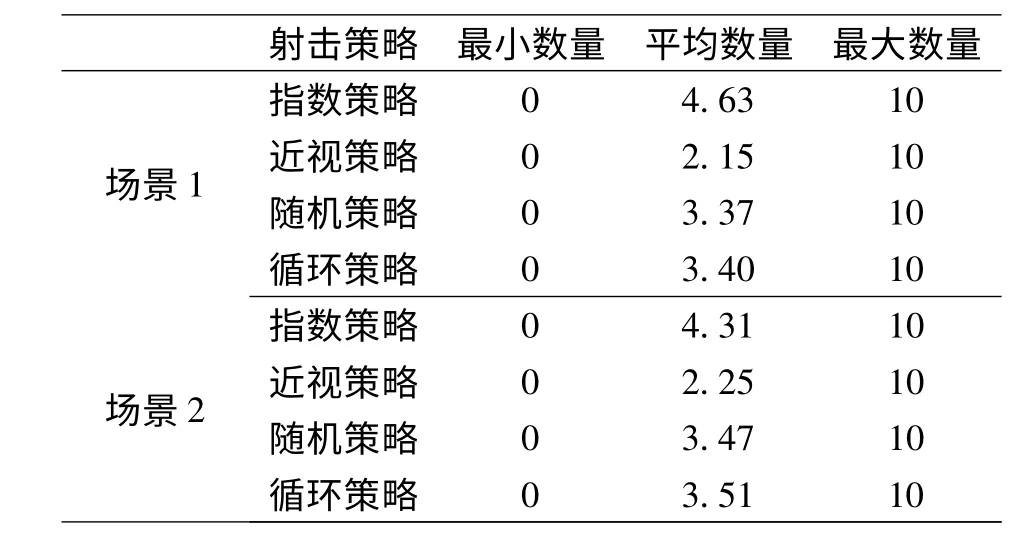
表3 红方杀伤蓝方目标数量数据

表4 红方被摧毁的概率

6 结论

一般认为，射击战斗过程中较好射击策略是根据红蓝双方当时状态确定的，应当是即时最优策略(近视策略);较差策略是随机策略，因为随机策略不考虑射击收益，而通过实例和计算结果分析发现并非如此。4 种射击策略中指数策略要优于其他3种射击策略，尤其是平均射击总收益和平均杀伤蓝方目标数量上具有优势，与定理1 和定理2 的论述相符。近视策略比预想表现要差，其根本原因在于对红方自身被摧毁的概率考虑较少，导致红方较早被摧毁而结束战斗，获得的射击总收益也较少。实例中，近视策略甚至还不如随机策略或循环策略，其原因有待下一步研究。

［1］ 武从猛，王公宝.大型水面舰艇编队空中来袭目标威胁值评估［J］.军事运筹与系统工程，2013，27(3):24 -27.

［2］ GITTINS J C. Multi-armed bandit allocation indices［M］. Chichester:Wiley，1989.

［3］ CHRISTOPHER M ANDERSON. Ambiguity aversion in multi -armed bandit problems［J］. Theory and Decision，2012，72(1):15 -33.

［4］ GU M Z，LU X W. The expected asymptotical ratio for preemptive stochastic online problem ［J］. Theoretical Computer Science，2013，49(5):96 -112.

［5］ ISAAS M SONIN. A generalized Gittins index for a Markov chain and its recursive calculation［J］. Statistics and Probability Letters，2008，78(12):1526 -1553.

［6］ U DINESH KUMAR，HARITHA SARANGA. Optimal selection of obsolescence mitigation strategies using a restless bandit model［J］. European Journal of Operational Research，2010，200(1):170 -180.

［7］ SI P B，JI H，YU F R. Optimal network selection in heterogeneous wireless multimedia networks ［J］. Wireless Networks，2010，16(5):1277 -1288.

［8］ GLAZEBROOK K D，GAVER D P，JACOBS P A. On a military scheduling problem ［R］. Monterey CA:Naval Postgraduate School，2001.

［9］ BARKDOLL T C，GAVER D P，GLAZEBROOK K D，et al.Suppression of enemy air defense(SEAD)as an information duel［D］. Monterey: Naval Postgraduate School Working Paper，2001.

［10］ GLAZEBROOK K D，WASHBURN A. Shoot - Look - Shoot:A review and extension ［J］. Operations Research，2004，52(3):454 -463.

［11］ GLAZEBROOK K D，MITCHELL H M，GAVER D P，et al.The analysis of shooting problems via generalized bandits［R］.Monterey CA:Naval Postgraduate School，2004.

［12］ GLAZEBROOK K D，KIRBRIDE C，MITCHELL H M，et al.Index policies for shooting problems［R］. Monterey CA:Naval Postgraduate School，2006.

［13］ GLAZEBROOK K D，GREATRIX S. On transforming an index for generalized bandit problems［J］. Journal of Applied Probability，1995，32(1):168 -182.

［14］ NASH P. A generalized bandit problem［J］. Journal of the Royal Statistical Society (Series B)，1980，42(2):165 -169.