基于特大齿轮在位测量姿态调整系统的调平算法的仿真研究

范成功 吕 强 陈西曲 陈光辉

（武汉轻工大学 电器与电子工程学院，湖北 武汉 430023）

0 引言

在现代制造、高精度测量、军用以及民用生产制造等各技术领域，都存在姿态调整这一概念。姿态调整指的是将某些设备或仪器精确地调整到指定角度和位置，以提高整个系统的稳定性和精度特性，满足某些特定的技术指标。在大型齿轮测量领域中，无论是台式仪器测量还是在机式测量，都必须对被测齿轮或者量仪进行定位，也就是调整齿轮与量仪之间的空间位置，这是保证测量精度的首要前提[1]。对于台式仪器而言，由于量仪精度高、测量条件好、定位精确，由定位误差而导致的测量误差被无形地消除和减小[2]。

在以往的大齿轮测量中，定位方式一般是用齿顶、齿槽、三球、公切线来定位，借助辅助基准面、定位机构等实现。本文涉及的基于激光跟踪测量的特大型齿轮在位测量系统中的姿态调整指的是如何根据齿轮的位置，对三维测量平台进行精确的定位，调整三维平台的姿态，满足系统的高精度定位要求。从基于激光跟踪技术的大型齿轮测量方法中可知，系统在每一次测量开始前，都必须要先调整三维测量平台姿态，这也是在位测量系统的关键技术之一。

1 姿态调整系统

常用的姿态调整方式有基于三点或多点支承式调整，多联杆式调整，多轴并联式调整，链条链轮式调整等多种方式。本文涉及的姿态调整系统采用三点支承式调整，其原理方案为：A 轴、B 轴、E 轴3 个与步进电机相联的机械支承轴用来支撑姿态调整平台上端面，并根据控制指令升高或降低，来改变平台上端面的空间位置；Z 轴1 个与步进电机相联的旋转齿轮与平台底部啮合，并根据控制指令旋转角度，以改变三维测量平台的测量臂在水平面内的方向。

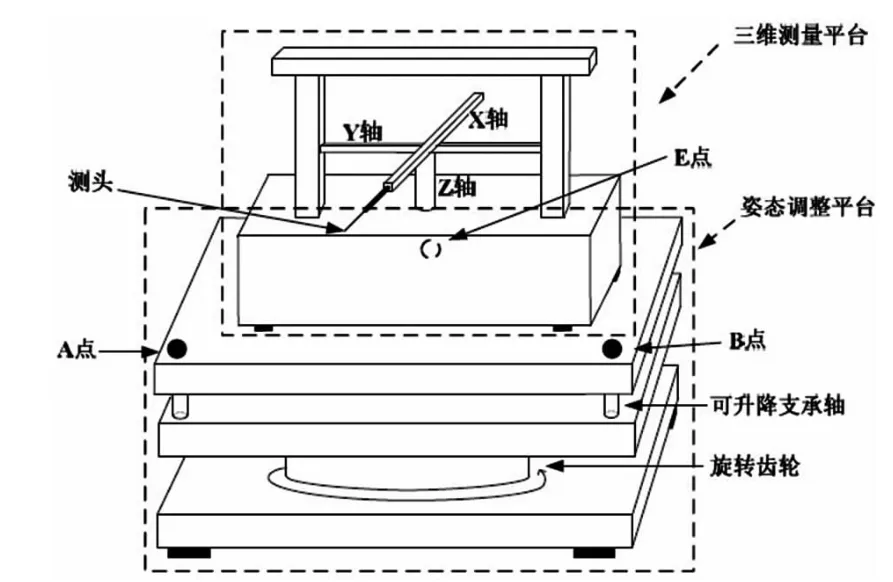
图1 姿态调整平台及三维测量平台

2 姿态调整系统调平算法的设计

为了实现对特大齿轮在位测量系统的精确调整和精准控制，根据系统的总体要求设计了姿态调整系统的相关算法[3]，并将算法转换为了可以实现的源代码，以便完成对系统的良好的控制[4]。算法所需要的数据是来自于经过处理的激光跟踪仪测量的数据，此数据用于完成算法数据的输入。算法最终所要达到的效果是实现对于被测量的特大齿轮的上端平面的法向量与三维平台的法向量相平行，以便实现后续的对特大齿轮各项参数的测量。

算法的具体实现过程是将被测工件即特大齿轮的端平面的法向量向三位平台的法向量上投影，主要是分解齿轮的法相量中的 到三维平台的坐标系中。算法的实现示意图如图2 所示。

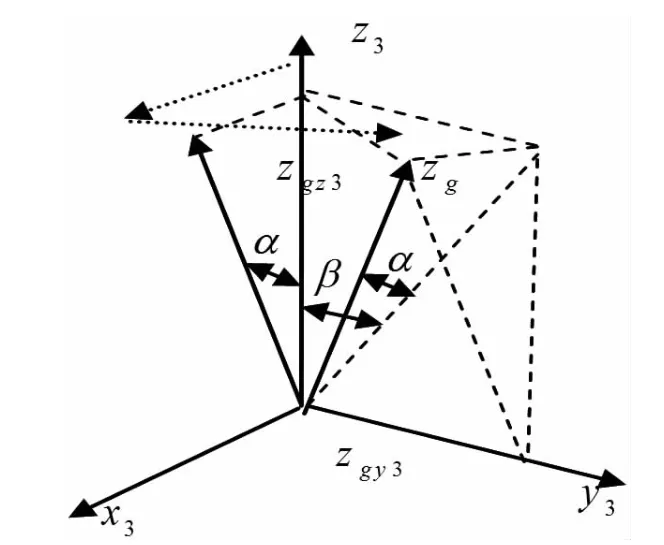
图2 系统调整算法空间结构示意图

算法详细描述，首先建立如图1 所示的坐标系x3，y3，z3表示三维平台的空间坐标系统。图中的zg表示工件的坐标的z3方向分量即要测量的特大齿轮的z3方向向量。然后分别将特大齿轮的z3方向向量zg分别在xoy 平面上的y 轴和yoz 平面上z 轴进行投影，通过计算得到相应的夹角α 和β，只要将三维平台围绕着x3轴旋转β 角度，然后再绕着y3轴旋转α 角度就可以完成调平的过程。zg在y3轴的投影

同理可求出zg在z3的投影zgy3为：

将zg绕x3旋转β，再绕y 旋转α 即可使zg与z3重合。实际调整过程中只要将三维平台先绕y3旋转α 然后绕x3旋转β 角即可完成相应的调整过程。

表1 三维平台的方向向量和工件方向向量的数据

3 调平算法的MATLAB 仿真与分析

实验步骤：

（1）将激光跟踪仪采集到的数据保存文本文档里。

激光跟踪仪测量获取的三维平台的方向向量和工件方向向量的数据见表1。

（2）Matlab 软件读取文本数据。

（3）Matlab 软件执行相应的姿态调整的旋转矩阵和旋转方向判断的代码。

（4）显示调整前和调整后的三维平台的法向量和工件法向量的夹角。

实验结果：

实验结果分析：

调整前三维平台的法向量和工件的法向量的夹角：2.441634251473566。

调整后三维平台的法向量和工件的法向量的夹角的理论值：0.001078456711702。

调整后三维平台的法向量和工件的法向量的夹角小于0.005 度满足测量精度要求。

调整后三维平台的法向量和工件的法向量的夹角的理论值0.001078456711702＜0.005 满足要求，因此姿态调整系统按照该调平算法调整后的结果比较理想。

4 总结

本文对特大齿轮在位测量的三维平台调整系统的调平算法进行了仿真研究，用MATLAB 软件采用激光跟踪仪测到的数据对姿态调整系统的调平算法进行了理论验证，取得了满足实际精度要求的结果，对特大齿轮在位测量的三维平台调整系统的正常运行具有重要意义。由于受实际系统的机械结构形式等限制，其实际调整后的角度与理论值会有一定的误差，但这也为深入研究姿态调整系统的其它调平方法提供了一定的借鉴和参考。

［1］Shi Zhaoyao，Zhu Lianqing.A Generalized Model of Deviations of Complex Curved Surfaces[J].Proceedings of ISPMM 2004:50-51.

［2］R.Klette，K.Schluns and A.Koschan.Computer vision:Three-dimensional data from images[D].SpringerVerlag:Singapore，1998.

［3］王颖，刘杰，张星.三支撑平台自动调平算法研究[J].科学技术与工程，2011，2.

［4］史厚强.基于三点支撑的仪器调平[J].仪器仪表学报，2004；25(4).