CFRP索斜拉-悬吊协作体系桥的动力特性及地震响应分析

刘荣桂，陈 蓓，冯国英，蔡东升

(江苏大学土木工程与力学学院，江苏镇江212013)

碳纤维增强复合材料(carbon fiber reinforced plastics，CFRP)具有轻质、高强、耐腐蚀、抗疲劳等优良性能，将其用作大跨度桥梁的缆索，可以提高结构的承载效率及跨越能力，规避传统钢缆索易锈蚀易疲劳的问题［1-2］.斜拉-悬吊协作体系桥作为一种比较新型的缆索承重体系桥梁，通过斜拉桥与悬索桥结构的相互协作，实现了两种桥型的优势互补.相对于悬索桥，斜拉部分的存在提高了整桥的刚度，减轻了主缆及锚碇的负担;相对于斜拉桥，悬索部分的存在减轻了主梁及主塔的负担，同时施工过程中的抗风稳定性也有所提高［3-4］.目前，对于CFRP索斜拉-悬吊协作体系桥动力特性及地震响应方面的研究还较为鲜见.本课题组对CFRP索斜拉桥的静动力性能以及CFRP索斜拉-悬吊协作体系桥的静力性能进行了前期研究［5-7］，在此基础上，本研究参考某大桥斜拉-悬吊协作体系桥方案，建立该桥的斜拉-悬吊协作体系桥的动力计算模型，并按照等轴向刚度原则，用CFRP索替换传统钢拉索，采用非线性有限元动力分析的方法，研究CFRP索斜拉-悬吊协作体系桥的动力特性及地震响应，并与相同结构布置形式的钢索桥进行对比，以为该类桥梁的设计及应用提供参考.

1 计算理论

相对于静力理论和反应谱理论，采用直接动力分析理论能够更加真实地反应结构在地震作用下的响应.本研究依据地震作用的直接动力分析理论，采用地震反应的动态时程分析方法，对上述模型进行三维地震响应分析.首先选择合适的地震波输入，采用三维有限元动力计算模型建立地震动方程，然后采用New-mark-β法进行逐步数值积分，并对方程求解.地震作用下，单自由度体系的运动方程可表示为

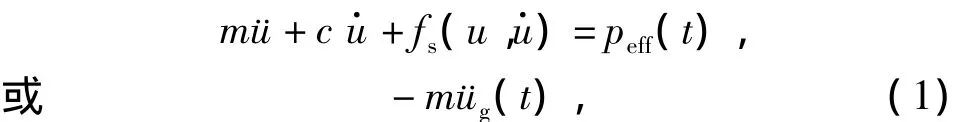
式中:m，c分别为质量和阻尼;fs为恢复力;peff(t)为地震作用的时间函数;u，u·和¨u分别为位移、速度和加速度的时间函数.

离散求解时间段，则离散的时间点ti时刻的运动方程为

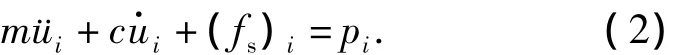
根据New-mark-β数值积分方法，后一时刻的地震反应值可以用前一时刻的地震反应值(速度、加速度及位移)来表示，最后代入式(1)逐个计算.t+Δt时刻的速度和位移可表示为

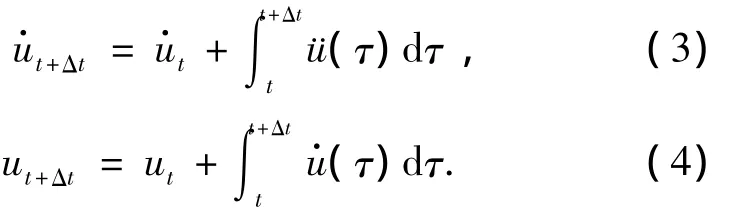
2 试验

本研究利用国内首座CFRP索斜拉试验桥—江苏大学人行天桥(图1)进行了整桥结构的动态特性测试研究，得到了该CFRP索斜拉桥结构的相关自振特性(见表1).

图1 江苏大学CFRP索斜拉试验桥

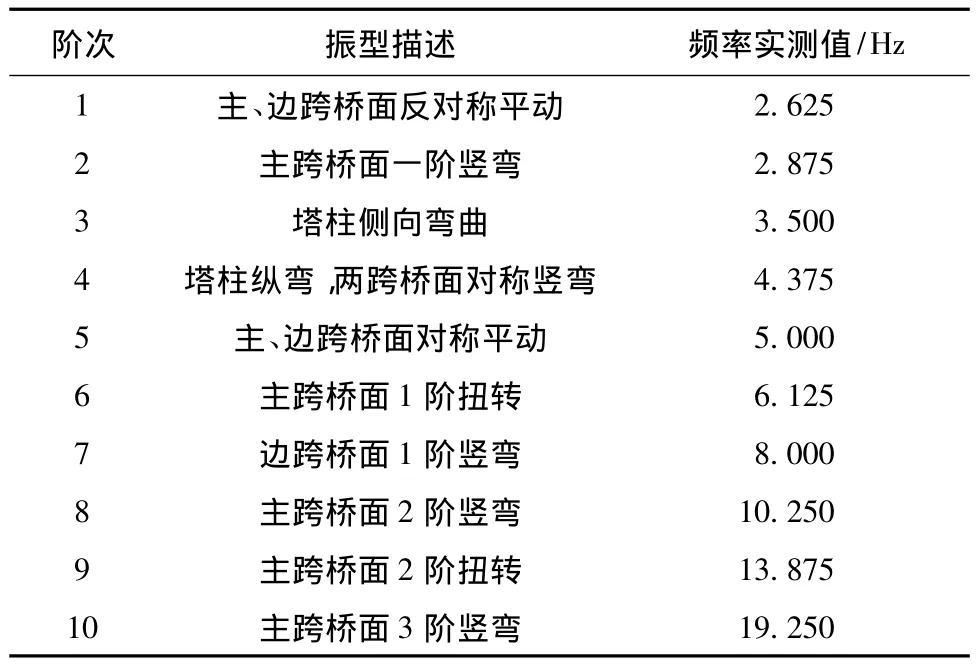
表1 CFRP索斜拉试验桥动态测试结果

该CFRP索斜拉试验桥本身跨度较小而刚度较大，因此，其自振频率较大而自振周期较短，频率分布比较均匀.与同跨度的钢索斜拉桥的自振特性进行对比，分析结果表明，CFRP索斜拉桥的自振频率高于钢索斜拉桥，有利于结构抵抗低频激励［8］.由于试验桥本身刚度较大而跨度较小，故CFRP索对于结构自振频率的提高作用不是十分明显.但可以推测，随着跨度增加这种作用将更加明显.

3 计算模型

根据试验桥动态测试结果，笔者结合某大桥斜拉-悬吊协作体系方案［9］，拟定了一座相同跨径布置的地锚式斜拉-悬吊协作体系桥(见图2):具体跨径布置为260+800+260=1 320 m，边跨各设置2个桥墩;主塔采用H型双塔柱，主梁采用流线型钢箱梁;按照索的等轴向刚度的原则将传统钢索替换为CFRP索;具体结构及构件参数参见文献［9］.索的等强度和等轴向刚度替换，是指在其余设计参数相同的情况下，钢索斜拉-悬吊协作体系桥中，采用CFRP索替换传统钢索，索的截面积分别按下列公式计算:

图2 主跨800 m斜拉-悬吊协作体系桥结构布置图

等强度原则:

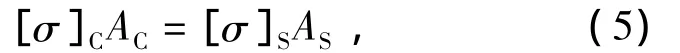
等刚度原则:

式中:［σ］C和［σ］S分别为 CFRP索和钢索的容许应力;AC和AS分别为CFRP索和钢索截面积;EC和ES分别为CFRP索和钢索的弹性模量.

本研究采用Ansys有限元软件，建立了全桥结构的动力分析模型，如图3所示(单位:m).其中，主梁及主塔采用 BEAM189单元模拟，横梁采用BEAM4单元模拟，主缆、吊杆及斜拉索采用LINK10单元模拟.缆索和主梁通过横梁连接，横梁处理为刚性，通过设置主从节点的方式将缆索约束到主梁相应位置.全桥采用半漂浮结构体系，主梁与主塔之间仅设置竖向支座，主梁与边墩之间只约束横桥向及竖桥向位移.

图3 结构动力分析的有限元模型

塔、墩底部约束采用基础等效刚度输入方法模拟［10］，即采用边界单元模式来模拟塔墩底的桩土共同作用，如图4所示.其中K1，K2，K3分别表示各墩台z，y，x方向上拉压弹簧等效刚度系数;K4，K5，K6分别表示各墩台z，y，x方向上抗扭弹簧等效刚度系数.

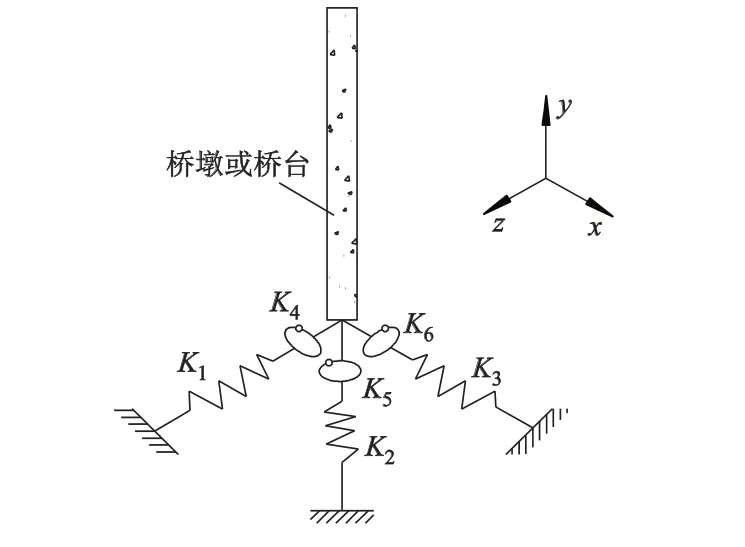
图4 墩台边界约束模式

4 结果及分析

4.1 动力特性分析

对CFRP索斜拉-悬吊协作体系桥和传统钢索桥进行全桥模态分析，采用兰索斯(Block Lanczos)模态提取法提取前100阶振型.主跨800 m的CFRP索桥及钢索桥自振特性分析结果见表2.图5为2种索斜拉-悬吊协作体系桥前19阶振型的频率对比.

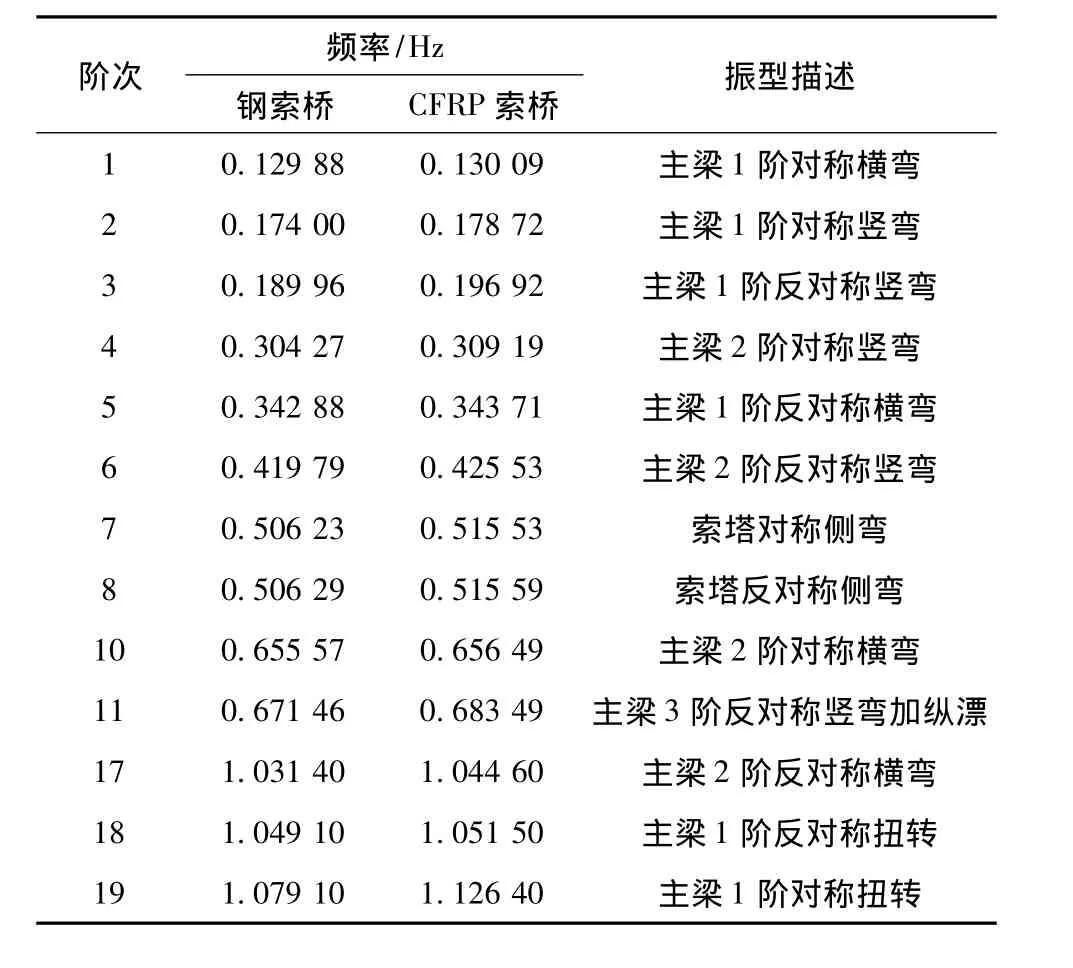
表2 2种索桥频率及振型计算结果

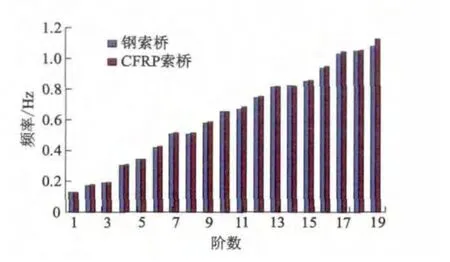
图5 2种索桥的前19阶频率对比

结合图表可以看出:大跨度斜拉-悬吊协作体系桥的自振周期较长、频率分布比较密集，各阶振型表现出明显的三维性及相互耦合等特点;其1阶扭转频率较大，且伴有其他振型的耦合成分，表现为塔、梁、索共同参振;采用等轴向刚度原则换索时，两种桥的前19阶振型基本相似，但CFRP索桥的各阶自振频率较钢索桥有一定提高.说明CFRP索对桥身整体刚度有较好提高作用，有利于大跨度斜拉-悬吊协作体系桥结构抵抗低频激励.

4.2 地震响应分析

4.2.1 地震波输入

地震波以加速度时程的形式输入，方向为沿桥纵向+竖向输入.本桥基本周期约为7.7 s，而地震波持时一般取为结构基本周期的5～10倍，故地震波持时取100 s.纵桥向及竖桥向地震波加速度时程曲线见图6.

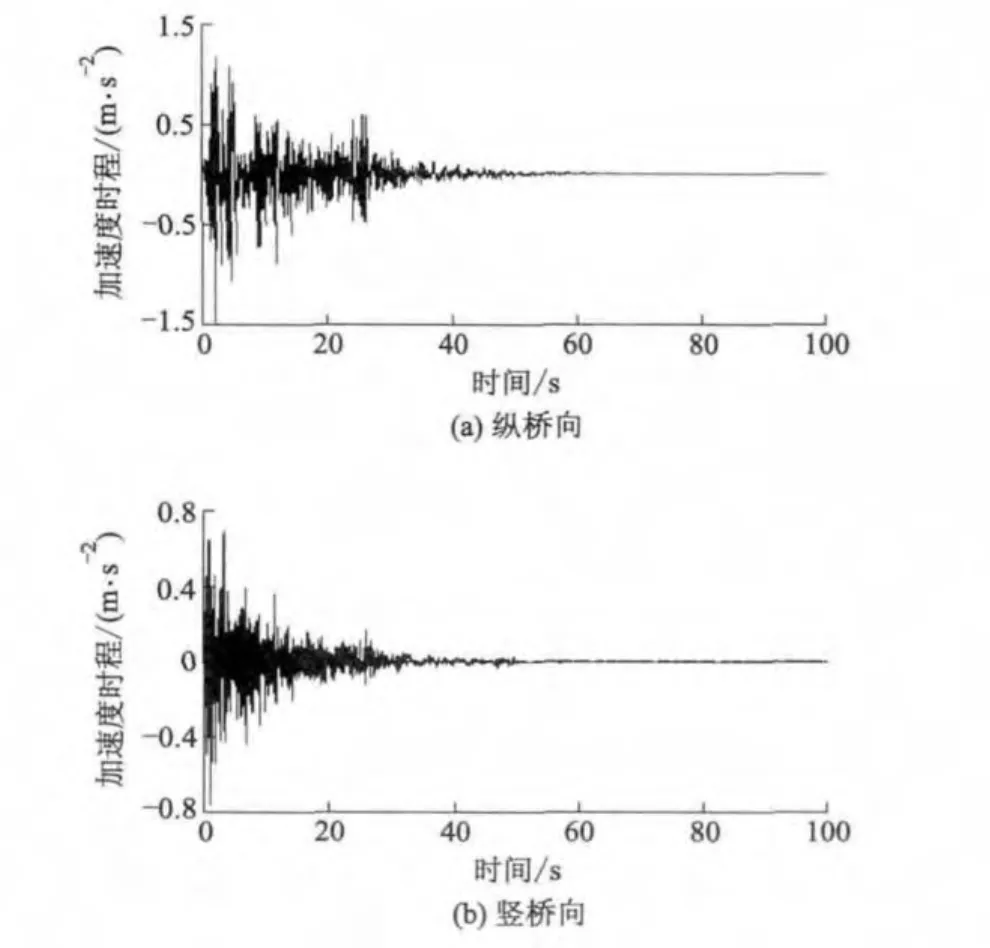
图6 地震波加速度时程

4.2.2 地震响应时程分析

1)主梁地震响应时程.图7为CFRP索和钢索桥主跨跨中位移时程图.由图7a可知:CFRP索桥的竖桥向位移在大部分时刻小于对应钢索桥的竖向位移，且CFRP索桥竖向位移响应的衰减速度较钢索桥快.由图7b可知:对于相同结构布置形式的2种索桥，主跨跨中纵桥向位移响应比较接近.

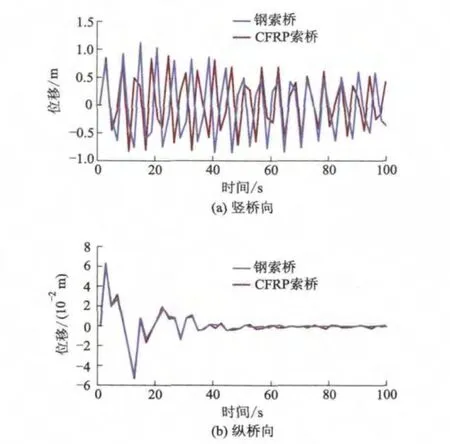
图7 主跨跨中位移时程

图8为CFRP索桥和钢索桥斜拉与悬吊交接区主梁弯矩时程曲线.由图8可知:CFRP索桥的弯矩响应值在每一时刻都小于钢索桥对应值，且CFRP索桥响应值的衰减速度快.

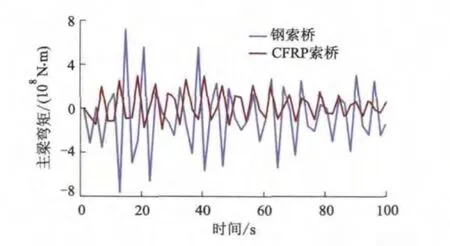
图8 主跨斜拉与悬吊交接处弯矩时程

2)主塔地震响应时程.图9为2种索斜拉-悬吊协作体系桥的主塔塔顶位移时程曲线.由图9可知:对于结构布置形式完全相同的两种索斜拉-悬吊协作体系桥，主塔顶部的位移响应差别不大，CFRP索桥塔顶位移响应时程变化趋势相对钢索桥有一定的滞后.由于本桥计算模型采用了全漂浮结构体系，地震波以纵桥向和竖桥向的形式输入.因此，桥塔顶端以纵桥向位移为主，竖桥向位移则很小.

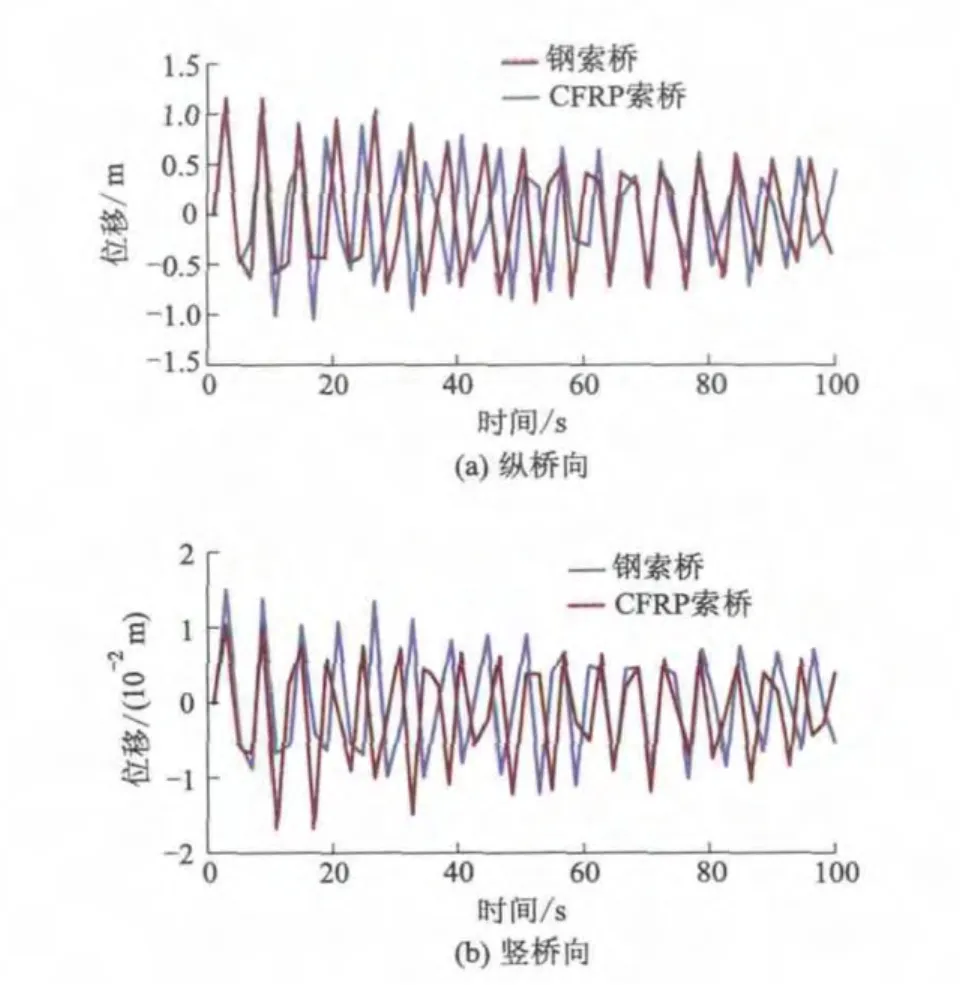
图9 塔顶位移时程

图10为CFRP索斜拉-悬吊协作体系桥和钢索斜拉-悬吊协作体系桥主塔塔底的内力时程曲线.由图10可知:CFRP索斜拉-悬吊协作体系桥和钢索斜拉-悬吊协作体系桥的塔底内力响应较为相似，CFRP索斜拉-悬吊协作体系桥塔底内力响应时程变化趋势相对钢索斜拉-悬吊协作体系桥有一定滞后.

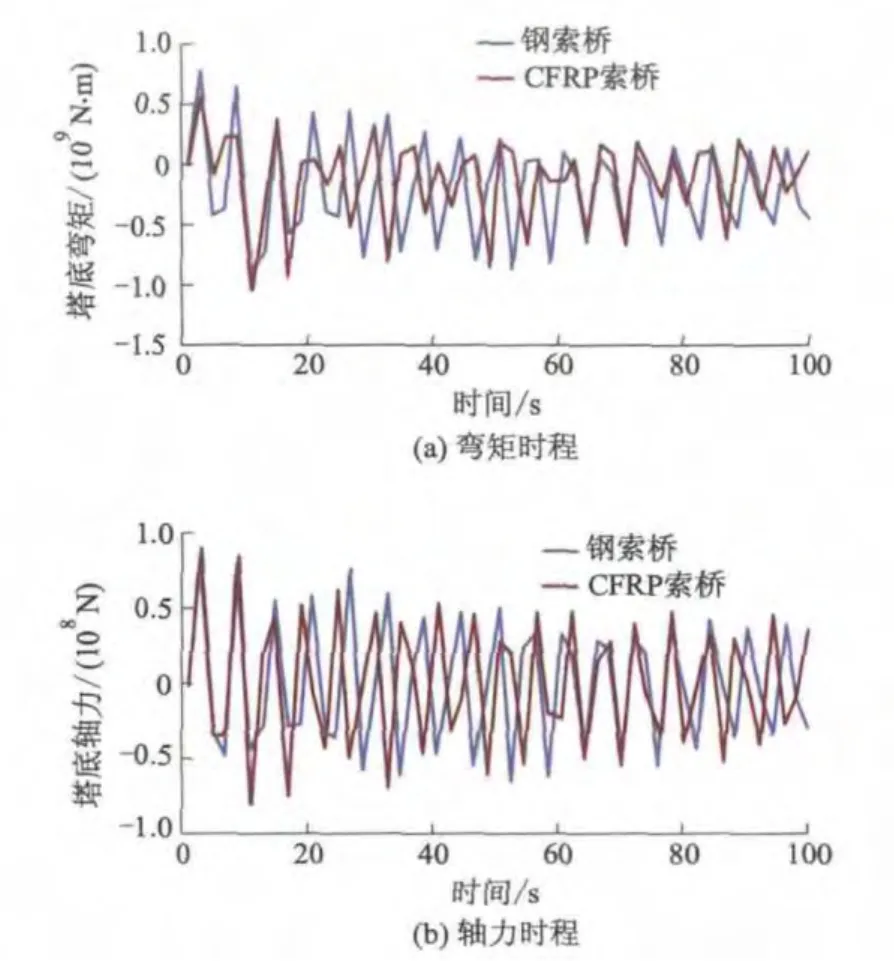
图10 主塔塔底内力时程

4.2.3 主要截面地震响应峰值比较分析

主要截面的位移及内力的地震响应峰值决定了桥体抗震设计，故应综合考虑静力和地震作用，以无载状态作为初始参考状态.表3为CFRP索桥和钢索桥主要截面的位移及内力地震响应峰值.

表3 主要截面的位移及内力响应峰值

由表3可知:CFRP索桥跨中的竖桥向位移峰值及塔顶的纵桥向位移峰值均低于钢索桥;跨中的纵桥向位移峰值及塔顶的竖桥向位移峰值都较小，且差距不大;对于相同结构布置形式的2种索桥，内力响应峰值的差异主要体现在主跨跨中斜拉与悬吊交接处截面的弯矩，CFRP索桥的弯矩峰值远小于钢索桥;主塔、边墩及辅助墩底部截面，CFRP索桥内力响应峰值较钢索桥略大，但差距并不明显.

5 结论

通过对主跨800 m的CFRP索斜拉-悬吊协作体系桥的动力特性及地震响应的三维有限元分析，得出以下结论:

1)此跨径下斜拉-悬吊协作体系桥表现出自振周期长、频率分布密集的特点;按照索的等轴向刚度原则将钢索替换为CFRP索时，整桥结构的前几阶振型基本一致，但CFRP索桥的各阶自振频率相应于钢索桥有一定的提高，有利于大跨度斜拉-悬吊协作体系桥结构抵抗低频激励.

2)相同地震波作用下，CFRP索桥的位移响应值与钢索桥接近，但内力响应值较钢索桥小，主要体现于主跨跨中截面的内力;在响应的衰减速度方面，CFRP索桥具有一定优势，说明采用CFRP索不会降低斜拉-悬索桥的抗震性能.

3)将CFRP索应用到大跨度甚至超大跨度斜拉-悬吊协作体系当中，能在一定程度上提高结构的抗震性能.

References)

［1］Meier U.Carbon fiber reinforced polymer cables:Why?Why Not?What If?［J］.Arabian Journal for Science and Engineering，2012，37(2):399-411.

［2］Grace N F，Navarre F C，Nacey R B，et al.Design-construction of Bridge Street Bridge—first CFRP bridge in the United States［J］.PCI Journal，2002，47(5):20-35.

［3］Lewis W J.A mathematical model for assessment of material requirements for cable supported bridges:implications for conceptual design ［J］.Engineering Structures，2012，42:266-277.

［4］Faggiano B，Martire G，Mazzolani F M.Cable supported immersed inversed bridge:a challenging proposal［J］.Procedia Engineering，2010，4:283-291.

［5］许 飞.CFRP索斜拉桥的静动力性能研究［D］.江苏大学理学院，2009.

［6］周士金，刘荣桂，蔡东升，等.CFRP索和钢索斜拉桥地震响应分析与抗震验算［J8］.建筑科学与工程学报，2009，26(3):76-81.Zhou Shijin，Liu Ronggui，Cai Dongsheng，et al.Seismic response analysis and seismic resistance checking of cable-stayed bridges with CFRP cables and steel cables［J］.Journal of Architecture and Civil Engineering，2009，26(3):76-81.(in Chinese)

［7］邓程远.CFRP索超大跨桥梁原型设计探索性研究［D］.江苏大学土木工程与力学学院，2011.

［8］刘荣桂，周士金，许 飞，等.CFRP索斜拉试验桥动态测试与地震响应分析［J］.长安大学学报:自然科学版，2009，29(6):47-53.Liu Ronggui，Zhou Shijin，Xu Fei，et al.Dynamic test and seismic response analysis of testing cable-stayed bridge with CFRP cables［J］.Journal of Chang'an University:Natural Science Edition，2009，29(6):47-53.(in Chinese)

［9］杜高明.大跨度自锚式斜拉-悬索协作体系桥结构性能分析［D］.大连理工大学桥梁工程研究所，2006.

［10］Soneji B B，Jangid R S.Influence of soil-structure interaction on the response of seismically isolated cablestayed bridge［J］.Soil Dynamics and Earthquake Engineering，2008，28(4):245-257.