PE模型SSFT解电波传播问题的虚部增量法

肖金光，周新力，刘晓娣

（1.海军航空工程学院 研究生管理大队，山东 烟台264001；2.海军航空工程学院 电子信息工程系，山东 烟台264001）

0 引 言

近年来，电磁环境问题越来越为军民用户所重视。采用数值法求解电波传播问题时，由Maxwell方程简化而来的椭圆型波动方程，一点的求解意味着必须同时求出计算域内全部点的解，实时求解较大计算域时计算量将极其庞大，抛物型方程 （parabolic equation，PE）忽略电波后向传播而只计算沿某坐标轴以较小角度形成的锥形区域内的前向传播。其解法有有限差分 （finite difference，FD）法、有限元 （finite element，FE）法和分步傅里叶 （split step Fourier transform，SSFT）法等。其中SSFT 能够方便的实现步进求解，步长选取灵活，适用于电波远距离传播计算［1］。基于PE 的SSFT 解法，美国研制了高级传播模型（advanced propagation model，APM），并以APM 为计算核心研制了 “高级折射效应预测系统” （advanced refractive effects prediction system，AREPS），用于美军的战场电磁态势评估［2，3］。国内众多研究所和院校等研究机构的专家学者对大气波导中PE计算模型关键技术、应用及实验验证进行了持续的跟踪研究［4－6］。

对于对流层电波传播的抛物方程求解，需要知道初始场、上下边界条件和大气折射情况。其中上边界需要满足第三类边界条件——Sommerfeld辐射条件，PE 的SSFT 解法需采取措施避免边界上的强反射影响到计算域。传统办法是在需要求解区域上加吸收层，层内采用窗函数进行滤波［2，6，7］，这种方法的优点是概念清楚，步骤清晰易理解，但在每一SSFT 步进上都要进行一次滤波。不难看出，窗函数滤波的功能和计算方法都具有单一性，因此本文提出一种等效方法——虚部增量法，将窗函数滤波的过程综合到环境折射效应计算中去，不再需要单独进行滤波计算。在理论推导的基础上，设计了实现步骤，分析了该方法的计算性能优势，并对2种方法的等效性做了仿真分析。

1 PE模型的SSFT解及吸收层窗函数法滤波

设电磁场时谐因子为e－iωt，忽略后向传播并作近轴条件下的窄角近似可得标准抛物方程 （standard parabolic equation，SPE）为

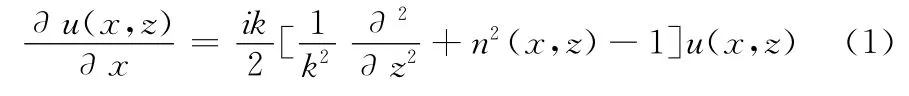
式中：u（x，z）——水平距离x、垂直高度z 处的场解，k——自由空间波数，n——大气折射率。

其适于求解远距电波传播问题的SSFT 解为［3］

式中：Δx——一次步进的水平距离变化，显然式 （2）是一种步进迭代算法。F、F－1分别表示傅里叶变换和傅里叶反变换，变换的点数 N 由 Nyquist 准则确定［4］，如式（3）所示

式中：zmax和pmax——输出高度和变换域最大值。

对于考虑地球曲率的修正折射指数M（x，z）有

将式 （4）代入式 （2）可得

式（5）中前后两指数项分别表征了传播媒质的折射效应和障碍物绕射效应，不妨分别称之为折射因子和绕射因子。这样只要知道初始场、上下边界条件就可以按照式（5）步进求解。初始场可以通过天线方向图的傅里叶逆变换求得。如果传播环境下边界是光滑平面，还可将FFT 进一步简化为正弦变换，若下边界为粗糙水面或陆地，可将下表面视为阻抗边界，采用DMFT 技术，但这2 种情况下，PE模型SSFT 解法的基本求解思路不变，在此不展开论述。

应用PE进行电波传播计算时，上边界必须满足Sommerfeld辐射条件，即场在无穷远处变为零，然而计算域不可能是无限大的，必须在需要求解区域的上方添加一个吸收层，层内电波完全被吸收，避免截断边界上的发生强反射造成需求解区域场值的 “污染”，造成计算误差［8］。常用吸收边界条件有基于媒质的和基于差分方程的两类，前者通过添加一个损耗媒质将向外传播的电波吸收［9］。PE 的SSFT 算法中只能使用损耗媒质法，在需求解区域上加吸收层，用窗函数对吸收层内的场进行滤波，保持场在需求解区域内保持不变，而在吸收层平滑衰减至0，即在最大高度处完全吸收。APM 中使用窗函数为 Cosine－tapered（Tukey）窗［2］

窗函数法相当于给折射指数添加了复数部分，使得吸收层中的传播媒介成为损耗媒介［8］。如果能够将窗函数的滤波作用等效成折射指数的一个增量，从而，将滤波的步骤综合到折射效应计算中去，可以减少计算步骤和计算量。下一节对这一思路进行理论推导。

立冬始降温，天冷好养肾。按照中医季节养生的理论，冬季对应五脏中的肾。立冬时心肺气弱，肾气强盛，饮食宜减辛苦，以养肾气。在饮食上依然要遵循“秋冬养阴”的原则，也就是说，少食生冷之物，但也不宜进食燥热之物，有的放矢地食用一些滋阴潜阳、热量较高的膳食为宜，同时也要多吃新鲜蔬菜以避免维生素的缺乏。

2 虚部增量法的理论推导

不妨设初始场和第n步的解分别为u0（x，z）和un（x，z）。滤波过程可以并入到式 （6）中

相当于在每次步进之前，先进行滤波。因为窗函数的滤波区域实质上只作用于吸收层，离散计算时，只对吸收层计算，而该部分并不作为计算结果输出，因此滤波运算完全可以前移到上一次步进结束而不会对输出计算结果造成任何影响，即

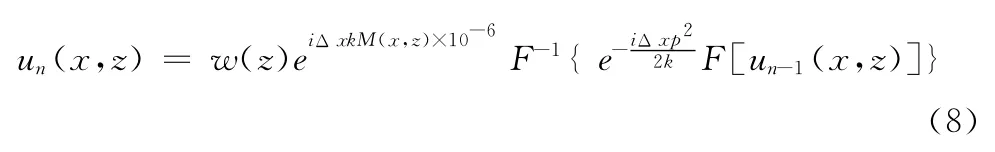
如果折射率剖面在水平上是不变的，即折射率n不随水平距离x变化，那么只需要将窗函数w（z）和折射因子整合为一个因子即可，每当折射率剖面变化 （多折射率剖面）时，需要重新计算该因子。对于多折射率剖面的情况，APM 使用线性插值法求解各个步骤上的折射率剖面，则在每一步骤上该因子都需要重新计算，即滤波过程每次都需要执行N／4 次乘法，对应于M 步PE，就要执行NM／4乘法。

不妨令

则

这样，由w（z）可求得ΔM ，必须要指出的是，ΔM 是虚数，而M（x，z）是实数，但由于式 （8）环境因子指数部分最终结果是复数，因此在计算上从实数到复数的转变没有影响，令

这一变化相当于给修正折射指数一个小虚部增量，相当于添加了损耗媒质，使得电磁波在该吸收层中完全被吸收，故将这种处理方法称为修正折射率虚部增量法，简称虚部增量法。

3 虚部增量法的算法流程设计及计算量分析

总结虚部增量法的实现步骤为：

步骤1 抛物方程模型及参数初始化，设定初始场、傅里叶变换的点数和下边界条件；

步骤2 根据窗函数求得虚部增量；

步骤3 根据当前步进上的大气修正折射指数及步骤2所得的虚部增量，求得等效大气修正折射指数；

步骤4 抛物方程步进求解和最高点场值置零；

步骤5 重复步骤3、步骤4，直至达到计算域距离终点。

基于虚部增量法的PE计算流程如图1所示。

通过将窗函数等价为折射率指数的虚部增量，一次滤波过程只需要N／4次加法即可实现，对应于M 步PE，需执行NM／4次加法运算。将NM／4复数乘法用加法运算即可实现，这一优化在进行电波传播实时求解，追求运算速度时计算量的节约达到的效果非常明显。对于插值获得大量折射率剖面，如每一步进上的折射率剖面，则有M 个修正折射指数剖面，使用窗函数滤波法和虚部增量法的运算量 分 别 为NM2／4 次复数乘法和NM2／4 复数加法，2 种方法所需运算量的差别是可观的，特别是长距离电波传播时PE步数较多情况，对降低PE 模型进行电波传播求解的计算量很有意义。

图1 基于虚部增量法的PE计算流程

4 仿真分析

假设辐射源工作频率为10GHz，天线类型为高斯型，归一化辐射强度，天线仰角为0，天线高度10 m，输出高度为100m，则由PE模型的参数设置原则，在需要求解区域上方添加高度为100／3 m 的吸收层，根据式 （3），垂直剖面上需要1024点FFT 运算。滤波窗函数为式 （4）所示Tukey窗，不妨设海面蒸发波导高度为14m，风速为5m／s，采用米勒布朗模型求解粗糙海面上的边界阻抗，用DMFT 法求解PE模型［10］。由所述虚部增量法，可得修正折射率的虚部增量。修正折射率剖面M（x，z）是实数，添加虚部增量后为M′（x，z）成为复数。实质上，蒸发波导折射率剖面M（x，z）就是M′（x，z）的实部，因而，只绘出了M′（x，z），如图2所示。

图2 虚部增量修正折射率

采用窗函数法和虚部增量法两种方法分别对折射因子进行处理，并与滤波前的复折射因子做比较如图3、图4所示。

图3 复折射因子的实部

图4 复折射因子的虚部

图3、图4表明，滤波前、窗函数滤波和虚部增量法3种情况下的复折射因子，在需要求解区域内复折射因子是完全重合的，在需要求解区域上部添加的吸收层内，窗函数法和虚部增量法2种方法所得得到的复折射因子完全一致，均平滑衰减为0。

为了验证应用虚部增量法进行PE模型的步进求解的效果，取10km 处场的垂直剖面如图5所示。

图5 传播距离10km 处的场强幅度

如图5 所示，在垂直方向上，垂直高度3／4 以上（对应于1024点FFT，就是768～1024 点区域）的吸收层内，电波波振面上场强幅度平滑衰减的趋势明显，并最终衰减为0，这是采用虚部增量法后，负折射因子在吸收层内平滑衰减对电波的作用结果。必须要说明的是此处所谓 “平滑衰减”是指电波在原有信号幅度基础上的平滑衰减，是信号包络的平滑衰减。这表明虚部增量法可使场在吸收层内平滑的衰减为0，从而满足了Sommerfeld辐射条件。

因此，仿真表明虚部增量法能达到与窗函数法相同的吸收效果，并降低了计算量需求。

5 结束语

针对抛物方程模型的分步傅里叶变换法求解电波传播时，上边界吸收层窗函数滤波法在每一步进上都需要进行一次滤波的问题，提出了与窗函数法等效的修正折射率虚部增量法，理论推导了这两种方法的等价关系，设计了计算流程，并对2种方法的等效性进行了仿真分析。通过将窗函数滤波等价为修正折射率的虚部增量，修正折射率虚部增量法节约了计算量，在多折射率剖面插值和长距离电波传播计算的情况下，较有意义。虽然本文的方法是基于Cosine－tapered窗函数推导的，但同样适用于其它类型窗函数情况。后续研究可以寻找更为高效的满足边界条件的窗函数，并利用本文的等价关系，得到等价的折射指数虚部增量，应用于PE的步进求解。

［1］WANG Hongguang，ZHANG Rui，KANG Shifeng，et al.Overview on parabolic equation model research for atmospheric ducting propagation ［J］.Equipment Environmental Engineering，2008，5 （1）：11－15 （in Chinese）.［王红光，张蕊，康士峰，等.大气波导传播的抛物方程模型研究综述 ［J］.装备环境工程，2008，5 （1）：11－15.］

［2］Sprague R A，Patterson W L，Barrios A E.Advanced propagation model（APM）version 2.1.04computer software configuration item（CSCI）documents［R］.Space and Naval Warfare Systems Command San Diego CA，2007.

［3］Sirkova I.Brief review on PE method application to propagation channel modeling in sea environment ［J］.Central European Journal of Engineering，2012，2 （1）：19－38.

［4］YAO Jingshun，YANG Shixing.A terrain parabolic equation model for propagation over the ocean ［J］.Chinese Journal of Radio Science，2009，24 （3）：493－497 （in Chinese）. ［姚景顺，杨世兴.抛物方程模型在海上电波传播中的应用 ［J］.电波科学学报，2009，24 （3）：493－497.］

［5］LIU Aiguo，CHA Hao.Experiment study of electromagnetic wave propagation loss in oceanic evaporation duct［J］.Chinese Journal of Radio Science，2008，23 （6）：1119－1203 （in Chinese）.［刘爱国，察豪.海上蒸发波导条件下电磁波传播损耗实验研究 ［J］.电波科学学报，2008，23 （6）：1119－1203.］

［6］YANG Chao.Critical technologies of wave propagation in atmospheric duct and its inversion ［D］.Xi’an：Xidian University，2010 （in Chinese）. ［杨超.大气波导中电磁波传播及反演关键技术 ［D］.西安：西安电子科技大学，2010.］

［7］LI Dexin，YANG Rijie，GUAN Wei，et al.Research on two－way parabolic equation modeling under irregular terrain environment［J］.Journal of Astronautics，2012，33（2）：235－240（in Chinese）.［李德鑫，杨日杰，管巍，等.不规则地形条件下的双向抛物方程模型研究［J］.宇航学报，2012，33（2）：235－240.］

［8］Apaydin G，Sevgi L.Numerical investigations of and path loss predictions for surface wave propagation over sea paths including hilly island transitions［J］.IEEE Trans on Antenna and Propagation，2010，58 （4）：1302－1314.

［9］Anwar Z.Efficient absorbing boundary conditions for modeling wave propagation ［D］.North Carolina State University，2005：1－3.

［10］Dockery GD，Awadallah RS，Freund DE，et al.An overview of recent advances for the TEMPER radar propagation model［C］／／Proceedings of IEEE Radar Conference，2007：896－905.