图论在物流运输中的实例研究
邱梦楠 朱梦茹 李 进
(泰州职业技术学院,江苏 泰州225300)
图论起源于18 世纪的哥尼斯堡七桥问题,发展于四色问题,用点和边来描述事物和事物之间的关系,是对实际问题的一种抽象,能够把纷杂的信息变得有序、直观、清晰。近30 年,由于与计算机技术的结合,成为数学中发展十分迅速新兴分支,现已广泛应用于工农业生产、交通运输、通讯、电力、经济管理、工程技术、生理学、控制论等领域,因此,图论越来越受技术与管理人员的重视。
物流学作为当今颇具影响力的学科,它以物的动态转化过程为主要研究对象,揭示了物流活动的内在联系,使物流系统在经济活动中从潜隐状态显现出来。 物流网络由线路和结点两个重要部分构成,基本的网络优化问题有:最短路径问题、最小生成树问题、最大流问题和最小费用问题等。 物流运输作为重要的物流网络优化问题,其方案的设计真接影响企业的运输成本和运输时间等。
本文运用图论理论,从图与网络的角度,以江苏省泰州市海陵城区主干线为例,构建图论模型,利用Floyd 算法,给出城区主干线上的结点间最短路径,并通过构建欧拉回路,给出最优巡回运输路径。
1 建立图论模型
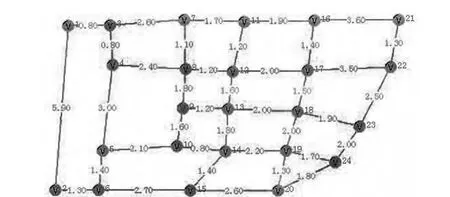
图1
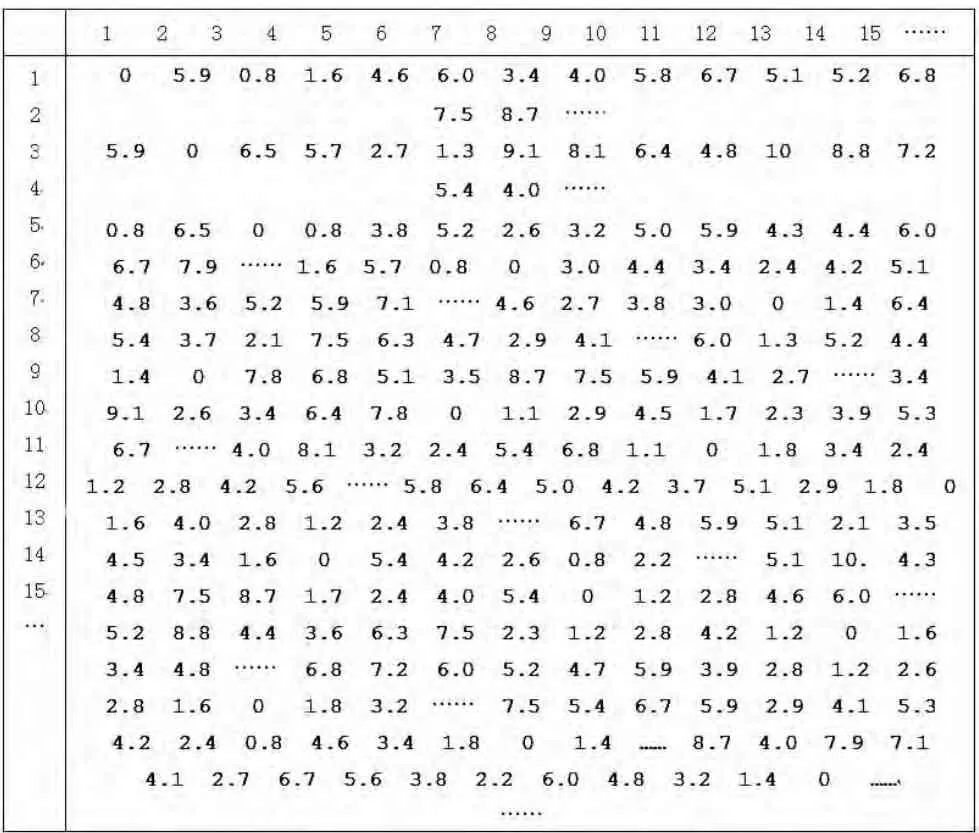
表1
设赋权连通无向图G(V,E)是城市道路构成的网络图,其中,V 表示图中所有的顶点集(vi),E 表示由城市道路构成的弧集,道路的长度用边权d(vivj)表示,如图1 所示。
2 结点间的最短路径
该图论模型,共有24 个结点,38 条路径。
由Folyd 算法求出结点间的最短路径,如表1 所示(单位:km)。
3 最优巡回运输路线
图G 中有14 个奇点,以它们为顶点集,作一完备图,边上的权为两端点在原图G 中的最短距离,将此完备加权图记为G1。
用Edmonds 算法求出G1 的最小权理想匹配,得到奇次顶点的最佳匹配:
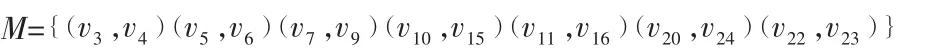
在G 中沿配对顶点之间的最短路径添加重复边,得欧拉图G2,如图2 所示。
再由Fleury 算法求出G2 中的欧拉巡回,即G2 中的一条欧拉巡回就是G 的一条最佳巡回运输路线,权值为87.1km。
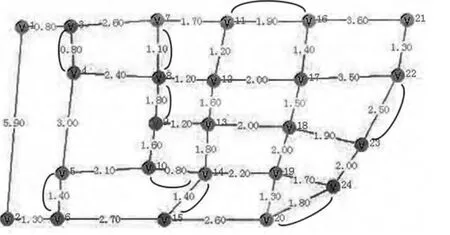
图2
[1]辛宇.基于运筹学图论的物流网络优化研究[J].中国外资,2011,06:125+127.
[2]王锐,甘凯.图论优化法在物流运输中的运用[J].商场现代化,2005,28:137-138.
[3]郭培俊,毛海舟.高职数学建模[M].浙江:浙江大学出版社,2010,12.

