高性能单频信号载波频偏估计算法

黄 超，索继东，于 亮

（1.大连海事大学 信息科学技术学院，辽宁 大连116026；2.大连理工大学 城市学院，辽宁 大连116600；3.大连理工大学 软件学院，辽宁 大连116600）

0 引 言

频率估计是从混有噪声的信号中估计一个或多个频率的技术。目前，国内外众多学者对此做了大量研究。如文献 ［1］给出了一种快速的频率盲估计算法；文献 ［2］给出了基于牛顿迭代的正弦频率估计方法；文献 ［3，4］从估计精度、估计范围及算法计算量等方面给出了一种基于自相关函数相位的频率估计算法；文献 ［5］提出了一种相关与旋转去调制的新算法，其对频偏变化的承受能力随着信噪比的增大而增强；文献 ［6］通过相位补偿去除BPSK调制引起的相位跳变，提高频偏估计精度；文献 ［7］在分析自相关函数特性的基础上，通过构造迭代函数及频率搜索的方法进行频率估计；文献 ［8］提出了一种在低信噪比下的频偏估计方法，但是复杂度过高；文献 ［9，10］提出了一种低复杂度的频偏估计算法，但在中低信噪比时性能与克拉美罗界有一定的差距；文献 ［11］分析了基于自相关函数相位频率估计方法的性能。文献 ［12］从FFT 域研究了一种快速高精度正弦波信号频率估计的递推算法。

提高频偏估计精度一般可从两方面来考虑：一是提高信号的发射功率，二是降低噪声功率。针对频偏估计精度、估计范围以及复杂度等方面的问题，本文在前人研究的基础上，提出了一种基于数据辅助的高性能载波频偏估计算法。充分利用序列扩频码的正交性，通过对引导码进行m序列扩频解扩，来降低噪声功率，从而提高估计频差信号的信噪比 （SNR）增益，然后基于最大似然法，通过采用一种新的迭代方法，快速准确地获取频偏估计值；且m 序列周期长度越大，性噪比增益也越大，估计性能也越好。

1 基于自相关函数的频偏估计算法

设发端机k时刻发送的符合为dk（引导码），其值为1或0，且1和0出现的个数相等；假设用于载波同步的信号已经获得符合定时且无符号间干扰。则在收端机得到欲处理的信号表示式为

γk与ηk 具有等效的相位噪声。由于引导码已知，为了消除数据信息的影响，对rk进行rk＊处理，其中为dk的共轭，且＝1，于是可得一新的序列

文献 ［3］利用相位展开的方法得出相关函数与频率估计的关系式

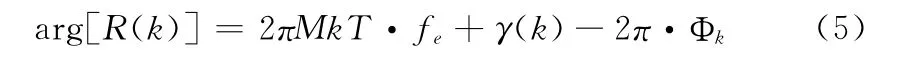
式中：Φk——使2πMkT·fe＋γ（k）－2π·Φk的值在±π之间的整数。于是得出频率估计式为

为了解决上式相位模糊的问题，文献 ［3］利用迭代方法得出新的频率估计式

通过计算机仿真结果表明，虽然文献 ［3］较好地解决了估计精度与估计范围的矛盾问题，且算法复杂度较低，但在信噪比较低时，估计性能不够理想。

文献 ［5］提出了一种新的相关与旋转去调制频率估计算法

其中，1≤k≤N－1。仿真结果表明，文献 ［4］在低信噪比时，具有较好的估计性能，但是随着N 的增大，计算量越来越大，不利于信号的实时处理。

部分汉日语IT新词在表记方式上都出现了缩略化的特征，这也是上述构词经济、效率原则的体现，即“用最经济的手段达到交际的目的”。

式中，通过固定的搜索步长估计载波频率。计算机仿真结果显示，在低信噪比时估计性能优于文献 ［1］算法，在高信噪比时，与文献［1］估计性能相当。

2 本文提出的算法

本文提出的载波频偏估计算法模型如图1所示，收端得到欲处理信号的表示式为

图1 载波频偏估计算法模型

图2给出feT ＝0，N ＝128，SNR ＝0dB 时，按照式（12）进行频差估计的仿真结果。可以看出，k 的取值在N／2附近时估计方差最小，估计精度最高。并且P值越大，估计精度也越高。

当信噪比SNR＞＞1时，噪声项uk可忽略，可得频差估计式为

图2 利用R （k）估计的方差特性

R（k）的计算相对复杂，它是衡量此类算法复杂度的重要因素之一。为了减小计算量，本文令ki＝4i，i＝0、1、…、ε，其中ε为使kε距离N／2最近的值。于是式 （16）可写为

由图2可知，R（ε）的估计性能最佳；能否准确地找出dε，直接影响的估计精度。本文采用的频偏估计迭代方法如下所示

式中：i≥2，0≤a≤3，a的取值也很关键，直接影响本算法的频差估计性能。下面通过仿真，给出a 的不同取值对估计性能的影响。仿真中，令feT ＝0.1，N ＝128，SNR＝0dB，P＝15；随着a的不同取值，其估计方差性能如图3所示。

图3 a不同取值下的性能比较

可以看出a ＝2，式 （18）具有最好的估计性能。此时，式 （18）可写为

频偏估计步骤如下：

（2）当i＝1，即ki＝4，令＝，由式 （17），可以找出d4；

（3）当i≥2，即ki≥16时，由式 （19）确定，且为取整函数；

（4）通过ε＋1次迭代，最终能找出正确的dε值；此时，用式 （17）进行频偏估计。

通过以上分析，本文提出的算法计算量较小；若N＝128，则ε＝3，即经过4次迭代就可完成频偏提取。

3 仿真分析

令观测的引导码序列长度N＝128，将文献 ［3，4，7］算法分别命名为算法A、算法B、算法C。

图4给出了本文算法的方差特性，从图中可以看出，m序列的周期P＝31时，即使在负信噪比条件下，本文算法的估计方差也能达到10－10，其估计性能优越。图5给出了本文算法与算法C 在均值特性方面的比较，可以看出，在信噪比相同条件下，本文算法的频差估计范围要宽于算法C。图6给出了在频差feT ＝0.1，算法A、B、C 及本文算法的R（k）迭代次数分别为8、64、32、4时，4种算法的性能随信噪比变化的曲线；可以看出，本算法的估计性能强于其它算法，算法复杂度低于其它算法；且估计性能随着m 序列的周期P增大而增强。

图4 本文算法估计的方差特性

4 结束语

提高频偏估计精度一般可以从两方面来考虑：一是提高信号的发射功率，二是降低噪声功率；这2种方法都可以提高信号的信噪比增益。在实际应用中，增大信号的发射功率是不可取的，为此，本文从降低噪声功率的角度，首先利用m 序列对引导码进行扩频解扩，降低信号的噪声功率，提高频偏估计信号的信噪比增益，然后基于最大似然法，通过采用一种新的迭代方法，能快速准确地获取频偏估计值。计算机仿真结果表明，本文算法的估计方差小、估计精度高、估计范围宽、复杂度低，具有很好的实用前景。

图5 本算法与算法C的均值特性比较

图6 各算法估计方差在不同性噪比下的性能比较

由于m 序列周期增大，会使基带信号的带宽增大，本文算法是通过牺牲信号的带宽来换取频偏估计精度的提高。在实际应用中，要综合考虑估计精度与信号传输带宽之间的矛盾问题。

［1］ZHANG Luping，WANG Jianxin.A fast blind carrier frequency estimation algorithm for digitally modulated signals ［C］／／6th International Conference on Wireless Communications Networking and Mobile Computing.IEEE，2010：1－3.

［2］DENG Zhenmiao，LIU Yu.The starting point problem of sinusoid frequency estimation based on Newton’s method ［J］.Acta Electronica Sinica，2007，35 （1）：104－107 （in Chinese）.［邓振淼，刘渝.正弦波频率估计的牛顿迭代方法初始值研究 ［J］.电子学报，2007，35 （1）：104－107.］

［3］HUANG Chao.A non－data－aided carrier frequency offset estimator for MPSK signal ［J］.Microcomputer Information，2009，25 （7）：87－88 （in Chinese）.［黄超.一种非数据辅助的MPSK 载波频偏估计算法 ［J］.微计算机信息，2009，25（7）：87－88.］

［4］LIU Shigang，GE Lindong.Feedforward carrier frequency offset estimator with wide range and high accuracy ［J］.Journal of System Simulation，2008，20 （18）：369－371 （in Chinese）.［刘世刚，葛临东.一种宽范围高精度前向载波频偏估计算法［J］.系统仿真学报，2008，20 （18）：369－371.］

［5］ZHANG Yi，OUYANG Zhixin，DENG Yunkai，et al.New high performance non－data－aided frequency estimation and implementation for QPSK ［J］.Journal of Xidian University，2013，40 （2）：226－234（in Chinese）.［张毅，欧阳志新，邓云凯，等.高性能无数据辅助QPSK频偏估计新算法与实现 ［J］.西安电子科技大学学报（自然科学版），2013，40 （2）：226－234.］

［6］LI Hong，QIN Yuliang，LI Yanpeng，et al.A phase compensation based algorithm for Doppler frequency rate estimation from BPSK coherent pulse train ［J］.Journal of Electronics and Information Technology，2010，32 （9）：2156－2160 （in Chinese）.［李宏，秦玉亮，李彦鹏，等.基于相位补偿的BPSK相参脉冲串信号多普勒频率变化率估计算法 ［J］.电子与信息学报，2010，32 （9）：2156－2160.］

［7］YIN Xiandong，WANG Jiafeng.A novel estimation of carrier frequency on the basis of autocorrelation ［J］.Journal of Southwest China Normal University，2012，37 （7）：51－56 （in Chinese）.［尹显东，王甲峰.一种新的自相关函数载波频率估计算法 ［J］.西南师范大学学报，2012，37 （7）：51－56.］

［8］CUI Yanpeng，HU Jianwei，YANG Shaoquan，et al.Novel frequency estimation of MPSK signals in low SNR environment［J］.Journal of Xidian University，2011，38 （5）：90－94 （in Chinese）.［崔艳鹏，胡建伟，杨绍全，等.一种低信噪比下MPSK 信号频率估计方法 ［J］.西安电子科技大学学报 （自然科学版），2011，38 （5）：90－94.］

［9］Giugno L，Luise M.Optimal pilot symbol distribution for efficient and low－complexity Doppler－shift and Doppler rate estimation in bursty transmission ［C］／／Proceedings of International Conference on Communication，2007：5993－5998.

［10］Cao Yan，Wei Gang，Chen Fangjiong.A Clo－sed－form expanded autocorrelation method for frequency estimation of a sinusoid ［J］.Signal Processing，2012，92 （4）：1852－1857.

［11］QI Guoqing，LV Jian.Variance analysis on sinusoid frequency estimators based on the argument of the sample autocorrelation function ［J］.Journal of Dalian Maritime University，2007，33 （4）：5－9 （in Chinese）. ［齐国清，吕健.基于自相关函数相位的频率估计方法方差分析 ［J］.大连海事大学学报，2007，33 （4）：5－9.］

［12］XU Jiajia，LIU Yu，DENG Zhenmiao，et al.A research of fast and accurate recursive algorithm for frequency estimation of sinusoid signal［J］.Journal of Electronics and Information Technology，2009，31 （4）：866－869 （in Chinese）. ［胥嘉佳，刘渝，邓振淼，等.正弦波信号频率估计快速高精度递推算法的研究［J］.电子与信息学报，2009，31 （4）：866－869.］