智能电网中基站的自适应电源管理方案

刘泽正，林亦雷，刘南杰，仲 浩，赵海涛

（1.南京邮电大学 通信与信息工程学院，江苏 南京210003；2.南京邮电大学 网络基因工程研究所，江苏 南京210003；3.国网上海市电力公司 信息通信公司，上海200122；4.江苏有线数据网络有限公司，江苏 南京210003）

0 引 言

为改善无线通信中的能耗问题，基于一种绿色通信系统模型［1］，通过可再生能源与智能电网［2］的有效结合来为无线基站提供能源，在考虑用户需求的前提下，最小化能量消耗所带来的花费。同时提出了一种基于基站供电环境历史数据的自适应电源管理方法［3］，该方案能够在存在许多不确定性 （如可再生能源的生产量、电价、无线传输的负载）的情况下有效控制无线基站的供电。

1 自适应电源管理系统模型的建立

自适应电源管理的模型如图1所示。系统模型的构成组件有：无线基站、电力网、可再生能源、电池、自适应电源管理控制器。

我们把可再生能源所能提供的最大的功率定为R kW；电池所能存储的最大电能为B°（kW／h），而电池单位时间流逝电量的速率为L，所带来的花费为Ploss。

自适应电源管理控制器有自己的机制，决定为电池和无线基站供电是通过可再生能源还是电力网。当无线基站需要供电时，自适应电源管理控制器将会以最小的能耗为目的进行决策的最优化。自适应电源管理控制器会定期的更新并保存以下的数据：电力网的电价、可再生能源的生产量、电池存量、无线基站的能耗。控制器要与电力网和可再生能源联网，这在智能电网中是可行的，如利用以太网或ADSL。自适应电源管理可以被看作是决策侧管理（demand side management，DSM）［4－6］。自适应电源管理控制器可以根据电力网给出的各种不同的电价以及可再生能源的生产能量来控制消费者的电量购买。当在高峰期时电价高，控制器将会推迟电量的购买，将电力消费的需求转移 （如转移给电池），直至非高峰期到来，如半夜。

无线基站的能耗分为2个部分，静态的和动态的。静态的能耗是一个固定的常数，无论基站是否与用户连接，只要基站处于活动状态就会消耗能量。另一方面，动态的能耗与基站的连接量和负载相关。在本专利中，我们考虑的是一种微型的无线基站，它的能耗主要依赖于负载的大小。基站的能耗可以表示为：C＝Est＋EdyN，Est，Est表示静态的能耗，Edy表示动态的能耗，N 表示连接量。

2 基于供电环境历史数据优化的自适应电源管理算法

无线基站的自适应电源管理最大的挑战就是环境和系统的不确定性。为了解决这一问题，随机最优化问题可以用公式表示出来并解决，使自适应电源管理控制器得出最好的决定，来使无线基站的能源的花费最小化。供电环境考虑的因素如下：

可再生能源：可再生能源如太阳能和风能的电量产生根据天气情况有很高的随机性。例如，太阳能要依靠阳光的量。多云和雨天是不可以测的，会减少能量的生产。

电力网的电价：由于电力网的许多不可预测情况 （如需求量），使得电价可能在某个范围内随机的分布。例如，在某一时期电价可能会变高，而通过电价信号特性，智能电网的用户会被告知电价。

无线基站通信负载：可达到的连接量是多变的，同样无线基站连接的需求也是依靠使用情况的 （如某一特殊情况而在成的高峰期）。这就造成了连接量N 是随机的。而且从上述能耗模型得到的能耗也是随机的。

2.1 基站供电环境历史数据统计

电价、可再生能源供电功率、无线基站能耗的统计方法如下：表1为算法中所用到的变量的总表。

表1 供电环境历史数据变量

考虑到一天24小时，且前后12 小时基站功耗，可再生能源供电功率差距可能过大，所以取决策期T＝24，即24小时优化一次，每个决策时段为1小时。我们定义总方案和分别为在t时期的电价、可再生能源产量、基站通信连接量的具体某一方案即子方案。总方案对应的概率为Pr（wk）。Pr（wk）即是指采用方案时，子方案为和，各个子方案采用自己对应的概率。Pt，Rt和Nt分别表示电力网电价的方案集合，可再生能源生产量的方案集合，无线基站的通信连接量方案集合。Ω＝ （Pt，Rt，Nt）是一个随机概率方案空间。如果有K 个方案，对应方案表示为w1，…，wK。当各个子方案的个数不同即出现和这种情况，取k1，k2和k3中的最大值 （如k3）为K，作为方案w 的个数，则pt和rt的方案数补到k3。多出来方案按概率为0计算。即＝，，）其中的和方案的概率为0。

我们把电价作为随机变量从一个离散的随机的集合中取值，如电价可以被定为 ｛0.74，0.74，1.23，0.74｝元每度电即，分别对应早上 （6：00－12：00），下午 （12：00－18：00），晚上（18：00－24：00），凌晨（0：00－6：00）。相应的也可以定为 ｛0.74，1.23，1.23，0.74｝即，考虑到下午如果是高峰期的话。像电价方案为｛0.74，0.74，1.23，0.74｝元每度电一样，可再生能源产电功率的方案可是设计为 ｛130，290，0，0｝瓦每小时，这些方案是从历史数据中得到的。

电价方案的统计方法：

对于方案中电价、可再生能源供电功率、无线基站能耗的概率分布是可以计算的。以60天为例，就电价而言，电价为 ｛0.74，0.74，1.23，0.74｝的天数为15 天，而｛0.74，1.23，1.23，0.74｝的天数为45天，这样就计算出第一种和第二种电价方案的概率分别为：15／60＝0.25；45／60＝0.75。

对于可再生能源供电功率我们也考虑2种方案，一种是晴天 （假设在7：00到18：00之间功率为196 Wh），一种是阴天 （假设7：00 到18：00 为100 Wh），以60 天为例，如果阴天天数为24天，晴天天数为36 天，则可再生能源供电功率为195 Wh的概率为0.6，功率为100 Wh的概率0.4。

无线基站能耗可以考虑为5种方案：一般高峰、一般中等、一般清闲、早上高峰、晚上高峰，且每分钟的连接到达率分别为0.56、0.22、0.15、0.8、0.8。因为24小时内，各方案有重复的，所以概率计算稍有不同。一小时为单位，根据连接到达率得到每小时基站的功耗。根据这个小时在60天里出现的天数计算其概率。比如早上8点，以上各方案的概率为0.1、0.1、0.2、0.4。

2.2 购电花费的随机规划建模

如用户在某一时段购买用电，所造成的花费我们表示为xtpt＋stLploss－。也就是购买电量的花费加上电池电量流失造成的花费减去退回电量的电价花费。

自适应电源管理控制器的多时段的随机规划模型用式（1）～式 （5）表示。，和就是环境历史数据统计出来的各概率方案。这个最优化的模型被分割成T 个决策时段，我们认为每个时段长度为1小时，K 为方案个数。

等式 （1）的目的是最小化各个时段的花费的期望，花费是由于买点和电池电量流失而造成的。是电价，pe是退回已购买的电量的电价，假设为固定值，且已经被WBS所知道。Ω是一个空间，Pr（wk）为空间内wk相对应的概率。方程中的基为从电力网中购买走的电量xt，w和电池的存储量st，w，是退回已经购买的电量。我们就是通过最优的方法求得这2个基站，以使花费最小化。电池的存量可以通过电力网或可再生能源提供。

等式 （2）是决策时段t时电量输入与输出的平衡式。t时段开始阶段电量的输入包括st，w，xt，w，可再生能源产生的电量rt，w。在决策时段t最后阶段，电量的输出包括电池剩余的存储电量st＋1，w，无线基站消耗电量ct，w且ct，w＝Est＋Edynt，w。等式的左边表示的是：t时段开始阶段购进的电量与电池存量和可再生能源产能的总和，也就是输入。等式的右边表示的是：电池在t时刻结束阶段 （t＋1时刻的开始阶段）的电量总和，也就是输出后的电量总和。

等式 （3）表示电池各时段的存储量要小于或等于电池的最大存储量B。

等式 （4）表示的是电池在初始时刻的存储量。

等式 （5）表示能量值功率值不能为负数。

2.3 随机规划模型求解

多时段的随机规划模型的求解，我们可以使用Benders分解法［7－9］。把优化问题分解为诸问题和多重子问题。

定义复杂变量就是一种阻碍问题得到简单直接的解且存在多重限制的变量。一旦复杂变量的值能够确定，那么最初的优化问题就可以分解成子问题。

提案：根据文献 ［3］可以看出，等式 （1）～等式（5）是一个由复杂变量的优化问题。如果复杂变量是xt，w和st，w，那么这个函数就可以分解为主问题和子问题，因为xt，w和st，w出现在式 （2）和式 （3）里。它们妨碍了问题的并行解。因此xt，w和st，w分别定为和。这样我们通过Benders分解法可以求出问题的解。Benders分解法师通过不停的迭代直到找到解为止。每一次迭代，主问题（式 （6）～式 （11））根据当时复杂变量的值求出解，并把解在子问题 （式 （12）～式 （15））中验算。目标函数的近似最优值的上下限可以计算出来。一旦解达到了充分优化，算法就停止。主变量 （式 （12）～式 （15））和对偶变量（）的近似最优质可以得出benders剪枝约束，可以提高求解速度和执行下一次迭代。

Benders分解法具体描述如下

步骤1 初始化：对于式 （6）～式 （11），v表示迭代次数，初始值为1。主问题的目标函数是从式 （1）中分离出来的。xt，w，v和st，w，v分别表示决策变量xt，w和st，w在第v次迭代时。αv表示子问题的额外能量花费 （）的近似值。αv将会在第v次迭代时计算出来。αlow表示的是下限，它可从历史数据中估计出来［3］。约束式 （9）表示的是在t时段w方案时，能量的输入要大于或等于能量的输出。步骤1只执行一次，步骤2到步骤4在算法中将会被多次执行。约束式（8）（叫做Benders剪枝约束）在步骤1时会忽略。这个约束会在下一次迭代时执行。为在第v次迭代时，对应于约束式（14）的对偶变量的值。该值将会在步骤4中被用到。

步骤2 求解子问题：子问题 （式 （12）～式 （15））可以求出解。约束式 （13）确保了在t时段方案w 时，能量的输入输出相等。和表示为主问题的固定的解。目标函数就是为了最优化额外电能花费。

步骤4 求解主问题：每次迭代过后v 都会加1。Benders剪枝约束将会被添加进主问题。换句话说，主问题构造中会有更多的约束，以使其更好的求解，因为这些约束都是基于子问题的近似最优情况的。主问题的最优解将会根据约束式 （8）来调节花费αv。Benders剪枝约束是根据迭代1 至v－1 中，子问题和主问题的近似最优解得到的。当主问题解决时，重复步骤2到步骤3。

2.4 自适应电源管理方案的流程

具体流程如下：

（1）数据收集。通过各种辅助工具收集电价、可再生能源产电量、电池存量、无线基站功耗的数据，发送给自适应电源管理控制器。

（2）设置方案。自适应电源管理控制器将收集到的数据更新并存储，并以固定天数 （如60天）为基础，通过历史数据，按照上文所提到的环境历史数据统计中的方法，设计出关于电价pt、可再生能源产电量rt、无线基站能耗nt的各种方案，并分别计算出其概率。得出随机概率方案概率空间Ω，然后根据pt，rt和nt组合成方案成K 个方案w和Pr（w）。

（3）自适应。每天结束时段根据式 （1）～式 （5）得出最优解问题，然后按照式 （6）～式 （15）进行Benders分解并进行迭代求解。第二天开始按照前一天所得结果控制相应的设备执行结果。然后返回第一步。

在以上的情况下，自适应电源管理控制器的作用就是在考虑无线基站能耗需求的情况下根据收集到的环境历史数据最小化买电所造成的经济花费。

自适应电源管理系统流程如图2所示。

3 实验结果与分析

3.1 参数设置

我们考虑可再生能源差量、电价、移动设备的数量是随机的，就电价而言我们考虑2种方案，如出现高峰用电的概率为0.6，出现非高峰用电的概率为0.4。各时段高峰期和非高峰期的平均电价分别为1.23 元和0.74 元每度。退回已购买电量的电价pe为固定的0.6元每度。我们考虑太阳能电池板来作为可再生能源。有10个太阳能板，每个太阳能板的供电容量为300 Wh。根据天气的统计，我们考虑两种方案，如晴天和阴天2种，每天6：00－18：00可再生能源的产量rt分别为1.95kWh和1.0kWh，且概率分别为0.6和0.4。电池的容量B为2kW。电池的初始容量B1假设为0.5kW。电池的电量流失速度L 为0.1%每小时。由于电量流失造成的花费ploss为0.06元每小时。我们考虑一种微型基站，这种基站与文献 ［10］相似。基站静态和动态的功耗参数 （Est和Edy）分别为0.19425和0.024kW每连接。无线基站能耗可以考虑为5 种方案：一般高峰、一般中等、一般清闲、早上高峰、晚上高峰，且每分钟的连接到达率分别为0.56、0.22、0.15、0.8、0.8。各方案的概率为0.1、0.1、0.2、0.4。

Benders分解法的宽容值ε为10－9。优化的执行期T 为24小时。

图2 自适应电源管理系统流程

3.2 实验仿真结果

图3显示了各时段不同的设备的平均功率。通过图3我们可以看出自适应电源管理算法主要是在考虑基站需求的前提下，依靠电池和可再生能源来最小化基站能耗带来的花费。我们发现电池通过可再生能源进行充电。基站每月的花费为75.60元。

我们考虑一种简单的自适应电源管理方案即不停的从电力购电来保证电池满量 （如1kW）。这种简单方案的每月花费大约为95.64元。显然自适应电源管理能减少花费，并且功耗低。虽然，每个基站每月节省仅仅20元，但是当基站数量较多时，节省花费的效果就明显了。同样，较少的从主电网购电，能减少CO2的排放。

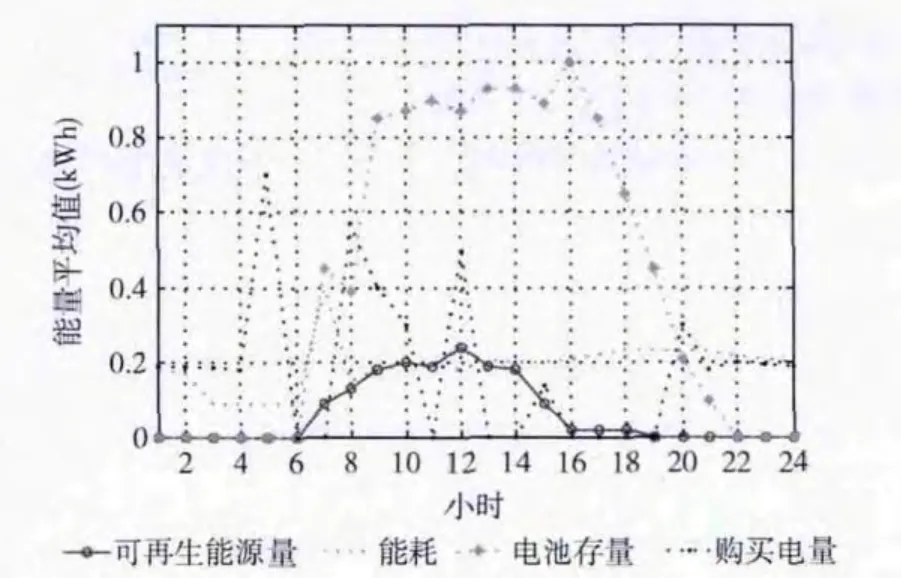
图3 可再生能源产量、基站能耗、电池存量、购买电量的平均值

图4显示了在不同的电池容量和可再生能源供电容量的情况下，每月花费的不同。随着电池容量的增加，当电价较低或可再生能源供电时，自适应电源控制器会储存更多的电量，这就能减少每月的花费。但是，一味的增加电池容量不能减少花费，因为电池的花费也增加了。此外，当可再生能源容量增加时，从主电网购买的电量会减少。但是，同样也不能忽视增加可再生能源容量而造成的花费。

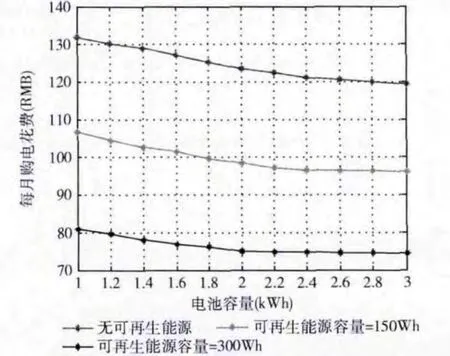
图4 不用电池存量下每月的花费

图5显示了在不同的连接到达率的情况下时，从主电网购电量和每月花费的不同。从图5可以看出有电源管理的情况下，从主电网购电的花费更低一点。这正体现了自适应电源管理有优化效果。

4 结束语

本文提出了智能电网中基于基站供电环境历史数据的自适应电源管理方案。利用可再生能源作为替代能源，不仅可以减少了能源的花费，而且可以减少CO2的排放。此外，自适应电源管理方案能根据供电情况管理基站的能耗。就这一点而言，优化问题被公式化，并可解除最优解。考虑到了可再生能源产量、电价、基站功耗的不确定性。实验结果表明，本文提出的自适应电源管理方案确实能够在考虑基站功耗的前提下，很好的适应供电环境，并根据供电化境的变化，而调整供电方案，减少了购电花费，和CO2的排放。

［1］Belfqih M，Gao J，Xu D，et al.Joint study on renewable energy application in base transceiver stations ［C］／／Incheon Proc Intl Telecommunications Energy Conf，2009：1－4.

［2］Bu S，Richard Yu F，Cai Y，et al.When the smart grid meets energy－efficent communications：green wireless cellular networks powered by the smart grid ［J］.IEEE Transactions on Wireless Communication，2012，11 （8）：3014－3024.

［3］Tang GQ.Smart grid management ＆visualization：Smart power management system ［C］／／Canada：Int Corp，Toronto，ON，2011：1－6.

［4］Chen Xiangting，Zhou Yuhui，Duan Wei，et al.Design of intelligent demand side management system respond to varieties of factors［C］／／Nanjing：Intl Conference on CICED，2010：1－5.

［5］Logenthiran T.Demand side management in smart grid using heuristic optimization ［J］.IEEE Transactions on Smart Grid，2012，3 （3）：1244－1252.

［6］Sui Huibin.A demand side management model based on advanced metering infrastructure ［C］／／4th Intl Conference on DRPT，2011：1586－1589.

［7］Conejo A J，Castillo E，Minguez R，et al.Decompo－sition in linear programming：complicating variables ［M］.Decomposition Techniques in Mathematical Programming，Springer，2006：107－139.

［8］Birge J R.Decomposition and partitioning methods for multistage stochastic linear programs［J］.Oper Res，1985，33 （1－3）：989－1007.

［9］Benders J F.Partitioning procedures for solving mixed－variables programming problems ［J］.J Numerische Mathematik，1962，4 （1）：238－252.

［10］Arnold O，Richter F，Fettweis G P，et al.Power consumption modeling of different base station types in heterogeneous cellular networks ［C］.Proc Future Network and Mobile Summit，2010：1－8.