位置扰动的粒子群算法

薛 敬，靳雁霞

（中北大学 电子与计算机科学技术学院，山西 太原030051）

0 引 言

粒子群优化算法［1］（particle swarm optimization，PSO）是人类受到自然界生物活动规律的启发而进一步研究发展起来的全局随机优化算法，它又被称为鸟群算法。PSO 算法自诞生以来，由于其具有的易于理解和操作、收敛速度较快、设置和调整的参数较少等优点，在短期内得到很大发展，目前该算法已经在数字图像处理［2，3］、神经网络训练［4］、无线通信技术［5］、虚拟碰撞检测［6］等多个领域得到了成功应用。然而，经过研究人们发现传统粒子群算法存在着粒子多样性差、全局搜索能力差等缺陷和不足。针对这些问题，研究人员提出了相应的改进算法。文献［7］通过改变位置更新公式，使得算法更有效率的达到收敛。文献［8］提供了新的学习策略，提高了算法全局搜索能力；文献［9］分析了粒子群搜索的随机行为，提出了更有稳定性和收敛性的算法。

本文从优化群体最优位置的角度出发，提出了对基本粒子群算法的改进算法。在粒子进化过程中，群体最优位置接受其它各粒子最优位置在某些维上已经搜索到的位置数据的扰动，从而达到了跳出局部最优和增强全局搜索能力的目的。

1 基本粒子群算法

基本粒子群算法采用的是群体和优化的概念［10］，这也和其它很多优化算法相类似。PSO 算法区别于其它优化算法的地方在于，它没有针对个体使用淘汰的进化算子，而是将所有个体都当作是在空间内飞行的鸟，它们不会被其它粒子替代，且以一定的速度在空间中飞行寻优。在算法中，设Xi＝（xi1，xi2，…xin）来表示粒子i的在当前搜索空间中的位置；Vi＝（vi1，vi2，…vin）来表示粒子i在当前搜索空间中的速度；Pi＝（pi1，pi2，…pin）来表示粒子i自身最优位置；Pg＝（pg1，pg2，…pgn）来表示群体经历最优位置或者粒子i邻域中的最优位置。

PSO 算法中各个粒子将按式（1）、式（2）改变速度和位置

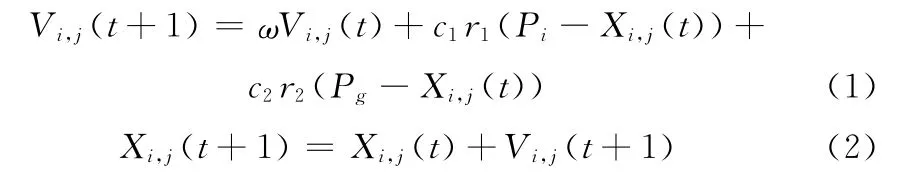
上述式（1）、式（2）中，c1为粒子向自身学习的权重系数，c2为粒子向群体经验学习的权重系数；r1、r2一般为介于（0，1）之间相互独立的正态随机数，它们的共同作用是动态随机调节粒子向自身学习和向群体学习的权重，保证了算法的随机性。通过设置各个粒子的速度范围区间［vmax，vmin］和位置范围区间［xmax，xmin］，便可以对粒子的搜索和移动加以适当的限制。

2 改进的位置扰动粒子群算法

2.1 PDPSO 算法基本思想

粒子群算法在N 维空间搜索时，每次迭代后都会产生粒子i 自身最优位置Pibest和群体经历的最优位置Pgbest，Pgbest并不代表在搜索空间的每一维上都在最优位置，相反，Pibest有时候可能会在某些维上比Pgbest更接近理论的最优位置。通过对粒子自身位置随机维的计算产生扰动，可以在这些维上对Pgbest有积极的影响，使得搜索跳出局部最优，同时提高了寻优的收敛精度。

2.2 基于加权计算的扰动

为了实现算法，一方面，抽出个体最优位置适应值仅次于P′gbest的M 个粒子作为扰动粒子，M 可根据粒子总数目和具体研究问题目标而定。记下它们的自身最优位置（gbest1，gbest2，……，gbestM）和所对应的适应值（fitgbest1，fitgbest2，……，fitgbestM）。随机选取R 个不同的维，处理具体问题时，可以通过搜索空间的维数N 来选择R 的大小。通过分别对这些扰动粒子R 个维上的加权计算，得到计算结果之后，以计算结果为均值，生成正态随机扰动对Pgbest的相应的R 个维上扰动。令生成的扰动值代替Pgbest对应维上的值，具体来说，如果第n维属于被选中的R 个维，那么对于第n 维而言，则有zbestn＝rn。若被扰动后P′gbest的适应值好于扰动前Pgbest的适应值，即f（P′gbest）优于f（Pgbest），则接受扰动进化，令Pgbest＝P′gbest，并重新记下f（P′gbest）作为全局最优值，反之，则拒绝扰动进化，保持原有数据。

其中，zbestn为粒子群体最优位置第n 维上的值，式（3）为第n维上扰动粒子的加权值μn 的计算公式，式（4）为第n维生成正态随机扰动rn的公式。R 是小于N 的正整数

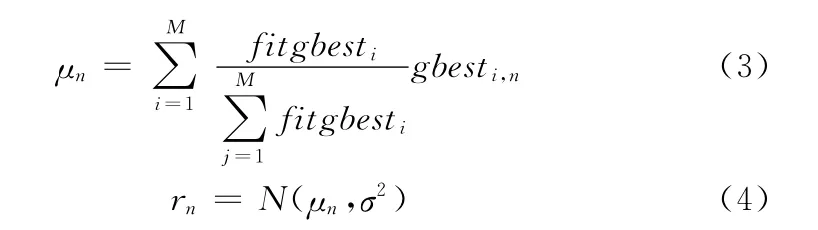
式（3）中，gbesti，n为第i 个粒子个体最优位置第n 维上的值。式（4）中，σ2为正态分布的方差，其取值规则满足式（5）

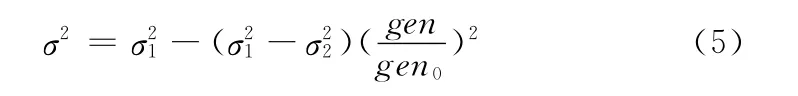
2.3 基于平均值计算的扰动

为了实现算法，另一方面，挑选出每一个粒子的自身最优位置中随机的Q 个维，分别求出Q 个维的算数平均值，处理具体问题时，可以根据具体搜索空间的维数大小来选择Q 值的大小。并通过这些算术平均值产生正态随机扰动值对Pgbest对应的Q 个维上进行扰动，即令生成的Q 个维上扰动值代替Pgbest对应维上的值，具体来说，如果第n维属于被选中的Q 个维，那么对第n维而言，则有zbestn＝rn。若被扰动后P′gbest的适应值好于扰动前Pgbest的适应值，即f（P′gbest）优于f（Pgbest），则接受扰动进化，令Pgbest＝P′gbest，并重新记下f（P′gbest）作为全局最优值，反之，则拒绝扰动进化，保持原有数据。

其中，式（6）为第n 维上算术平均值averagen计算公式，式（7）为第n维生成正态随机扰动rn的公式。Q 是小于N 的正整数

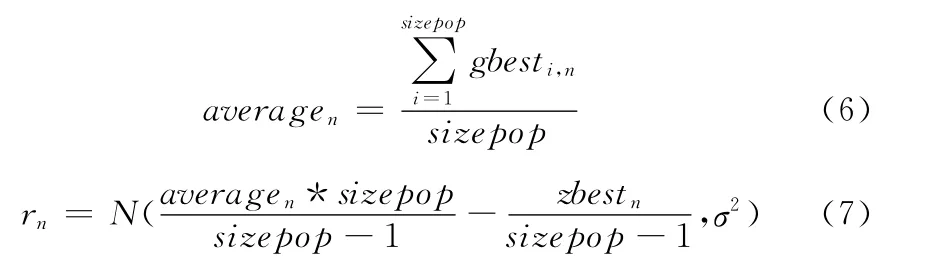
式（6）中，sizepop 为群体的总粒子数。在式（7）中，σ2为正态分布的方差，其取值规则满足式（5）。

2.4 算法实现步骤

步骤1 选定算法所必须的参数，随机初始化各粒子的位置和速度参数。

步骤2 根据约束函数算出粒子的具体适应值，并且记录每个粒子的个体最优位置和粒子群的群体最优位置。

步骤3 选出个体最优位置适应值仅次于Pgbest的M 个粒子作为扰动粒子，通过式（3）、式（4）、式（5）产生对Pgbest的R 个维上的扰动值，若扰动后P＇gbest的满足进化条件，则接受扰动进化，反之，则拒绝。

步骤4 随机选出个体最优位置的Q 个维，通过式（5）、式（6）、式（7）产生对Pgbest相应维上的扰动值，若扰动后P′gbest满足进化条件，则接受扰动进化，反之，则拒绝。

步骤5 根据式（1）、式（2）在每一代进化后更新粒子的速度与位置参数。

步骤6 判断寻优结果是否满足寻优停止条件，若不满足条件，则重新返回去执行步骤2；若满足，则接着执行步骤7。

步骤7 输出最终寻优结果。

3 算法仿真测试与实验

3.1 基本测试函数

测试实验选择了几个性质不同的基本测试函数对PSO和PDPSO 两个算法进行了测试仿真，主要目标是测试两个算法对单峰值函数和多峰值函数，尤其是多峰值函数搜索精度和全局寻优能力，并通过测试结果，对比两个算法对相同函数的全局寻优的精度和能力。

下面的F1、F2、F3、F4 是测试选择的4 个用于两个优化算法进行比较的基准函数。

Sphere函数，它在（x1，x2…xi）＝0时达到全局的最小值0。

Ackley函数，函数在搜索空间中存在着大量的局部极小值点，当（x1，x2…xi）＝0时达到全局的最小值0。

Rastrigrin函数，函数在搜索空间中有大量正弦凸起的局部极小值点，当（x1，x2…xi）＝0时达到全局的最小值0。

Levy函数，函数是一个有着很多个局部最小值的多峰值函数。当（x1，x2…xi）＝1时达到全局的最小值0。

3.2 测试参数

测试取最大迭代次数gen0＝2000，PSO 和PDPSO 算法中ω都取0.8，且c1＝c2＝2，粒子群规模sizepop＝30，搜索空间维数N＝10。PDPSO 算法中，扰动粒子数目M＝2，扰动维的数目R＝Q＝2，初始正态方差＝5，正态截止方差＝0.05。迭代结束条件是，当进化代数大于最大迭代次数时，停止迭代并输出最终结果。

3.3 测试仿真结果

在测试环节中，为了方便在不同算法之间的考察比较，测试用每一种算法在同一个测试函数上独立运行50次，记录并且计算出这50次测试搜索寻优结果中的最优值、平均值、最差值，以及每种算法在各测试函数中的稳定性，即算法满足在误差范围的精度以内的比例。

函数的最优位置、最优值和误差范围见表1。

表1 4个标准测试函数最优值及其误差范围

测试具体数据见表2。

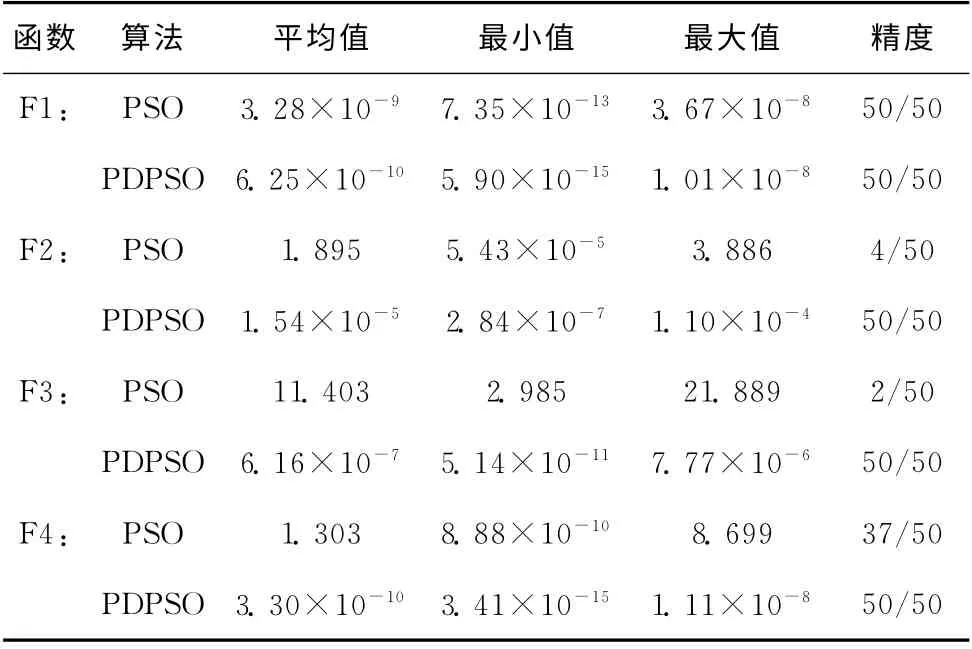
表2 4个标准测试函数的测试结果对比

由表2可得到结论：一方面，虽然PSO 和PDPSO 两种算法对于单峰值函数F1都具有很精确的收敛精度，但是PDPSO 算法却有略高的收敛精度和稳定性。另一方面，测试结果表明，对于多峰值函数F2、F3、F4，PSO 算法的搜索结果精度并不理想，而PDPSO 算法却有着比较相对很高的收敛精度和稳定性，也就是说，在处理多峰值优化问题时，PDPSO 算法有着明显优于PSO 算法的寻优精度和能力，针对于一些函数和问题，它能够让收敛精度提高成千上万倍。

为了进一步对比和说明PDPSO 算法良好的寻优能力，测试通过图片对比了PSO 和PDPSO 算法应用于同一约束函数的收敛曲线。如图1～图3所示，图中坐标轴橫半轴表示迭代次数，纵半轴表示适应值。

由图1～图3可以看出：在寻优过程中，当PSO 算法处理多峰值函数出现了停滞，陷入了局部最优值的时候，便已经很难从局部最优中跳出，结果只能收敛于局部极值点，这是由于其全局搜索能力不够造成的。而PDPSO 有着更强的跳出局部最优值的能力，它在进化过程中，能够让粒子进一步在解空间的其它区域中搜索寻优，使得进化继续进行下去，具有更强的全局搜索能力。

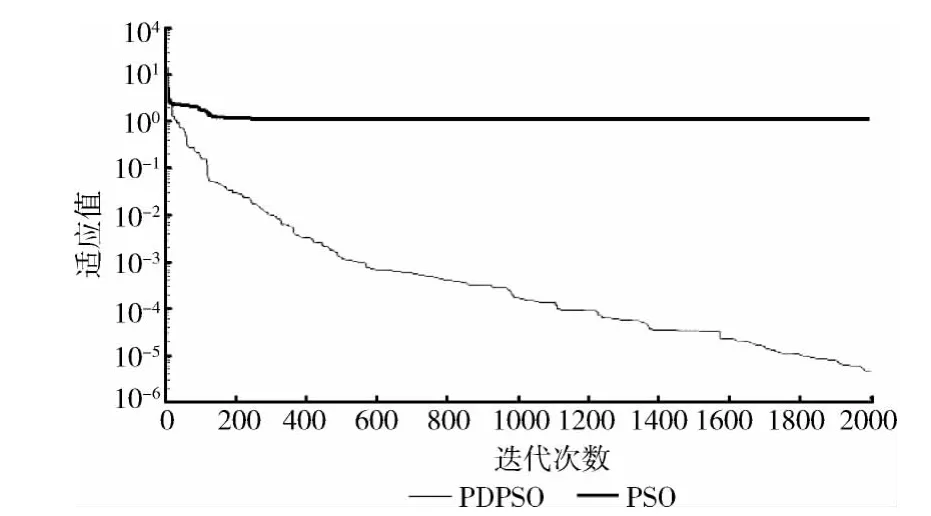
图1 十维Ackley函数对比

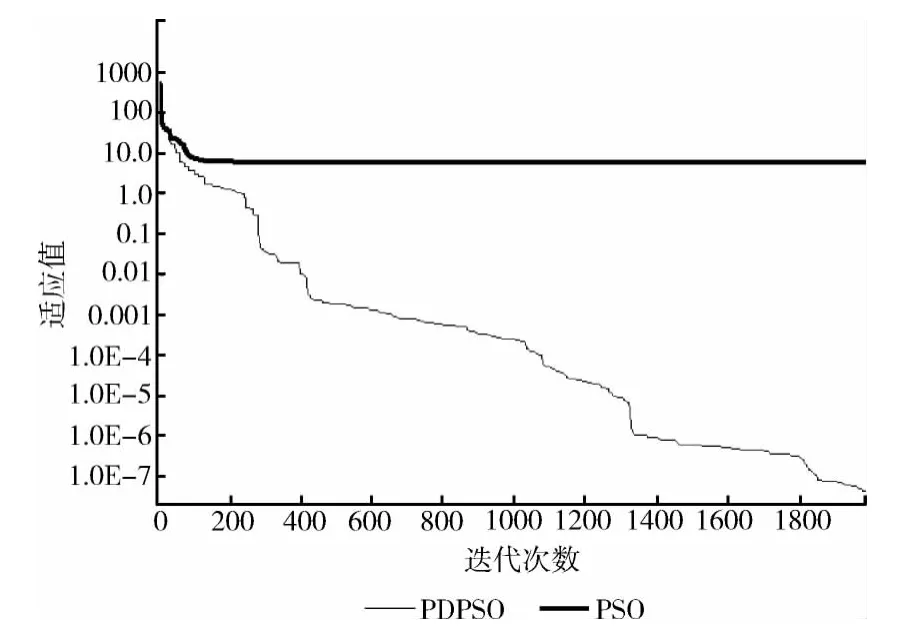
图2 十维Rastrigrin函数对比

图3 十维Levy函数对比

4 结束语

PDPSO 算法通过采用个体最优位置产生扰动值对全局最优位置扰动进化的思想方法，使得粒子群的粒子在每代更新时，全局最优位置也能有条件的向个体最优位置学习，充分发挥了粒子个体最优位置的更大效用，达到了全局最优位置和个体最优位置互相学习的效果。有了这样的改变，PDPSO 算法也克服了基本PSO 算法的全局搜索能力不强、容易陷入局部极值点而无法跳出、对于有些函数问题搜索精度不高等不足之处。最后，测试实验的事实证明：PDPSO 的确比基本PSO 具有更强的全局搜索寻优能力和收敛精度。

［1］JI Zhen，LIAO Huilian，WU Qinghua.The particle swarm optimization and application ［M］.Beijing：Science Press，2009：16－80 （in Chinese）.［纪震，廖惠连，吴青华.粒子群优化算法及应用 ［M］.北京：科学出版社，2009：16－80.］

［2］Muruganandham A，Wahida Banu Dr R S D.Adaptive fractal image compression using PSO ［J］.Procedia Computer Science，2010，2：338－344.

［3］WEI Ding.A new method for image noise removal using chaos－PSO and nonlinear ICA ［J］.Procedia Engineering，2011，24：111－115.

［4］YU Zhifu，LI Junwu，LIU Kai.Radar emitter recognition based on PSO－BP network ［J］.AASRI Procedia，2012 （1）：213－219.

［5］HU Yu，WANG Xiaohui.PSO－based energy－balanced double cluster－heads clustering routing for wireless sensor networks［J］.Procedia Engineering，2011，15：3073－3077.

［6］LI Wenhui，WANG Tianzhu，WANG Yi，et al.Stochastic collision detection between deformable models using particle swarm optimization algorithm ［J］.Journal of System Simulation，2006，18 （8）：2206－2209 （in Chinese）. ［李文辉，王天柱，王祎，等.基于粒子群面向可变形物体的随机碰撞检测算法 ［J］.系统仿真学报，2006，18 （8）：2206－2209.］

［7］ZHU Tong，LI Xiaofan，ZHU Mingwen.Improved particle swarln optimization algorithm with position weighted ［J］.Computer Engineering and Applications，2011，47 （5）：4－6（in Chinese）.［朱童，李小凡，朱明文.位置加权的改进粒子群算法 ［J］.计算机工程与应用，2011，47 （5）：4－6.］

［8］XIE Zhenggui，ZHONG Shaodan，WEI Yuke.Modified particle swarm optimization algorithm and its convergence analysis［J］.Computer Engineering and Applications，2011，47 （1）：46－49 （in Chinese）.［谢铮桂，钟少丹，韦玉科.改进的粒子群算法及收敛性分析 ［J］.计算机工程与应用，2011，47（1）：46－49.］

［9］WU Xiaojun，YANG Zhanzhong，ZHAO Ming.A uniform searching particle swarm optimization algorithm ［J］.Acta Electronica Sinica，2011，39 （6）：1261－1266 （in Chinese）.［吴晓军，杨战中，赵明.均匀搜索粒子群算法 ［J］.电子学报，2011，39 （6）：1261－1266.］

［10］ZENG Jianchao，JIE Jing，CUI Zhihua.Particle swarm optimization algorithm ［M］.Beijing：Science Press，2004 （in Chinese）.［曾建潮，介婧，崔志华.微粒群算法 ［M］.北京：科学出版社，2004.］