方差能量最小化活动轮廓模型超声图像分割

李海燕，邹天宁，李支尧，张榆锋，陈建华，施心陵

（1.云南大学 信息学院，云南 昆明650091；2.昆明医科大学 第三附属医院乳腺外科，云南 昆明650106；3.昆明医科大学 第三附属医院超声科，云南 昆明650106）

0 引 言

超声成像因实时、无创、低价及对人体危害小等特点被广泛用于临床医学诊断。然而，超声成像由于其固有的干涉现象导致图像含有大量的斑点噪声而且信噪比和对比度较低，给超声图像分割带来极大困难进而导致临床诊断的不精确或者错误。因此有效的自动分割技术对于超声图像的后期处理及诊断具有重要意义。

在众多的图像分割技术中，活动轮廓模型因其良好的分割性能而被广泛应用于医学图像分割。跟据图像特征和目标先验知识，现有的活动轮廓模型可分为基于边界的活动轮廓模型［1］和基于区域的活动模型［2，3］。基于边界的模型利用图像梯度信息控制轮廓曲线的演化停止在目标边界，这类算法对图像的噪声和弱边缘敏感，会导致过多的虚假边缘和边缘泄露，容易分割失败。基于区域的模型依靠全局信息引导轮廓的演化，一定程度上可以处理图像的灰度不均匀问题，但由于需要把水平集函数初始化或重新初始化为一个符号距离函数，使得计算成本相当高［4］。李［4，5］提出了局部像素信息最小化的活动轮廓模型，能有效地处理图像灰度不均匀问题，但易受斑点噪声的影响。文献［6］提出用局部强度的均值和方差描述局部的像素分布，可以有效地克服图像像素不均匀的问题和易受噪声影响的问题，但局部强度的均值和方差依赖于模型的先验知识。

针对上述活动轮廓模型存在的不足，提出了基于方差能量最小化的活动轮廓模型。该模型利用不同的高斯分布的均值和方差描述局部的强度。首先，利用内核函数定义待分割目标附近能量信息的高斯分布；然后，基于空间变量函数的局部均值和方差构建局部高斯分布能量并在全局图像域整合局部能量，得到局部高斯分布能量。最后，将残差能量最小化能量函数并入水平集的标准变量方程，在能量泛函极小化驱动水平集曲线演化到目标边界的过程中，利用局部像素信息求取高斯分布的均值和方差识别不同区域亮度的差异。提出算法的创新点在于：①提出算法定义了双积分，首先用水平集函数的内核函数定义该点附近的图像信息局部高斯分布。然后，在水平集的演化公式中，将局部能量再次积分为二重积分。②提出算法根据变微分原理推导目标区域亮度高斯能量方程的均值和方差，而不依赖先验知识。

1 高斯方差能量最小化的活动轮廓模型

设I：Ω→R 表示给定的图像区域，C 是封闭的零水平集函数（Φ＝0）的曲线。通过近似的Heaviside函数的平滑函数（Hi＝H（Φ），Ho＝1－H（Φ））把图像区域Ω分为Ωin和Ωout两部分。能量函数极小化时，目标边界曲线C 近似等于零水平集函数Φ。图像的强度P（I）用概率密度函数（pdf）的最大似然函数来表示。它的能量泛函数为

式 （1）中的第一个积分表示图像数据，第二个积分用以控制曲线平滑的演化。λ是权重系数，为正常数。以u 和σ为参数的概率密度P（I（x））定义为

假设估计值来自于图像域Ω的每个像素所围绕的中心局部区域，则相应于能量式（1）的内部区域方程为

其中

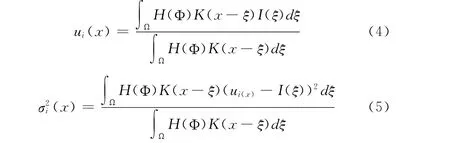
式中：K（·）是定义在位置x 空间局部性的内核函数，在本分割算法中，用标准偏差σK的高斯核函数表示，即

采用Gteaux导数计算水平集函数Φ：Ω →R 的梯度下降。对于任意的像素x，有

式中：ψ（x）可以是任意的测试函数。

由式 （7）可得下列方程

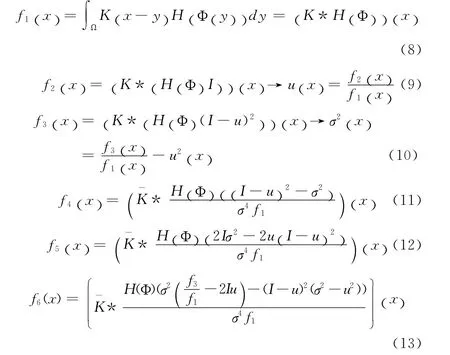
可以使用递归的高斯滤波实现式 （14），然后根据式（14）对能量Ω0即方程 （1）的第二项的欧拉－拉格朗日方程进行推导，为了使式 （1）能量最小，对水平集函数Φ使用标准梯度下降法，即

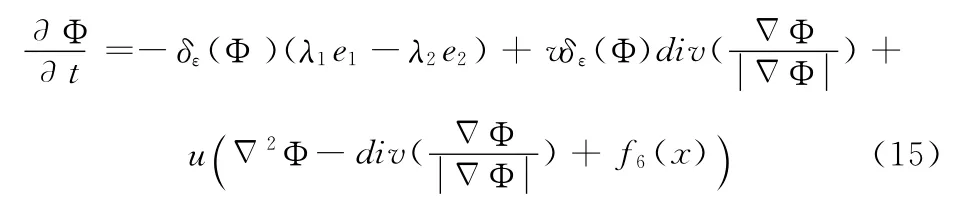
式 （15）的推导过程可参见文献 ［5］，它的稳态解的零水平集，即为所求的目标曲线C。其中δε为Heaviside函数的平滑狄拉克函数［7］，e1和e2的方程为

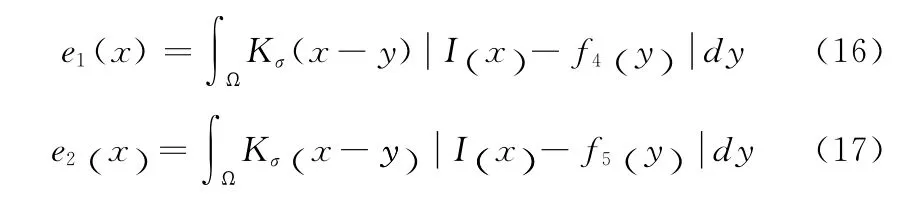
2 算法实现

（1）通过零水平集Φ0初始化水平集函数Φ；

（2）用式（4）和式（5）计算目标区域的均值ui（）x 和方差（）x ；

（3）用式（15）的偏微分方程，求解水平集函数Φn到；

（4）检查收敛函数Φ，确定结果是否达到稳定状态，否则返回（2）继续循环计算。

其迭代结果的零水平集曲线就是所求的目标边界曲线C。

（5）根据结果图与原图像的相对位置关系，得到的目标边界，叠加到原图像上。

其中，Φ0为初始条件。为了让提出的方法可以更好的应用于超声图像且对初始位置不敏感，我们将初始条件设置为

式中：C0——事先定义好的常数，而Ω0为初始边界曲线，将其设置为

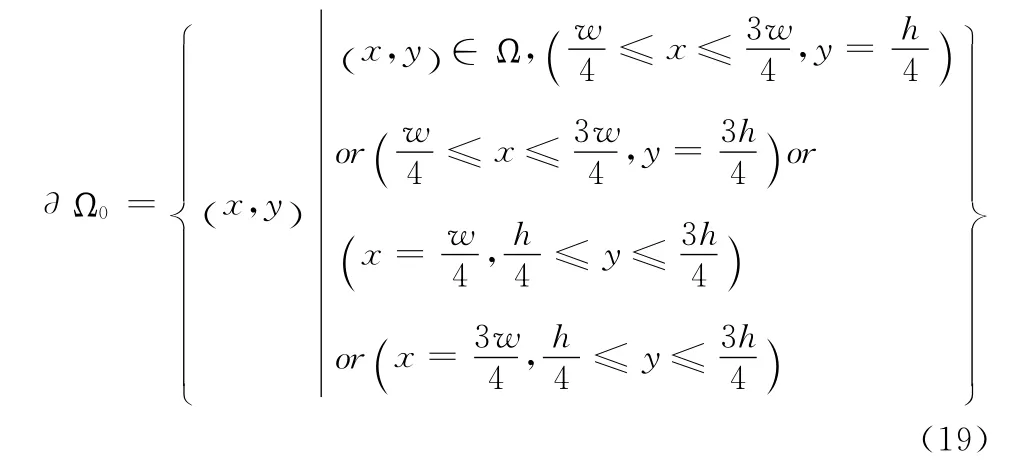
式中：w、h——图像的宽、高。

3 实验结果与性能评估

用仿真超声图像和临床淋巴癌超声图像为测试图像，对提出分割算法的有效性和普适性进行验证。实验中主要通过主观 “分割效果”和客观的区域面积误差参数和边界误差参数［9］评价算法的优劣。此外，将提出算法与经典的分割算法：Tsai［3］等人的算法，Li.Wang［8］等人的算法和Liu［9］等人的算法以及LBF［5］算法进行比较。本文算法与另外4种算法都是在实验平台为Matlab7.1，计算机配置为：Pentium （R）dual－Core E5400 2.70GHz CPU，1GB内存，Windows XP操作系统下进行仿真的。

3.1 仿真超声图像分割

图1是仿真超声图像的5种算法的分割结果。图1（a）是在原图上叠加了斑点噪声的仿真超声图像，斑点产生模型详见文献［10］。图1（b）～图1（f）分别是LBF 算法、Li.Wang等人算法、Liu等人的算法、Tsai等人算法和本文算法的分割结果，分割轮廓用红色线标注。由图1可以看出本文算法得到较精确的分割结果。图1（b）和图1（c）两种算法受噪声影响无法得到目标轮廓。图1（d）和图1（e）的分割结果因受噪声影响，在迭代次数达到1000次时曲线仍无法完全演化至目标边界导致得到的轮廓有较大误差。

图1 仿真超声图像分割

3.2 临床超声图像分割

临床超声图像采集自Philips Envisor 2540A 超声设备，由昆明医科大学第三附属医院提供，在得到病人许可后使用。

图2是提出方法对乳腺超声图像的分割结果，图2（a）是初始轮廓，图2（b）～图2（f）分别是提出分割算法经过100，200，300，400和500次迭代后的分割结果，从图中可看出，经过500次迭代后，将目标区域较完整地分割出来。

图3是淋巴癌1的算法分割结果与医生标注区域轮廓的比较。图3（a）为医生标注的淋巴癌轮廓。图3（b）～图3（e）分别为LBF算法、Li.Wang算法、Liu算法和Tsai算法的分割结果，分割轮廓用红色线标注。从图中可看出，图3（b）和图3（c）容易受到噪声的影响，检测出虚假边缘，无法得到准确的目标轮廓。图3（d）和图3（e）算法得到的曲线无法演化至目标轮廓。相比较而言，本文算法虽然检测出部分虚假边缘，但是得到的目标轮廓与医生标注的目标区域非常接近。

图2 乳腺超声图像分割结果

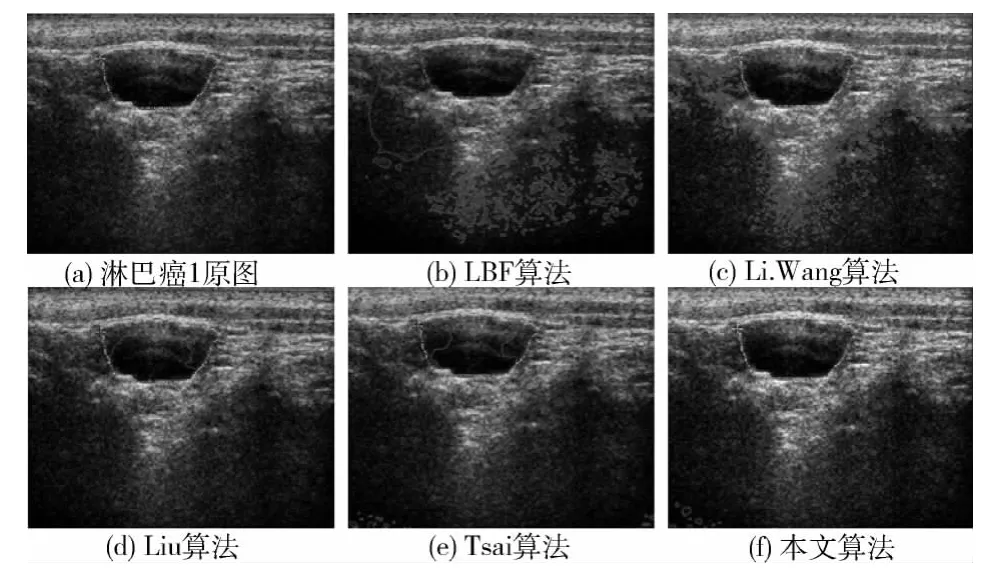
图3 淋巴癌1分割算法产生的区域与医生标注轮廓的比较

图4是淋巴癌2的算法分割结果与医生标注轮廓的比较。图4（a）为医生标注的淋巴癌轮廓。图4（b）～图4（e）分别为LBF算法、Li.Wang算法、Liu算法和Tsai算法的分割结果。由图3可以看出，图（b）和图（c）的分割结果受斑点噪声的干扰，无法得到准确的目标轮廓，检测出许多虚假边界。图（d）的分割结果得到的曲线明显比医生勾画的小。图（e）得到了较接近医生标注的轮廓，但在左下角处检测出虚假轮廓。相比较而言，提出算法图（f）更接近医生的标注区域轮廓，而且分割结果没有包括虚假边缘。

图4 对淋巴癌2分割算法产生的区域与医生标注区域轮廓的比较

图5是淋巴癌3的算法分割结果与医生标注区域轮廓的比较。图5（a）为医生标注的淋巴癌轮廓。图5（b）～图5（e）分别为LBF算法、Li.Wang算法、Liu算法和Tsai算法的分割结果。由图4可以看出，图（b）和图（c）的结果检测出了许多的虚假边界，无法得到准确的分割结果。图（d）的分割结果与医生标注的区域相差较大，图（e）的轮廓较接近医生标注的轮廓，但仍检测出少许虚假轮廓。相比较而言，提出算法图（f）提取的轮廓更接近医生的标注区域轮廓，而且没有包含多余的虚假边缘。

图5 对淋巴癌3分割算法产生的区域与医生标注区域轮廓比较

3.3 客观分割结果比较

为客观比较提出分割算法的合理性，采用区域面积误差参数和边界误差参数［9］作为指标，对本文算法与另外4种对照算法的分割结果与医生标注的病变区域轮廓进行定量比较，判定分割结果的准确性。

3.3.1 区域面积误差参数

刘等［9］提出用区域面积误差评估有多少病变区域被生成的病变区域正确或是错误覆盖。TP 表示真阳性的面积比，FP 表示假阳性的面积比，FN 表示假阴性面积比和SI表示相似性面积比。计算方法如下

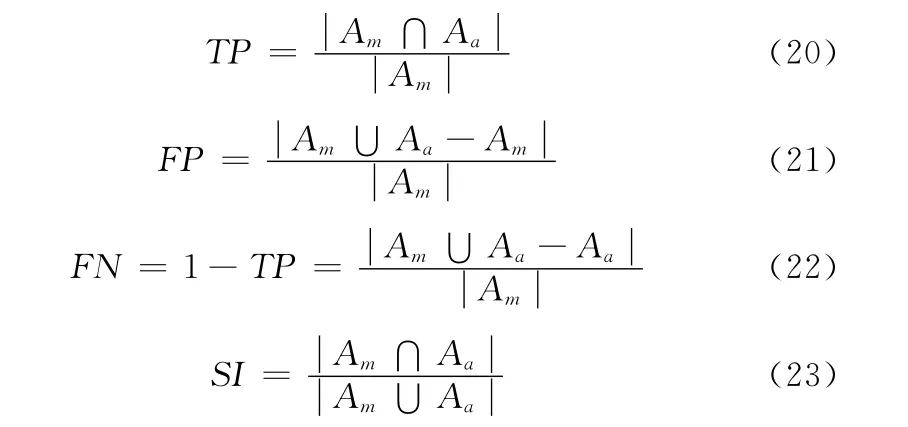
式中：Am——真实轮廓或医生手动画出的病变区域的像素集合。Aa——分割算法生成的病变区域像素集合。当TP百分比较大时，更多的病变区域被生成的病变区域覆盖。当FP 百分比较小时，较少的非病变区域被生成的病变区域覆盖。当SI 百分比较大时，生成的区域更相似于医生手工画的区域。

3.3.2 边界误差参数

本文使用 Hausdorff 距离（HD）和绝对平均距离（MD）［9］两个边界误差指标分析由分割算法自动得到的轮廓与放射科医生手画的轮廓差异对比，HD 是两轮廓之间最大误差，MD 是两轮廓的平均误差，HD 和MD 越小说明分割的结果越好。

设定真实的或医生勾画的边界和算法分割的边界分别为Q ＝ ｛q1，q2，…，qr｝和P ＝ ｛p1，p2，…，pu｝，qr和pn分别是Q 和P 轮廓上的点。则轮廓P 上的点到轮廓Q 的最短距离为

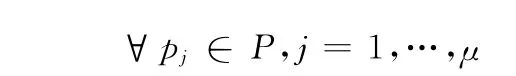
式中：‖·‖ ——二维的欧氏距离。HD 和MD 定义为

式中：γ、μ——轮廓Q 和P 边界像素的数量。HD 和MD 的一致性规范为

提出算法与4种对比算法的区域面积误差参数和边界误差参数比较见表1。

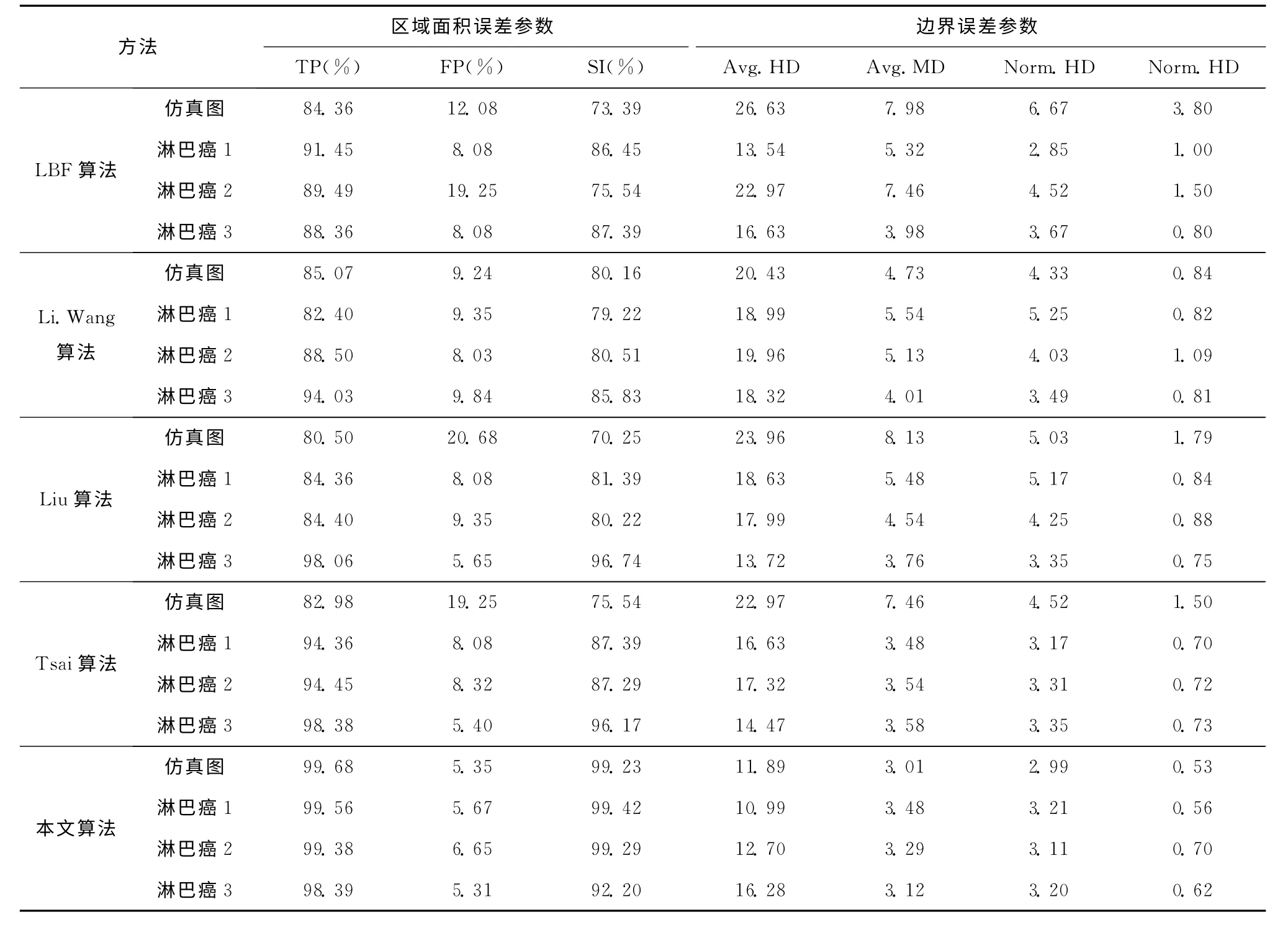
表1 本文算法与另外4种算法的客观指标比较

由表1知，本文的算法得到的TP 和SI 百分率比其它4种算法得到的更高，而Hausdorff距离和边界误差参数比对比算法得到的低，说明本文算法分割的轮廓比其它算法得到的轮廓更接近于真实的目标轮廓或医生勾画的轮廓。

4 结束语

本文提出了一种新的超声图像分割算法。提出算法根据不同的区域的均值和方程建立其能量函数。提出算法充分利用了全局变量驱使能量最小化，实现了无需人工干预的自动分割。将提出算法用于含有斑点噪声的仿真超声图像和临床超声图像进行分割测试，并与经典的基于活动轮廓模型的分割算法进行主客观评价，实验结果表明：提出算法有较好的分割性能，验证了算法的有效性和普适性。

［1］Li C，Xu C，Gui C，et al.Distance regularized level set evolution and its application to image segmentation ［J］.IEEE Transaction on Image Processing，2010 （19）：3243－3254.

［2］Mao H，Liu H，Shi P.Neighbor－constrained active contours without edges ［C］／／Anchorage，Alaska，USA：CVPR，2008：1－7.

［3］Tsai A，Yezzi A，Willsky AS.Curve evolution implementation of the mumford－Shah functional for image segmentation，denoising，interpolation and magnification ［J］.IEEE Transaction on Image Processing，2001，10 （8）：1169－1186.

［4］Li C，Kao C，Gore J，et al.Implicit active contours driven by local binary fitting energy ［C］／／Washington，DC，USA：CVPR，2007：1－7.

［5］Li C，Kao C，Gore J.Minimization of region－scalable fitting energy for image segmentation ［J］.IEEE Transaction on Image Processing，2008，17 （10）：1940－1949.

［6］Brox T.From pixels to regions：Partial differential equations in image analysis［D］.Germany：Saarland University，2005.

［7］Chan TF，Vese L.Active contours without edges［J］.IEEE Transaction on Image Processing，2001，10 （2）：266－277.

［8］Wang L，Li C，Sun Q.et al.Brain MR image segmentation using local and global intensity fitting active contours／surfaces［J］.Med Image Comput Comput Assist Interv，2008，11 （Pt 1）：384－392.

［9］LIU B，Cheng HD，Huang J，et al.Automated segmentation of ultrasonic breast lesions using statistical texture classification and active contour based on probability distance ［J］.Ultrasound in Medicine Biololgy，2009，35 （8）：1309－1324.

［10］Laporte C，Clark JJ，Arbel T.A fractal multi－dimensional ultrasound scatter distribution model［C］／／Arlington，Virginia，USA：4th IEEE International Symposium on Biomedical Imaging，2007：880－883.