基于Mean Shift重要性采样的粒子滤波跟踪算法

刘 璞，王春平，徐 艳

（军械工程学院 电子与光学工程系，河北 石家庄050003）

0 引 言

粒子滤波因其在非线性、非高斯系统中具有较强的鲁棒性［1］，已经被应用于复杂情况下的目标跟踪，并且取得了良好的效果。但是粒子滤波算法仍存在一些缺陷，主要表现为两个方面［2］：一是在粒子递推的过程中，部分粒子的权值趋向于1，其它粒子的权值趋向于0，形成了粒子的退化现象，使粒子集无法准确近似系统状态的统计特性；二是为了提高粒子滤波算法的精度，往往采用大样本量，这样虽然精度提高了，但是增大了算法的计算量，影响目标跟踪的实时性。

粒子滤波能否取得好的效果很大程度上取决于粒子的传播方式，即重要性采样的设计，这是粒子滤波领域的一个研究热点［3］。结合上述问题，本文提出了基于MS重要性采样的粒子滤波跟踪算法，该算法将MS算法融入到粒子滤波算法中，利用MS的迭代寻优过程对粒子样本进行确定性搜索，使其收敛到局部最优点，完成粒子的重要性采样，同时能够增大有效粒子权重，减少跟踪过程采用的粒子数目，降低计算量，提高跟踪的实时性。

1 Mean Shift算法

Mean Shift算法是一种非参数核函数估计方法［4］，在采样充分的情况下，核函数估计能够逐渐收敛于服从任意分布的密度函数，将以每个采样点为中心的局部区域的平均效果作为该采样点的概率密度估计值，最终综合所有采样点的密度估计结果，实现对目标位置的稳定预测［5］。

目标的颜色特征对于目标的尺度、旋转或者变形具有较好的稳定性［6］，因此采用颜色直方图表达目标特征有助于目标的稳定跟踪［7］。本文根据MS 算法的核函数概念，利用目标颜色分布建立目标模型。核函数采用Epanechikov核函数

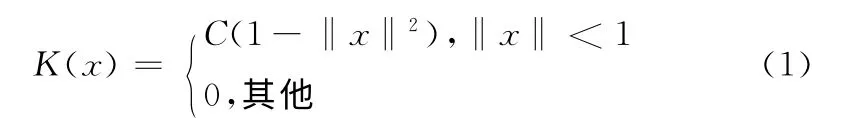
假设目标区域的中心为x0，目标区域内的像素点用｛xi；i＝1，2，…N ｝表示，彩色图像的每个颜色通道的特征值为u＝1，2，…M，对目标区域进行建模

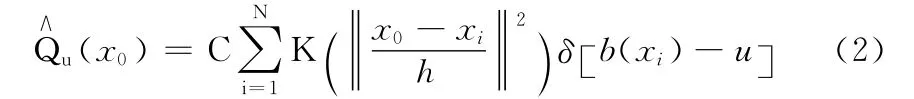
式中：δ——Delta函数，C——常量系数，满足

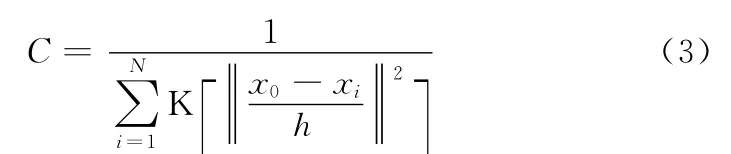
假设候选区域的中心为y0，根据式（2）可以同理得出，候选区域的目标模型为

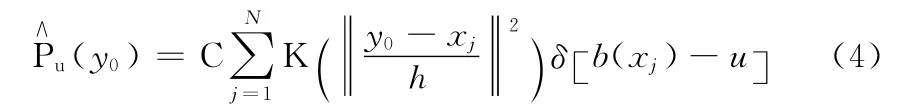
将候选区域的颜色分布与参考模板的颜色分布进行对比，利用Bhattacharyya系数作为度量二者相似性的标准，其函数表达式为

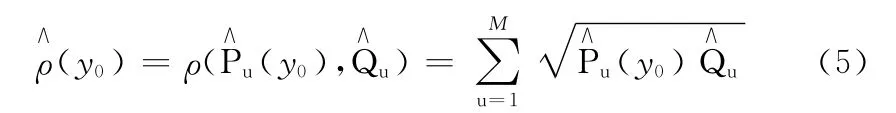
在候选区域进行MS确定性搜索时，使ρ∧（y0）取得最大值的位置即是目标的新位置。假设给定目标的起始位置为y0，根据MS算法的收敛性，进行有限次迭代后找到其新位置y1

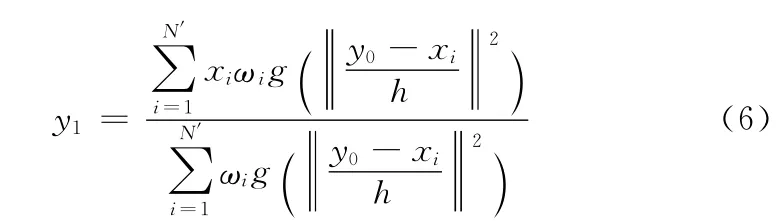
式中：ωi——采样点的权值，g（x）——核函数，g（x）＝－K′（x），h——核函数的带宽。

设定阈值ε作为判断迭代是否停止的条件，当‖y1－y0‖＜ε时，表明已经找到局部最优点，此时终止MS迭代过程。

2 改进的粒子滤波算法设计

粒子滤波是一种非参数化的基于贝叶斯随机采样的滤波方法［8］，适用于非线性系统，其主要思想是利用状态空间中一系列随机样本粒子的加权对系统状态的后验概率密度进行近似，得到系统状态的估计值［9］。

假设系统的状态方程和观测方程分别为

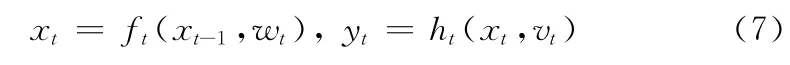
式中：ft（）、ht（）——状态转移函数、量测函数，wt、vt——系统噪声、观测噪声。

t时刻观测量的集合用Dt表示

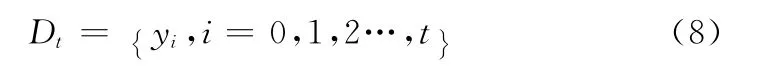
为减弱粒子退化现象和降低算法计算量，将MS算法嵌入到PF的重要性采样中，利用MS算法对粒子的收敛作用，使得MS重要性采样后的粒子更加接近目标的真实状态分布，这样既能够减弱粒子的退化又一定程度上减少对粒子的需求量，降低算法计算量。

算法的具体设计如下：

（1）初始化目标区域。在第一帧图像中用鼠标画取目标区域，根据颜色分布建立目标参考模型，在选取的先验概率分布函数P（xt－1）中抽取N 个粒子，i＝0，1，2…，N，令每个粒子的权重为N－1。

（2）对每个粒子利用UKF（无迹卡尔曼滤波）算法［10］得到和，其建议分布函数为

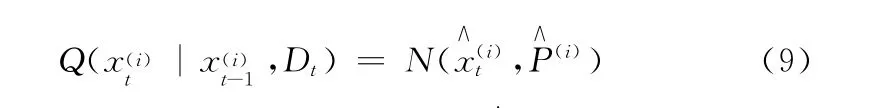
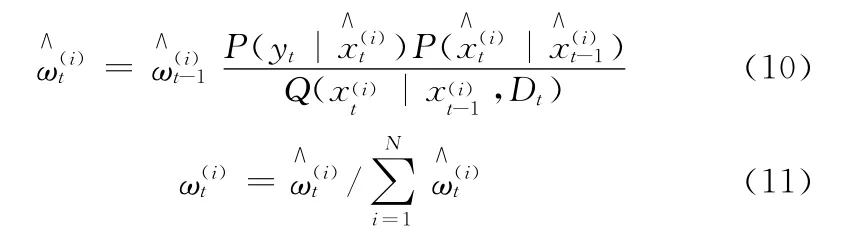
（5）估计目标位置。输出估计值P（xt｜Dt）

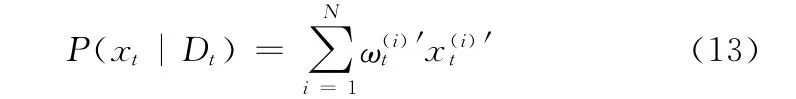
（7）令t＝t＋1，重复步骤（2）～（6）。

综合以上步骤，本文算法流程如图1所示。

3 仿真实验与分析

实验用的PC机配置为奔腾双核，主频2.5GHz，内存2.0GB；软件工具为Windows XP 操作系统，MATLAB R2011运行环境。

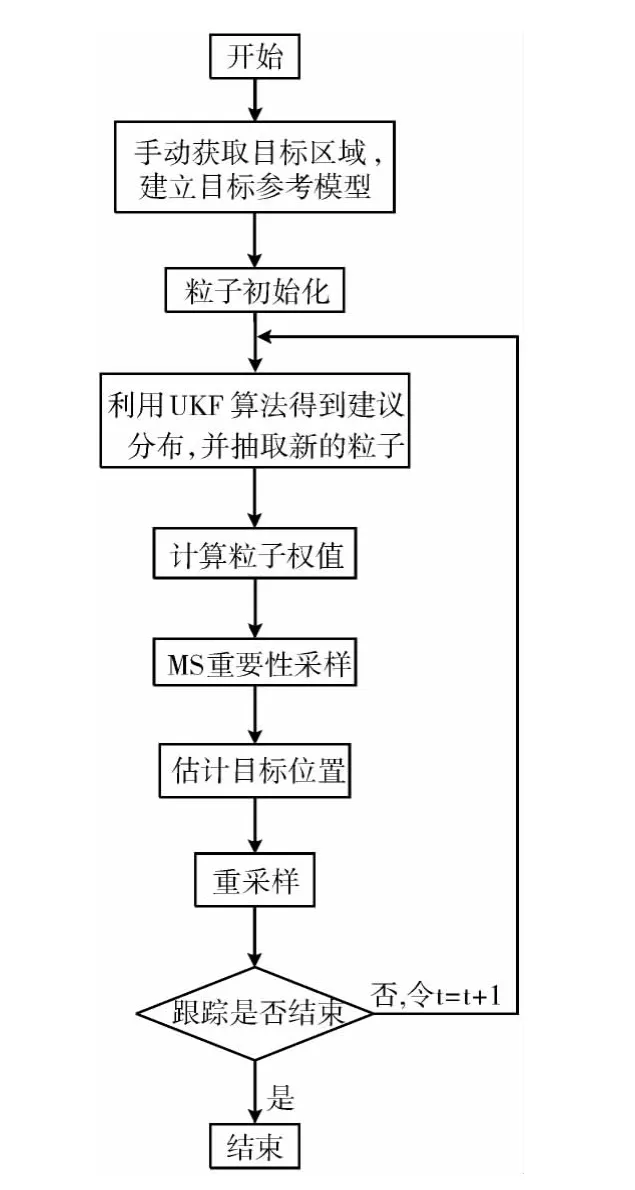
图1 本文算法流程

首先对传统粒子滤波算法和本文算法进行粒子模拟跟踪仿真，如图2所示，其中图2（a）是模拟的目标位置真值，图2（b）是传统粒子滤波算法的跟踪结果，图2（c）是本文算法的跟踪结果。将图2（b）和图2（c）进行比较可以看出，传统算法由于少数粒子占据了大部分权重，重采样后粒子的多样性减少，粒子退化严重，导致不能准确估计目标位置，跟踪效果较差；本文算法由于在重采样之前进行了MS重要性采样，对目标位置进行确定性搜索，保证了粒子状态估计的准确性，跟踪效果较好且与图2（a）的真值相近。

选取路面行驶汽车的视频序列（720 576，25 帧／s）和直升机模型空中飞行的视频序列（600 460，25 帧／s），都采用传统粒子滤波算法和本文提出的滤波算法分别进行跟踪测试。

图3是背景保持不变的汽车行驶序列跟踪结果，由上至下分别是第10、48、85帧图像。图3（a）是传统粒子滤波算法的跟踪结果，传统算法在跟踪过程中对目标位置的估计稍有偏差，不过序列中目标颜色与背景对比度较大且背景保持不变，一定程度上降低了粒子退化的速度，使候选模型和目标参考模型仍然比较接近，有一定的跟踪效果。图3（b）是本文算法的跟踪结果，算法中加入了MS重要性采样，对粒子的确定性搜索使粒子样本更加接近目标的真实状态，由第85 帧图像可以看出，其跟踪效果优于传统算法。

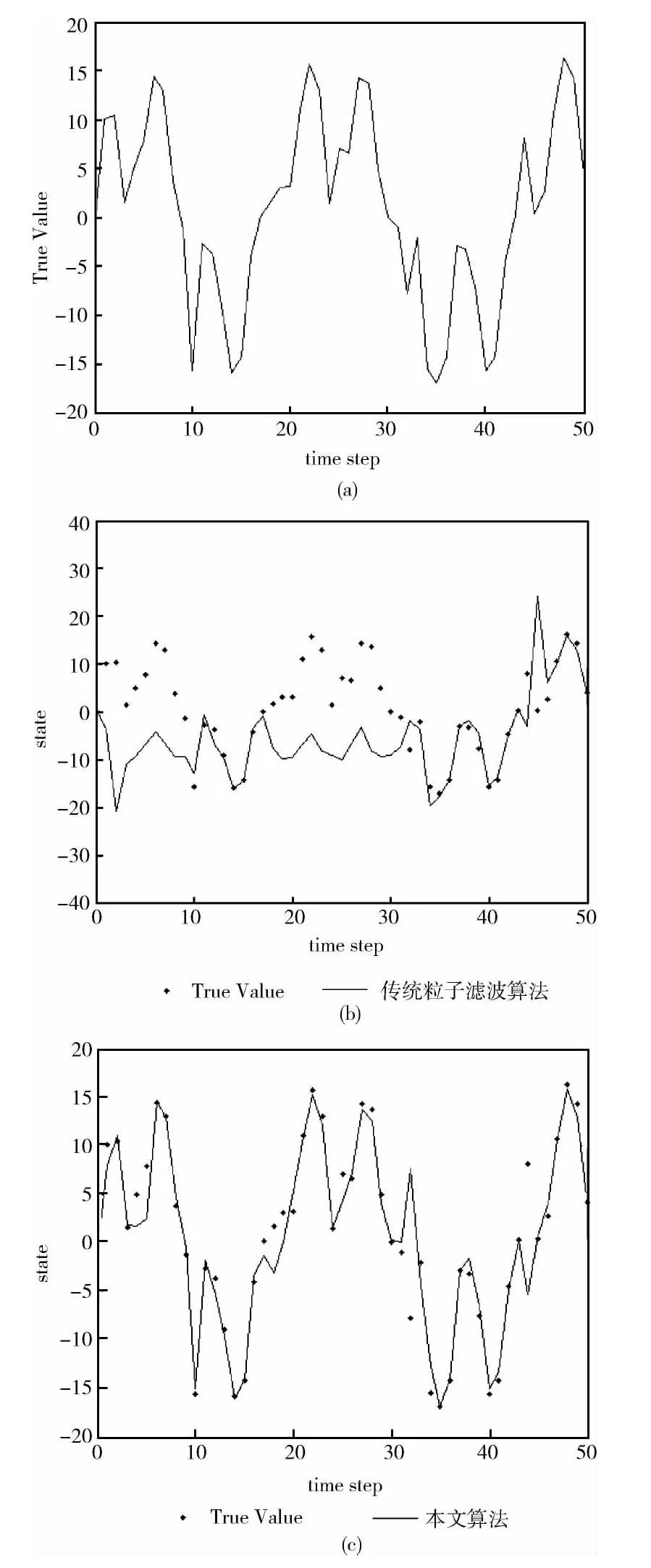
图2 传统粒子滤波和本文算法跟踪仿真对比结果

图4是背景由简单变复杂的直升机飞行序列的跟踪结果，由上至下分别是第30、79、105帧图像。图4（a）是传统粒子滤波算法的跟踪结果，传统算法由于在粒子递推过程中大部分权重集中在少数粒子，重采样后粒子多样性减少，出现粒子退化现象，尤其当背景变复杂且与目标颜色相近时，粒子样本的估计状态与目标真实状态差别较大，导致跟踪效果较差，特别是在第107帧图像中，目标已经基本丢失。图4（b）是本文算法的跟踪结果，由于对建议分布中抽取的粒子进行了MS重要性采样，使大部分粒子收敛到局部最大值，粒子样本的估计状态接近于目标的真实状态，虽然背景变得复杂且目标颜色与背景近似，但是对跟踪效果的影响较小，到第107帧图像时，仍然能够准确跟踪目标。

图3 汽车序列跟踪过程

图4 直升机序列跟踪过程

4 结束语

本文针对粒子滤波目标跟踪中粒子退化的问题，将MS算法融入到粒子滤波算法中，提出了基于MS重要性采样的粒子滤波目标跟踪算法。该算法利用目标颜色分布建立目标参考模型，在MS的迭代寻优过程中，对粒子样本进行确定性搜索，使其收敛到目标候选模型的局部最优点，以更加准确地估计目标状态，实现对目标模型的重要性采样，有效解决了粒子退化问题。同时粒子估计准确性的提高，也减少了算法对粒子的需求量，增强了目标跟踪的实时性。实验结果表明，该算法的跟踪性能优于传统的粒子滤波算法，特别在背景较复杂且与目标颜色相近的情况下，跟踪优势更加明显。

［1］LIU Yiming，ZHOU Shangbo.Video tracking algorithm of particle filtering based on multi－feature fusion ［J］.Computer Engineering，2010，36 （22）：228－230 （in Chinese）. ［刘一鸣，周尚波.基于多特征融合的粒子滤波视频跟踪算法 ［J］.计算机工程，2010，36 （22）：228－230.］

［2］HAN Hua.The research on intelligent multiple video targets tracking based on improved particle filter ［D］.Shanghai：PhD Thesis of DongHua University，2011：25－26 （in Chinese）.［韩华.基于改进粒子滤波算法的多目标智能视频跟踪研究 ［D］.上海：东华大学博士学位论文，2011：25－26.］

［3］GAO Jianpo，WEI Zhihui，MENG Yingjun，et al.Improved CONDENSATION face tracking algorithm based on mean－shift drift［J］.Opto－Electronic Engineering，2009，36 （2）：137－142 （in Chinese）.［高建坡，韦志辉，孟迎军，等.基于均值移动确定性漂移的改进CONDENSATION 人脸跟踪 ［J］.光电工程，2009，36 （2）：137－142.］

［4］Ning Jifeng，Zhang Lei.Scale and orientation adaptive mean shift tracking［J］.IET Computer Vision，2012，6 （1）：52－61.

［5］GONG Yisong，GUI Qingming，LI Baoli，et al.Design of particle filtering algorithm based on mean shift and its application in navigation data processing ［J］.Journal of Surveying and Mapping，2011，40 （Suppl.）：120－125 （in Chinese）.［宫轶松，归庆明，李宝利，等.基于均值漂移的粒子滤波算法设计及其在导航数据处理中的应用 ［J］.测绘学报，2011，40 （增刊）：120－125.］

［6］ZHENG Yufeng，MA Xiurong，ZHAO Xiaolin，et al.Mean shift target tracking algorithm based on color and edge features［J］.Journal of Optoelectronics· Laser，2011，22 （8）：1231－1235 （in Chinese）.［郑玉凤，马秀荣，赵晓琳，等.基于颜色和边缘特征的均值迁移目标跟踪算法 ［J］.光电子·激光，2011，22 （8）：1231－1235.］

［7］Leichter I，Lindenbaum M，Rivlin E.Mean Shift tracking with multiple reference color histograms［J］.Computer Vision and Image Understanding，2010，114 （3）：400－408.

［8］Vasileios Maroulas，Panos Stinis.Improved particle filters for multi－target tracking ［J］.Journal of Computational Physics，2012，23 （1）：602－611.

［9］GUO Xiaosong，LI Yipeng，GUO Junbin.Research on particle filtering algorithm and its applications［J］.Computer Engineering and Design，2009，30 （9）：2264－2266 （in Chinese）.［郭晓松，李奕芃，郭君斌.粒子滤波算法及其应用研究［J］.计算机工程与设计，2009，30 （9）：2264－2266.］

［10］Wu Chunlin，Han Chongzhao.Quadrature Kalman particle filter［J］.System Engineering and Electronics，2010，21（2）：175－179.