基于SL0算法的快速局部稀疏多径信道估计

刘 婷，周 杰，2＋

（1.南京信息工程大学 电子与信息工程学院，江苏 南京210044；2.日本国立新泻大学 工学部电气电子工学科，新泻950－2181）

0 引 言

未来无线移动通信在数据传输速率、系统性能以及系统容量等方面的要求日益增长，目前已由传统的单输入单输出系统（single input single output，SISO）发展到多输入多输出（multi input multi output，MIMO）系 统。采 用MIMO多天线发送和接收技术，可用充分利用空间分集的方法在空间域上获得更大的信道容量增益，从而满足高传输速率、高传输性能以及高频谱利用率［1］。MIMO 系统接收信道均衡和相关检测都需要精确的信道状态信息（channel state information，CSI）。所以，信道估计已经成为一个重要的研究方向。只有对CSI的准确估计，才能够进一步研究时延，多普勒频移以及相关衰落的空间多样性［2］。现在一般采用基于训练序列的多径信道估计方法［3］，这样接收端可以及时掌握信号的数据量、频率等有效信息，从而更好地获知CSI信息。传统的信道估计方法，均假定无线多径信道是密集型的，导致频谱利用率低。随着研究的逐步深入，可以发现无线信道的稀疏性［4］，所以挖掘稀疏信道的特性并加以利用可以大大提高频谱资源的利用率。现已在图像处理、数据压缩、雷达等领域得到广泛应用［5］。研究表明，之前关于信道的估计一般都是假定信道是纯密集型或纯稀疏型信道，但是在实际信道估计时，往往都是混合型信道，即局部稀疏信道。局部稀疏信道由两部分组成，一是密集型冲激响应，二是稀疏型冲激响应。密集型冲激响应是由很多密集的非零抽头系数组成的，而稀疏型冲激响应只有很少的非零抽头系数，绝大多数抽头系数为零［6］。基于以上研究，本文采用局部稀疏信道模型，同时结合最优化SL0算法［7］，对信道状态信息进行了相关估计，分析了信噪比（signal noise ratio，SNR）、迭代次数、信道的压缩程度对重构原始信号误差的影响。随后文中分析了SL0算法与其它相关算法的重构信号匹配度以及运算时间的大小，并通过数值仿真得到了验证。研究结果表明快速平滑的L0（SL0）算法，可以很好地对稀疏信道进行估计。SL0算法准确度高，计算复杂度低，对噪声不敏感，速度快，具有较好的鲁棒性。所以，在实际信道估计中，采用SL0 算法，能够高效精确地获知CSI，从而能够精确重构出原始信号。

1 压缩感知

1.1 压缩感知理论

压缩感知的思想就是对稀疏信号以远低于奈奎斯特采样定律要求的频率进行全局测量，将采样和压缩合二为一，然后选取重构算法把压缩信号恢复成原始信号。假定y＝［y（1），y（2），y（3），…，y（N）］T是一维离散信号，并且可用正交基组 ｛φi｝Ni＝1表示为

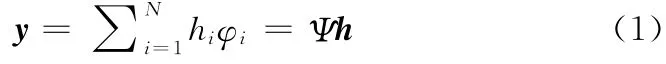
式中：h——y关于正交基的权重系数向量，若h 中只有K（K＜＜N）个系数远大于零，其余系数都近似为零，则认为h具有稀疏特性。

1.2 信号重构

根据以上介绍可知，h是Ψ 基下的K 稀疏信号，通过M（M＜＜N）个不同的观测向量 ｛｝mj＝1对信号压缩处理，计算h和每个观测向量的内积从而得到观测值，由于M＜＜N，这就得到了压缩信号s

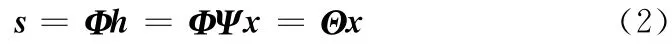
但是由于h的K－稀疏性，可以采用适当的重构算法得到稀疏解＾h，进而得到估计信号＾x，可表示如下

1.3 测量矩阵的设计

一个非常重要的设计原则就是Θ 要满足RIP （限制等距）性 质［8］

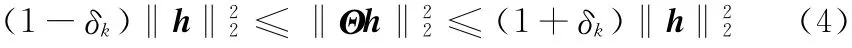
当δi＜1，则认为矩阵Θ 满足限制等距条件，这就使得K－稀疏信号h 的欧氏距离保持不变，防止h 在Θ 的零空间中，出现无穷解的情况。并且，随着δi的减小，恢复出原始信号的失真程度也就越低。

1.4 压缩感知算法研究

Candes等人证明了信号的重构可以通过转化为求解最小L0范式问题来获取h的精确或近似逼近，从而恢复信号

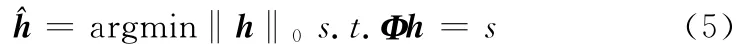
式中：‖h‖0——h的0阶范数，即h中非零元素的个数。

现在关于压缩感知的算法主要有三大类：松弛方法、贪婪方法、非凸方法。以BP算法为代表的松弛方法，计算复杂度较高，稀疏系数位置不明确。贪婪算法，以（MP，OMP）［9］最为典型，在信噪比较高时，可以获得较好的MSE估计性能，但在信噪比不高的情况下，估计效果非常不稳定。非凸方法，迭代重加权LS算法和FOCUSS算法，算法计算量相对简单，但是只有在待估计变量的稀疏度较高时，才能保证估计结果的准确性。

对于线性欠定系统方程（2），本文采用的信道估计算法，是基于过完备稀疏分解的，能直接最小化L0范数。这个方法在求解稀疏解时更加快速，估计精度高，计算量低；并且对信噪比SNR 的变化不敏感，可以获得稳健的稀疏估计量。

2 局部稀疏信道模型

假定训练序列s（n）是服从高斯随机分布的，h（n）表示稀疏信道冲激响应，训练序列通过稀疏信道后，在接收天线处，得到采样数据样本y（n）为

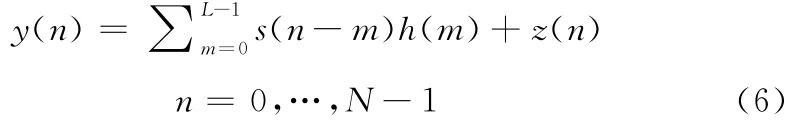
式中：m——稀疏信道响应延迟，z（n）——零均值的圆对称加性白高斯噪声，式（7）用矩阵形式表示如下

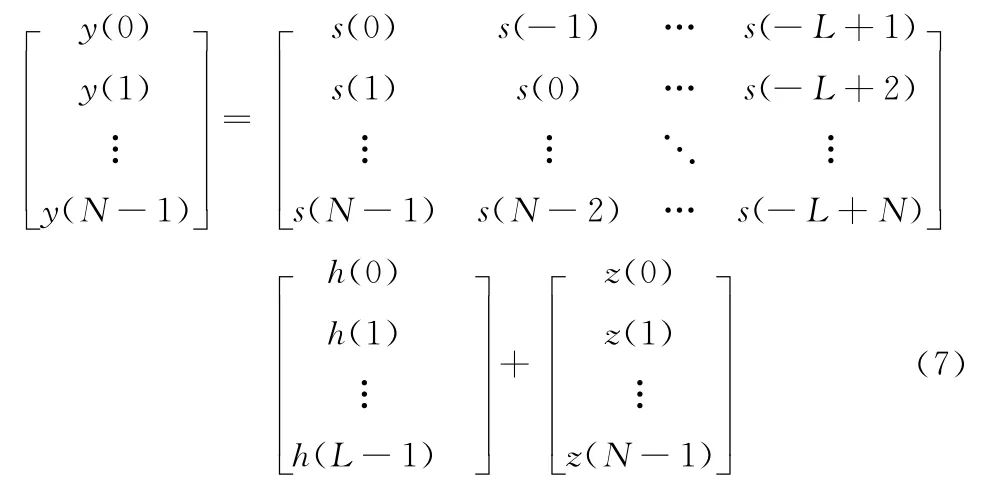
缩写形式为y＝SH＋Z。S 是Toeplitz矩阵，能够满足RIP性质［10］。在实际信道估计中，有些直达波可能会先行到行程密集的脉冲，而经过多次散射和反射的波，由于衰减等原因，会导致信道的稀疏性。从而我们可以得到局部稀疏多径信道的一般表达式为h＝［hd，hs］T，hd代表Ld×1维的密集信道冲击响应，hs代表（L－Ld）×1维的稀疏信道冲击响应，二者构成了本文所提出的局部稀疏信道

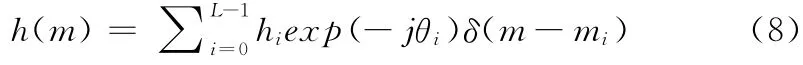
式中：hiexp（－jθi）——信道系数，Δm——采样率，信道长度L＝mmax／Δm，信道稀疏度K＝｛｜hi｜＞0，i∈L｝。

本文采用的局部稀疏信道模型如图1所示，密集型冲击响应由很多非零抽头组成，稀疏型冲击响应只有为数不多的非零抽头，二者共同组成了局部稀疏信道。同时非零信号的冲激响应是以近似聚类的形式分布的。

图1 局部稀疏信道冲击响应采样

假设信道h由C 个块状冲击响应级联构成，每块包含d 个信道抽头，则局部稀疏信道h可表示如下

式中：L＝Cd。由于信道中不可避免会存在噪声，所以本文扩展到有噪环境下进行考虑，从而信道h 的稀疏测量可表示为以下形式

其中

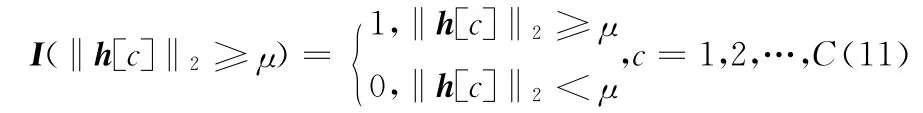
式中：μ——噪底，在噪声环境下，通过观测超过噪底的冲激响应，就可得到局部稀疏信道的稀疏度。

3 快速平滑的SL0信道估计算法

由于高斯函数的可分辨性，本文采用零均值高斯函数来定义信道H，定义如下

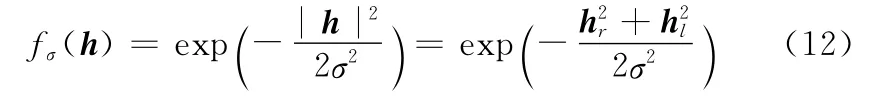
由文献 ［11］可知，基于压缩感知的最优局部稀疏信道估计可由以下式子表示

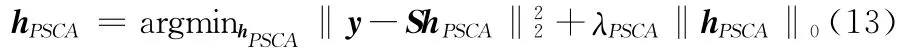
正则化系数λPSCA＞0，是两项的权重

由此可以规定

从而可将信道h的L0范式的平滑估计转化为关于函数u的平滑估计研究。

定理 稀疏信道估计：Fσ（h）取最大值，s.t.y＝XH＋Z。

（1）当σ →∞，代表y＝XH＋Z 的L2范式估计，此时h＝XH（XXH）－1y；

（2）当σ→0，代表y＝XH＋Z 的L0范式估计。

基于以上定理，采用SL0进行稀疏信道估计。

输入：训练序列X，接收信号y，信道方差递减序列σ＝｛σ1，…，σk｝，信道的初始估计值‖hPSCA‖0。

输出：稀疏信道估计值hPSCA。

——初始化

y＝XH＋Z 中信道L2范式的最小逼近，此时信道可以通过伪逆的形式表现出来。

选择σ的适当递减序列σ＝｛σ1，…，σk｝。

——当k＝1，…，K；

（1）令σ＝σk；

（2）采用最速下降法，得到Fσ（h）的最大值，即信道H的最小化估计。

·初始化：hPSCA＝uk－1

·当n＝1，…，N 时（循环L 次）：

2）令hPSCA←hPSCA－μΔhPSCA，μ是步长；

3）hPSCA←hPSCA－XT（XXT）－1（XHPSCA－y）；

（3）令uk＝hPSCA，

——最终结果可以表示为hPSCA＝un。

4 结果与分析

4.1 仿真环境设置

本文主要采用了LS，OMP，CoSaMP以及最优SL0对局部稀疏信道进行估计。信道服从频率选择性衰落，功率谱分布满足高斯分布。训练序列采用的是长度为100的复Toeplitz矩阵，信道长度为500，其中非零抽头的个数为20。

4.2 SL0算法的相关性能

如表1所示，随着迭代次数的增加，σ逐渐降低，SNR和匹配度Mat都逐渐增大，MSE 随之减小。实际的信道估计中，应选取适当的迭代次数和σ 值，以使SNR，MSE，Mat维持在一个较好的平衡状态。

4.3 信道估计性能分析

4.3.1 估计值与真实之间的MSE

本文在正则化系数λ 取不同值的情况下，对局部稀疏信道模型和纯稀疏信道模型做了比较分析。如图2 所示，较之于纯稀疏信道，局部稀疏信道的归一化均方误差更低。

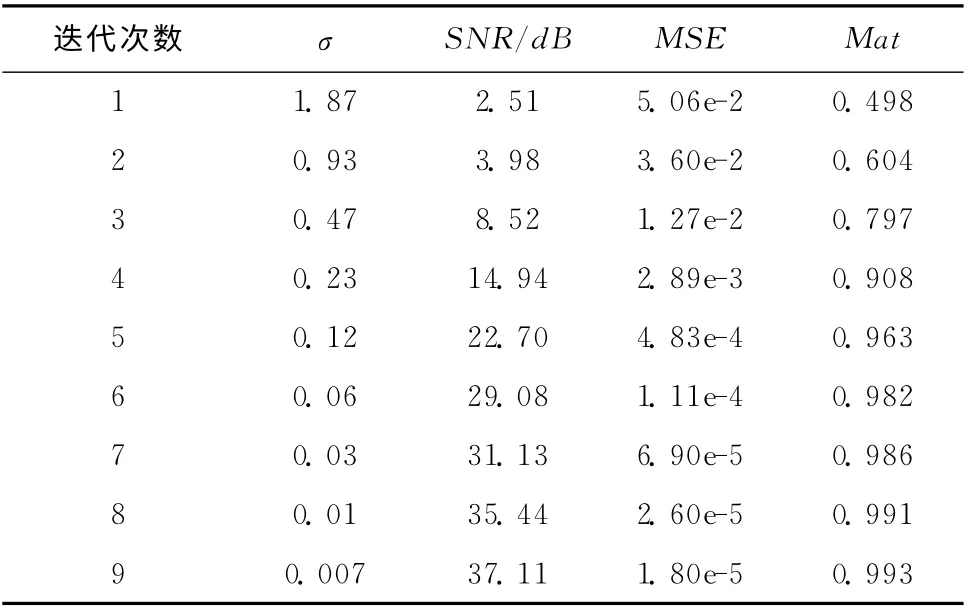
表1 SL0的相关性能图

图2 不同模型下的正则化系数λ－RMSE比较

同时，相比于OMP以及CoSaMP算法，SL0算法具有更好的MSE 性能。从图3 中可以看出，当信噪比超过15dB时，CoSaMP 的MSE 要明显低于OMP，精度较高。但是，和SL0相比，它们只是次优化的。SL0在整个SNR的比较范围内，都比OMP和CoSaMP两个算法的MSE 要低出很多，基本能够达到信号的精确重构。

图3 不同算法下的SNR－MSE 比较

4.3.2 MSE 的收敛性分析

本文采用的收敛性分析公式为

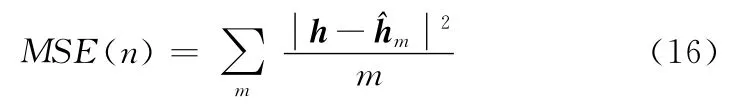
式中：m——试验次数，n——迭代次数。收敛性越好，可明显抑制噪声的干扰，提高系统的稳定度。

从图4中可以看出，在相同的迭代次数下，SL0算法的MSE 要明显低于LS，OMP 与CoSaMP，随着迭代次数的增加，SL0算法的收敛性能也远远优于LS，OMP 以及CoSaMP的收敛性能。在使用较少迭代次数的情况下，相比LS，OMP 和CoSaMP，SL0 能够取得相对更为精确的值。从而可以得到，SL0 算法对噪声不敏感，具有较强的抗干扰能力，估计量稳健。

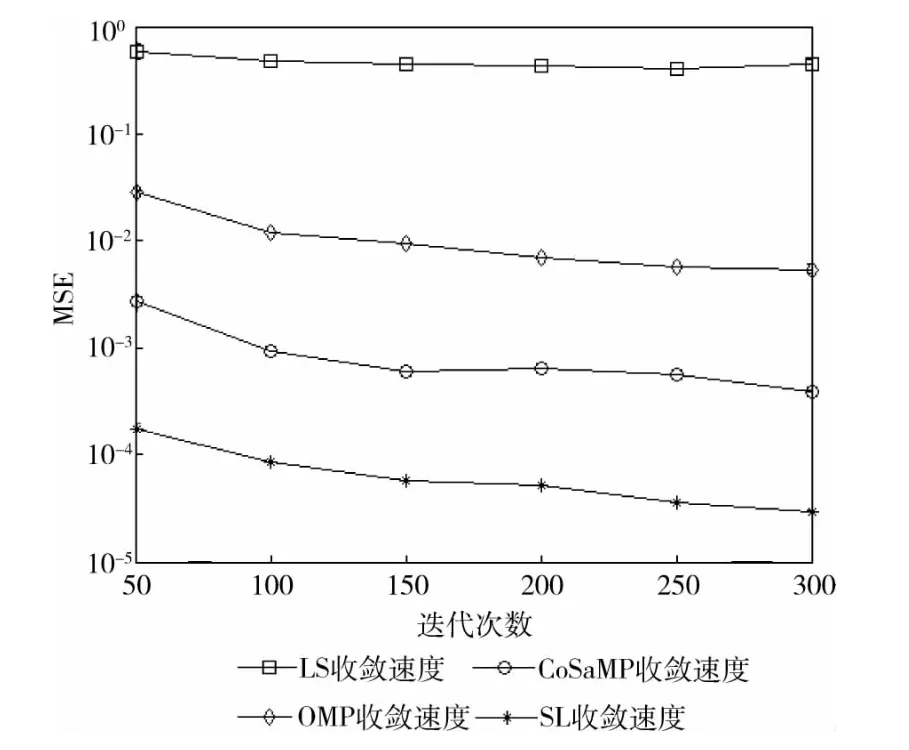
图4 算法收敛性比较

4.3.3 重构初始信号的匹配度分析

传统的信号重建质量衡量标准包括信噪比、误差等的分析比较。但是这些衡量标准并没有一个固定的范围，针对这种缺陷，本文采用一种新的重建质量的衡量标准，即匹配度（matching rate，Mat）

匹配度是一个介于（0，1）的值，当匹配度越接近于1时，说明重构信号和原始信号越接近。

图5中，随着c值的上升，匹配度呈上升趋势。同时，在压缩程度相同的情况下SL0 算法的匹配程度最高，当c值高于120时，匹配度Mat基本与1吻合，远远高于OMP和CoSaMP，可以完成信号的精确重构。特别在c 为145时，SL0的匹配度高达0.999986，而CoSaMP 的匹配度为0.879144，OMP的匹配度仅仅为0.2106。

4.3.4 重构精度分析

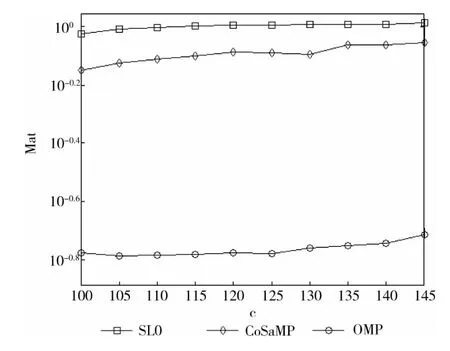
图5 不同压缩程度下的重构算法匹配度

假设观测矩阵是c×d 维的随机矩阵，c／d 为采样率。c值越小，压缩程度越大，对信号处理、存储、传输带来的好处也就相应增大。但是，压缩程度越大，接收端重构信号的难度也就随之增大，精确度也会有所降低，所以要根据实际信道情况选取适当的c值，以保证系统的性能。本文在讨论信号压缩程度时，系统采用的信噪比SNR 是20dB，其重构精度如图6所示。当c取110时，MSE 较小，基本可以重构出原始信号。但是，当c值继续降低时，整个系统的重构误差就会有所上升，所以本次实验环境，信号的极限压缩程度为110。在c值一定的情况下，SL0算法的MSE 最低，与原信号吻合度最高。

图6 不同压缩程度下的算法重构精度

4.3.5 算法的计算复杂度

本文通过计算4种算法的CPU 运算时间，可以得到各自的复杂度。尽管CPU 运算时间并不能完全反映各个算法进行信道估计的复杂度，但可以从中粗略得到算法的计算量。图7中，SL0算法在进行稀疏信道估计时，所用时间都维持在0.05s以下，而CoSaMP 算法的运算时间远大于0.2s，并且随着压缩程度的增大，有缓慢增加的趋势。至于OMP，计算时间要高于CoSaMP与SL0，同时计算时间随着c值的增大明显上升，这就增加了系统的负担。而LS算法的复杂度虽然较低，但是误差很大，信号恢复效果不是很理想。

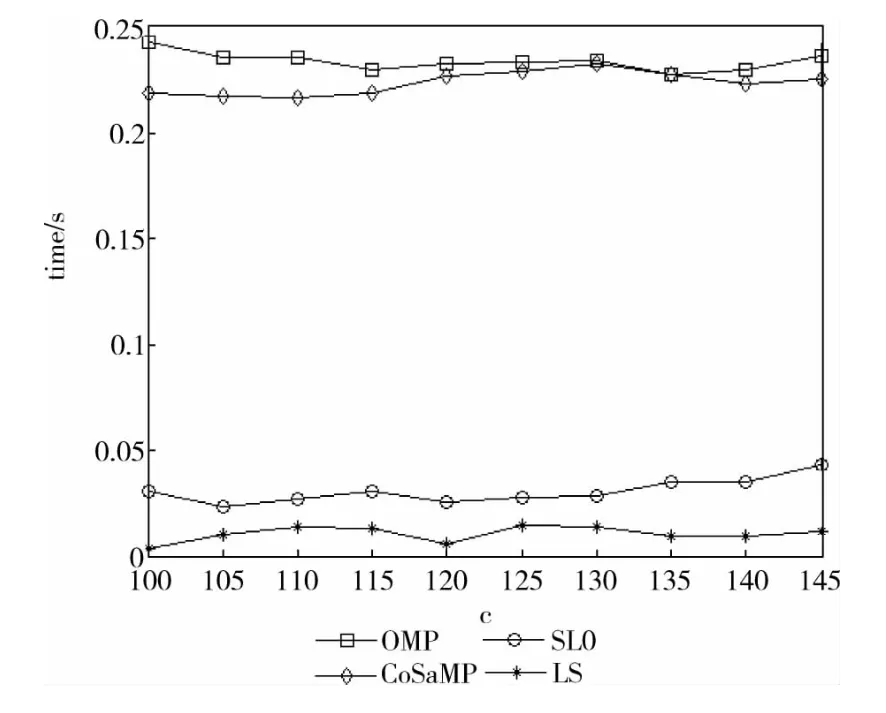
图7 计算复杂度比较

可以看出，对于基于压缩感知的局部稀疏信道估计，采用SL0算法的计算复杂度要比其它算法低很多，节约了时间，提高了整个系统的效率。

5 结束语

本文对局部稀疏信道进行了详细的分析与估计。不同于纯密集型信道或者纯稀疏型信道，局部稀疏信道能够更精确地恢复出初始信号中的信息。另外，采用新颖的SL0算法，充分利用稀疏信道的稀疏特性，获得了较好的信道估计效果。相比较于LS，OMP，CoSaMP，SL0 算法具有更好的估计精度，与原信号匹配度高，计算量低，时间快，对噪声不敏感，同时估计量稳健，具有很好的鲁棒性。

［1］Yen Chih Chen，Su Yu T.MIMO channel estimation in correlated fading environments［J］.IEEE Transactions on Wireless Communications，2010，3 （9）：1108－1119.

［2］Di Renzo M，Haas H.Space shift keying（SSK－）MIMO over correlated rican fading channels：performance analysis and a new method for transmit－diversity ［J］.IEEE Transactions on Communications，2011，59 （1）：116－129.

［3］Tang Zijian，Cannizzaro R C，Leus G，et al.Pilot－assisted time－varing channel estimation for OFDM systems ［J］.IEEE Transactions on Signal Processing，2007，55 （5）：2226－2238.

［4］Pardes J L，Arge G R，Wang Zhongmin.Ultra－wideband compressing：channel estimation ［J］.IEEE Journal of Selected Topics in Signal Processing，2007，1 （3）：383－395.

［5］Berger C R，Wang Zhaohui，Huang Jianzhong，et al.Application of compressive sensing to sparse channel estimation ［J］.IEEE Communication Magazine，2010，48 （11）：164－174.

［6］Carboneli C，Vedantam S，Mitra U.Sparse channel estimation with zero tap detection ［J］.IEEE Transactions on Wireless Communications，2007，6 （5）：1743－1763.

［7］Mohimani H，Babaie－Zadeh M，Jutten C.Complex－valued sparse representation based on smooth L0 Norm ［C］／／Proceedings of ICASSP.Las Vegas：Conference Publications，2008：3881－3884.

［8］Candes E J.The restricted isometry property and its implications for compressed sensing ［J］.Comptes Rendus Mathmatique，2008，346 （9－10）：589－592.

［9］Wright J，Ganesh A，Yang A，et al.Robust face recognition via sparse representation ［J］.IEEE Transaction PAMI，2008，31 （2）：210－217.

［10］Waheed U Baiwa，Jarvis D Haupt，Gil M Raz，et al.Toeplitzstructured compressed sensing matrices ［C］／／IEEE／SSP 14th Workshop on Statistical Signal Processing，2007.

［11］Candes E，Romberg J，Tao T.Robust uncertainty principles：Exact signal reconstruction from highly incomplete frequency information ［J］.IEEE Transaction on Information Theory，2006，52 （2）：489－509.