基于引文网络的无标度网络模型探究

韩锦华

（陕西师范大学物理学与信息技术学院，陕西西安 710119）

信息交换网、社会网络、生物网络都是一些可用复杂网络描述的事例。传统研究复杂网络是用随机图来研究的。近年来，随着计算机能力的提高，使我们能够研究包含成千上万节点的复杂网络，与此同时，很多新概念、新测量方法如小世界网络、度分布、聚类系数等被提出来［1］。

随机图研究复杂网络的节点度分布是一个泊松分布。现在对复杂网络的研究结果是不同的：Redner研究了被科学信息研究所所收录的783339篇文章及在1975至1994年间发表在PRD上的24296篇文章的被引用次数的分布，发现它们服从指数为3的幂律分布，为无标度网络。事实上，很多实际复杂网络的节点度分布是幂律分布［1］。

研究无标度网络模型最早和最多的是BA无标度网络模型，但它不能用来解释现实中很多无标度网络的某些特性。比如上述事例中，并不是所有已发表过的文章都会被新发表的文章所引用，对于年代距今久远的文章，内容可能已经过时，不被引用，而年代距今很近的文章被引用的可能性较前者大一些。一篇文章被引用的概率将随着它已发表的时间的增长而降低，但根据BA无标度网络模型中的优先连接原则，一篇文章被引用的概率与它已发表的时间成正相关性，与实际情况相矛盾。再如，如果将BA无标度网络模型中最老的一些节点去掉，则它不再是无标度网络，但科学研究表明有些实际无标度网络如果去掉所有节点中最老的一部分，依然是无标度网络。为了解决这一矛盾，我们需要构建新的网络模型［2］。

1 模型A

我们将网络中节点比作被引用文章，而连线比作发表文章与被引文章的联系，节点的度表示文章被引的次数，从而构成引文网络。能够被引用的文章称为活跃节点，一篇文章直到不被引用时，则变为不活跃节点。当其不被引用时，则永远不被引用，即永远失活。如果一篇文章被引次数越多，则越不容易被遗忘，相反则越容易被遗忘。我们用ki表示节点的度，P表示节点失活的概率，则有P正比于1／（a+ki），其中a为偏置常数［2］。

设初始网络由m个活跃、完全连接的节点组成。

1.1 累积度分布

根据文献［2］［3］［4］，我们首先导出在某一时刻t时活跃节点的度分布p（k），对于k＞0，我们有

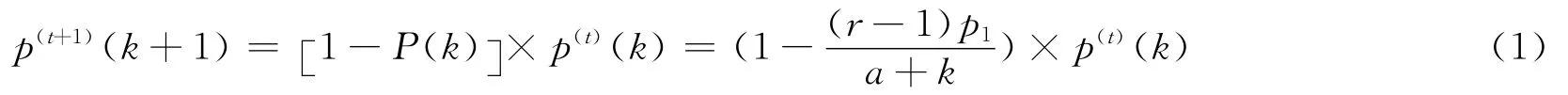
假设归一化因子r-1的浮动变化足够小，r可以看成是一个常数。静止情况下P（t+1）（k）＝P（t）（k）

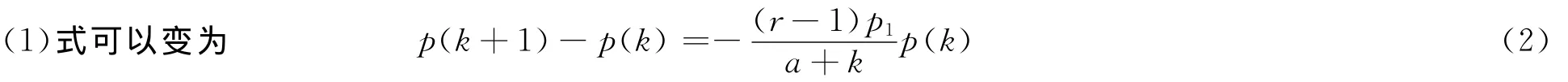
将k看成连续的，我们可将（2）写成

得到

b为归一化常数。整个网络中，相比所有点而言，m个活跃点数量是很小的，所以整个网络度分布N（k）可以近似只考虑失活点的度分布，我们有

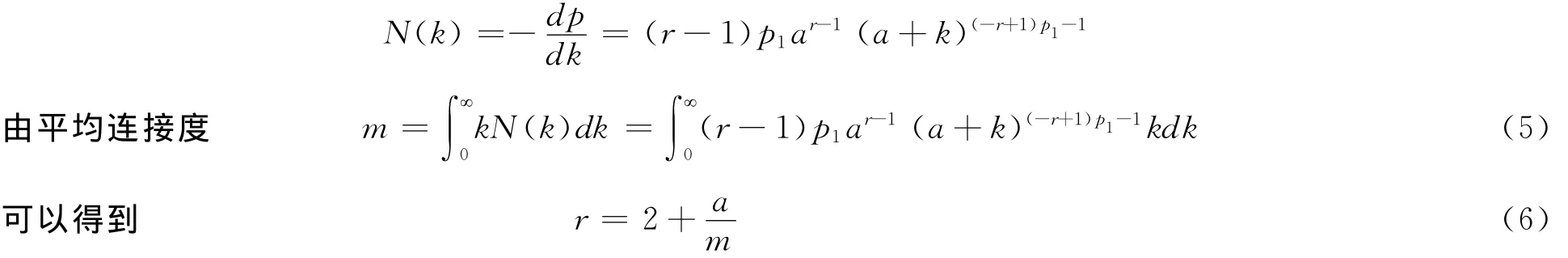
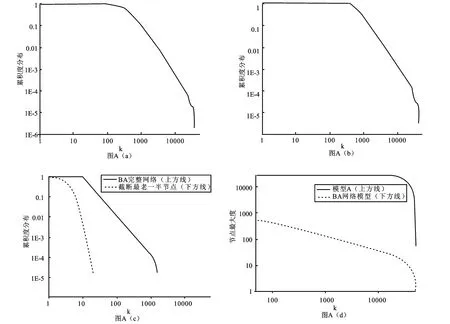
取m＝10，a＝10，p1＝0.99，运用Fortran90语言编程，模拟50000次时间步，独立重复10次，取平均得到累积度分布。如图A（a）所示，它是幂律分布，与很多实际复杂网络特征相符合。斜率为1.95即为指数，与方程（4）相似，略低于数值分析结果（r-1）p1＝1.98。其中横坐标表示网络节点的度，纵坐标表示大于对应其横坐标节点度的节点数占网络总节点数的比例。

上面我们考虑了包含网络中所有节点，但是在很多情况下，经验数据只包含网络中最近连接的新点及连线。比如在引文网络研究中所用文章距现在不能超过某一特定年份，这种网络称为截断网络。如图A（b）所示，其忽略了最老的一半节点及它们所有的连线。可以看到变化不大，与很多实际复杂网络特征相符合。而BA无标度网络中截断前与截断后的累积度分布变化比较大，与很多实际复杂网络特征不符。运用Fortran90语言编程，取初始节点数为10，模拟50000次时间步，独立重复10次，求平均后得到的BA无标度网络模型截断前及截断后累积度分布如图A（c）所示。

为了系统的观察截断带来的影响，我们考虑在不同截断节点数时网络节点的最大度。独立重复10次，取平均得到结果如图A（d）所示。其中横坐标表示截断其前一半节点及所有连线，纵坐标表示截断后此时网络中存在的节点中的节点最大度。

1.2 年龄分布

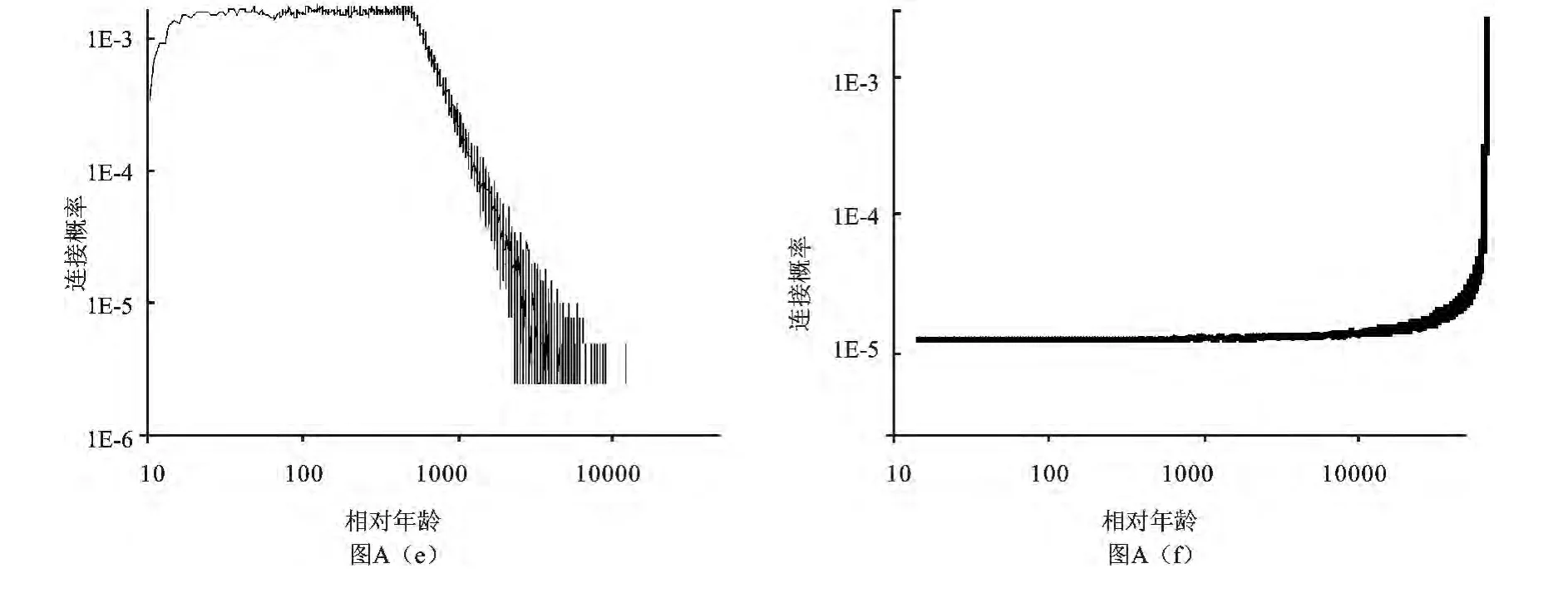
我们定义年龄分布h（τ）为在t时刻一条新边连接到年龄为τ的节点概率。因为只有活跃的节点才能够得到连线，对于这些节点，它们的年龄与它们的度有相同值，所以年龄为τ的节点获得一条新边的概率与这个节点有τ条边时能够活跃的概率相同（4）式，则h（τ）正比于（a+τ）-r+1。取上述相同的初始值及模拟方法得到结果如图A（e）所示。可以看到随着节点相对年龄的增大而连接概率有降低的趋势，与实际引文网络特征相符合。

而取初始网络节点数为10个点，模拟50000次时间步，独立重复10次，求平均得到的BA无标度网络结果如图A（f）所示，与实际引文网络特征不符合。

1.3 聚类系数

一般的，假设网络中的一个节点i有ki条边将它和其他节点相连，这ki个节点就称为节点i的邻居。显然在这ki个节点之间最多可能有ki（ki-1）／2条边，而这ki个节点之间实际存在的边数Ei和总的可能边数ki（ki-1）／2之比就定义为节点i的聚类系数Ci［5］14即：

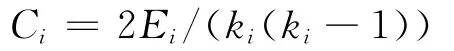
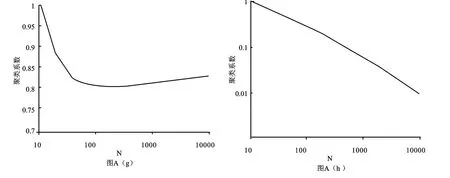
这里取与上述相同的初始值，模拟10000次时间步，独立重复10次，求平均得到结果如图A（g）所示。图中横坐标表示网络总共包含的节点数，纵坐标表示相应网络的聚类系数。而BA无标度网络模型中，随着网络包含节点数量的增加，其聚类系数迅速下降如图A（h）所示。

我们可以看到，随着网络包含节点数量的增加，其聚类系数趋向于0.82，此网络具有高聚类系数的特点，与实际网络如演员网络（C＝0.79）及科学合作网（C＝0.76）相似［1］。

2 模型B

只须将模型A第（2）步骤改为：将其随机与网络中已存在的活跃点中的m个活跃点相连接，每一个活跃节点只能被连接一次。模拟方法与模型A的方法完全相同。图B（a）为网络截断前与截断后的累积度分布，图B（b）为截断节点数与节点最大度关系图，图B（c）为节点相对年龄与连接概率关系图，图B（d）为网络大小与相应的聚类系数关系图。

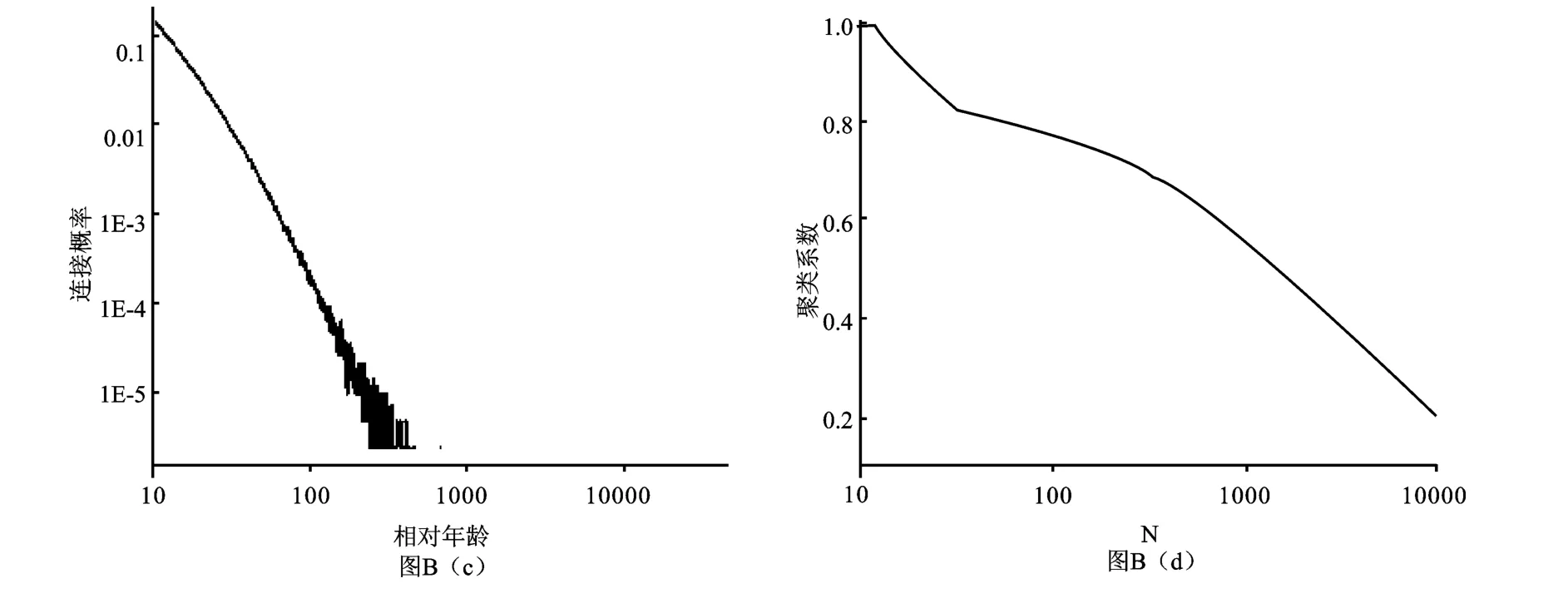
可以看到，图B（a），图B（b），图B（c）模拟结果与模型A相似，与实际引文网络特征相符合。图B（d）与电子邮件网（C＝0.16）［5］10相似。

3 延伸网络模型

只将模型A第（2）步骤改为以优先连接原则与m个活跃点连接，每一个活跃节点只能被连接一次，模拟结果与图A（c），图B（c）结果近似相同，而网络的大小与相应的聚类系数与上述模型有所不同。而只将模型A第（2）步骤改为将其与网络中已存在的活跃点中的最老（近）的m个活跃点相连接，模拟结果与模型A、B有很大差异。

综上所述，我们提出了两种基于节点失活的网络增长模型。通过数值计算分析和编程模拟，得到了网络节点截断前累积度幂律分布和随着截断节点数的增加而节点最大度下降关系。实际网络节点被截断后，累积度分布依然保持幂律分布的特征，随着节点年龄的增大而连接概率降低的特征，而这些特征用传统BA无标度网络模型无法解释。发现随着网络节点数的增大，其聚类系数保持比较大的数值，而BA无标度网络模型的特征恰恰相反。这些模型对于我们研究实际存在的复杂网络的拓扑性质及系统结构是有帮助的。

［1］ALBERT R，BARABA'SI A-L.Statistical mechanics of complex networks［J］.Rev.Mod.Phys，2002，74，47.

［2］KLEMM K，EGUILUZ V M.Highly clustered scale-free networks［J］.Phys.Rev.E，2002，65，036123.

［3］WU Zhi-xi，XU Xin-jian，WANG YING-Hai.Generating structured networks based on a weight-dependent deactivationmechanism［J］.Phys.Rev.E，2005，71，066124.

［4］TIAN Liang，ZHU Chen-ping，SHI Da-ning，GU Zhi-ming.Universal scaling behavior of clustering coefficient induced by deactivation mechanism［J］.Phys.Rev.E，2006，74，046103.

［5］汪小帆，等.复杂网络理论及其应用［M］.北京：清华大学出版社，2005.