有限体积法在二维稳态对流扩散方程中的稳定性分析
赵文娟,李春光,杨 程(1.宁夏大学土木与水利工程学院,宁夏银川750021;2.宁夏节水灌溉与水资源调控工程技术研究中心,宁夏银川750021;.北方民族大学土木工程学院,宁夏银川750021)
随着计算机技术的提升,近几年土壤水盐运移模型的研究工作已从一维逐渐过渡到多维。而求解这类模型的计算方法成为研究的重点。传统有限差分法中常规离散格式会对土壤水盐运移方程中的扩散项产生较大的影响,使得离散后方程组系数矩阵极易呈现病态,计算结果呈现出不稳定的伪振荡现象[1]。笔者利用有限体积法求解二维稳态对流扩散方程,通过数值模拟计算分析研究该数值方法的数学稳定性,为模拟计算土壤水盐运移过程提供前提条件。
1 有限体积法
有限体积法[2](Finite volume method)是将计算区域划分为一系列不重复的控制体积,并且使每个网格点周围有一个控制体积;将待解的微分方程对每一个控制体积积分,便得出一组离散方程。积分方程中每项都有明确的物理意义,从而使得方程离散时,对各离散项给出一定的物理解释。现就二维非饱和土壤水分运动方程为例,对其采用有限体积方法进行线性离散。
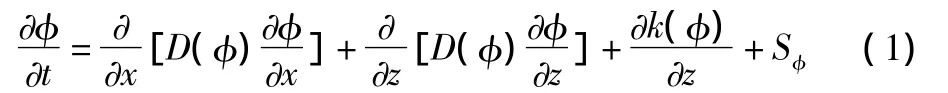
对式(1)在图1所示的控制体内积分,可得

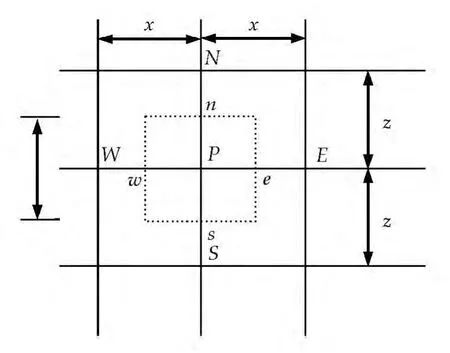
图1 网格节点控制体图
由于全隐式格式可以在较大时间步长保持计算结果的稳定性[3],采用全隐格式对扩散项进行时间上的积分,即
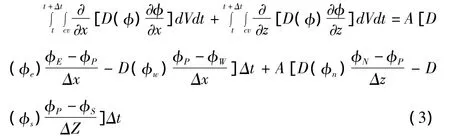
按节点场内的变量重新整理,可得

划分的网格节点构成的方程组再利用相应的迭代法进行计算求解。方程的数值解可通过增加迭代次数逼近到真实值。
有限体积法在计算偏微分方程中不仅可以得到较高精度的数值解,而且稳定性好。这些特点使其成为当前求解流动问题数值计算方法中最成功的方法[4]。1979年皇甫贵真[3]利用有限体积法求解Navier-Stokes方程组,解决了平板激波-附面层干扰和跨音速翼型黏性绕流问题。至今,有限体积法被分别应用到跨声速流场的数值计算[5-6]、地下水中污染质运移数值模拟[7]、河床变形数值模拟[8]以及结构动力学和结构可靠性等固体力学问题[9]中。
2 数值模拟
利用有限体积法分别模拟计算二维稳态对流扩散问题,验证该方法的数值解的稳定性。

选取网格节点数为8、20、50、100,将模拟计算得到的数值解与精确解进行对比。由图2可知,相对误差随网格节点数目的增加而降低,范围控制在1.2% ~6.9%。网格加密可以获得高精度的数值解。当网格节点较稀疏时,计算结果与精确值仍可以保持较高的吻合性。这说明有限体积法下大步长条件下是可以保障一定计算精度的。
2.2 算例2 已知二维稳态对流扩散方程为:
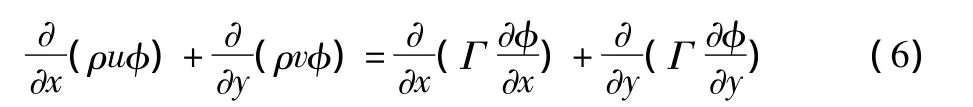
其中,ρu=5,ρv=2,Γ =1,Δx= Δy=0.2 m,计算区域东、南、西、北的边界值为固定值,分别为50、300、100和200。采用有限体积法对计算区域(图3)内的节点进行积分离散,最后得到二维稳态对流扩散方程计算节点的离散系数值和源汇项数值,迭代求解计算。

图2 不同网格数条件下的数值解与精确解对比
图3 计算区域图
模拟结果见图4。图a为9个计算节点模拟曲面图。8号节点温度在模拟计算后为最高值,2号节点的温度值为最小,与所给出的边界条件相吻合;当将网格节点加密,数目为25个时,模拟结果见图b,东侧接近边界的计算节点模拟曲线高出西侧的节点曲线值,计算断面呈现东高西底的断面形态。继续加密网格节点到49和100个(图c、d)。计算曲面随节点数目的增加逐渐稳定和光滑,且从计算结果呈现该区域温度在位置坐标(0.4,0.65)处为最低值为78,在位置坐标(0.8,0.56)处为节点最高值为300。在不同网格节点条件下,有限体积法模拟计算二维稳态对流扩散方程的数值收敛好。模拟结果验证了该数值方法是可用于实际工程方面的。
3 结论
采用有限体积法求解二维稳态对流扩散问题是可行的。通过算例验证,发现在加密网格条件下,数值解与精确解吻合度高且可较详实地呈现模拟形态;在稀疏网格条件下,数值解与精确值吻合较好且稳定性强,表明有限体积法具有良好的计算效果,可为模拟二维非饱和土壤水盐运移提供数学参考。
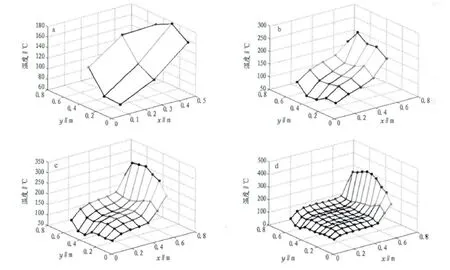
图4 不同网格数目条件下温度场模拟值
[1]钱凌志,冯新龙.对流占优扩散问题的特征AGE方法[J].计算数学学报,2011,33(4):347 -357.
[2]VERSTEEG H K,MALALASEKERA W.An introduction to Computational Fluid Dynamics:The Finite V Method[M].London:Longman Group Ltd,1995.
[3]姜启源,谢金星,叶俊.数学模型[M].北京:高等教育出版社,2011.
[4]李人宪.有限体积法基础[M].北京:国防科技出版社,2008.
[5]皇甫贵真.有限体积-时间分裂差分法及其对粘性流动的应用[J].航空计算技术,1979(1):75-115.
[6]周新海,朱方元,刘松龄.跨声速流场计算的时间分裂有限体积法[J].空气动力学学报,1981(3):82-91.
[7]PUTTI M,YEH W,MULDER W A.用三角形有限体积法高密迎风格式求解地下水运移方程[J].世界地质,1992(2):157-172.
[8]陆永军,张华庆.平面二维河床变形的数值模拟[J].水动力学研究与进展(A辑),1993(3):78 -79.
[9]陈浩.有限体积法在结构动力及可靠性分析中的应用[D].哈尔滨:哈尔滨工程大学,2012.

