轨面短波不平顺时域反演算法研究

毛晓君，周 宇，许玉德

（同济大学道路与交通工程教育部重点实验室，上海201804）

轨面短波不平顺是指钢轨顶面波长小于2 m的不平顺，主要包括轨面不均匀磨耗、轨面擦伤、剥离掉块、焊缝不平顺等，其波长小于1 m，幅值在1 mm 以内［1］。轨面短波不平顺对轮轨垂向力、钢轨振动加速度、轨道板振动加速度、底座板振动加速度和CA砂浆压应力均有显著的影响，且其影响程度超过中长波随机不平顺［2］。此外轨面短波不平顺会引起高频轮轨接触力［3］和冲击力［4-5］，加快钢轨、车轮及部件的伤损断裂［6］。国内外研究还发现，轮轨表面不平顺与轮轨滚动噪声直接相关，特别是在500～2 500 Hz频率范围内的噪声与轮轨表面短波不平顺幅值之间存在线性关系［7］。因此对轨面短波不平顺的分析，是合理进行钢轨养护维修、延长钢轨使用寿命、控制轮轨振动和噪声提高列车运行品质的重要基础。

而目前我国尚未对轨面短波不平顺展开较为系统的测量与分析，也未有典型的轨面短波不平顺频谱。单次测量得到的轨面短波不平顺时域波形又很难具备代表性。基于此，本文提出从轨面短波不平顺（粗糙度）水平谱反演短波不平顺时域波形的算法，并能保证一定代表性和随机性。结合上海地铁1号线实测得到的短波不平顺水平谱，反演得到了该线路时域内的短波不平顺波形。反演得到的短波不平顺时域波形可作为轮轨动力学仿真模型的激励输入，也可为预测轨面不平顺发展提供模拟数据。

1 轨面短波不平顺水平谱

由于轨面短波不平顺随线路里程变化表现为一定的空间随机性，因此往往将其转换到频域，再经1/3倍频程处理后通过轨面短波不平顺水平谱加以表现。

1.1 1/3倍频程

1/3倍频程是一种频域分析方法，它具有谱线少、带宽的特点，常用于声学、人体振动、机械振动等测试分析以及频带范围较宽的随机振动测试分析等［8］。1/3倍频程谱按逐级式频率进行分析，它是由多个带通滤波器并联组成，为的是使这些带通滤波器的带宽覆盖整个分析频带。根据国际电工委员会（IEC）的推荐，1/3倍频程的中心频率为

但在实际工程应用中，通常采用的中心频率是其近似值。此外，1/3倍频程的上、下限频率以及中心频率之间的关系为

式中：fm为上限频率；fl为下限频率；fc为中心频率。因此，1/3倍频程的带宽为Δf=fm-fl。

1.2 轨面短波不平顺度（粗糙度）水平

轨面粗糙度水平是指经1/3倍频带通滤波后，对每一带宽内的波形计算其均方根r~k（root mean square，RMS），并除以参考值rref后，换算到水平级，从而对轨面短波不平顺进行衡量。对于一段测量长度为L的轨面不平顺，经1/3 倍频带通滤波后在某一带宽k内的均方根计算如图1和公式（3）所示

式中：Yi是带宽k内的信号采样值，n为长度L内的采样点数。

图1 轨面短波不平顺均方值计算示意图Fig.1 Mean square value calculation diagram of rail surface shortwave irregularities

图1中，x为线路里程长度；L为线路长度。

一定长度范围内短波不平顺幅值的均方根直观地反映了该段轨面不平顺在特定带宽内的粗糙程度。在得到各带宽内的均方根后，通过公式（4）计算便可得到各带宽内对应的短波不平顺粗糙度水平［9］。

目前只有欧洲铁路在研究轮轨噪声时制订了轨面的不平顺度（粗糙度）水平——ISO3095标准［9］对轨面不平顺度进行评价，它是从轨道车辆车外辐射噪声的角度对钢轨表面轮轨粗糙度进行评价控制，此外标准中还制定了相应的噪声测量方法。之后欧洲铁研究所（ERRI）采用德国Müller-BBM公司开发的mbbm-RM1200轨面不平顺度测量仪对欧洲铁路的轨面进行了不平顺度测量，统计得到了ISO3095轨面粗糙度水平标准限值。

2 轨面短波不平顺时域波形反演算法

2.1 反演算法的基本思想

轨面短波不平顺时域波形反演算法的思想是从短波不平顺粗糙度水平谱出发，按照1/3倍频程的带宽划分，将1 m以下的短波不平顺分成若干个频带（波长带）。在每个波长带中生成若干不同波长、相位且振幅为1的正弦波，再通过振幅的调整，使得该波长带中的若干正弦波叠加后经计算得到的粗糙度水平与标准或实测结果的相同。具体算法流程可分为以下6个步骤。

1）将1 m以下的短波按照1/3倍频程的中心波长划分成24个频带，各频带中心波长、上下截止波长见表1。

2）在每一个波长里，将波长等步长细分成m份，其中最小波长为该频带的下截止波长，最大波长为该频带的上截止波长。

3）根据上述波长，在第i个频带内产生m个振幅为1，相位在［0，2π］间随机分布的正弦波，并叠加得到一个复合波。式中：x为线路里程的离散形式；λij为第i个频带内第j个谐波的长度；φij为第i个频带内第j个谐波的相位。

4）对上述复合波按式（3）进行均方根计算，得到均方根ri。

5）根据式（5）计算每个频带内的振幅ai

式中：Li是在第i个频带内的粗糙度水平，由（4）式计算得到，可以是若干实测数据的计算平均，也可以是ISO3095的标准值；rref为参考值，同样取rref=1 μm。

6）将各频带不同波长的波按照式（6）复合叠加，由此构成［4.5，1 140.4］mm波长范围内任意长度轨面短波不平顺的时域模拟值。

表1 1/3倍频程中心波长、上下截止波长Tab.1 Central and cut-off wavelength of 1/3 octave mm

2.2 ISO3095标准谱反演

按照上述构造思想，在钢轨粗糙度水平ISO3095标准的基础上，对其进行反演，得到时域波形如图2所示。

图2中，模拟线路长度为10 m，模拟得到的短波不平顺时域波形幅值在±0.1 mm之间，符合实际情况。此外，构造算法中由于各正弦波的相位是随机产生的，因此基于同一个粗糙度水平谱，可得到无数多个短波不平顺时域模拟波形，这在保证代表性的同时又保证了随机性。

对上述反演得到的短波不平顺进行粗糙度水平计算，结果与ISO3095标准限值对比，如图3所示。

从图3中可以看出，由反演得到的时域波形计算得到的粗糙度水平谱与ISO3095标准谱吻合得很好，验证了上述算法的可行性与正确性。因此，该反演算法可进一步用于实测钢轨表面粗糙度水平谱的轨面短波不平顺波形反演。

图2 ISO3095标准反演得到的短波不平顺波形Fig.2 Rail surface shortwave irregularities inverted from ISO3095 standard

图3 ISO3095标准谱与反演谱对比Fig.3 Contrast between ISO3095 standard spectrum and inverse spectrum

3 实测水平谱反演

3.1 测试仪器及数据来源

轨面短波不平顺的测量采用RMF-2.3E型波磨测量仪，该测量小车可以实现钢轨表面纵向波浪形磨耗的在线连续测量，其技术参数见表2所示。

表2 RMF-2.3E型波磨测量仪测量参数Tab.2 Parameters of RMF-2.3E corrugation detection instrument

用RMF-2.3E 型波磨测量仪对上海轨道交通1 号线隧道地段一段450 m 长的轨面短波不平顺进行测量，测量结果经［4.5，1140.4］mm带通滤波后得到时域波形如图4所示。

3.2 实测水平谱反演与对比

对上述实测轨面短波不平顺数据做1/3倍频程处理并换算成分贝做轨面粗糙度水平谱，得到各中心波长处的粗糙度水平Li。利用反演算法进行时域内轨面短波不平顺的反演，反演长度与原始数据长度一致，反演得到的时域波形如图5所示。

对比图4、图5 可知，反演得到的时域波形幅值主要集中于-0.2～0.2 mm 间，而实测波形有更大的离散性，存在较多异常值。造成这一差异的原因在于，反演得到的波形是由若干不同振幅、波长和相位的正弦波叠加而成的，这一过程将轨面短波不平顺视为平稳的高斯过程，而实际轨面短波不平顺的形成和发展是很多随机性因素共同作用的结果，因而并不是严格平稳随机过程，所以反演得到的时域波形与原始实测波形存在一定偏差。

图4 ［4.5，1 140.4］mm滤波后的实测轨面短波不平顺波形Fig.4 Measured rail surface shortwave irregularities after［4.5，1 140.4］mm band pass filtering

但尽管如此，上述反演算法的优点在于，能够保证反演波形的轨面粗糙度水平谱与实测数据粗糙度基本吻合，如图6所示。

图5 实测数据反演得到的轨面短波不平顺波形Fig.5 Inverted rail surface shortwave irregularities based on measured datum

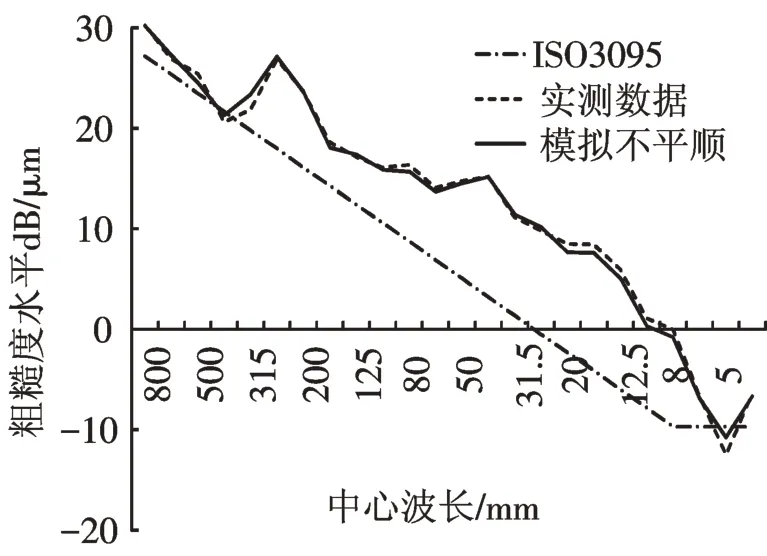
图6 实测轨面短波不平顺粗糙度谱与反演谱对比Fig.6 Contrast between measured spectrum and inverse spectrum

因此，反演算法得到的时域波形在频域内与原始数据一致，即能保证在短波范围内具有相同的波长组成，这是该反演算法的最主要目的和意义。

4 结论

轨面短波不平顺对高频轮轨接触力、冲击力、轨道各部件振动加速度、轮轨噪声等方面都有显著的影响，而目前国内外尚未有典型的轨面短波不平顺频谱，且单次测量结果又很难具备代表性。基于此，本文创造性地提出一种从轨面短波不平顺（粗糙度）水平谱反演短波不平顺时域波形的算法，并用该算法实现了ISO3095标准谱与上海轨道交通实测谱的反演，得到以下结论：

1）反演得到的时域波形计算得到的粗糙度水平谱能与ISO3095标准谱和实测谱较好吻合，验证了算法的可行性和正确性；

2）反演算法中由于各正弦波的相位是随机产生的，因此基于同一个粗糙度水平谱，可反演得到无数多个短波不平顺时域模拟波形，这使得反演算法在保证代表性的同时又具备了一定随机性；

3）反演过程将轨面短波不平顺视为平稳的高斯过程，而实际轨面短波不平顺并不满足严格平稳性，因此反演波形与原始实测波形存在一定偏差。反演波形更平稳，对于实测波形的大离散性和异常值不能模拟。

4）轨面短波不平顺时域波形反演算法的提出为进一步研究振动噪声和轨面状态仿真分析提供了数学方法。

［1］罗林，张格明，吴旺青，等.轮轨系统轨道平顺状态的控制［M］.北京：中国铁道出版社，2006：7-9.

［2］徐庆元，曹扬风，周小林，等.短波随机不平顺对列车-板式无砟轨道-路基系统振动特性的影响［J］.中南大学学报：自然科学版，2011，42（4）：1105-1110.

［3］NIELSEN JCO. Rail roughness level assessment based on high-frequency wheel-rail contact force measurements［J］. Noise and Vibration Mitigation，2008，99：355-362.

［4］韦红亮，练松良，周宇，轨面不平顺对高架支承块轨道结构振动特性影响试验研究［J］.中国铁道科学，2011，32（6）：22-27.

［5］陈敏敏，练松良，程小平，等.接头区轨面短波不平顺与P1、P2力关系的试验研究［J］.兰州交通大学学报，2011，30（1）：59-63.

［6］瞿锋.城市轨道交通曲线钢轨短波不平顺分析［J］.城市轨道交通研究，2011，14（8）：65-68.

［7］THOMSON D J. On the relationship between wheel and rail surface roughness and rolling noise［J］. Journal of Sound and Vibration，1996，193（1）：149-160.

［8］王济，胡晓.MATLAB在振动信号处理中的应用［M］.北京：中国水利水电出版社，2006.

［9］EN ISO3095.Railway application-acoustics-measurement of noise emitted by rail bound vehicles［S］.Switzerland，2005.