波动输入方法及其在水闸工程中的应用

杨启龙，白莉萍，耿 亮

（1.河海大学水利水电学院，江苏南京210098；2.徐州市水利建筑设计研究院，江苏徐州221002）

水闸作为典型的挡水建筑物，在水利工程建设中有着广泛应用，而对于地处地震烈度较大的地区的闸涵结构，抗震计算十分重要。相对于传统地震动分析中的无质量地基模型，如何有效模拟无限地基辐射阻尼效应并合理确定地震动输入方法是结构-地基相互作用分析中需要考虑的重要问题。在有限元动力分析时，由于计算条件的限制，一般会从无限域地基中截取有限计算区域，为使外传散射波在达到截断边界时不产生反射，需要通过在截断处设置人工边界以模拟无限地基辐射阻尼。目前适用性较广的人工边界有黏性边界［1］、黏弹性边界［2］、叠加边界［3］、人工透射边界等［4］。黏性边界由于无法考虑介质的弹性恢复力，容易出现低频失稳的现象；透射边界在实际应用时存在着高频振荡问题；黏弹性边界是在黏性边界的基础上在人工边界上设置弹簧单元来模拟远域地基的弹性恢复能力，其因为拥有较好的高、低频段稳定性且较容易施加而被广为应用。采用黏弹性边界模拟地基辐射阻尼并进行动力分析时，往往通过在边界节点上施加相应等效节点荷载进而完成相应地震动的输入。鉴此，本文基于有限元软件ADINA，在研究了粘弹性边界的基础上，将波动输入方法应用于某软基上水闸闸室—水体—地基系统的地震动反应分析中。结果表明，本文方法有较好的精度与稳定性，适用于水闸等软土地基工程的地震动分析，计算方法与结果可为相关工程提供参考。

1 理论及方法

1.1 闸室-水体耦合模型

对于闸室结构内的U形水域，闸室-水体间的相互作用问题可以采用流固耦合的方式进行求解。ADINA软件提供了基于水体无漩、无黏、边界小位移的势流体模型，结构-水体系统的流固耦合方程为［5］

式中：MSS，KSS，CSS，FSS分别为结构的质量矩阵、刚度矩阵、阻尼矩阵和荷载矢量；MFF为流体质量矩阵；CUU，CUF，CFU，CFF分别为流体与固体交界面上固体本身的、流体对固体作用的、固体对流体作用的、流体本身的阻尼矩阵；KUU，KUF，KFU，KFF分别为流体与固体交界面上固体本身的、流体对固体作用的、固体对流体作用的、流体本身的刚度矩阵；FU为外力矢量变量，FF，(FF)S分别为结构边界上所受到的流体的压力、流体连续性方程所对应的体积积分项与面积积分项。

1.2 黏弹性边界单元与波动输入方法

黏弹性人工边界是指在计算模型的截断边界上设置连续分布的并联弹簧-阻尼元件［6］，弹簧阻尼元件相关参数计算公式为

式中：KN为边界元件的法向刚度；KT为边界元件的切向刚度；CN为边界元件的法向阻尼系数；CT为边界元件的切向阻尼系数；ρ为介质的密度；G为介质的剪切模量；cp为介质P波波速；cs为介质S波波速；R为散射波波源与边界之间的距离；αN为边界元件的法向修正系数；αT为边界元件的切向修正系数。

根据力学平衡性方程和位移连续性方程，模型的人工边界上任意一节点n的运动可用如下方程表示

式中：Kn为节点n处附加的弹簧刚度，Cn为节点n处附加的阻尼系数；(t)为为了模拟边界自由场进而在n点施加的等效节点荷载，(t)为为了模拟边界散射场进而在n点施加的等效节点荷载。

通过将输入的地震波转化为黏弹性人工边界上的等效节点荷载，即可实现波动在边界上的输入。在模拟边界自由场时荷载在边界的施加包括两个部分，一部分为自由场在人工边界处的应力场，另外一部分为为了克服人工边界单元阻尼和刚度需要的力。节点等效荷载的公式如下所示：

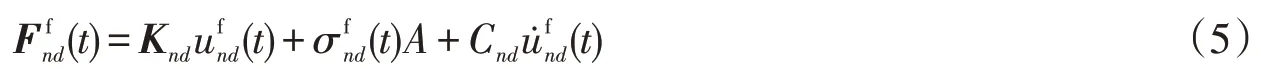
2 算例验证

为了验证三维黏弹性人工边界与波动输入方法的可行性和精度，下面开始分析均质三维半空间域内的波动问题。如图1为空间半无限地基上所截取的一块分析域，模型X向长度为400 m，Y向长度为400 m，Z向长度为600 m。介质剪切模量为2 GPa，泊松比为0.22，密度为2 000 kg·m-3，模型单元网格长度为20 m。荷载施加步数共600步，荷载总时长为6秒，荷载为从模型底边界垂直入射P波和S波，其中P波波速为1 000 m·s-1，S波波速为1 669 m·s-1，位移荷载公式如下所示：

模型四周及底部边界通过布置弹簧阻尼元件处理为黏弹性人工边界，计算时本文取人工边界修正系数αN=1.33，αT=0.67，散射波源至侧边界长度本文取200 m，散射波源至底边界长度取600 m，人工边界上的弹簧阻尼元件相关参数利用式（2）、式（3）计算即可以得到。模型位移观测点取模型底部中心点A点和模型顶部中心点B点。

图2为观测点A，B的位移时程曲线，从图中可以看出，由模型底部入射的P波和S波到达模型自由面时位移波形均有一倍放大，而由自由面反射回来的波形在达到截断边界后被黏弹性人工边界吸收，该算例验证了人工边界设置与波动输入方法的正确性与精度。

图1 波动输入有限元模型Fig.1 Schematic diagram of wave input model

图2 观测点A、B位移时程曲线Fig.2 Time-history curve of displacement of point A and B

3 工程实例

3.1 工程简介

采用上述方法对江苏省某水闸闸室结构进行动力分析。该水闸地处软土地基上，闸址位于抗震不利地段，按规范要求需进行抗震计算［8］。闸室顺水流向长13.00 m，垂直水流向长35.80 m，闸室高13.60 m，闸室内水深4.9 m。地基范围向四周取一倍结构高度尺寸，考虑正常通航工况。为模拟流固耦合效应划分了水体网格，水体网格单元采用势流体单元进行模拟，整体三维有限元模型见图3。由于水闸的闸墩在垂直于水流方向的刚度较小，在地震作用中容易引起震损，因此本文计算中主要考虑对结构影响最大的横河向地震。为了对比使用本文波动输入方法的效果，分别采用无质量地基模型和黏弹性边界模型进行动力计算，计算方法为时域分析方法。采用无质量地基模型进行模拟时，四周边界法向链杆约束，底部固定约束，地震荷载以加速度的形式施加在闸室结构上；采用黏弹性边界模型进行模拟时，截断边界与固定的弹簧阻尼元件相连，通过施加边界节点荷载完成地震动的输入。计算时间步长0.01 s，共1 000步，历时10 s。系统阻尼比取5%。水体体积模量为2 200 MPa，密度为1 000 kg·m-3，结构和土体参数见表1（结构动弹模较静态标准提高30%）：

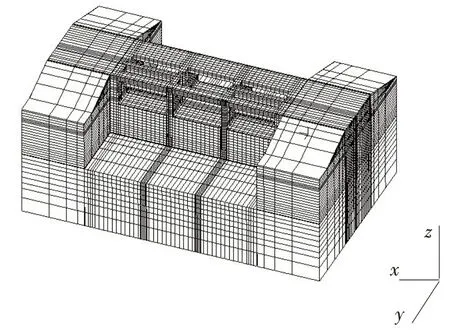
图3 整体结构有限元模型Fig.3 Finite element model of whole structure

图4 闸墩及关键点Fig.4 Gate pier and the key points

设计地震时地基水平向峰值加速度为0.2 g，场地为Ⅲ类场地，相应特征周期0.35 s。输入的地震动加速度时程曲线如图5 所示。本文通过将静力计算结果与纯动力计算结果叠加进而完成动力分析。

表1 材料参数Tab.1 Material parameters

图5 输入地震波的加速度时程曲线Fig.5 Time-history curve of acceleration of seismic wave

3.2 成果分析

成果分析对象为动静叠加的计算结果，叠加时结构关键部位动应力依照规范进行折减，折减系数取0.35［9］。考虑到水闸横河向的对称性分布，对闸墩关键点分析时取右岸侧中墩和边墩进行考虑，见图4。分别用无质量地基和黏弹性边界模型对结构进行计算，得到闸墩顶底关键点G点与A点之间的横河向相对位移时程曲线见图6，闸墩底部应力关键点E点竖向应力时程图见图7。由图6、图7可以看出，采用黏弹性边界模型计算得到的结构顶底相对位移和应力关键点竖向应力普遍小于通过无质量地基模型计算得到的结构顶底相对位移和应力关键点竖向应力相应的计算数值。表2和表3分别为两种不同计算方法下闸墩顶底关键点相对位移最大值和底部应力关键点竖向应力最大值。由表中可以看出，采用黏弹性边界模型计算得到的结构顶底关键点相对位移峰值比采用无质量地基模型计算得到的结构顶底相对位移峰值减小约35%，采用黏弹性边界模型计算得到的结构底部关键点竖向应力峰值比采用无质量地基模型计算得到的结构底部关键点竖向应力峰值亦有相应程度减小。采用黏弹性边界模型可以有效考虑地基辐射阻尼效应，地震动响应下的闸墩顶底相对位移和控制点拉应力均有一定幅度减小。

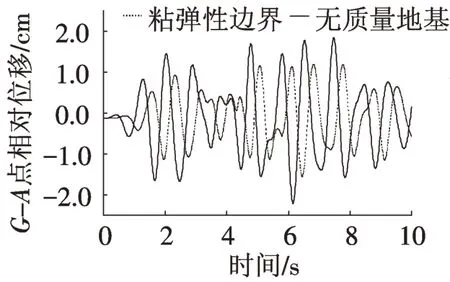
图6 关键点G与A横河向相对位移时程曲线Fig.6 Time-history curve of vertical relative displacement between key points A and G

图7 关键点E竖向应力时程曲线Fig.7 Time-history curve of vertical stress of key point E

表2 闸墩关键点横河向相对位移峰值Tab.2 The peak relative displacement between key points

表3 闸墩底部关键点竖向应力峰值Tab.3 The peak vertical stress of key points of gate pier

4 结语

本文基于有限元计算软件ADINA，在考虑地基辐射阻尼的情况下，编制了相关公式计算程序，成功实现了外源波动在边界上的输入，并将该方法应用到软土地基上水闸结构动力计算当中。计算结果表明，考虑地基辐射阻尼效应下水闸结构的地震动反应较传统无质量地基方法有所减小，从充分利用结构材料强度的角度讲，地基辐射阻尼效应在实际工程设计建造过程中应予以适当考量。针对软基上结构动力计算该方法具有良好的精度和稳定性，足以满足工程要求，是一种有效的分析计算方法，本文的计算方法与结论可为相关工程分析与设计提供参考。

［1］LYSMER J，KULEMEYER R L.Finite dynamic model for infinite media［J］.Journal of the Engineering Mechanics，ASCE，1969，95（4）：859-878.

［2］DEEKS A J，RANDOLPH M F.Axisymmetric time-domain transmitting boundaries［J］. Journal of Engineering Mechanics，1994，120（1）：25-42.

［3］SMITH W D.A non-reflecting plane boundary for wave propagation problems［J］.Journal of Computational Physics，1973，15：492-503.

［4］廖振鹏.工程波动理论导论［M］.2版.北京：科学出版社，2002：168-173.

［5］龚存燕.基于ADINA流固耦合方法的高耸进水塔地震反应分析［D］.南京：河海大学，2010：21-23.

［6］刘云贺，张伯艳，陈厚群.拱坝地震动输入模型中黏弹性边界与黏性边界的比较［J］.水利学报，2006，37（6）：758-763.

［7］杜修力，赵密.基于黏弹性边界的拱坝地震反应分析方法［J］.水利学报，2006，37（9）：1063-1069.

［8］卢华喜.不同频谱特性地震动输入下的场地地震反应［J］.华东交通大学学报，2007，24（1）：22-25.

［9］中国水利水电科学院研究院.SL203-97水工建筑物抗震设计规范［S］.北京：中国水利水电出版社，1997.