卫星推进分系统发动机螺接头漏率变化规律试验研究

李晓丽，王 勇，刘 胜，周雪茜，王 凯

（北京卫星环境工程研究所，北京 100094）

0 引言

卫星推进系统的发动机管路连接常采用球头-锥面螺接密封结构形式（以下简称螺接头），其密封性能直接关系到卫星发射的成败及飞行寿命，因此在发动机螺接头装配后，必须进行密封性能检测。 针对发动机螺接头，采取向发动机管路系统充压的方法进行检漏。充压后进行多次复测发现，漏率值不尽相同。因此，有必要研究螺接头漏率变化规律，为实际工程应用提供依据。截至目前，国内外尚未有螺接头漏率变化规律试验研究的相关报道。 本试验的出发点是以螺接头初始漏率接近合格范围为标准，目的是摸索变化规律，避免因误判而带来的返工或等待时间，提高检漏工作效率和准确性。

1 球头-锥面密封结构的泄漏机理

球头-锥面密封结构是国内卫星推进系统广泛采用的一种静密封形式（图1）。球头和锥面在拧紧之前为线接触，当施加拧紧力矩后，球头和锥面发生弹塑性变形，使球头和锥面之间形成一个环状密封面。

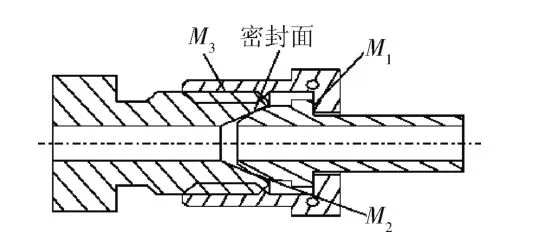
图1 球头-锥面连接密封结构示意图Fig.1 The orbicular sealing joint

球头与锥面拧紧过程中，需要克服3个接触表面的摩擦力矩，即外套螺母和球头支撑面间的摩擦力矩M1，球头和锥面间的摩擦力矩M2以及内外螺纹间的摩擦力矩M3：

因此，拧紧力矩为

式中：Ff为轴向预紧力；dw为支撑面等效直径；µw为支撑面摩擦因数；d2为球头-锥面接触面的等效直径；µ2为球头-锥面接触面摩擦系数；α为锥面倾角；dp为外螺纹有效直径；µs为螺纹副摩擦因数；β为螺纹升角。

操作过程中，操作者施加的拧紧力矩转化为夹紧球面和锥面的预紧力。在预紧力的作用下，球头表面和锥表面形成接触面[1-2]。球头材料TC4 屈服强度较大，而锥面材料1Cr18Ni9Ti 屈服强度较小，易发生塑性变形[3-5]。在球头及锥面上都存在凹凸不平的微小“峰”和“谷”，随着2 个接触面正向的相互挤压和切向的相互错动，“峰”被逐渐削平，“谷”被逐渐填满。图2为假设理想状态下球头及锥面压紧前后的截面结构。

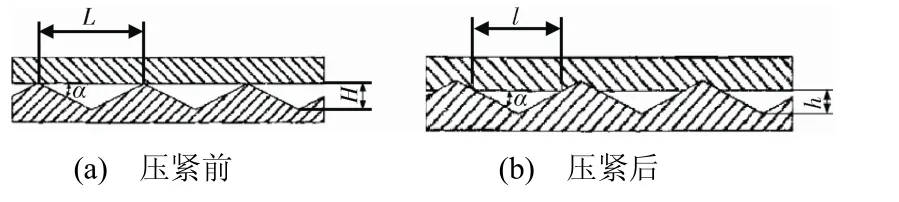
图2 理想状态下两个密封面压紧前后截面形式Fig.2 The section of the leak path on the sealing surface

受加工和装配质量等多种因素的综合影响，实际球头、锥面的“峰”和“谷”不可能呈规律分布，连接后肯定存在一些缝隙，这些缝隙会成为泄漏的“通道”。球头-锥面压紧前后的结构如图3所示。

图3 球头-锥面材料压紧前后结构示意图Fig.3 The structure of sphere-cone joint before and after compacting

2 试验原理及方法

2.1 试验原理

选择刚装配好的发动机螺接头进行漏率检测试验，以研究泄漏随时间的变化规律。本试验中，漏率稳定的判据是：连续6 h 以上保持不变。

发动机螺接头漏率检测试验原理如图4所示，由试验平台、充排气控制台、检漏设备、计算机和计算机实时显示器组成。

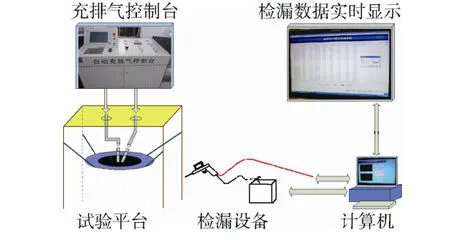
图4 螺接头漏率变化规律试验原理图Fig.4 The method of orbicular sealing joint leak detection

首先，根据模拟边界条件搭建试验平台；然后由充排气控制台对试验平台中的发动机管路充压；最后利用检漏设备对漏率（Qx）进行检测，并实时显示。在一段时间内通过对试验件的连续检测，可获得一系列的数据；通过对多组试验件的检测可得到多组样本漏率-时间变化关系曲线图。

2.2 试验方法

螺接头漏率检测采用氦质谱吸枪法[6-8]（如图5所示），首先用专用包覆胶布将螺接头区域包覆，使形成一个密闭的收集空间，然后往待检系统充入规定压力的高纯氦气。氦质谱检漏仪通过软管与吸枪相连，以收集由螺接头“通道”泄漏的氦气。

图5 氦质谱吸枪法示意图Fig.5 Schematic diagram of the sniffing probe leak detector

吸枪探测得到螺接头的漏率测试值Qx，通过正压漏孔标定设备得到螺接头的漏率真实值Q：

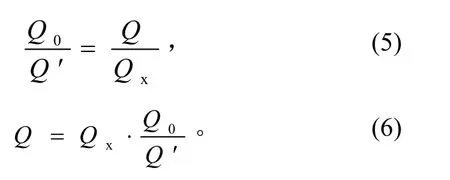
其中：Q0为校准漏孔的标称漏率；Q′为校准漏孔的检测漏率。

3 试验装置

漏率检测的试验平台由卫星结构件、发动机管路、发动机模拟件及发动机支架等组成，发动机管路的末端焊接球头，发动机模拟件由法兰及电磁阀体组成如图6、图7所示。

图6 漏率试验平台Fig.6 Leakage test platform

图7 发动机模拟件与管路连接图Fig.7 Globe-cone joint

试验开始前，将发动机模拟件固定在发动机支架上，然后将发动机末端的球头与模拟件上的电磁阀体内锥面以螺接方式连接，实物如图7所示。每完成一轮试验，拆下电磁阀体和法兰连接的螺钉更换新电磁阀体，切割球头管路并进行新球头管路的焊接，开展多轮重复性试验。

本试验研究有6 组试验件，每组试验件均进行6 次装配，摸索在给定压力条件下，螺接头漏率随时间的变化规律，这6 组试验件均包含2 个支路，分别标记为A 支路（图7中的垂直管路）和B 支路（图7中的倾斜管路）。试验可得到共计72 个数据样本。该6 组试验件与实际卫星螺接头加工及连接方式完全一致。6 次装配分别为：球头-电磁阀锥面第1 次装配，第2 次装配，第3 次装配，以及加垫圈后第1 次装配，第2 次装配和第3 次装配。通过以上6 种装配过程，验证球头-锥面反复装配及加垫后多次装配对漏率的影响。在装配之前均需进行管路泄压，将上一次装配的球头完全拧松，再完成新一轮的对中拧紧操作。每完成1 组试验件的6 次装配及检漏过程，即可进行下一组试验件的装配及检漏试验。具体流程如图8所示。

图8 发动机螺接头漏率试验流程Fig.8 Flow chart of sphere-cone joint leak testing for engines

4 试验过程及结果分析

4.1 确定漏率敏感区

假设球头及锥表面材料完全光滑，球头-锥面 拧紧贴合后不存在材料的磨损，且连接为完全“对中”状态，那么，从球头与锥面刚刚接触到逐渐施加拧紧力矩开始检测，螺接头的漏率随拧紧力矩的增加，先减小然后趋于稳定，最终漏率小于1×10-8Pa·m3/s（达到氦质谱吸枪法的检漏灵敏度）。漏率稳定之前的区域，称之为漏率敏感区，如图9所示。

图9 漏率随拧紧力矩变化示意Fig.9 Schematic diagram of relationship between leakage rate and moment

一般情况下，卫星发动机螺接头的漏率指标要求优于1×10-6Pa·m3/s。本研究中，为保证模拟发动机管路系统加压后，球头有持续的泄漏，漏率100%可检测：首先需进行初始拧紧力矩的摸索，从而确定漏率敏感区。A 支路、B 支路在20 N·m 的初始力矩下的漏率值如表1所示。

表1 两个支路在20 N·m 的初始力矩下的漏率Table 1 Leakage rate of two sub-pipelines under a moment of 20 N·m

由表1可知，在20 N·m 的初始力矩下，A 支路螺接头漏率先增加，经过约40 min 后漏率趋于稳定，并稳定在7.0×10-7Pa·m3/s 左右；B 支路螺接头漏率约50 min 后趋于稳定，维持在4.0×10-6Pa·m3/s 左右。为满足工程应用的需要，最终确定的力矩值除了应确保螺接头有持续的漏率外，初始漏率值还应尽可能小于1.0×10-6Pa·m3/s。A 支路初始力矩为20 N·m可以满足上述要求，因此20 N·m 作为A 支路拧紧力矩；将B 支路的初始力矩在20 N·m 的基础上增加5 N·m，即观察其漏率随时间的变化。B 支路螺接头在25 N·m 初始力矩下的漏率如表2所示。由表2可知，B 支路在25 N·m 的初始力矩下可满足螺接头有持续漏率且漏率小于1.0×10-6Pa·m3/s 的条件。并且经过约70 min 后，漏率趋于稳定。

表2 B 支路在25 N·m 的初始力矩下的漏率值Table 2 Leakage rate of the sub-pipeline B under a moment of 25 N·m

本研究中，以上述基准力矩（A 支路20 N·m；B 支路25 N·m）为参考，结合实际情况上下微调拧紧力矩，进行螺接头的装配。

4.2 两个支路的螺接头漏率变化试验结果

6 组试验件（均包含A 支路、B 支路螺接头）在完成6 次装配并充压检漏后，共得到72 个漏率-时间样本，几种典型的漏率变化曲线如图10所示。

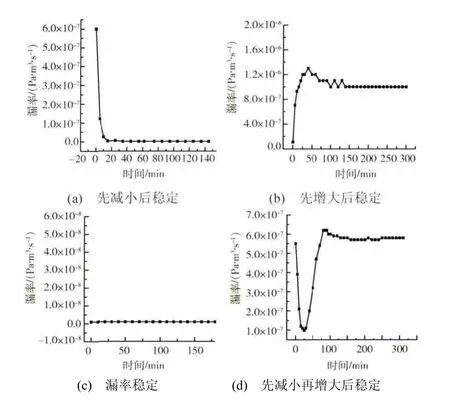
图10 典型漏率-时间变化关系曲线Fig.10 Representative curves of leakage rate vs.time

通过72 个样本结果，可得出漏率变化趋势统计结果，如图11所示。

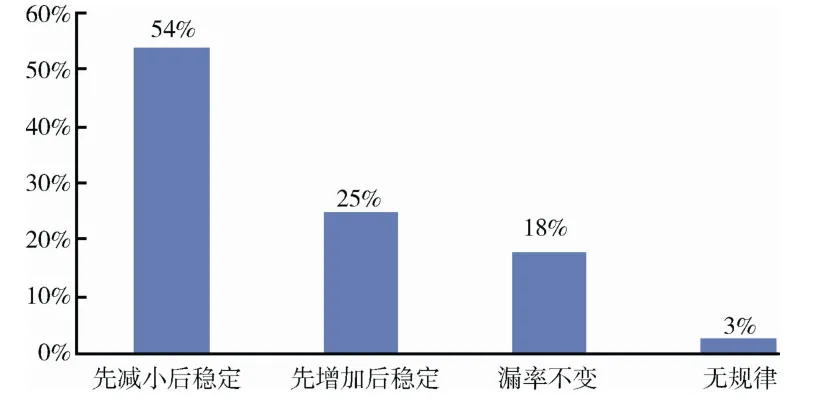
图11 漏率变化趋势统计Fig.11 Statistics of the leakage rate variation

对漏率变化的统计分析可知，加垫前后3 次装配过程对漏率变化的影响不明显。在确保螺接头有持续泄漏的前提下，将力矩值固定，仅研究螺接头漏率随时间的变化，有以下4 种趋势：

1）漏率随时间的增加单调减小，最终趋于稳定，该情况占54%；

2）漏率随时间的增加单调增大，最终趋于稳定，该情况占25%；

3）漏率随时间的增加始终稳定，漏率值一般为1.0×10-8Pa·m3/s，该情况占18%；

4）漏率随时间的增加先减小（或增大），再增大（或减小），但最终趋于稳定，该情况占3%。

4.3 影响因素分析

螺接头的漏率随时间的增加而表现出比较复杂的变化关系。针对同一组螺接头，漏率变化规律也不尽相同，这是因为螺接头的密封面的质量有差异[9-12]。影响密封面质量的因素按照影响性质可以分为零部件加工因素和装配操作因素，进行故障树分析如图12所示。

图12 密封性主要影响因素的故障树分析Fig.12 Fault tree of main affecting factors for sphere-cone joint leakage rate

零部件加工因素是指粗糙度、零件配合面外形与理论形面的偏差等；装配操作因素包括操作经验、操作方法等，体现在对球头与电磁阀体的对中性调整、球头面与阀体内锥面的相对转动控制、拧紧力矩及拧紧对中的应力控制等。2 种因素的综合作用是造成不同漏率值的主要原因[13-16]。

5 结束语

本文对发动机螺接头的漏率随时间变化规律进行了试验研究，结果表明，其漏率随时间的增加，大体呈现出4 种变化趋势。零部件加工因素及装配操作因素会导致螺接头漏率值不尽相同，这2 种因素的综合作用是造成4 种漏率变化规律的主要原因。

（References）

[1]周鑫.球面密封结构的漏率预估[J].宇航学报, 2007, 28(3)∶762-766 Zhou Xin.Leak rate prediction of orbicular joint[J].Journal of Astronautics, 2007, 28(3)∶762-766

[2]韩冲, 张勇.导管连接件球头-锥面结构密封性能研究[J].润滑与密封, 2012(10)∶1-2 Han Chong, Zhang Yong.Research on sealing property of globe cone joint for pipeline[J].Lubrication Engineering, 2012(10)∶1-2

[3]中国航空材料手册编委会.中国航空材料手册[M].北京∶中国标准出版社, 2001∶15-23

[4]顾伯勤, 李新华, 田争.静密封设计技术[M].北京∶中国标准出版社, 2004∶1

[5]张剑锋, 周志芳.摩擦磨损与抗磨技术[M].天津∶天津翻译出版公司, 1993∶58-70

[6]吴孝俭, 闫荣鑫.泄漏检测[M].北京∶机械工业出版社, 2009∶97-100

[7]QJ 3088 1999 正压标准漏孔校准方法[S], 1999

[8]GJB/J 5366 2005 正压漏孔校准规范[S], 2005

[9]杨桂通.弹塑性力学引论[M].北京∶高等教育出版社, 1989∶43-99

[10]卓卫东.应用弹塑性力学[M].北京∶科学出版社, 2004∶82-106

[11]陈惠发, 萨里普A F.弹性与塑性力学[M].余天庆, 王勋文, 刘再华, 译.北京∶中国建筑工业出版社, 2004∶211-261

[12]徐秉业.塑性力学[M].北京∶高等教育出版社, 1989∶21-26

[13]蔡仁良, 顾伯勤, 宋鹏云.过程装备密封技术[M].北京∶化学工业出版社, 2002∶1-12

[14]Guillermo E.Finite element analysis of failure response behavior bolts in concrete[J].Nuclear Engineering and Design, 1998, 179(2)∶245-252

[15]Chung K F, lpK H.Finite element investigation on the structural behavior of cold-formed steel bolted connections[J].Engineering Structures, 2001, 23(9)∶1115-1125

[16]王勇, 闫荣鑫.应力松弛对球头密封结构漏率影响的分析[J].航天器环境工程, 2009, 29(5)∶455-457 Wang Yong, Yan Rongxin.Effect of stress relaxation on the leak rate of the orbicular seal joint[J].Spacecraft Environment Engineering, 2009, 29(5)∶455-457