考虑负荷类型的含分布式电源系统对配电网电压的影响

田书，王丽

（河南理工大学 电气工程与自动化学院，河南 焦作 454000）

分布式电源（DG）以并网形式接入配电网运行时，使得配电网从原有的单一电源供电系统成为具有分散电源的多电源系统，给现有的电力系统带来了诸如电压、电能质量、继电保护、可靠性等一系列的问题[1-4]。潮流计算是分析这些问题的基础。

传统配电网潮流计算中，负荷大多采用恒功率模型。随着越来越多的诸如变频调速等电压敏感性负荷[5-6]接入系统中，这类负荷模型不能真实地反映负荷的性质，从而无法准确地反映电网的潮流分布状况。文献[7]对于传统的模态分析方法进行改进，考虑了负荷类型的变化，结果表明系统的电压稳定裕度得到提高。文献[8]指出在电压稳定临界区域电压陡降时，应计及阻抗负荷和恒电流负荷对静态电压稳定的作用，使用综合负荷进行计算。因此，为了准确分析DG并网所带来的影响，有必要研究计及负荷类型含分布式电源配电网潮流计算。

目前，对于含分布式电源配电网潮流计算，大致有以下几种研究。文献[9-12]采用恒功率模型表示馈线上的负荷，定量分析了分布式发电对配电网电压分布的影响。文献[13]研究了DG并网后对电压的支撑能力，分析了DG接入位置及其接入方式不同对电压暂降所带来的影响。文献[14]研究了分布式电源接入放射状链式配电网络前后负荷节点电压的变化。以上文献都将负荷类型统一，采用单一的负荷模型，忽略了实际负荷情况。

基于上述分析，本文提出了改进牛顿法。该算法采用矩阵分裂以及矩阵求逆运算的松弛方法，使求解过程简单、快捷，有效地提升了算法效率，削弱了负荷类型变化对迭代次数以及迭代时间的影响。运用Matlab 软件，采用不同的负荷类型仿真33节点系统，结合DG接入变化的实验，总结了负荷类型对含DG系统电压的影响。

1 考虑负荷类型的配电网潮流计算改进牛顿法

不同的负荷点应采取不同负荷性质所占比例来模拟其实际负荷情况。近些年，电压敏感性负荷类型在系统负荷中所占的比例逐年增加，因此有必要研究其负荷对配电网的影响，采用恒功率、恒阻抗和恒电流3种类型结合起来的ZIP负荷模型[13]来表示。

式中，P0、Q0为在额定电压下的负荷有功功率和无功功率；U0为额定电压；aP（aQ）、bP（bQ）、cP（cQ）为负荷有功功率（无功功率）的系数，分别代表与电压平方成正比的恒定阻抗消耗的功率所占的比例、与电压成正比的恒电流负荷相对应的功率所占的比例、恒功率分量所占的比例，各系数之间满足aP+bP+cP=1，aQ+bQ+cQ=1。

传统的基于极坐标的牛顿拉夫逊法如下：

当考虑ZIP模型时，潮流方程将包括随电压变化的有功和无功两部分，雅克比矩阵中的元素N，L中应考虑电压变化部分

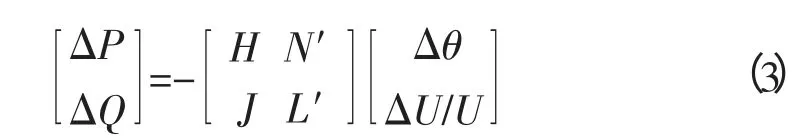
当考虑ZIP模型时

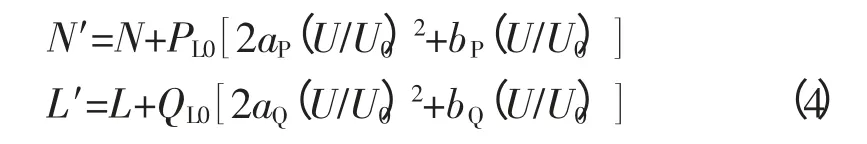
增加的元素使得传统的牛顿潮流计算过程更加复杂、费时。为克服此问题，可以对雅克比矩阵进行分裂，采用矩阵求逆运算的松弛方法，构造出一种新的潮流计算法。

定义：

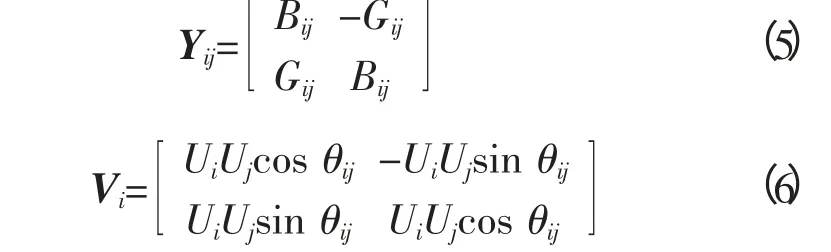
其中，αi=PLi0└2aP（Ui/Ui0）2+bP（Ui/Ui0）┘，βi=QLi0└2·aQ（Ui/Ui0）2+bQ（Ui/Ui0）┘

则雅克比矩阵M可以写成

式（10）中，Y为节点导纳矩阵；JD为新构造的对角矩阵；V为新构造的矩阵。

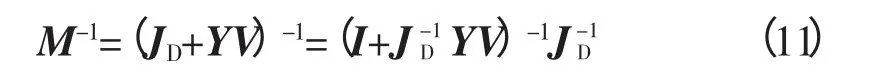
由文献[15]给出的方法可以推断出谱半径ρ（J－1D·YV）<1，在这种情况下利用矩阵求逆运算的松弛方法，可以近似得到

将式（12）代入方程（3）可得

式（13）即为本文所提出的改进牛顿法潮流计算。很显然方程（13）的求解比方程（3）容易，它无需直接形成配电网的雅可比矩阵，也无需对雅可比矩阵进行费时的求逆运算，而是直接利用了解裂后的矩阵进行求解。求解过程中因计及负荷类型而增加的元素，不会增加计算的复杂程度。

2 各种DG在改进算法中的潮流计算模型

传统配电网在潮流计算中一般取平衡节点、PQ节点以及PV节点，而DG由于其运行和控制方式的特点，需要对其节点类型进行考虑，得出相应的潮流计算模型。由风力发电、太阳能光伏、燃气轮机、燃料电池等发电模式，总结出可以将DG视为PQ节点、PV节点、PI节点和PQ（V）节点。

以上类型的DG在改进牛顿潮流法中的处理方式如下：1）P、Q均恒定的PQ型DG，只需将其无功和有功在迭代中用负数表示，其他不变；2）P恒定、V恒定的PV型DG，其有功功率是给定值，将PV节点转换成求注入无功的大小，在每次迭代过程中，根据灵敏度矩阵和PV节点电压幅值不匹配量对无功进行修正；3）P恒定、电流幅值I恒定的PI型DG，其有功功率恒定，只需利用Q（I，U）关系式，将最新的电压迭代值代入即可得到无功功率，计算出的无功以及给定的有功都取负值；4）P恒定、Q随电压变化的PQ（V）型DG，只需在每次迭代过程中，由最新电压值代入Q=f（U）关系式中计算出新的无功功率，最终处理与PQ型DG类似。

3 算例分析

以图1的IEEE33 节点系统为例进行仿真，该系统网络参数见文献[16]。基准功率为10 MW，基准电压为12.66 kV ，计算精度设为10-4，节点1为平衡节点，其余节点为负荷节点。

图1 IEEE 33节点测试系统Fig. 1 IEEE 33 bus system

3.1 无DG测试

对比分析算法的收敛性和计算速度，系统原始条件保持不变，将本文所提算法与传统牛顿法进行了对比测试。测试结果如表1所示。

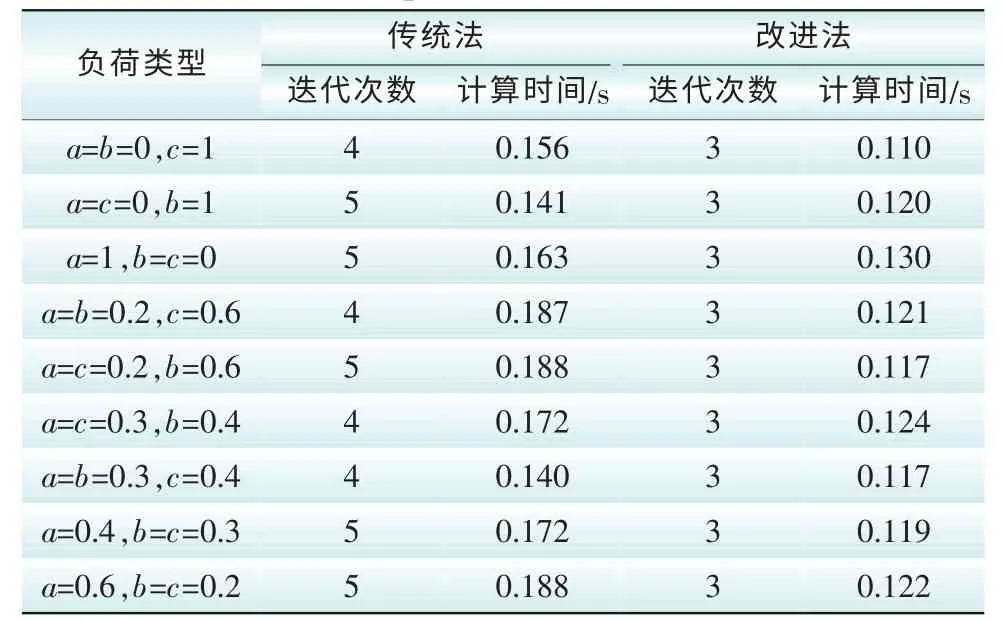
表1 传统法与改进法对比Tab. 1 Comparison of the conventional method and the improved method

从表1可以看出，本文所提出的改进牛顿计算方法与传统的经典牛顿法相比，不需对节点导纳矩阵进行求逆运算，因此在迭代次数以及计算时间上更占优势。改进算法的迭代次数更加稳定，受负荷类型变化的影响较小。

3.2 DG接入对系统电压的影响

在33节点系统中接入的各种类型DG参数如下：1）PQ型DG：有功功率P=0.042 4 pu，无功功率Q=0.057 pu；2）PQ（V）型DG：同步发电机的有功输出P=0.424 pu，Xd=0.017 pu，异步发电机的有功输出P=0.424 pu，x=0.168 pu，xP=3.86 pu；③PV型DG：有功功率P=0.042 4 pu，V=1.0 pu；④PI型DG：有功输出P=0.424 pu，I=0.012 pu。

4种类型的DG均采用2种接入方案，以便分析对比。方案1为节点2处接入DG，方案2为节点18处接入DG。所得结果如图2—6所示。从图中可得到DG接入对考虑负荷类型配电网电压影响的变化规律。

图2 PQ恒定型DG接入时电压波形图Fig.2 Voltage profiles with access of the DG of the PQ type

图3 PQ（V）型DG（发出无功）接入时电压波形图Fig. 3 Voltage profiles with access of the DG of the PQ（V）（generating reactive power)

1）接入PQ型DG后，随着恒阻抗负荷所占比例的增加，系统各节点（平衡节点除外）电压增加，馈线末端节点电压增加幅度较其他节点高。方案1的系统电压小于方案2，表明DG的接入使得系统整体电压得到提升，且提升的幅值与其接入位置密切相关。DG接入越靠近馈线末端，节点电压提升越高，而靠近馈线首端，系统电压变化较小。

图4 PQ（V）型DG（吸收无功）接入时电压波形图Fig. 4 Voltage profiles with access of the DG of thePQ（V）type (absorbing reactive power)

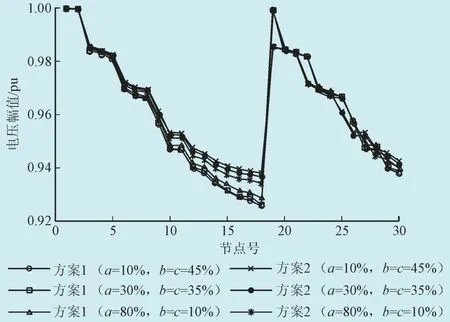
图5 PV型DG接入时电压波形图Fig.5 Voltage profiles with access of the DG of the PV type

图6 PI型DG接入时电压波形图Fig.6 Voltage profiles with access of the DG of the PI type

2）接入PQ（V）型DG后，系统各节点（平衡节点除外）电压随着恒阻抗负荷所占比例的增加而提高，在馈线末端电压提升幅度比该馈线其他节点高。以同步发电机接入时（发出无功），方案1节点电压均低于方案2，表明此类型DG对系统各节点电压起到提升作用，电压提升程度是接入位置越接近馈线末端越好。以异步发电机接入时（吸收无功），方案1节点电压均大于方案2，表明此类型DG接入会降低系统电压，且接入位置越接近馈线末端电压降低越多。

3）接入PV型DG后，随着恒阻抗负荷所占比例的增加，系统节点电压不再有明显的提升。方案1和方案2电压分布比较可知，DG的接入不一定提升系统节点电压，可能会使得节点电压降低。针对PV型DG应选择合适的接入位置，使其可以较好地改善系统电压。

4）接入PI型DG后，随着恒阻抗负荷所占比例的增加，系统节点电压得到明显的提升。从图6可以看出，PI型DG接入可以提高系统电压水平，其对电压的影响与PQ型节点类似，这是由于当注入的有功一定时，可以由电流幅值计算出无功输出，最终相当于向系统输入了一定的有功和无功。

4 结论

算例结果表明，本文的改进牛顿法迭代次数和迭代时间较少，且当负荷类型发生变化时，算法效率受影响较小，具有较强的实用性。考虑负荷类型后，提高了对系统分析的精确性，使结果更加符合实际的运行情况。

将分布式电源归结为PQ、PQ（V）、PV、PI 4种类型，并构建相应的潮流计算模型，使其可以用于在改进牛顿法中求解DG接入对配电网的影响。

通过考虑负荷类型变化分析DG接入后的影响，得到以下结论：恒阻抗负荷比例的增加，有助于提升系统电压水平，且馈线末端节点的提升幅度较该馈线上其他点大。当接入PV型DG后提升系统电压作用远小于其他3种类型的DG。

以PQ型、同步发电机、PI型为接口接入的DG均提升系统电压；以异步发电机为接口接入的DG会降低系统电压；接口为PV型的DG可能提升也可能降低系统电压。从改善系统电压的角度来看，应根据DG接口的类型选择合适的接入位置。

[1] 王建，李兴源，邱晓燕，等. 含有分布式发电装置的电力系统研究综述[J]. 电力系统自动化，2005，29（24）: 90-97.WANG Jian，LI Xingyuan，QIU Xiaoyan. Power system research on distributed generation penetration[J]. Automation of Electric Power Systems，2005，29（24）: 90-97（in Chinese）.

[2] SLOOTWEG J G，KLING W L. Impacts of distributed generation on power system transient stability[C]// Power Engineering Society Summer Meeting，July 25，2002 IEEE，Chicago，USA，2002（7）：862-867.

[3] 庄园，贺海，杨晓慧，等. 含分布式电源优化调度的配电网络重构[J]. 电网与清洁能源，2012，28（11）: 13-18.ZHUANG Yuan，HE Hai，YANG Xiaohui，et al. Distribution network reconfiguration with optimal allocation of distributed generation[J]. Advances of Power System &Hydroelectric Engineering，2012，28（11）: 13-18 （in Chinese）.

[4] ZHANG F，CHENG C S. A modified newton memod for radial distribution system power flow analysis[J]. IEEE Transactions on Power Systems，1997，12（1）: 389-397.

[5] 陈晓静，陈武，肖先勇，等. 电压敏感负荷电压凹陷敏感性估计[J]. 四川电力技术，2008，31（5）: 17-19，72.CHEN Xiaojing，CHEN Wu，XIAO Xianyong. The sensitivity stochastic assessment of equipment due to voltage sag[J]. Sichuan Electric Power Technology，2008，31（5）:17-19，72（in Chinese）.

[6] 彭俊臻，宋萌，束洪春，等. 饱和铁心型超导可控电抗器对线路工频过电压的影响分析[J]. 高压电器，2013，49（9）: 80-84.PENG Junzhen，SONG Meng，SHU Hongchun，et al.Analysis of the influence of saturated core superconducting controllable reactor on line power frequency overvoltage[J].High Voltage Apparatus，2013，49（9）:80-84（in Chinese）.

[7] 韩光，丁晓群，侯学勇，等. 考虑负荷类型和发电机节点的模态分析[J]. 电气应用，2007，26（1）: 53-55，92.HAN Guang，DING Xiaoqun，HOU Xueyong. Modal analysis considering load model and generator node[J].Electrotechnical Application，2007，26（1）: 53-55，92（in Chinese）.

[8] 王冰，游振华，韩学军，等.考虑负荷静态电压特性的重负荷节点静态电压稳定分析[J]. 继电器，2007，35（11）:21-25.WANG Bing，YOU Zhenhua，HAN Xuejun，et al. Steadystate voltage stability analysis of heavy load node considering the steady-state load characteristics[J]. Relay，2007，35（11）: 21-25（in Chinese）.

[9] 王志群，朱守真，周双喜，等. 分布式发电对配电网电压分布的影响[J]. 电力系统自动化，2004，28（16）: 56-60.WANG Zhiqun，ZHU Shouzhen，ZHOU Shuangxi，et al.Impacts of distributed generation on distribution system voltage profile[J]. Automation of Electric Power Systems，2004，28（16）: 56-60（in Chinese）.

[10] 陈海焱，段献忠，陈金富. 分布式发电对配网静态电压稳定性的影响[J]. 电网技术，2006，30（19）：27-30.CHEN Haiyan，DUAN Xianzhong，CHEN Jinfu. Impacts of distributed generation on steady state voltage stability of distribution system[J]. Power System Technology，2006，30（19）：27-30（in Chinese）.

[11] 白茜. 分布式发电对配电网电压调整作用的机理研究[D]. 北京: 华北电力大学，2007.

[12] 孙秋野，李钟旭，杨珺，等. 分布式发电对配电网静态电压分布的影响[J]. 东北大学学报：自然科学版，2010，31（8）: 1074-1077.SUN Qiuye，LI Zhongxu，YANG Jun，et al. Impact of distributed generation on static voltage profile in distribution networks[J].Journal of Northeastern University：Natural Science，2010，31（8）: 1074-1077（in Chinese）.

[13] 唐小波，徐青山，唐国庆，等. 含分布式电源的配网潮流算法[J]. 电力自动化设备，2010，30（5）: 34-37.TANG Xiaobo，XU Qingshan，TANG Guoqing. Power flow algorithm for distribution network with distributed generation[J]. Electric Power Automation Equipment，2010，30（5）: 34-37（in Chinese）.

[14] 章健. 电力系统负荷模型与辨识[M]. 北京：中国电力出版社，2007.

[15] 李玉清. 判定矩阵谱半径小于1的一种方法[J]. 高等数学研究，2012，15（1）: 75-76.LI Yuqing. A test for spectral radius of matrixes[J]. Studies in College Mathematics，2012，15（1）:75-76（in Chinese）.

[16] 王守相，王成山. 现代配电系统分析[M]. 北京: 高等教育出版社，2007.