复变函数中定积分的计算
王华阁
(新乡医学院 基础医学院,河南 新乡 453003)
在《复变函数与积分变换》教材中,在复变函数这部分内容中,定积分的计算方法多种多样,我们可以针对具体的定积分题型,选择合适的积分方法。 在这里,我们针对每种积分类型的特点,通过相应的例题,给出具体的解法。
1 参数方程法
对于积分曲线C 为不封闭曲线的定积分,可以考虑参数方程法进行计算。 用参数方程法计算定积分可以根据不同情况由两种方法进行计算。
1.1 通过化为两个二元实变函数的积分进行计算
由z=x+iy,f(z)=u(x,y)+iv(x,y),可得
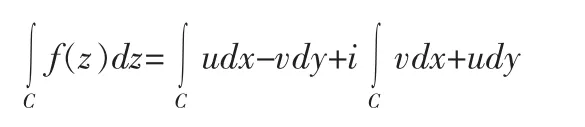
解:设f(z)=z2=(x2-y2)+2ixy,u=x2-y2,v=2xy。
设曲线C1的参数方程为
1.2 化为参变量的定积分进行计算
对于例1,我们可以化为参变量的定积分,按照这种方法进行计算。
解:设曲线C1的参数方程为
从而,

2 根据柯西定理及推论进行计算
2.1 定理1(柯西定理)
设C 是一条简单正向闭曲线,f(z)在以C 为边界的有界闭区域D 上解析,则
2.2 定理2(柯西定理推论)
设D 为由外线路C0和内线路C0,C1,C2,…,Cn围成的多连通 区 域,f(z)在D 内及边界曲线C0,C1,C2,…,Cn上解析,则这里C 为多连通区域D 的所有正向边界,方向为C0取逆时针方向,ck(k=1,2,L,n)取顺时针方向。
例3:C 为矩形区域0≤x≤3,0≤y≤2 的正向边界, 证明:
证明:在矩形区域里做正向圆周R:z-(2+i)=reiθ(θ:2π→0),则在图中的复连通区域内解析,从而根据柯西定理的推论有:
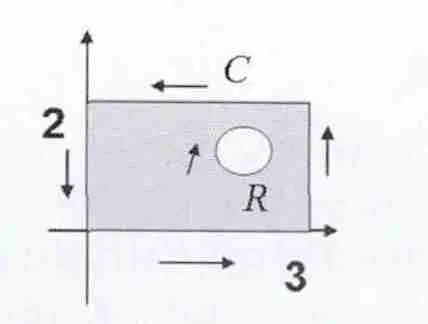
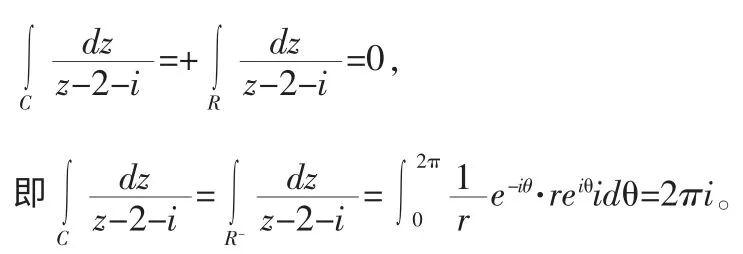
3 根据柯西积分公式进行计算
定理3:设f(z)在简单正向闭曲线C 及所围区域D 内处解析,z0为D 内任一点,则我们把这个公式称为柯西积分公式。
定理3 说明f(z0)可由函数在C 上的积分来确定,但实际上,我们通常把这个公式进行变形,可以用这个公式来计算积分
用柯西积分公式进行计算时, 先对曲线C 的解析性做判断,然后按照下列步骤进行:首先注意C 应该为正向闭曲线,若f(z)在C 所围的区域里解析,则根据柯西定理,若f(z)在C 所围的区域里不解析,再分以下两种情况:
(1)当f(z)有一个不解析点z0时,考虑能否把f(z)化成,其中g(z)在C 内解析,则由柯西积分公式可得,
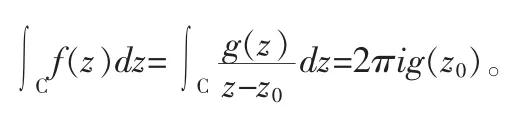
(2)当f(z)有n 个不解析点时,做以不解析点为圆心的正向圆周C1,…,Cn,半径足够小,则由柯西定理的推论,

解:当C 为|z-2|=1 时,
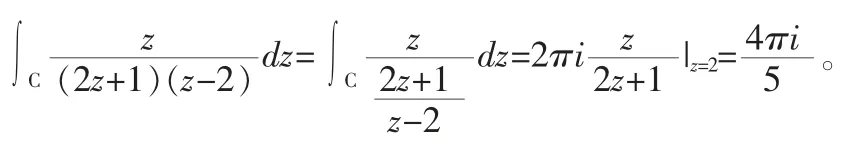
4 利用高阶导数公式进行计算
定理4:设f(z)在简单正向闭曲线C 及其所围区域D 内处解析,z0为D 内任一点, 则0,1,2…)
解:因为cosπz 在复平面上处处解析,所以由定理4,
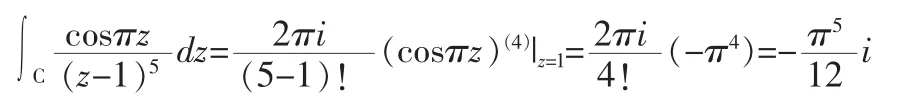
5 利用留数定理进行计算
定理5(留数定理):设D 是复平面上的一个有界闭区域,若f(z)在D 内除有限个孤立奇点z1,z2,…,zn外处处解析,且它在D的边界C 上也解析,则
利用留数定理计算定积分的步骤:
(1)找出C 所围区域内f(z)的所有孤立奇点,设为z1,z2,…,zn。
(2)对每个孤立奇点zi,分别求Res(f,zi)。
(3)利用留数定理求定积分:
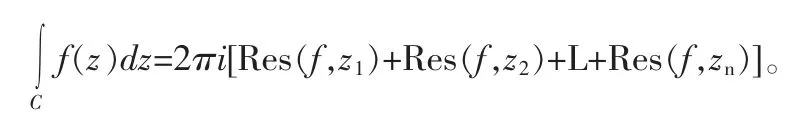
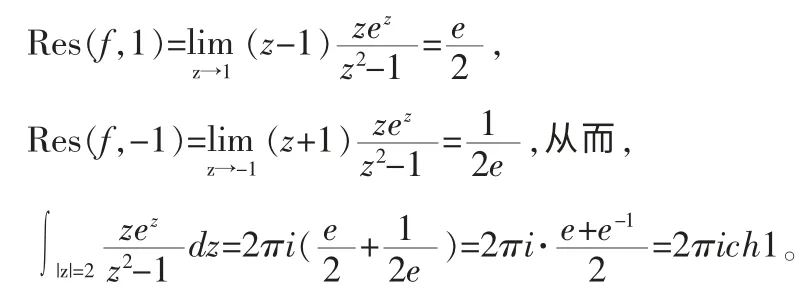
[1]苏变萍,陈东立.复变函数与积分变换[M].北京:高等教育出版社,2010.
[2]同济大学数学系.高等数学[M].北京:高等教育出版社,2007.
[3]钟玉泉.复变函数论[M].北京:高等教育出版社,1988.

