厚层河道砂体地应力分布影响因素分析
祖克威,曾联波,2,刘喜中,张俊辉,赵向原,刘国平
(1.中国石油大学 (北京)地球科学学院,北京102249;2.中国石油大学油气资源与探测国家重点实验室,北京102249)
0 引言
地应力是客观存在的一种自然力,通常是指赋存于地壳中的内应力[1]。主要由上覆岩层重力、地层压力、构造应力、孔隙流体压力等构成。现今地应力是相对古应力而言,是指地层目前的应力状态。地应力与储集层的性质和油气运移、聚集都有着密切的关系[2~5]。只有及时掌握现今地应力场的变化,才能合理布置注采井网、定量控制采油量和注水量及优化压裂设计与施工[6~7]。
中国东部中新生代含油气盆地已开发的油田中,河流相储集层的油气地质储量占40%以上[8]。随着油气开发的进一步深入,相关资料表明河道砂体现今地应力的大小和方向与围岩有着明显的差异性,这种差异性严重影响了对油气资源的开发和管道的部署。因此,对河道砂体及围岩开展现今地应力分析,直接关系到勘探开发工作的成败[9],具有重要的理论意义和实践价值。
对现今地应力影响因素的研究,前人已经开展了大量工作,沈海超等[10]和孙礼建等[11]利用数值模拟法研究断层对地应力的影响,提出边界应力条件和断层介质性质是影响断层附近地应力状态的敏感因素。在深部,同一高程,断层上盘的主应力大于断层下盘[12],并且断裂带附近应力随时间发生变化[13~15]。谭成轩等[16]和秦忠诚等[17]在实测资料的基础上,运用三维数值模拟分析讨论了地形地貌对地应力状态的影响,并提出构造应力面的概念。国内外一些地质学家通过实验和理论分析提出岩体结构和力学性质与地应力之间有一定的关系,但缺乏定量化[18~22]。此外,孔隙中的流体和地温梯度都会引起地应力的改变,但是对地应力状态的影响相对较小[23]。然而针对沉积微相内现今地应力状态的主控因素分析,前人尚未开展工作。
本文利用数值模拟方法对平面河流相数值模型内现今地应力的影响因素进行分析,重点研究河道及周围岩石介质的力学性质差异、边界条件和河流形态对河道内现今地应力方向及大小的影响,并运用实例说明该研究在河流相储层开发中的应用。
1 模型的建立
本次研究中的数值模拟利用有限元软件ANSYS实现。在建立模型时假设:①模型为平面应变状态;②河道砂体及周围岩体为均匀的弹性各向同性材料;③本次模拟为单条河道内局部段,因而模型中的河道为矩形条带;④边界应力为区域应力,作用方向垂直于边界。
参数定义:①边界应力σ1为区域水平最大主应力,σ2为区域水平最小主应力;②河道砂体的弹性模量为E1,泊松比为υ1;③河道周围岩体弹性模量为E2,泊松比为υ2;④河道走向与区域最大水平主应力的夹角为θ。
采用平面模型,主体部分为一矩形岩体,中间为一个贯通性河道,河道长1000 m,宽250 m。在河道外部施加一个矩形边框作为区域边界。本次模拟的岩石力学参数由室内岩石力学实验获得,将河道处理成弹性模量较大材料,而河道围岩和外部边框处理成弹性模量相对较小塑性较强的材料。河道走向与区域水平最大水平主应力的夹角为θ。模型一侧受到垂直于边界的区域平面应力场的作用,模型另一侧被约束 (见图1)。对不同边界条件的模型分析时,其他边界条件固定,模型仅对单一因素进行相应的改变。

图1 模型的几何条件和边界条件Fig.1 Geometry and boundary conditions of the model
2 结果分析
为了便于分析,假定初始区域水平最大主应力σ1为64 MPa,区域水平最小主应力σ2为50 MPa,河道砂体初始弹性模量E1为40 GPa,泊松比υ1为0.22,周围岩体初始弹性模量E2为20 GPa,泊松比υ2为0.36,河道走向与区域水平最大主应力方位夹角为30°。对不同的因素分析,仅改变相应的数值,其他初始值不变。
2.1 弹性模量对地应力的影响
河道砂体及周围岩体弹性模量对地应力的影响可以分为两方面展开分析:①E1/E2不变,同比例增加河道砂体和周围岩体的弹性模量;②E2不变,逐渐增加河道砂体的弹性模量E1。
2.1.1 保持弹性模量比不变
在不改变E1/E2比值的前提下,同比例增加河道弹性模量和围岩弹性模量,模拟结果表明,河道与围岩弹性模量的差异会引起河道内部地应力方向发生偏转,其偏转方向趋于与河道走向平行,但是随着E1与E2同比例增加,其对河道内及围岩的地应力大小和方向的变化几乎没有影响。
2.1.2 保持围岩弹性模量不变
在保持围岩弹性模量E2为20 GPa不变的情况下,将河道砂体的弹性模量E1从20 GPa变为100 GPa,并对变化过程中河道内地应力方向和大小的变化进行分析,结果表明,随着弹性模量比的增加,河道内地层地应力方位较为统一,最大主应力方向与区域最大主应力方向之间的夹角也随着增加,与河道走向之间的夹角减小,河道内最大主应力方位与周围岩体最大主应力之间的夹角增加 (见图2,图3);同时河道内最小主应力值和最大主应力增加,最大主应力的增加幅度大于最小主应力增加幅度,差应力增加 (见图4,图5)。

图2 不同E1/E2的河道砂体最大水平主应力方位对比图 (黑色矩形内为河道砂体)Fig.2 A comparison diagram of the maximum horizontal principal stress directions in channel sandstone with different E1/E2
改变区域水平最大主应力,河道泊松比,河道走向同区域最大主应力夹角等初始假定值进行分析,结论相同。
综上所述,河道与周围岩石的弹性模量比对河道内地应力的方向和大小影响明显,是影响河道内地应力大小和方向的敏感因素。

图3 河道砂体最大主应力方向同E1/E2的关系Fig.3 Relationship between the direction of maximum horizontal principal stress in channel sandstone and E1/E2
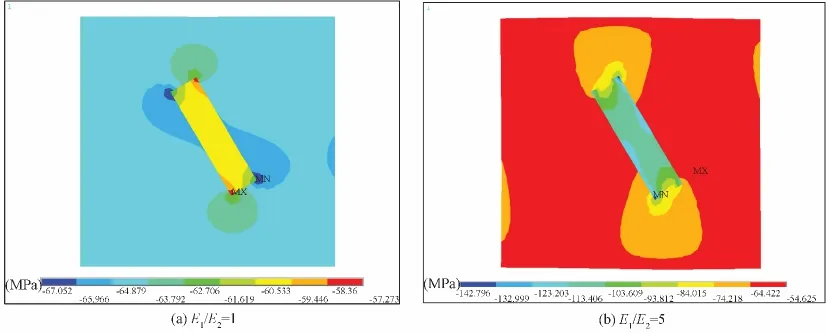
图4 不同E1/E2的河道砂体最大水平主应力大小对比Fig.4 A comparison diagram of the maximum horizontal principal stress values in channel sandstone with different E1/E2

图5 河道砂体地应力大小与E1/E2的关系Fig.5 Relationship between horizontal principal stress in channel sandstone and E1/E2
2.2 泊松比对地应力的影响
河道砂体及周围岩体泊松比对地应力的影响可以从两方面展开分析:①υ1/υ2不变,同比例增加河道砂体和周围岩体的泊松比;②υ2不变,逐渐增加河道砂体的泊松比υ1。
2.2.1 保持河道和周围岩石泊松比比值不变
以υ1/υ2=0.61为例进行分析,结果表明,当河道砂体与周围岩石的泊松比以同比例增大时,河道内及周围岩石的地应力方向基本不变,水平最大主应力和最小主应力仅发生微小变化。
2.2.2 改变河道和周围岩石泊松比比值
模拟过程中,假定周围岩石的泊松比υ2保持0.36不变,河道砂体泊松比υ1从0.18变为0.36,观察河道及周围岩石地应力方向及大小的变化。模拟结果表明,随着υ1/υ2值从0.5变为1.0,河道内最大主应力方向基本不变 (见图6),最小和最大主应力值略微减小,最大主应力减小梯度大于最小主应力减小梯度,因而差应力减小 (见图7)。改变水平最大主应力、河道弹性模量和河道走与同水平最大主应力方向等初始假定参数分析,得到的结论相同。

图6 河道砂体最大主应力方向与υ1/υ2的关系Fig.6 Relationship between the direction of maximum horizontal principal stress in channel sandstone and υ1/υ2

图7 河道砂体地应力大小与υ1/υ2的关系Fig.7 Relationship between horizontal principal stress in channel sandstone and υ1/υ2
综上可知,河道和周围岩石介质的泊松比变化对河道内地应力状态的影响很小,因而泊松比不是影响河道内地应力状态的敏感因素。
2.3 河道走向对地应力的影响
假定其他初始条件不变,分析当河道走向与水平最大主应力的夹角θ从0°增大到90°时河道砂体地应力状态的变化情况。结果表明,在其他条件不变时,河道砂体地应力方位较为统一,其最大主应力方向与区域最大主应力方向及围岩最大主应力方向夹角存在一个分界角度,其值约45°。当θ<45°时,随着θ增加,河道砂体最大主应力方向与区域最大主应力方向及围岩最大主应力方向夹角随之增加;当θ>45°时,随着θ的增大,河道砂体最大主应力方向与区域最大主应力方向及围岩最大主应力方向夹角随之减少 (见图8)。

图8 河道内最大主应力方向与θ的关系Fig.8 Relationship between the direction of maximum horizontal principal stress in channel sandstone andθ
但河道砂体地应力值的变化不存在临界角度,即随着θ增加,河道内最小主应力增加,最大主应力减小,差应力减小 (见图9)。改变区域最大主应力值,河道弹性模量和泊松比等初始假定条件,结论相同。因而,河道走向与区域最大主应力方向夹角为影响河道内现今地应力状态的敏感因素。
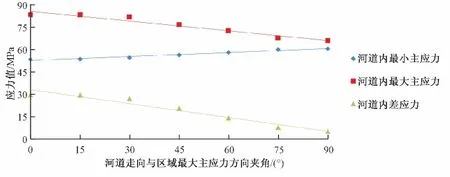
图9 河道内地应力大小同θ的关系Fig.9 Relationship between horizontal principal stress in channel sandstone andθ
2.4 区域边界应力比对地应力的影响
在其他初始边界不变的前提下,分析当σ1从50 MPa变为100 MPa,即σ1/σ2值从1.0增大到2.0时河道内地应力变化的情况。模拟结果表明,随着σ1/σ2的增大,河道内最大主应力方向与区域最大主应力方向和围岩最大主应力方向间夹角减小,与河道走向的夹角增大(见图10);河道内最小主应力值和最大主应力值增加,最大主应力值增加速度较快,差应力增加 (见图11)。
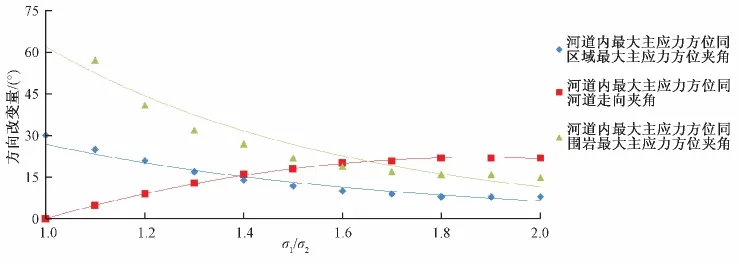
图10 河道砂体最大主应力方向与σ1/σ2的关系Fig.10 Relationship between the direction of maximum horizontal principal stress in channel sandstone and σ1/σ2

图11 河道砂体地应力大小与σ1/σ2的关系Fig.11 Relationship between horizontal principal stress in channel sandstone and σ1/σ2
改变河道弹性模量、泊松比以及区域地应力方向等初始假定值进行分析,结论相同,因而边界应力比是影响河道内现今地应力方向的主要因素。
3 应用实例
以渤海南部某区块为例,该区中部主要为浊积水道,外部为水道漫溢和湖盆泥 (见图12),利用古地磁法、微地震法和钻孔崩落信息分别对浊积水道内和水道外部湖盆泥远离断层处的现今地应力方位进行大量的测量统计,结果表明浊积河道内最大水平主应力平均方位为120°,湖盆泥中最大水平主应力平均方位为70°。数值模拟结果表明河道内与周围岩体地应力方位的差异主要为由沉积相差异引起的岩石物理性质的变化。
因此,在对该区块进行压裂时,河道内人工裂缝走向与周围岩体人工裂缝走向及区域最大水平地应力方向相比会发生偏离,尤其在断层附近,叠加断层的影响会使得局部地应力方位与区域地应力方位偏离严重。因此井网布置等开发方案制定时需考虑不同沉积相对地应力方向和大小的影响。例如,河道内的注采井网,应根据地应力方向进行相应调整,以增强注水开发效果。而目前人们往往对地应力场分布的复杂性认识不够,开发方案的制定和实施没有考虑河道内和周围岩体现今地应力分布规律的差异性。
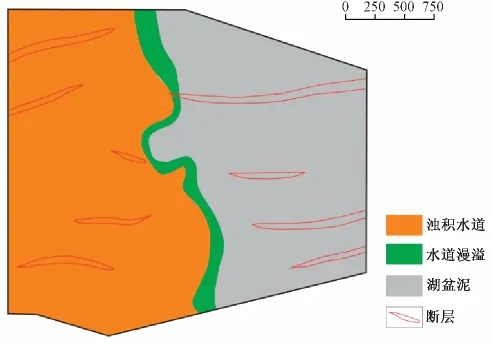
图12 渤海南部某区块沉积相图Fig.12 The sedimentary facies map of some block in Bonan zone
4 结论
河道砂体现今地应力的特征与周围岩体地应力特征具有明显不同,河道及周围岩石介质的力学性质差异、边界条件和河流形态均对河道内现今地应力方向及大小产生影响,不同影响因素的影响程度不同。
河道介质受到区域地应力作用,河道内部地应力方向发生改变,地应力旋转方向趋于与河道走向小角度相交。河道介质与周围岩体的弹性模量比值、河道走向同区域主应力方向夹角及边界应力比是影响河道内地应力方向的敏感因素。当贯穿的河道走向较为平直时,河道内地应力方向较为一致,随着边界条件的改变,与区域主应力方向相比,河道内主应力方向均有不同程度的变化,变化的幅度为0°—30°;河道内地应力方向与河道走向夹角的变化幅度为0°—90°;河道内部地应力方向与周围岩体地应力方向夹角的变化幅度为0°—90°。
河道介质同周围岩体的弹性模量比值、河道走向与区域主应力方向夹角及边界应力比是影响河道内地应力大小的敏感因素。
本次研究结果可用于解释在远离断层部位,相邻沉积相地应力方向和大小差异较大的原因,为不同沉积模式下储层地应力的进一步研究提供了参考依据。建议在此基础上建立三维模型,分析垂向上不同河道组合形式下,地应力的分布特点。
[1] 谢润成,周文,邓虎成,等.现今地应力场特征评价一体化研究[J].石油钻采工艺,2008,30(4):32~35.XIE Run-cheng,ZHOU Wen,DENG Hu-cheng,et al.Integrated research methods of in-situ stress field characteristics[J].Drilling& Production Technology,2008,30(4):32~35.
[2] 王连捷,张利容,袁嘉音,等.地应力与油气运移[J].地质力学学报,1996,2(1):3~10.WANG Lian-jie,ZHANG Li-rong,YUAN Jia-yin,et al.Crustal stress and oil and gas migration [J].Journal of Geomechanics,1996,2(1):3~10.
[3] 曾联波,漆家福,王成刚,等.构造应力对裂缝形成于流体流动的影响 [J].地学前缘,2008,15(3):292~298.ZENG Lian-bo,QI Jia-fu,WANG Cheng-gang,et al.The influence of tectonic stress on fracture formation and fluid flow[J].Earth Science Frontiers,2008,15(3):292 ~298.
[4] Jean D R.Stress Fields:A key to oil migration [J].AAPG Bulletin,1980,65(1):74~85.
[5] Sibson R H.Crustal stress,faulting and fluid flow [C] //Parnell J.Geofluids:Origin,migration and evolution of fluids in sedimentary basins[M].Geological Society,1994,78:69~84.
[6] 楼一珊.地应力在油气田开发中的应用[J].石油钻探技术,1997,25(3):58~59.LOU Yi-shan.The application of in-situ stress in the oil and gas field development [J].Petroleum Drilling Techniques,1997,25(3):58~59.
[7] 葛洪魁,林英松,王顺昌.地应力测试及其在勘探开发中的应用 [J].石油大学学报:自然科学版,1998,22(1):94~99.GE Hong-kui,LIN Ying-song,WANG Shun-chang.In-situ stresses determination technique and its applications in petroleum exploration and development[J].Journal of the University of Petroleum,China,1998,22(1):94~99.
[8] 裘亦楠.中国陆相碎屑岩储层沉积学的进展[J].沉积学报,1992,10(3):16~23.QIU Yi-nan.Developments in reservoir sedimentology of continental clastic rocks in China [J].Acta Sedimentology Sinica,1992,10(3):16~24.
[9] 沈杨.河流相储层综合预测方法探索[J].沉积与特提斯地质,2002,22(4):84~91.SHEN Yang.An approach to the prediction of fluvial reservoirs[J].Sedimentary Geology and Tethyan Geology,2002,22(4):84~91.
[10] 沈海超,程远方,王京印,等.断层对地应力场影响的有限元研究[J].大庆石油地质与开发,2007,26(2):34~37.SHEN Hai-chao,CHENG Yuan-fang,WANG Jing-yin,et al.Study of finite element on effects of faults on ground stress field[J].Petroleum Geology& Oilfield Development in Daqing,2007,26(2):34~37.
[11] 孙礼健,朱元清,杨光亮,等.断层端部及附近地应力场的数值模拟 [J].大地测量与地球动力学,2009,29(2):7~12.SUN Li-jian,ZHU Yuan-qing,YANG Guang-liang,et al.Numerical simulation of ground stress field at ends and vicinity of a fault[J].Journal of Geodesy and Geodynamics,2009,29(2):7 ~12.
[12] 王有熙,邓广哲,曹晶.断层带对深部地压影响的数值模拟 [J].西安科技大学学报,2011,31(6):818~822.WANG You-xi,DENG Guang-zhe,CAO Jing.Numerical simulation of fault-zone’s influence on stress in deep mine [J].Journal of Xi’an University of Science and Technology,2011,31(6):818~822.
[13] 李方全,孙世宗,李立球.华北及郯庐断裂带地应力测量[J].岩石力学与工程学报,1982,1(1):73~86.LI Fang-quan,SUN Shi-zong,LILi-qiu.In-situ stress measurements in north China and Tancheng-Lujiang fault zone [J].Chinese Journal of Rock Mechanics and Engineering,1982,1(1):73~86.
[14] 高建理,丁建民,梁国平,等.龙羊峡水电站水压致裂应力测量 [J].岩石力学与工程学报,1990,9(2):134~145.GAO Jian-li,DING Jian-min,LIANG Guo-ping,et al.Hydraulic Fracturing Stress Measurements at the Longyangxia Water-Power Station [J].Chinese Journal of Rock Mechanics and Engineering,1990,9(2):134~145.
[15] Zoback M D,Tsukahara H,Hickman S.Stress measurements at depth in the vicinity of the San Andreas Fault:Implications for the magnitude of shear stress at depth [J].Journal of Geophysical Research:Solid Earth,1980,85(11):6157~6173.
[16] 谭成轩,孙炜锋,孙叶,等.地应力测量及其地下工程应用的思考 [J].地质学报,2006,80(10):1627~1632.TAN Cheng-xuan,SUN Wei-feng,SUN Ye,et al.A consideration on in-situ crustal stress measuring and its underground engineering application[J].Acta Geologica Sinica,2006,80(10):1627~1632.
[17] 秦忠诚,刘承论,赵祉业,等.地形及构造应力影响下初始地应力场的3D-FSM反演分析 [J].岩土力学,2008,29(7):1848~1852.QIN Zhong-cheng,LIU Cheng-lun,ZHAO Zhi-ye,et al.Back analysis of initial ground stresses by 3D-FSM considering influence of terrain and tectonic stress [J].Rock and Soil Mechanics,2008,29(7):1848 ~1852.
[18] 白世伟,李光煜.二滩水电站坝区岩体应力场研究[J].岩石力学与工程学报,1982,1(1):45~56.BAI Shi-wei,LIGuang-yu.Study on in-situ stress field of rock masses in dam area of Ertan hydropower plant[J].Chinese Journal of Rock Mechanics and Engineering,1982,1(1):45~56.
[19] 朱焕春,陶振宇.不同岩石中地应力分布 [J].地震学报,1994,16(1):49~63.ZHU Huan-chun,TAO Zhen-yu.The stress distribution of different rocks[J].Acta Seismologica Sinica,1994,16(1):49~63.
[20] 蔡美峰,王双红.地应力状态与围岩性质的关系研究[J].中国矿业,1997,6(6):38~41.CAI Mei-feng,WANG Shuang-hong.Relation between ground stress behavior and properties of surrounding rock [J].China Mining Magazine,1997,6(6):38~41.
[21] 景锋,盛谦,张勇慧,等.不同地质成因岩石地应力分布规律的统计分析[J].岩土力学,2008,29(7):1877~1883.JING Feng,SHENG Qian,ZHANG Yong-hui,et al.Statistical analysis of geostress distribution laws for different rocks[J].Rock and Soil Mechanics,2008,29(7):1877 ~1883.
[22] 秦向辉,谭成轩,孙进忠,等.地应力与岩石弹性模量关系试验研究[J].岩土力学,2012,33(6):1689~1695.QIN Xiang-hui,TAN Cheng-xuan,SUN Jin-zhong,et al.Experimental study of relation between in-situ crustal stress and rock elastic modulus [J].Rock and Soil Mechanics,2012,33(6):1689 ~1695.
[23] 周文,闫长辉,王世泽,等.油气藏现今地应力场评价方法及应用[M].北京:地质出版社,2007.ZHOU Wen,YAN Chang-hui,WANG Shi-ze,et al.The evaluation methodology and application of the reservoir present ground stress[M].Beijing:Geological Publishing House,2007.

