振动流化床结构动态分析

武继达，刘初升，赵跃民，李 珺

WU Ji-da1,3，LIU Chu-sheng1,3，ZHAO Yue-min2，LI Jun1,3

（1.中国矿业大学 机电工程学院，徐州 221116；2.中国矿业大学 化工学院，徐州 221116；3.中国矿业大学 盱眙矿山装备与材料研发中心，徐州 221116）

0 引言

振动流化床是一种新型的煤炭干法分选设备。其通过对普通流化床施加一定频率的振动，使煤炭颗粒作抛掷运动，从而促进物料的松散分层，增加物料与干燥气体的接触机会，提高了传热系数，有利于防止煤团黏结，提高流化效果[1～3]。

但由于振动的引入，振动流化床在工作过程中，要受到物料的冲击力、振动电机的高频激振力、弹簧回复力和阻尼力作用，这些周期性交变载荷使得床体的受力情况恶化，容易导致结构疲劳性损坏，缩短振动流化床使用寿命[4]。本文主要研究振动流化床在工作过程中的动态特性，分析其关键部位应力、应变分布情况及变化规律，从而避免结构共振，减小结构的应力集中，降低整体应力，提高振动流化床的可靠性。

1 振动流化床的结构及工作原理

如图1所示，振动流化床采用箱体式结构，主要由上箱体、下箱体、排料装置、激振电机和支撑装置组成。设计参数如表1所示。其中上下箱体采用锅炉钢直接焊成，并在内部布置有加强横板，上下箱体采用螺栓连接，成为一个整体式密闭箱体。四个支撑装置位置满足k1l1=k2l2[5]，其中k1、k2为弹簧刚度，l1、l2为支撑装置距质心的水平距离，即弹簧刚度距质心力矩为零。

振动流化床采用两台自同步激振电机驱动，两台电机的转速、初始相位相同，旋转方向相反，从而产生垂直于电机底座的正弦激振力，方向与水平夹角为75°。

2 振动流化床的运动学仿真

利用Pro/E5.0建立振动流化床三维模型，并导入Adams中，为减小Adams仿真时计算量，建模时将焊接固连在一起的部件做成一个零件，同时将一些对仿真结果影响不大的零件(如销钉等)加以简化，以减小Adams的仿真工作量，提高仿真效率。

在Adams中对振动流化床施加弹簧—阻尼支撑以及平面运动约束，并根据设计参数设置弹簧刚度、阻尼系数及重力方向，如图2所示。弹簧总刚度，式中z为隔振系数，取z=4，f为激振频率[6]。每个支撑装置的弹簧刚度，弹簧阻尼C取刚度值的1%。在支撑装置的水平方向施加弹簧，刚度取竖直方向刚度值的1/3，以模拟实体弹簧的横向刚度[7]。

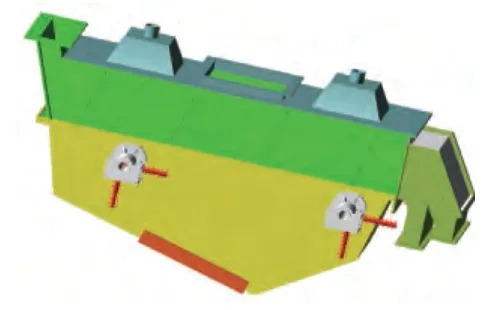
图2 振动流化床adams仿真模型

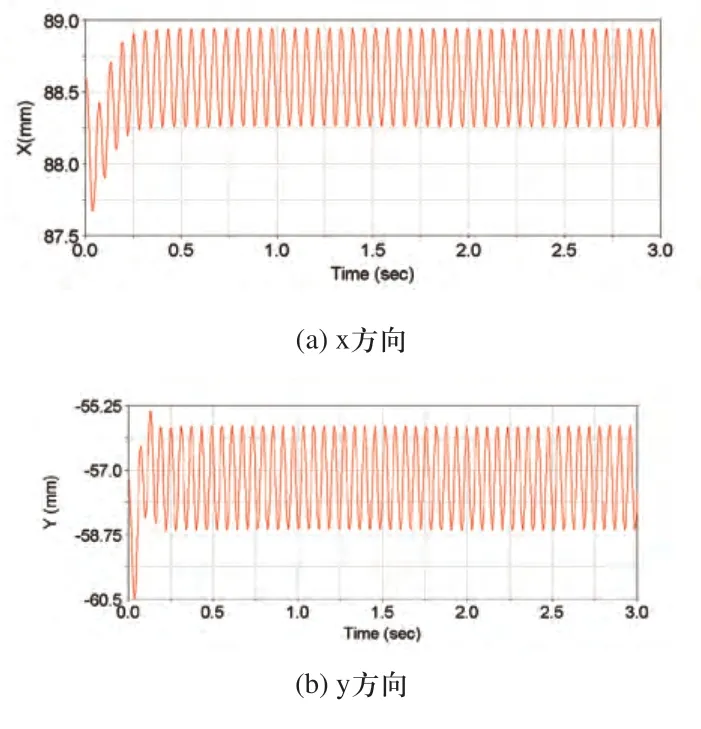
图3 振动流化床的位移－时间关系曲线

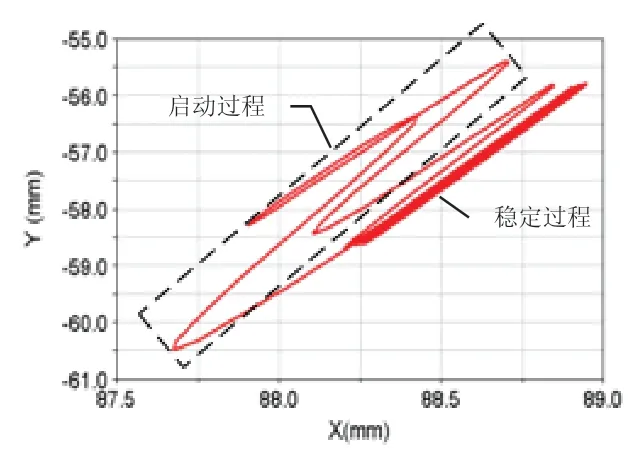
图4 振动流化床空间轨迹图

从图3、图4可以看出，在电机启动0～0.25s内，振动流化床运动较为剧烈，空间轨迹图比较紊乱，这是由于激振力瞬间施加在床体上，隔振弹簧产生大的变形造成的。在0.25s后振动流化床运动趋于平稳。正常工作状态下振动流化床位移为一平稳的正弦曲线，y方向振幅在1.41mm，x方向振幅在0.34mm，振动方向角为76.22°。运动学参数与设计要求有较好的吻合。

3 振动流化床的动力学仿真

为分析振动流化床的动态运行时的动力学特性，将Pro/E模型适当简化后转存为x_t格式，导入workbench中，进行模态分析，并在此基础上利用Adams仿真所得载荷谱进行瞬态分析。

由经典理论可知，物体的通用动力学方程为[7]：

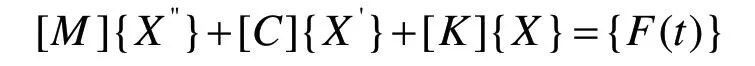
式中[M]、[C]、[K]分别是是质量矩阵、阻尼矩阵、刚度矩阵，{x''}、{x'}、{x}为对应的加速度矢量、速度矢量和位移矢量，F(t)为随时间变化的力矢量，是系统总体载荷列阵。

模态分析主要用来求解结构的固有频率和模态振型，从而使结构设计避免共振，并预测在不同载荷作用下的结构振动形式。结构的频率和振型可由动力学方程的特征方程(K-ω2M)φ=0得出，其中ω为固有频率，φ为对应的特征向量。

瞬态分析可以求解结构在随时间任意变化的载荷作用下的动力响应，从而对结构动态特性进行评估。由于动力学问题需要考虑结构的惯性，因此需要定义模型的材料属性。根据振动流化床所用材料，定义材料参数如下：E=210GPa，υ=0.3，ρ=7850kg/m3。

由于振动流化床主要存在的强度问题是箱体开裂，因此分析时忽略了布风板、连接螺栓等小质量物件以及其他对床体结构应力分布无影响或影响不大的部件；上下箱体及支撑装置与侧板之间定义Bond连接，采用接触单元TARGE170和CONTA174传递载荷，以模拟焊接及螺栓连接；由于不考虑振动电机本身的应力应变问题，将振动电机使用同质量的点质量单元代替，并布置在电机底板相应位置。支座的三个方向上施加弹簧—大地连接，并将激振力等效为施加在电机安装面上的当量均布力。网格划分前对模型进行预处理，采用自由划分法，并限制网格尺寸，以获得较好的网格划分质量。划分后的效果图如图5所示，网格划分时全部划分为 Solid187，Solid186 实体单元，共形成35923个单元,139831个节点。

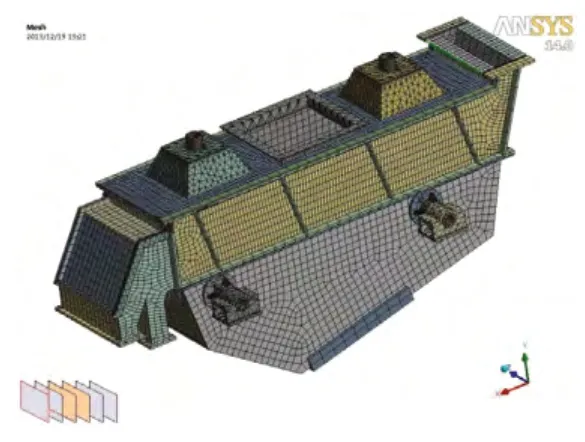
图5 振动流化床网格划分图

瞬态动力学算法有三种：直接法(Full)、缩减法(Reduced)和模态叠加法(Mode Superpos’n)。本文中采用模态叠加法求解。模态叠加法是通过对模态分析得到的振型（特征值）乘上因子并求和来计算结构响应的，为此，首先对振动流化床进行模态分析，而后在workbench的Transient分析中插入pressure，对电机底板施加激振力，点击solve进行求解。计算完成后，后处理中采用Von Mises（最大等效应力）准则对下箱体侧板进行评估，得到动态应力分布云图，如图6所示。Von Mises公式为：

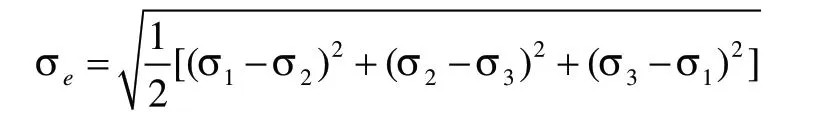
其中 σ1、σ2、σ3分别表示三个主应力，结构最大应力应小于材料的许用应力。

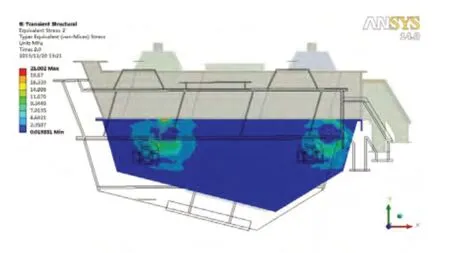
图6 振动流化床侧板动态应力分布图

根据模态分析，振动流化床前十阶固有频率如表2所示。

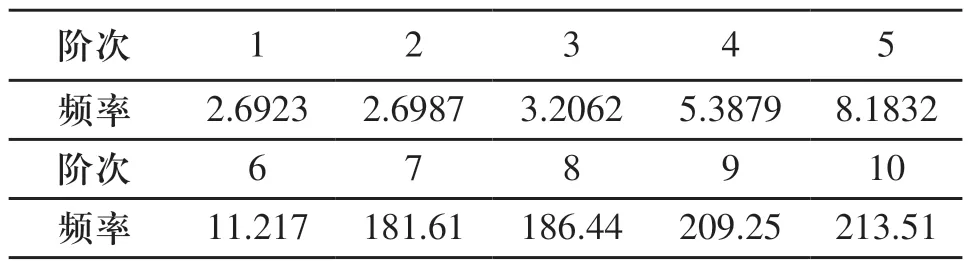
表2 振动流化床前十阶固有频率（Hz）

表2中的前六阶固有频率对应的的振型为刚体运动，由于振动流化床结构对称，所以有些固有频率数值非常相近。分析可得，振动流化床各阶频率均不与激振频率16.67Hz重合，正常工作时不会发生共振。同时由图6可以看出，最大等效应力出现在支撑装置处，最大值为21MPa，低于振动筛行业的许用应力值24.5MPa。虽然振动流化床结构满足强度要求，但由于强度储备裕量较小，在长时间周期载荷作用下仍可能发生结构破坏。为此，对振动流化床结构加以改进，即在下箱体弹簧支撑装置处增加空心圆管梁，如图7所示，利用空心圆管梁与侧板共同分担载荷，以加强结构刚度，减小侧板变形。

由于支撑装置关于振动流化床质心对称，因而增加圆管梁后未改变振动流化床水平质心，而竖直方向质心仅上升0.68mm，不会对运动平稳性造成影响。虽然增加了参振质量，但由于激振电机选型时有一定的裕量，因而不会对运动参数造成太大影响。

改进后，重新进行动态分析，结果如表3所示。

加强后振动流化床的前六阶刚体运动的固有频率略有降低，由特征方程(K-ω2M)φ=0可以看出，刚体运动频率的降低主要是是由于参振质量增加造成的。由于改进后的固有频率远离工作频率,频率裕度增加，因此有利于改善振动流化床动态性能。7～10阶固有频率较改进前有明显提高，说明圆管梁增大了结构的刚度，有利于承受外界载荷。由应力分布图图8可知，改进后的下箱体支撑装置处应力值明显降低，最大值为15.19MPa，较改进前下降了27.6%，从而验证了结构改进的合理性。

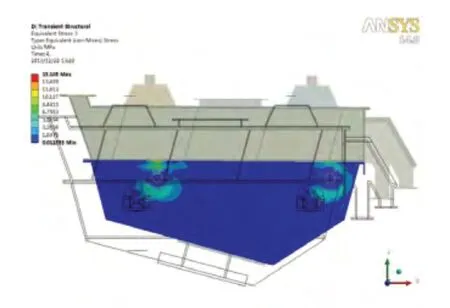
图8 加强后的振动流化床侧板应力分布图

4 结束语

1）分析表明，该型振动流化床固有频率远离工作频率，正常工作时不会发生共振造成结构损坏。

2）由于箱体式振动流化床主要存在侧板开裂问题，所以对下箱体侧板重点进行分析改进。通过增加空心圆管横梁，有效改善了振动流化床工作时的动态应力分布，降低了箱体最大应力值，有利于提高其使用寿命。

[1]朱建凤,骆振福,李振.基于物料分离的振动流化床研究现状与展望[J].煤炭工程,2007,(9):91-93.

[2]陈清如,杨玉芬.21世纪高效干法选煤技术的发展[J].中国矿业大学学报,2001,(11):527-529.

[3]李珺,刘初升,赵跃民,彭立平.新型振动流化床的动态特性及试验研究[J].煤炭学报,2013,(10):1882-1887.

[4]王建华,孔祥伟.振动流化床筛箱结构优化设计[J].机械工程师,2012,(7):108-110.

[5]张恩广.筛分破碎及脱水设备[M].北京:煤炭工业出版社,1991.

[6]王峰,王皓.筛分机械[M].北京:机械工业出版社,1998.

[7]贺孝梅,刘初升,张成勇.超静定网梁激振结构大型振动筛动态特性.煤炭学报.2008,(9):1040-1044.

[8]李范春.ANSYS Workbench设计建模与虚拟仿真[M].北京:电子工业出版社,2011.