基于支持向量机的雷达网抗干扰效能评估
袁超鹏,李 江
(1.西安电子科技大学电子工程学院,陕西西安 710071;2.中国人民解放军93861部队1大队,陕西咸阳 712000)
随着科学技术和武器装备的发展,雷达面临的作战环境越来越复杂,各种电子干扰对单基地雷达构成了严重威胁,为有效地对抗这种威胁,雷达网[1]不失为一种实现方便同时节约成本的方法。雷达网就是对多部不同频段、不同极化方式和不同体制的雷达进行适当的、合理的优化布站,对网内各部雷达的信息,进行综合处理、控制和管理,从而形成一个统一、有机、整体的雷达系统,可实现单部雷达不能实现的抗干扰能力,因此有效地评估雷达网的抗干扰能力,是雷达网部署决策中的关键问题。
雷达网抗干扰能力[2]评估是一个多目标决策问题,需考虑的因素较多,同时这些因素均存在一定程度的模糊性和不确定性。而支持向量机评估方法有严格的理论基础,同时能较好地解决小样本、非线性、高维数和局部极小值等实际问题,且具有良好的鲁棒性。因此本文通过雷达网抗干扰指标及其量值,用支持向量机理论来构建模型,并将最终结果与基于模糊物元分析法结果进行了比较,其结果表明该方法是行之有效的。
1 支持向量机(SVM)原理
支持向量机[3](Support Vector Machine,SVM)是在统计学习理论基础上发展而来的一种新型机器学习方法。其采用结构风险最小化原则代替传统统计学上的基于大样本的经验风险最小化原则,对于小样本情况下的统计学习问题有较好的学习分类能力和推广能力。基本思想是通过用内积函数定义的非线性变换将输入控件变换到一个高维空间,在这个高维空间中寻求输入变量和输出变量之间的一种非线性关系,其中可分为线性模型和非线性模型。
对于线性回归问题,给定样本集(x1,y1),…,(xl,yl),xi∈Rn为输入变量,yi∈R 为输出值,支持向量机的回归函数为

其中,wTx为内积;b∈R为阈值。
由最大间隔法[4]的基本思想,引入不敏感损失函数ε,为处理函数f在ε精度下无法处理的数据,引入变量 ξi和 ξ*i,得到用于函数逼近的支持向量机
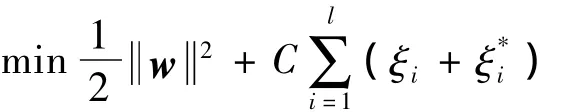

常数C为惩罚参数,控制对超出误差的样本的惩罚程度。这是一个凸二次优化问题,引入拉格朗日函数,可运用对偶原理得到以下优化问题
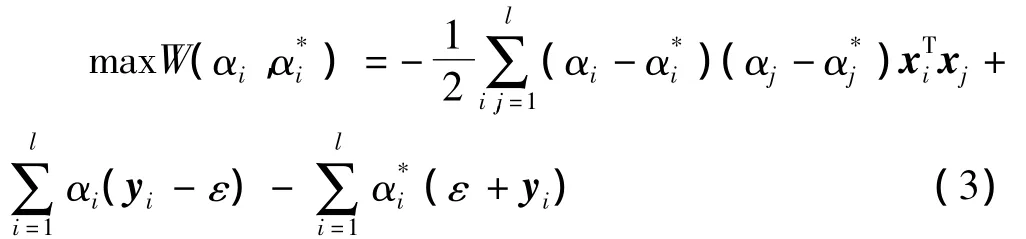
其中,αi,α*i为拉格朗日乘子,可得权向量为
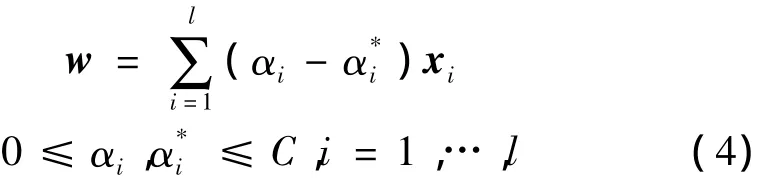
又因 αi和 α*i不可能全为0,则由 KKT(Karush-Kuhn-Tucker)条件可知
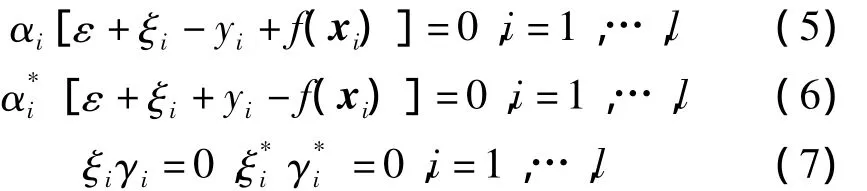
由此可见,对应于 αi=C或 α*i=C的 f(xi)与yi的误差可能 > ε;当 0< αi<C 时有 ξi=0,不等式[(w·xi)+b]- yi≤ε + ξi就变成等式,可得到 b,同样当0<α*i<C有ξ*i=0,不等式 yi-[(w·xi)+b]≤ε+ξi就变成等式,也可得到b。
在非线性逼近模型是先通过非线性变换将输入数据映射到高维空间,再在特征空间中进行线性回归,即

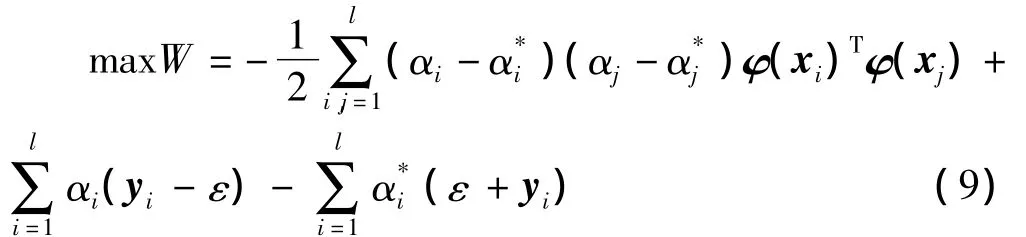
此时变为采用核函数来计算特征空间中的内积
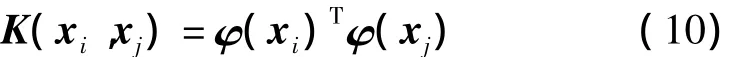
而由上式可得到非线性回归方程为
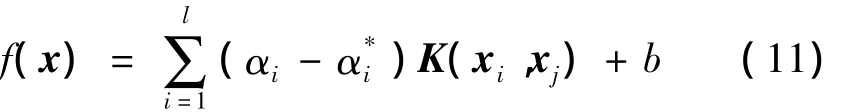
同线性类似,b可由KKT条件求出。
2 雷达网抗干扰评估指标体系
由于对雷达网抗干扰能力评估的考虑因素较多,目前没有公认的评价标准,本文对雷达网抗干扰的指标从覆盖能力和预警能力两个方面选取。所谓覆盖能力[4]是指雷达网在受干扰的情况下,能在探测责任区内对空中目标的覆盖是否连续和严密,用空域覆盖系数、频域覆盖系数和频率瞄准度来度量;所谓预测能力[5]是指雷达网在受干扰情况下发现目标的能力,可用探测时间比和跟踪时间比、航迹起始时间差来度量。组建雷达网抗干扰评价指标体系如图1所示。
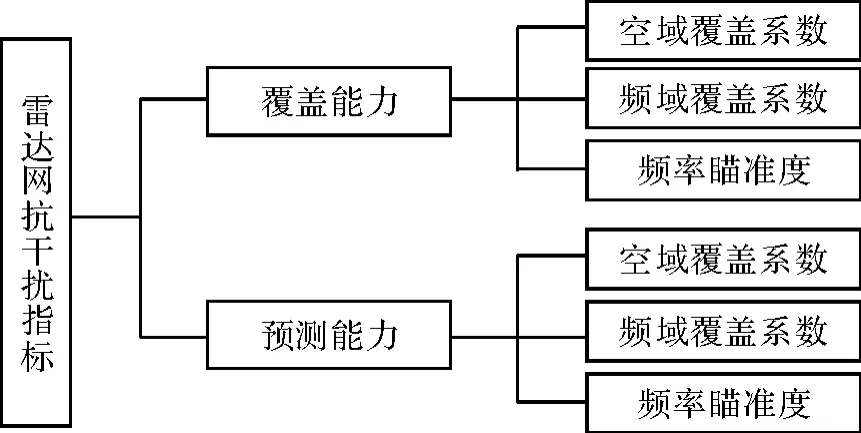
图1 雷达网抗干扰指标体系
3 仿真分析
选取10种不同的雷达组网,测量其在干扰情况下各指标相对应的指标值,并通过雷达网抗干扰能力指标值以及基于模糊物元分析法得到的评价结果值训练网络,测量值如表1所示。
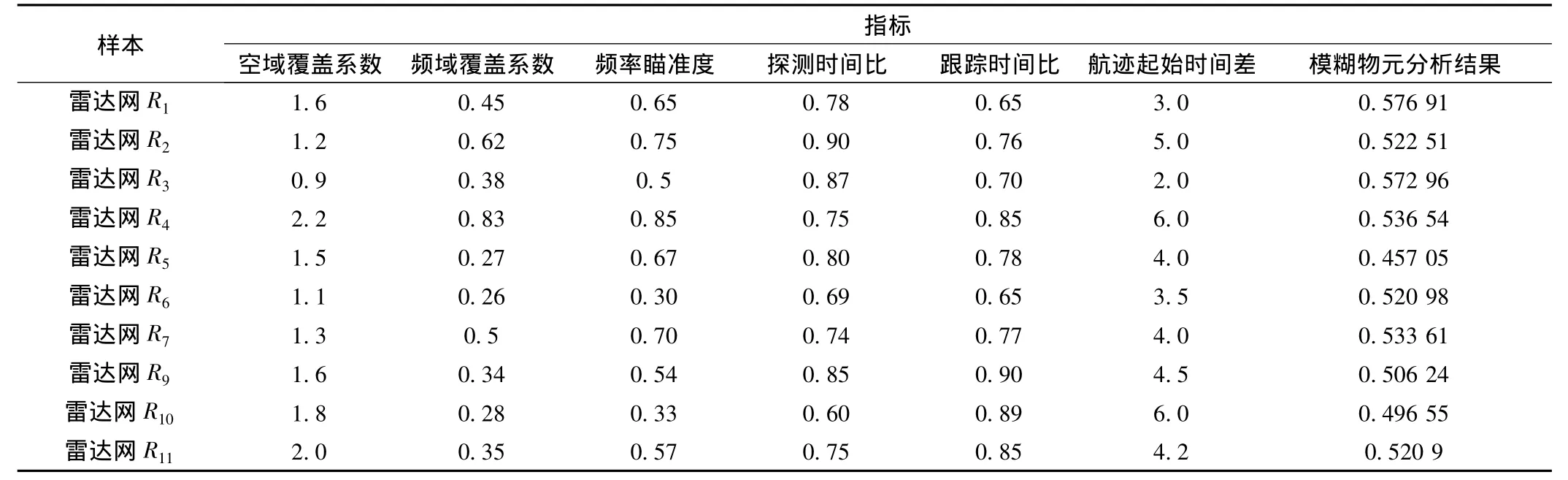
表1 10种雷达网抗干扰能力指标及模糊物元评估值
由于上表各指标具有不同的量纲,且类型不同,指标间具有不可共度性,难以进行直接比较,因此需先进行数据规范化,接着进行SVM训练。在对支持向量机训练时,主要工作是根据输入的训练样本,再依据支持向量机的回归分析法[6],为建立的模型进行参数选择。SVM的主要参数[7]包括逼近容忍误差ε、惩罚参数C。参数C用于控制模型复杂度和逼近误差的折衷,每个数据子空间至少存在一个合适的C使得SVM推广能力最佳,通常确定其范围为1~1 000;损失函数的参数ε通过控制回归逼近误差管道的大小,从而达到控制支持向量的个数和泛化能力的目的,其值越大,精度越低,则支持向量越小。为了在拟合精度和泛化能力之间平衡,ε的取值范围一般为0.000 1~0.01。
文中选择前6个样本作为训练样本,进行SVM训练,此处核函数选择径向基函数,经反复验证,当容忍误差ε为0.00 1,惩罚参数C为100时,训练结果较好,如图2所示。
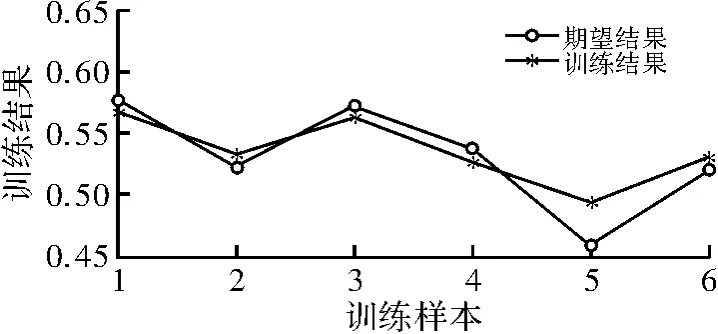
图2 训练结果与期望结果对比图
在图2中,通过参数选择,当容忍误差ε为0.001,惩罚参数C为100时,训练结果和期望结果具有较好的拟合度,此时得到的训练网络较为满意。
利用训练好的网络对检测样本,即后4种样本进行预测,预测结果如图3所示。预测结果和模糊物元分析法给出的期望结果相对误差如图4所示。
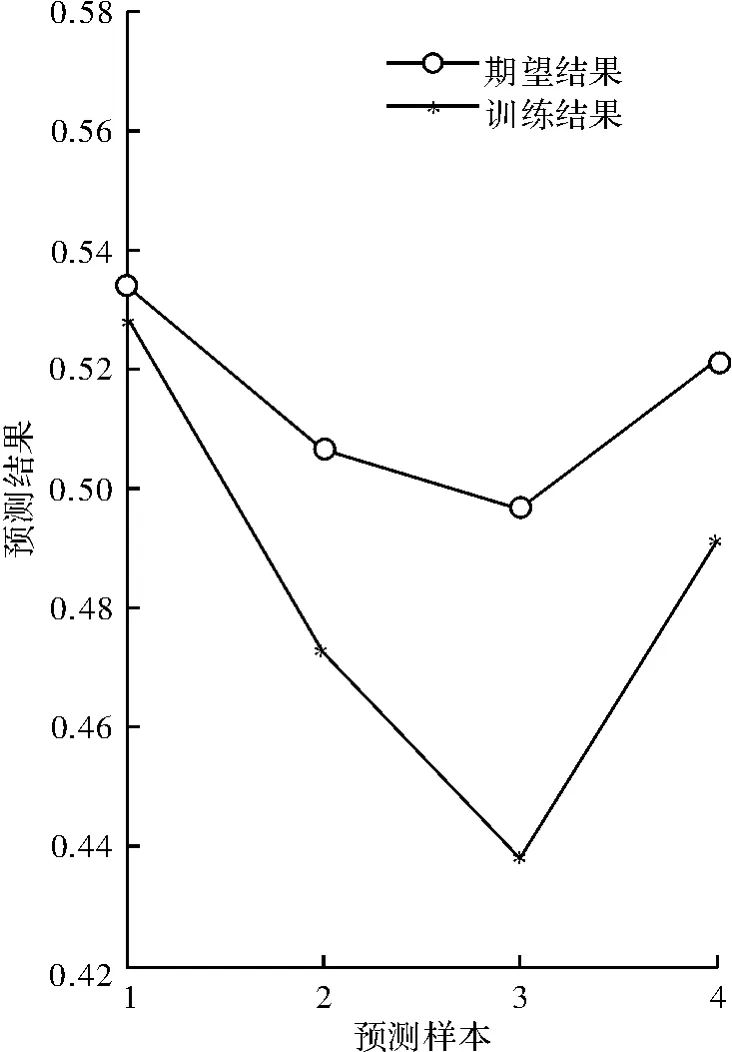
图3 预测结果及期望结果对比图
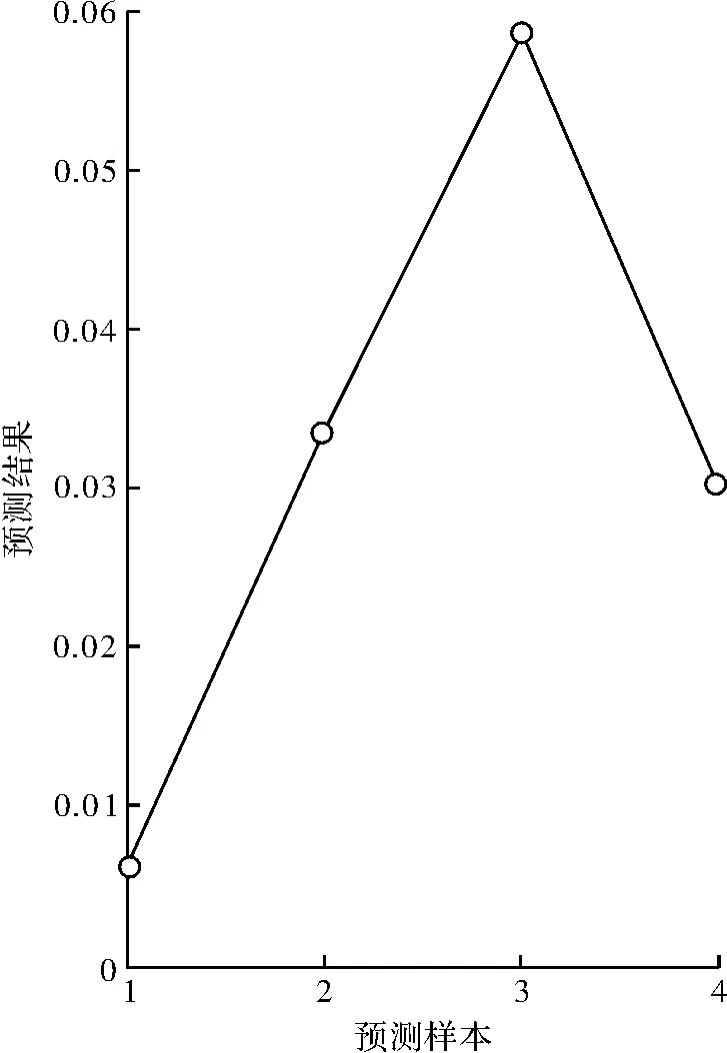
图4 预测结果和期望结果相对误差
在图3中,期望结果为模糊物元分析法结果,预测结果为预测样本经SVM训练后的训练结果。从图中可看出,期望结果和预测结果有些许偏差,其相对误差如图4所示,误差最大值为0.06,最小值为0.005,其误差对评估结果影响较小。雷达网抗干扰能力大小关系并无本质变化,即雷达网R7>雷达网R10>雷达网R9>雷达网R8,其评估结果的大小关系与基于模糊物元分析法的相同,表明基于支持向量机的评估方法行之有效。
4 结束语
雷达网抗干扰能力评估需考虑的因素众多,针对具体给定的信息,在评估方法的选取上应注重实效性。文中提出基于支持向量机的评估方法,理论可靠,同时能较好地解决小样本、非线性、高维数和局部极小值等实际问题,且具有良好地鲁棒性。
[1]尹以新,何明浩,马晓岩.雷达组网ECCM性能评估方法[J].系统工程与电子技术,2000,22(11):53 -54.
[2]张培峰,赵拥军,时银水.雷达网抗干扰效能评估方法研究[J].现代电子技术,2008(7):29-30.
[3]白鹏,张喜斌,张斌,等.支持向量机理论及工程应用实例[M].西安:西安电子科技大学出版社,2008.
[4]CHEN Zhigang,LIAN Xiangjiao.Fault diagnosis for valves of compressors based on support vector machine[C].Chinese Control and Decision Conference,2010:1235 -1238.
[5]李乗,王凤山,李炜.基于模糊物元分析法的雷达网抗干扰能力评价[J].现代防御技术,2009,6(3):110 -111.
[6]罗鹏程,杨涛.对空警戒雷达网抗干扰效能模型[J].火力与指挥控制,2010,35(7):58 -59.
[7]陈果,周伽.小样本数据的支持向量机回归模型参数及预测区间研究[J].计量学报,2008,1(29):93-96.
[8]廖睿,唐灿华.基于支持向量机的作战方案评估[J].电脑知识与技术,2012,16(10):2446 -2448.

