一种实现LED均匀圆斑照明透镜的自由曲面设计
张成亮
(合肥工业大学电子科学与应用物理学院,安徽合肥 230009)
发光二极管(Light Emitting Diode,LED)是一种新型的绿色光源,与传统光源相比,具有节能、高效、环保、性能稳定、体积小、寿命长等优点。近年来,随着半导体芯片技术及封装技术的发展,LED的发光效率得到不断提高。2012年丰田合成在“第四届新一代照明技术展”上公开了170 lm/W的白色LED的产品化得以实现。在国内LED的发光效率最高也可达到142 lm/W,远高于白炽灯。LED光源的光强分布为通常为朗伯型[1],若直接用于照明,在目标面上将呈现为中心强边缘弱的圆形光斑,难以达到实际使用要求,这就需要对LED进行2次配光[2]。由于LED的尺寸小,一般的芯片大小为1 mm×1 mm,所以在进行配光时将LED视为点光源。可以采用自由曲面透镜设计的方法使LED发出的光均匀地分布在照射面上,目前常用的自由曲面设计方法[3]主要有微分方程法、划分网格法、参数优化法以及同步多曲面方法SMS(Simultaneous Multiple Surface)。参数优化法主要依赖设计人员的经验,最终结果是经过反复多次优化得到的,因此不可避免地要花费较长时间。SMS方法主要是针对扩展光源而言的,微分方程法和划分网格法是现有方法中较为有效的两种方法,两者都有各自的优点。偏微分方程法获得的自由曲面面型数据是通过求解偏微分方程得到的,无需采用试错法,目的性较强,且计算速度快,可在短时间内得到自由曲面的面型数据,该方法要求设计人员具有较强的数学基础以和熟练的编程能力;划分网格法是根据能量守恒原理,利用光源到照明面所需光分布的映射,这种方法可以解决复杂的照度分布问题,通过网格的细化来提高精确度,无需进行误差校验。本文将采用微分方程法对LED二次配光的透镜自由曲面进行设计。
1 LED的光源特性分析
LED光源的发光特性类似朗伯型,配光曲线可以用下面的表达式来描述

式中,φ是LED的发光方向和LED晶片平面法向之间的夹角;I0是LED法线方向的发光强度值。参数m由半角值 φ1/2决定,有光束角的定义,当 φ=φ1/2时,有I(φ)=I0/2,求解式(1)可得

当m=1(φ1/2=60°)时,LED即可被视为理想朗伯体,此时LED的配光曲线为

LED发出的总光通量为

其中,φmax是LED出射光线的最大出射角,一般为90°。
2 自由曲面的构造与求解
以光源所在位置为原点建立直角坐标系,如图1所示。这里透镜的内表面是以坐标原点为球心的球面,光线经过内表面时不改变方向,因此只需设计外表面即可。这里先考虑二维情况,以透镜所在的xz切面为例。
Snell折反射定律的矢量形式可表示成
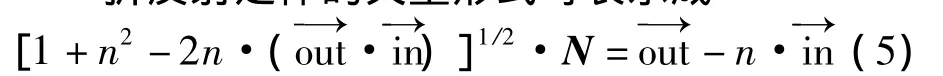
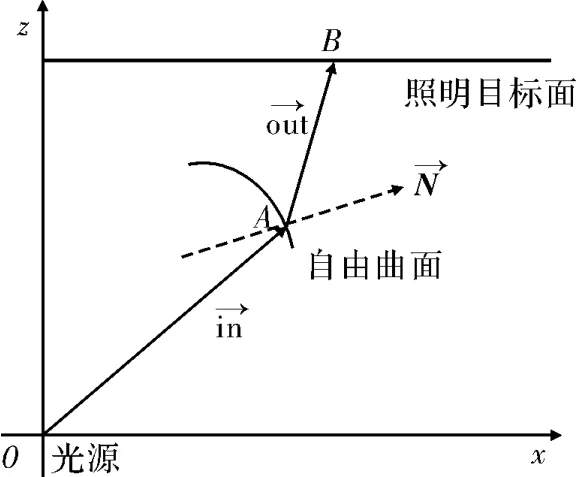
图1 光源、透镜的自由平面以及照明面在xz平面示意图

其中,d x和d z分别是自由曲面分量在x和z方向的微分;H是光源到目标面之间的垂直距离。
将式(6)代入式(5)可得

其中
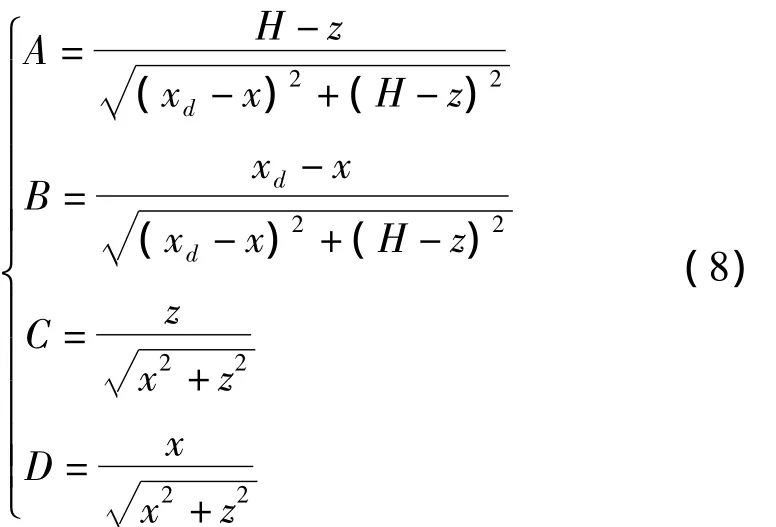
为求解方程d z/d x=f(x,z,xd)还需附加一个条件xd=g(x,z),由于是均匀照明故可设照度为定值E,照明目标面的照射面积为S。因此,出射光线照到目标面上的总光通量为

如果不考虑能量的损耗,光线传播满足能量守恒定律,光源发出的能量等于照明面接受的能量

圆形照明区域的半径为R,则面积为

由式(4)、式(9)~式(11)可得
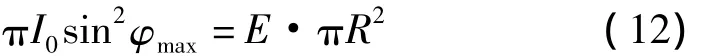
光源与z轴夹角φ内的所有光线经过透镜后都照射到照明面上半径为xd的圆形区域内,有能量守恒定律可得
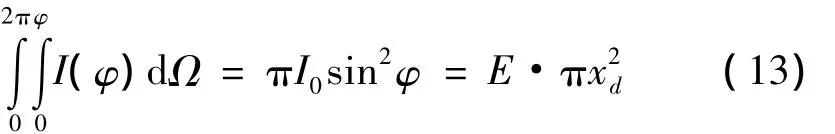
由式(12)和式(13)可得

即
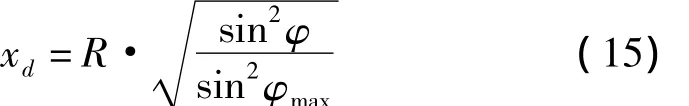
其中
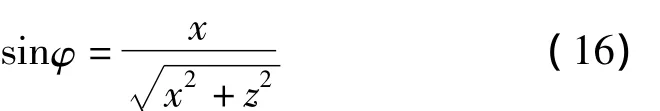
将式(15)~式(16)、式(8)代入式(7)进行化简便可得到 dz/dx关于 x和 z的显式表达式 dz/dx=f(x,z)。由于f(x,z)的表达式比较复杂,直接求解方程的解析表达式很困难,这里采用数值方法[4]进行求解。
在这里将采用四阶Runge-kutta方法[5]来求解该方程。四阶经典Runge-kutta格式为

其中,h为迭代步长。
设自由曲面与z轴相交于点(0,0,z0),经过计算可得到自由曲面在xz平面的部分曲线,将得到的曲线绕z轴旋转一周就能得到完整的自由曲面。
3 仿真与验证
设置光源到目标照明面的距离为H=300 mm,照明半径为R=500 mm,初始条件z0=5 mm。利用四阶Runge-kutta方法并采用Matlab编程就可得到自由曲面在xz平面的曲线上点的坐标。将Matlab编程得到的坐标数据保存以扩展名为.ibl的文件,用记事本程序打开,并在第一行前加入如下代码[6]:
open
arclength
begin section
begin curve
关闭记事本程序并保存。打开Pro/E,新建实体,单击“插入曲线”,选择“自文件”,然后选择坐标系,选择上述生成的.ibl文件,即可完成数据导入Pro/E拟合成一条曲线,再绕z轴进行旋转即可得到自由曲面的透镜模型,如图2所示。
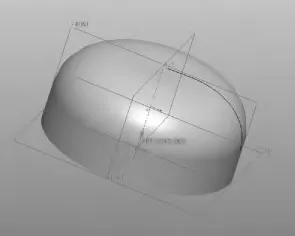
图2 用Pro/E建立的透镜模型
最后进行验证,将此模型导入Tracepro,并设置好光源、透镜材料、接受面等,选择PMMA为透镜材料(折射率为1.493 5),光源用朗伯型1 mm×1 mm×1 mm的小立方体代替,这里设置1 200 000条光线进行追迹便可得到照度分布图,如图3所示,光强曲线分布如图4和图5所示。
从生成的数据和图中可得到产生了半径为500 mm的圆形照明区域,光通量/发射光通量为87.261 lm,光能利用率为87.261%,照度均匀度>90%。实验结果如图所示,边缘部分光照强度减小是因计算时将光源近似为点光源,但仿真时将光源设置为一个1 mm×1 mm×1 mm的小立方体,透镜折射率按1.5计算,但仿真时所选材料的折射率为1.493 5,同时计算时假设点光源发出的所有光线都能通过自由曲面照射到照明区域,但实际上与LED晶片平面的法线夹角为90°附近的发射光线是较难通过透镜照射到目标照明区的[7-9]。可以在仿真时将光源尺寸设置得越小越好,步长h设置尽可能小,同时在计算时可将透镜折射率设置为1.493 5,从而可以得到更精确的自由曲面透镜。
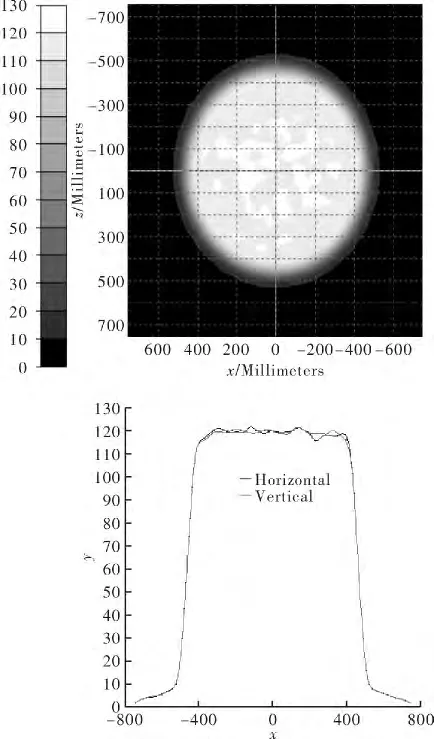
图3 照度分布图
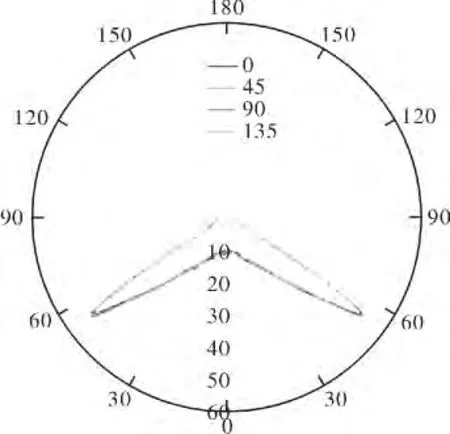
图4 极坐标Candela分布图
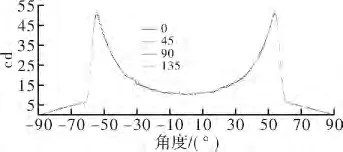
图5 矩形Candela分布图
4 结束语
通过Snell折反射定律和能量守恒定理建立了偏微分方程d z/d x=f(x,z),利用四阶Runge-kutta方法并采用Matlab编程,最终得到了透镜在xz平面的曲线坐标值,借助Pro/E可以得到所设计的自由曲面透镜,最后用Tracepro对所设计的透镜进行了模拟验证,用实例仿真实现了LED在目标平面的均匀照明,通过此方法可以快速有效地给LED配光。
[1]李小彤.几何光学和光学设计[M].杭州:浙江大学出版社,1997.
[2]深圳雷曼光电科技股份有限公司.简论LED二次光学设计[J].现代显示,2010,4(11):38 -39.
[3]WANG L,QIAN K Y,LUO Y.Discontinuous free - form lens design for prescribed irradiance[J].Applied Optics,2007,46(18):3716-3723.
[4]苏煜城,吴启光.偏微分方程数值解法[M].北京:气象出版社,1989.
[5]王能超.计算方法——算法设计及其Matlab实现[M].2版.武汉:华中科技大学出版社,2010.
[6]胡赤兵,姚洪辉,肖根先,等.基于Matlab及PRO/E的全参数化齿轮设计[J].新技术新工艺,2010(2):30-32.
[7]金永镐,金杰.微功耗高灵敏度声光控制型LED照明灯的设计[J].电子科技,2012,25(3):66-68.
[8]杨毅,钱可元,罗毅.一种新型的基于非成像光学的LED均匀照明系统[J].光学技术,2007,33(1):110 -112,115.
[9]王洪,王海宏,张小凡,等.旋转轴对称LED均匀照明系统设计方法[J].光电子·激光,2010,21(8):1163 -1166.

