多类指派约束下汽车总装装配线平衡优化

殷旅江，何 波，杨立君

（1.湖北汽车工业学院 经济管理学院，十堰 442000；2.华中科技大学 机械学院，武汉 430000）

0 引言

流水装配线生产组织方式将零部件按照产品装配的工艺顺序，以规定生产节拍，连续地、有节奏地依次经过每一个工作站进行装配，直到变为成品离开[1]。在这个过程中要解决的一个最基本的问题是装配线平衡问题，它直接影响生产效率和制造资源的利用率[2]。而在实际装配线平衡问题上，随着装配线规模的扩大，装配线中作业元素的增多，以及各种约束的限制，装配线的优化过程越来越复杂，装配线的平衡状况和利用效率并不令人满意，许多装配线经过进一步的平衡可使生产效率提高10%以上[3]。由于装配线不平衡存在效率低下、成本浪费的现象，因此装配线平衡技术在中国企业有很大的市场研究意义。

1 汽车装配线问题

某汽车集团公司以生产长安面包车和轻型客货两用车为主，某总装车间的装配流水线全长50m，原有35个工序，设18个工位，25名装配工，生产节拍约300秒，工位平均充实度低于80%[4]。

根据该汽车实际装配线的操作步骤，其中的部分测试结果如表1所示。

在该装配线中，由于工具、特殊操作等原因，作业6必须在工作站编号3上操作，作业26必须在工作站4上操作，作业30必须在工作站5上操作。由于工艺与加工的工具要求必须分配到同一个工作站作业编号有14与15，6与7，20与21。不能分配到同一个工作站的作业有作业4与9，作业2与6，作业30与31。

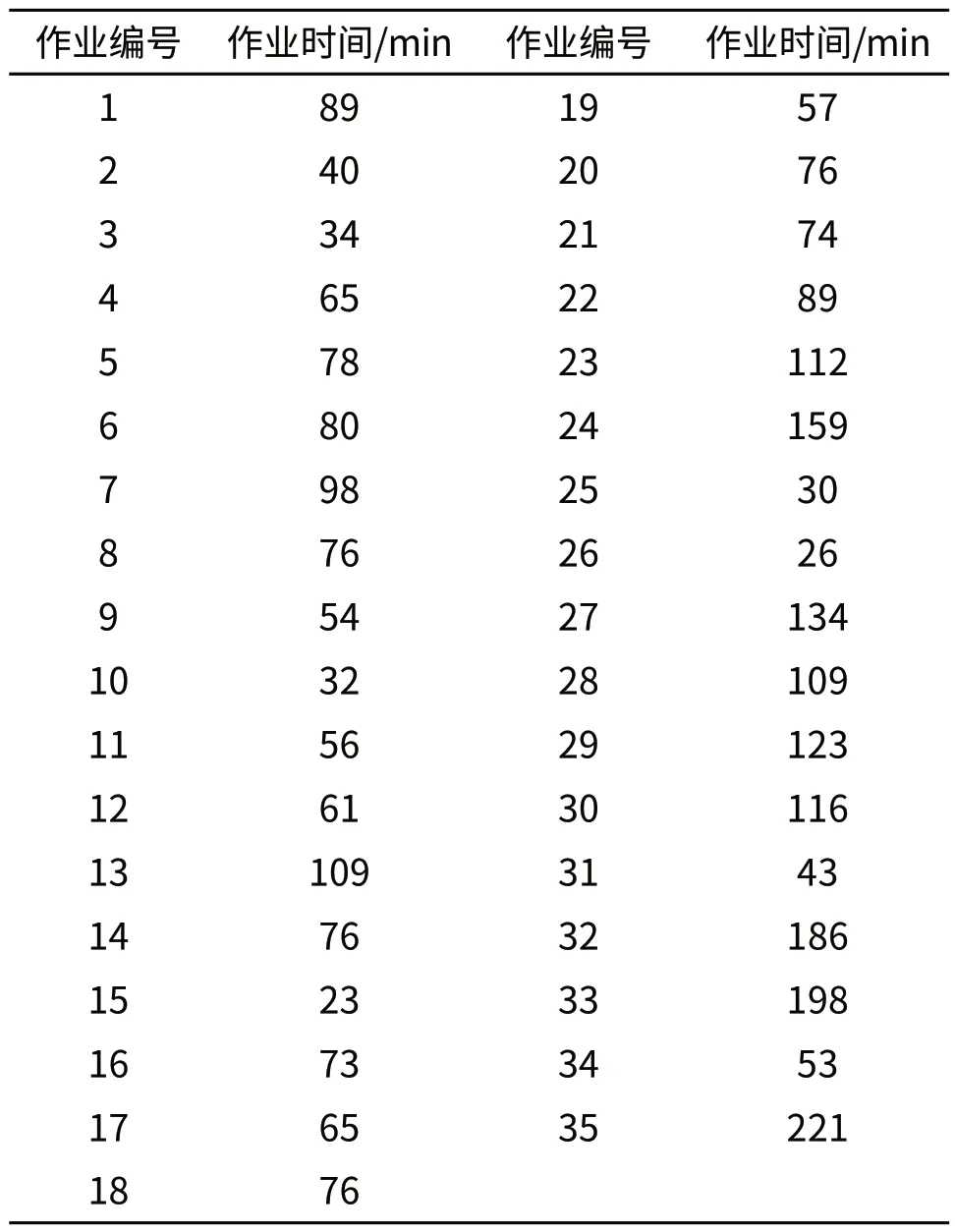
表1 装配线作业表

该汽车装配线中的紧前工序和紧后工序用作业有限顺序图表示。如图1所示：圆圈表示各个操作，序号代表作业编号，箭头表示先后顺序。

图1 作业先后顺序图

2 多类指派约束建模

2.1 装配线平衡

装配线平衡根据其求解目标不同，可分为两类子问题：第一类装配线平衡问题是给定生产节拍，最小化工作站数；第二类问题是给定工作站数，最小化生产节拍[5]。本文是使用第二类装配线平衡优化方法进行装配线优化。

第二类装配线平衡问题优化是在满足各种工艺约束，如工时约束、工艺顺序约束、设备约束和位置约束，同时保证工作站的数量不变的情况下，将所有装配作业单元组合分配到装配线的工作站上，使得工作站的节拍最小，加快产品在装配线中流动速度，最终达到降低装配线生产单件产品的作业时间，提高整个装配线效率的目的[6]。

2.2 模型变量定义

在建模之前，对模型中所用到的数学变量进行定义，其定义如下：

变量I：装配线中所有作业单元的集合(I={1,2,…,i,…,m})。

变量K：装配线中所有工作站的集合(K={1,2,…,k,…,n})。

变量ti：作业单元i的作业时间，i ∈I。Sk：工作站k的额定工时，k ∈K。

变量Xik：表示作业单元i和装配工作站k的关系：Xik=1当作业单元i分配在工作站k上；Xik=0当作业单元i分配不在工作站k上。

变量Ak：工作站上是否有作业单元：Ak=1工作站k上有指派作业；Ak=0工作站k上没有指派作业。

变量C：在装配线中流水线的工作节拍，即产品在一个工作站上进行操作的最长时间。

针对第二类装配线平衡问题目标函数为最小工作站节拍：minz=C。

2.3 约束条件

在该生产线平衡中，我们主要考虑了发生约束、工作站时间约束、优先权约束、相容约束、相斥约束、空间约束、独立性约束和位置约束这八大约束。其中约束条件及数学描述如表2所示[7]。

表2 八大约束条件

2.4 线性规划模型

当工作站数目确定以后，根据已知的约束条件，建立线性规划模型，具体模型如下：

目标函数为：minz=C

约束条件为：

3 模型求解及结果分析

3.1 模型求解

本文模型求解过程是通过LINGO软件编程实现，在多次实验模拟下，确定在工作站设定为13。主代码如下：

3.2 结果处理

在确定工作站数目为13情况下，对每个工作站的作业元素进行统计，得到各个工作站中被分配到的作业，求得最小工作站节拍为243秒，将每一个工作站的作业元素的作业时间求和，得到各个工作站在优化后的工作时间。每个作业被分配到的工作站如表3所示，汽车装配线经过优化之后各个工作站的饱和度如表4所示。

各工作站的工作效率如图2所示。

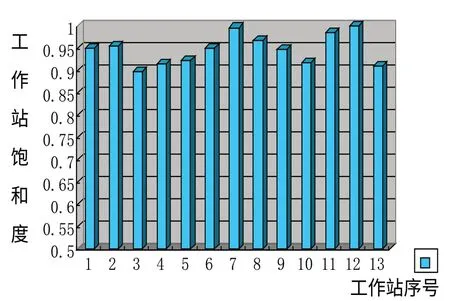
图2 工作站效率直方图

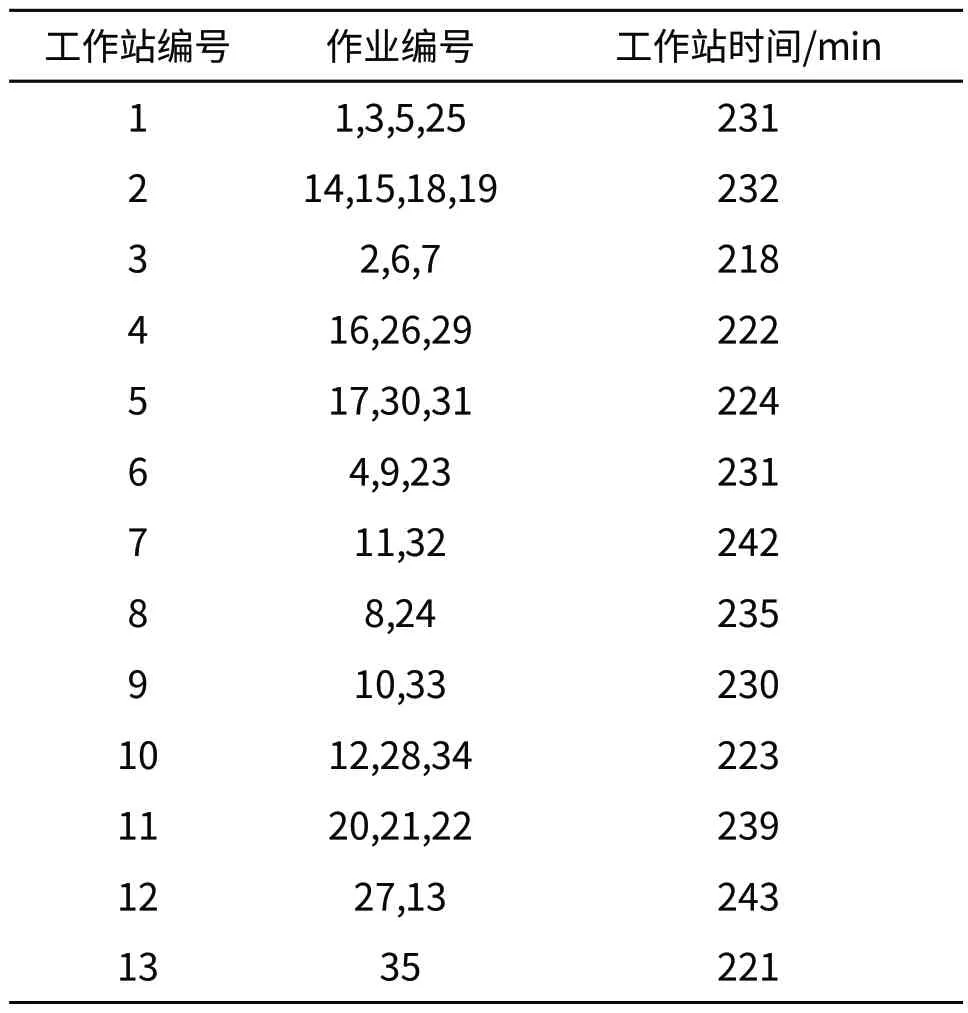
表3 工作站的作业元素

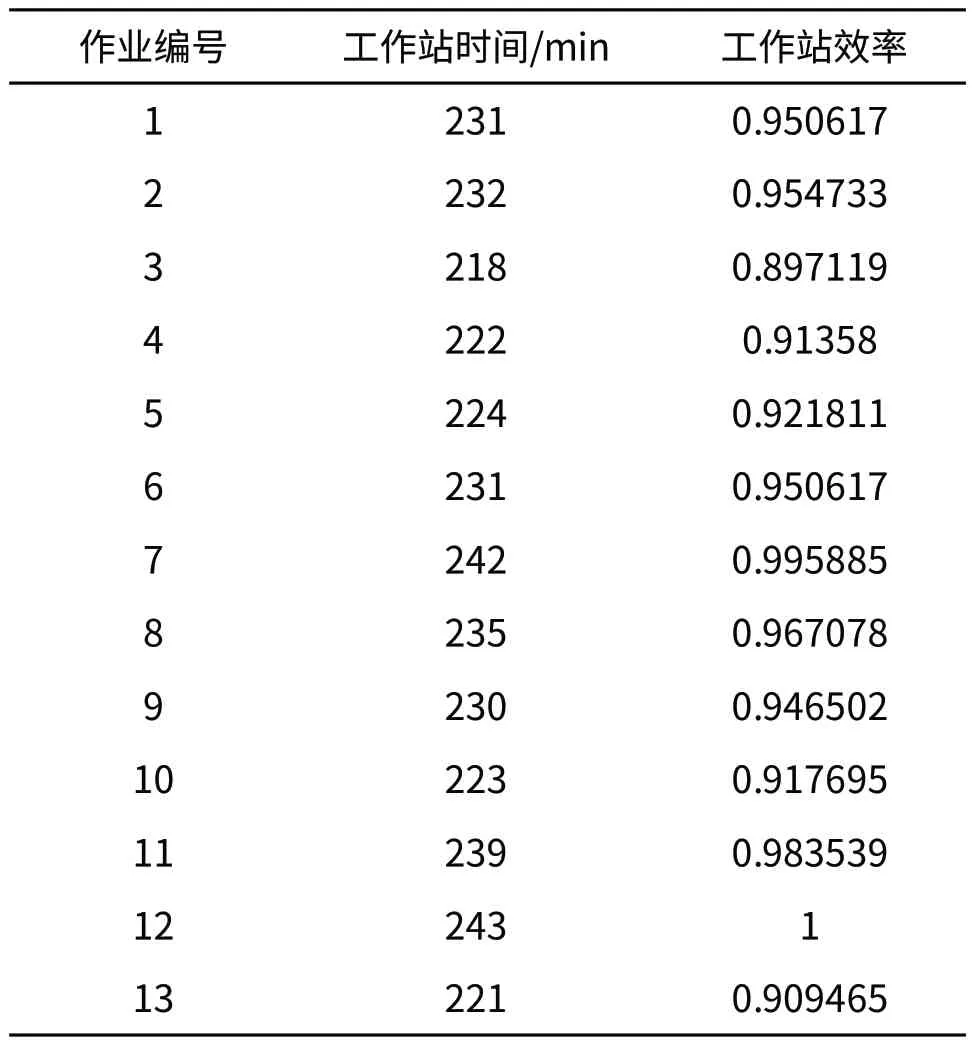
表4 优化后的工作站作业情况

工作站平均的饱和度为：

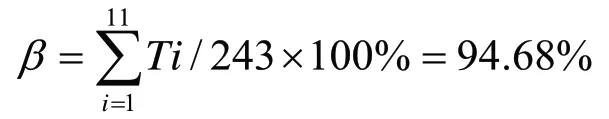
计算该装配线的时间损失指数：

3.3 结果评价

表5 装配线优劣结果评价标准

通过对优化后的结果分析可知：优化后工作站的个数为13个，工作站节拍为243秒，平均每个工作站的工作站的饱和度为94.68%，装配线的时间损失指数为5.323%，按规定为一条较合理的装配线。比起优化之前18个工作站，工作节拍为300秒，工作站的平均充实效率低于80%，在减少工作站的同时，减少了该装配线上的工作站数量，装配线的工作效率显著提高。

4 结束语

本文主要结合某汽车装配线，考虑实元素之间诸多的约束条件，利用第二类生产线平衡问题的解决方法，建立优化模型，最后运用LINGO软件进行运算得到优化结果，对优化结果进行评价，提高了装配线的利用率约15%，使装配线中各个工作站的作业量更加平衡，大大节约了企业建设与运营成本。

另外，由于线性规划模型存在一定的局限性，本文只探讨了装配线平衡在满足一定条件下，单一目标函数取得最优解的情况。在未来的研究中，将会结合合适的方法来弥补线性规划问题的局限性，求解多目标规划的装配线平衡问题。

[1]杜运普,杨月新.装配生产线的平衡问题研究[J].机械设计与制造,2003,02:104 -106.

[2]苏平,于兆勤.混流装配线平衡问题的多目标优化方法研究[J].中国机械工程,2009,19:78-82.

[3]陈心德.生产运营管理[M].清华人学出版社,2005.

[4]耿双华.基于工业工程的解放卡车装配线改善的研究[D].天津大学,2009,5.

[5]宋华明,韩玉启.多目标装配线平衡的优化算法[J].运筹与管理,2002(11):56-62.

[6]吴隆,余海明,吴媛媛.基于LINGO汽车装配线平衡与研究[J].工业工程与管理,2008,6:74-107.

[7]查靓,徐学军.多类约束下U型装配线平衡建模研究[J].工业工程与管理,2011,2:59-63.