基于工序成本的集成协作计划与调度模型研究

杨雨露，任晓青，邱 婉，包振强，王伟业

（扬州大学 信息工程学院，扬州 225127）

0 引言

传统递阶结构的制造资源计划（MRP）分解方法将计划与调度分为两个阶段，在确定零件各生产周期的生产批量时，由于没有考虑具体的调度约束，计划与调度不能够有效的衔接，通常导致制定的计划在调度中不可行[1]，影响了调度的动态适应性和决策的有效性[2]。目前，对于将计划与调度两者集成的问题，国内外不少学者已经有了较为深入的研究，然而其中大部分文献重在解决单资源单目标车间调度问题[3～7]，即以生产周期为优化目标，以加工设备为资源约束，且工艺路线固定的车间调度问题。但是，实际作业车间中，工件通常有多条不同的加工路线，当车间自身加工能力不足时，不管怎样调度都不能在规定工期内完成相应的计划，必须采取外包的方式。也就是说工件的调度除了受加工设备这一种资源约束外，还受其自身加工能力以及合作伙伴的约束[8]。针对以上问题，本文建立了一个基于工序成本的集成协作计划与调度模型，既能确定最佳的工艺路线，又能确定工序的成本和总成本。并用改进的遗传算法求解该模型，给出了成本最低的最佳调度，在保证计划完成的前提下实现了调度的同步。

1 基于工序成本的集成协作计划与调度模型

本文所建模型为：作业车间有多种工件需要加工，同一种工件有多条不同的工艺加工路线可选，同一个工件不同的工序有严格的先后顺序，并且作业车间自身的加工能力不足。要求制定一个能同时满足一下要求的生产计划：1）能为各个工件选择合适的工艺加工路线；2）能在尽可能短的生产周期内完成加工任务；3）能根据工序成本和外包所需的协作成本给出总成本最低的最佳调度集合。

本文所用符号与变量定义如下：定义H为很大的正数；N为待加工任务的个数；n为不可外包的工件数；TZ为工件的生产周期；Z为完工工期；Tihjk为工件i在选择工艺加工路线为h后其工序j在第k台设备上的完工时间；调度后的工件加工数量用P表示。此外，调度约束中的符号定义如下：若工件i选择工艺加工路线为h后的工序j在工件p选择工艺加工路线为q后的工序s前被加工，且k设备既能加工j也能加工p，则Yihjpqsk=1，否则Yihjpqsk=0；若工件i选择工艺加工路线h，则Xih=1，否则Xih=0。

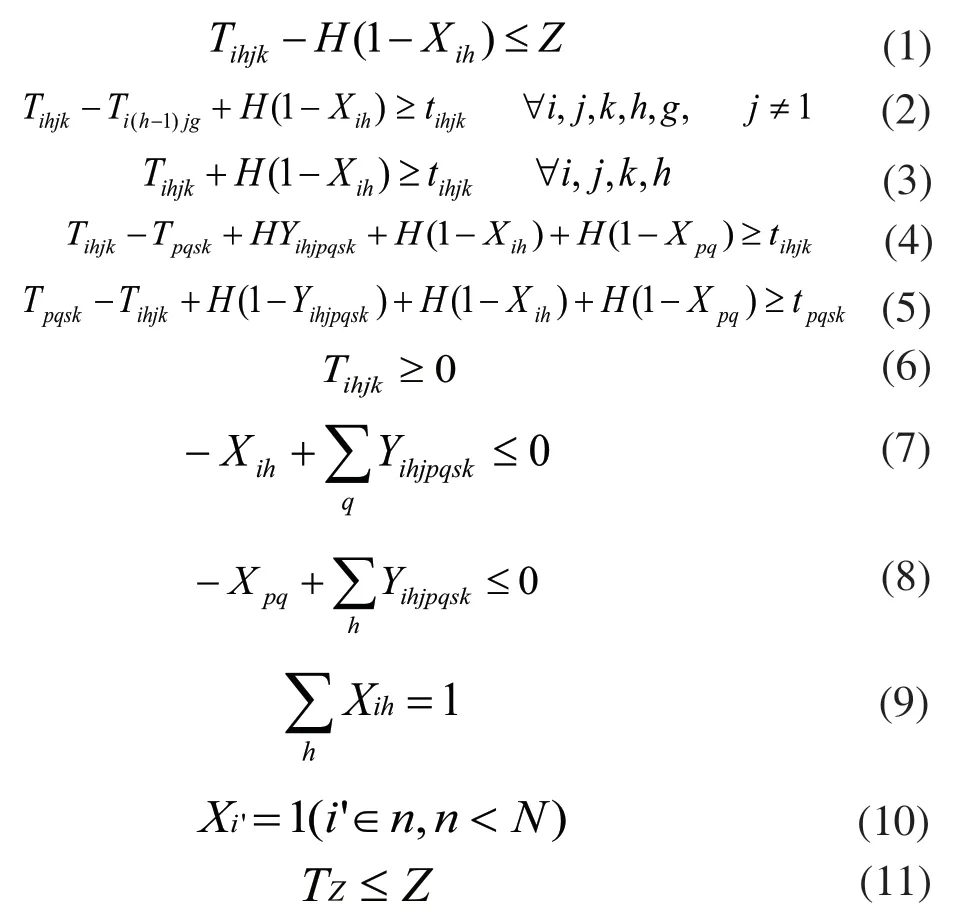
其中，当工件i的工艺加工路线满足式(1)和式(9)时，最后一道工序的完工时刻所对应的调度目标为Maximize P（Minimize Tz）；式(2)和式(3)表示对于工件i的两个连续的工序，若在不同的设备上加工，则i的前一道工序必须在后一道工序前加工；式(4)表示在同一台加工设备k上，选择了第q条加工路线后的Ops（Ops表示工件p的第s道工序）比选择了第h条加工路线后的Oij先加工完；式(5)表示的加工顺序与式(4)相反，但二者同时保证了同一台设备在同一时刻不能加工多道工序；式(7)和式(8)保证任一工件在选择了一条工艺加工路线后都具备上述先后顺序；式(9)表示只能从各工件的多道工艺加工路线中选择一条；式(10)表示N个待加工任务中有n个无法外包给合作伙伴。

2 算法设计

本文通过对遗传算法[9～11,14]进行改进来解决求解本文所建的基于工序成本的集成协作计划与调度模型。采用的启发式规则[12,13]是优先选择最短加工时间的工序（Shortest Processing Time first，SPT），它被证实是求解生产周期和平均流动时间的最佳规则。

2.1 染色体表现型

针对所建立的存在柔性路径的模型，本文采用基于工序的染色体编码方案。给相同工件的不同工序标注同一符号，他们在染色体中的顺序即为工序的顺序，如表1所示。同时，由于考虑了协作，本文在设计染色体编码时附加了一段基于工件编码的协作染色体，如表2所示，用1表示外包，0表示自行加工。

染色体的初始种群为随机产生。

表2 附加染色体编码方式

2.2 选择算子

本文采用赌轮机制优先选择适应度值高的个体进行遗传操作。种群P 的规模为N，本文适应度函数如式(12)：

其中Cmax表示种群中成本最大值，Cmin表示种群中成本最小值，C(Li)表示所求染色体对应的成本。ε是为了避免适应值为0而给的一个小小的补偿。此外，若经过调度排序后染色体的生产周期超出规定的生产周期，则规定其适应值为一个很小的值。

2.3 交叉算子

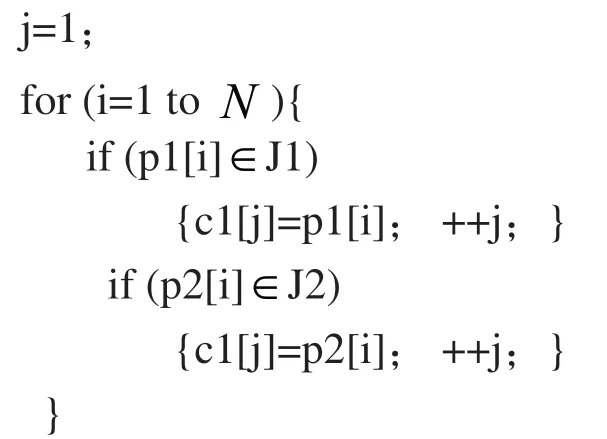
程序运行后得到一个新染色体c1，交换p1和p2再执行一次以上程序得到另一个染色体c2。最后从这四条染色体中选择适应值大的两个进入下一步操作。

2.4 变异算子

本文的变异方法为随机交换所选染色体中任意两个基因位上的基因，如图1所示。

表1 主染色体编码方式

图1 变异操作

3 算例及仿真

本文所设算法参数如下：种群规模N=50，迭代次数T=50。

本文的实验仿真数据如下：有6台加工设备，9种工件，其中每个工件有3道不同的工序。表3的加工信息表给出了各零件在不同的可加工设备上的加工时间；表4的工件成本表给出了各零件的变动成本以及各自的协作成本；表5的工序成本表给出了各工序在不同的可加工设备上的加工成本。

表3 加工信息表

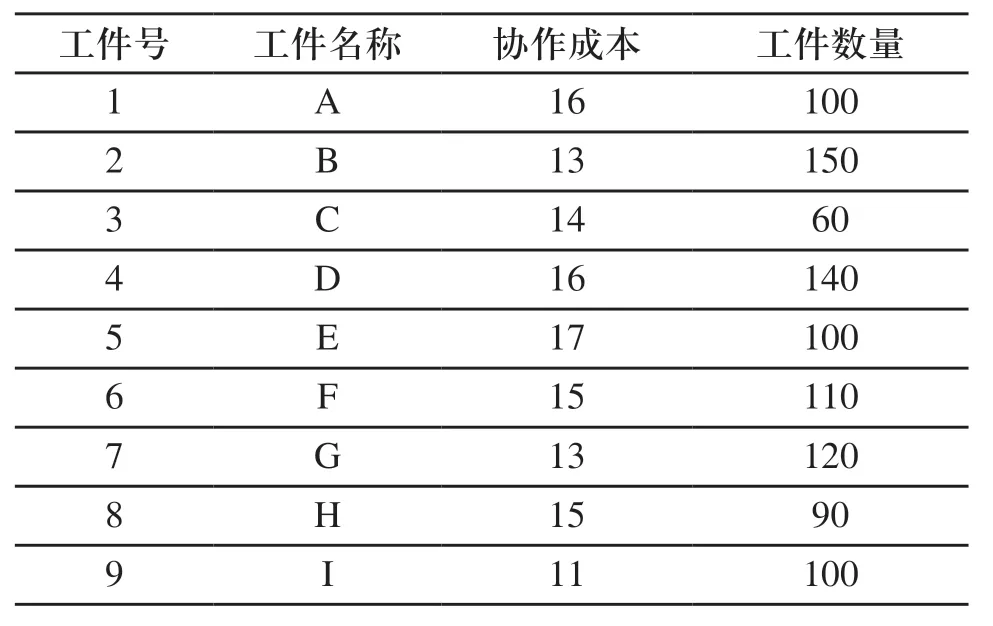
表4 工件成本表

表5 工序成本表

上述算例经实验后得到一组解集，从中可知，自行加工的最小生产周期为35，也就是说，若交货期大于35，则该车间可自行加工完成，但若交货期小于35，无论怎么调度，都无法在规定时间内完成任务，必须将部分工件外包给协作伙伴完成。图2～图4分别给出了完工周期为38，29和24所对应的甘特图。由图可知：周期为38的调度任务全部自行完成；周期为29时，由于自身能力的约束不能完全自行加工，将工件4、5、9外包给了协作伙伴；周期为24时将工件1、3、4、9外包给了协作伙伴。由此可见，外包给协作伙伴的工件数量越多，则对应的完工周期越短。但外包数量并不是越多越好，图5（其中横坐标表示完工周期，纵坐标表示对应的总成本）给出了完工周期和总成本之间的关系，分析该图我们可知完工周期越短，总成本越大。因此决策者必须根据个人偏好和实际情况来进行决策，以便选出最适合的调度排序。

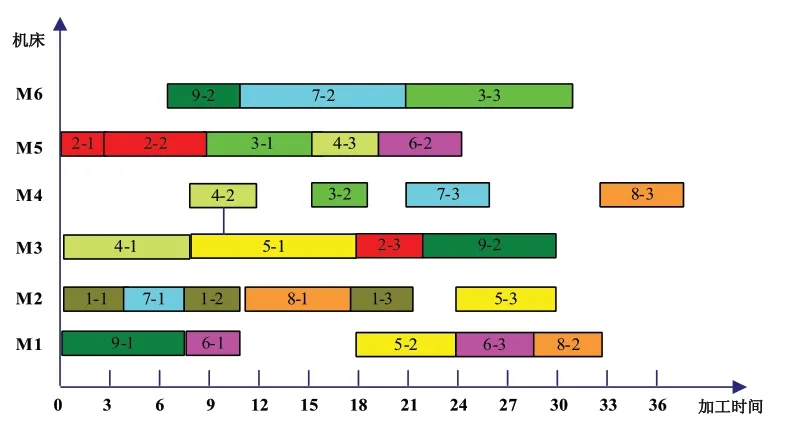
图2 无协作甘特图

图3 有协作甘特图（周期29）

图4 有协作甘特图（周期24）

4 结束语

本文提出了一个基于工序成本的集成协作计划与调度模型，解决了传统递阶结构的制造资源计划分解方法将计划与调度分为两个阶段，使计划与调度不能够有效的衔接的问题。同时，有效地统一了计划、调度、工艺路线决策与协作生产。该模型有效地解决了制造企业加工能力不足的问题，更好的实现了企业内部生产调度的及时性和企业外部协作生产快速适应性。

图5 完工周期和总成本关系

[1]刘胜辉,王丽红.求解车间作业调度问题的混合遗传算法[J].计算机工程与应用,2008,44(29)：73-75.

[2]尚文利,范玉顺.成批生产计划调度的集成建模与优化[J].计算机集成制造系统,2005,11(12)：1663-1667.

[3]鞠全勇.智能制造系统生产计划与车间调度的研究[D].江苏：南京航空航天大学,2007.

[4]Rajkumar M,Asokan P.A GRASP algorithm for the integration of process planning and scheduling in a flexible job-shop[J].International Journal of Manufacturing Research.2010,5(2)：230-251.

[5]Seyed Habib A,Rahmati M,Zandieh M.Yazdani.Developing two multi-objective evolutionary algorithms for the multi-objective flexible job shop scheduling problem[J].The International Journal of Advanced Manufacturing Technology,2013,64(5-8)：915-932.

[6]李峥峰.多时间因素作业车间调度问题的研究与工程应用[D].湖北：华中科技大学,2010.

[7]An Yu-Wei,Yan Hong-Sen.Solution strategy of integrated optimization of production planning and scheduling in a flexible job-shop[J].Zidonghua Xuebao/Acta Automatica Sinica,2013,39(9)：1476-1491.

[8]王洪锋,李洪宇.生产计划和车间排程问题的整数规划解法[J].现代制造工程,2008,7：92-95.

[9]葛继科,邱玉辉,吴春明,蒲国林.遗传算法研究综述[J].计算机应用研究,2008,25(10)：2911-2916.

[10]Li Jian-hong.An improved GA for job-shop scheduling problem[J].Advanced Materials Research.2013,630：486-489.

[11]Zhao Zi-xiang.Job-shop scheduling optimization design based on an improved GA[C].// Proceedings of the World Congress on Intelligent Control and Automation.United States：Institute of Electrical and Electronics Engineers Inc.,2012：654-659.

[12]温蕴,孙亚.基于启发式规则和蚁群算法的车间作业调度方法[J].计算机应用与软件,2009,26(6)：187-188,194.

[13]Wang Jiaxin.Heuristic rule for scheduling[J].Qinghua Daxue Xuebao/Journal of Tsinghua University(Science and Technology),1995,35(5)：27-32.

[14]Chien C-F,Chen C-H.Using genetic algorithms (GA)and a coloured timed Petri net (CTPN) for modeling the optimization-based schedule generator of a generic production scheduling system[J].International Journal of Production Research.2007,45(8)：1763-1789.