更新模型在缺少大震离逝时间的活动断裂强震发生概率计算中的应用研究
郭 星 潘 华
1)中国北京100081中国地震局地球物理研究所
2)中国北京100082环境保护部核与辐射安全中心
引言
在实际地震危险性分析中对于地震发生过程的描述,最常用且数学上最为简单的模型即泊松过程模型(Cornell,1968).该模型假定在一个断层或一个震源区内,地震的发生符合泊松过程.泊松过程的特点是时间上的无记忆性,即未来发生地震的可能性与上一次地震的离逝时间无关,这与已知的强震发生的弹性回跳理论不一致.依据弹性回跳理论(Reid,1910),一次大地震发生以后,必须积累足够的能量才能够在同一地点发生下一次大地震.因此,若积累速率保持恒定,则距离上一次地震的时间越长,下一次地震发生的可能性就越大,此即大地震发生的时间记忆性.显然,泊松模型不能反映这一特点.
为了描述大地震的记忆性,Utsu(1972)和Rikitake(1974)以及 Hagiwara(1974)基于弹性回跳理论提出一种更新模型,该模型假定地震的发生符合更新过程,即大地震的发生具有时间相关性,一次大地震发生后,还需要很长时间的弹性应力能量的积累才能在同一断层段上发生下一次地震.
为了描述未来一段时期ΔT内发生潜在地震的可能性大小,国外研究人员提出很多用来计算这种条件概率的更新概率模型,包括双指数分布(Utsu,1972)、高斯分布(Rikitake,1974)、对数正态分布(Nishenko,Buland,1987)、威布尔分布、伽马分布(Utsu,1984)和BPT分布(Ellsworth,1999;Matthews et al,2002)等.
对于任一更新概率模型,若强震发生的概率密度分布函数f(t)和前一次地震的离逝时间T已知,就可以计算分段断层源上未来一段时期ΔT内强震发生的条件概率(Wesnousky,1986):

然而,由于强震重复周期较长,而有强震记载的历史较短,很多断层源(或分段断层源)上并没有上一次强震发生的时间,这种情况下很难使用更新模型估计强震的发生概率.然而很多断层源上已经有数百年甚至上千年的有确切记载的强震平静期,若采用泊松过程模型则可能会低估强震发生的危险性.
针对缺少大震资料情况下活动断裂上强震发生概率的计算,Matthews等(2002)对于给定的时间界限(已知或认为地震发生在这个时间点之前),给出了一个描述该时刻处于不同加载状态的稳态(steady-state)概率密度函数,然后利用全概率公式和BPT(Brownian passage time)概率密度函数计算得到未来一段时期ΔT内的发震概率.但该方法仅适用于基于一种随机加载过程(稳定加载附加布朗运动)的BPT模型.
本文对更新模型的条件概率计算方法进行了改进,提出一种以有确切记载的强震平静期长度Ts为参数的条件概率计算方法.这里Ts要小于上一次地震的离逝时间T,而T是不确定的.本文提出的方法具有通用性,可以用于各种更新概率模型.
本文以东昆仑断裂带东段的塔藏段为研究对象,分别利用泊松分布模型与BPT分布模型计算该段的强震发生概率,并给出有确切记载的强震平静期长度Ts与强震发生概率P的对应关系.
1 方法
若无法确定断层源上前一次大地震的离逝时间T,但是如果已知研究区内强震记载完整的初始年份及其距今的时间Ts,根据贝叶斯公式,则可利用强震发生的概率密度分布函数f(t)推断断层源上未来一段时期ΔT内发生强震的条件概率P(Ts,ΔT).
首先令至今至少存在长度为Ts的平静期的事件为BTs,而现在的大震离逝时间为T的事件为AT;再以T年前时刻发生大震的事件为ET,其下一次地震将在未来时段发生的事件为X.根据上述定义,则有

若当今之前的历史地震情况未知(无历史大震和平静期资料,即是无记忆的),根据等可能决策法(或拉普拉斯决策法),则可认为这个未知期内每一年发生地震事件(ET)的概率相同,即P(ET)为常数,这里设该常数为ν;若已知大震发生的概率密度分布函数f(t),则在T年前发生大震(ET)条件下,其下一次地震将在未来时段发生(X)的条件概率为

根据贝叶斯公式,在下一次地震将在未来时段发生(X)的条件下,该大震在T年前时刻发生的条件概率P(ET|X)为

式中,P(ET)为先验概率,P(ET|X)为后验概率,∫∞0(1-∫T0f(t)dt)dT则相当于一个常数.式(2)中,P(ET|X)即为大震离逝时间为T 的概率P(AT).
令P(BTs|AT)表示在大震离逝时间为T(AT)条件下,当前至少存在长度为Ts的平静期事件(BTs)的概率.其表达式为
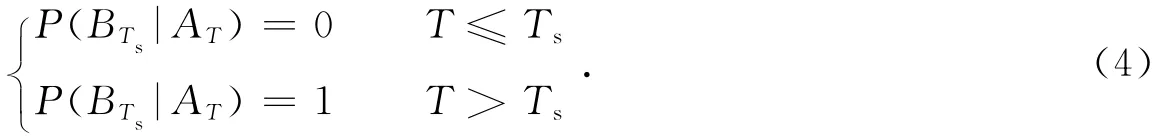
然后利用贝叶斯公式即可计算至今至少存在长度为Ts平静期(BTs)的条件下,大震离逝时间为T(AT)的条件概率P(AT|BTs)为

式中,P(AT)为先验概率,P(AT|BTs)为后验概率.若P(AT|BTs)已知,利用全概率公式,则断层源上未来一段时期ΔT内发生强震的条件概率为

2 算例
为验证本文方法的有效性,利用该方法计算了东昆仑断裂带东部塔藏段的强震发生概率.塔藏断裂位于东昆仑断裂带东段(图1),属于“玛曲空区”范围(付俊东等,2012).该断裂缺乏历史强震数据,区域GPS数据结果显示该区域可能处于应变积累阶段(任金卫,王敏,2005).

图1 东昆仑断裂带东段的几何结构及塔藏段位置示意图(引自李正芳等,2012)Fig.1 The geometrical structure schematic diagram of the eastern segment of East Kunlun fault and the location of Tazang segment(after Li et al,2012)
塔藏断裂位于岷山强断隆与甘南强隆区之间的边界带上,为一条全新世活动断裂,断裂长度60km,平均水平左旋滑动速率为2.7—2.8mm/a(李正芳等,2012).
东昆仑断裂带东部的塔藏段属于分段明确的断层源,本研究假定其符合Aki(1984)以及Schwartz和Coppersmith(1984)提出的特征地震模型.特征地震模型中最关键的就是对平均特征震级和平均复发周期这两个参数的估计.
2.1 平均特征震级和平均复发周期的估计
对于东昆仑断裂带东部塔藏段的平均特征震级,本文采用Wells和Coppersmith(1994)给出的走滑型地震的震级MW-破裂长度L的经验关系式来估计,即

由式(7)计算得到塔藏段的平均特征震级¯MW为7.2.
利用更新模型计算强震的发生概率,需要给出特征地震的平均复发间隔,也叫重复周期.由于塔藏段缺少古地震数据和大震的同震位错数据,本文采用地震矩释放率法估计其特征地震的重复周期(Youngs,Coppersmith,1985).
若已知活动断裂带的分段和各段的滑动速率,则其平均复发间隔为

式中:¯M0为地震矩,可由特征地震的平均震级¯MW确定;˙M0为地震矩释放率,由断裂段平均滑动速率、断裂段长度、断裂面宽度、地震比例因子等确定.其中地震比例因子是指发生特征地震的滑动占总滑动的比例.参照加州概率工作组和美国地震区划图,本文取地震比例因子为0.9(Frankel et al,2002;Working Group on California Earthquake Probabilities,2003).
震级为MW的地震所释放的地震矩M0可由Hanks和Kanamori(1979)给出的矩震级-地震矩的经验关系式计算得到,即

式中地震矩M0的单位为dyn·cm,而本文中地震矩的单位采用的是N·m,在计算过程中需要进行单位换算.对于断层上年平均地震矩释放率的估计,一般利用平均滑动速率S与断层发震面积A的关系式计算得到,即

式中:μ为地壳岩石的剪切模量,本文中μ取3.3×1010N/m2;L和W 分别为发震断层的长度和下倾宽度.
当没有足够的资料来确定断层的下倾宽度时,可以采用Wells和Coppersmith(1994)给出的走滑断层下倾宽度与震级之间的关系式来估计,即

将塔藏段的平均特征震级7.2代入式(11)中得到走滑断层下倾宽度W 为15km;再根据式(10)计算得到塔藏段的年平均地震矩释放率˙M0=8.3×1016N·m/a,去掉10%的蠕滑分量,结果为˙M0=7.5×1016N·m/a;最后将˙M0和¯M0代入式(8)计算得到塔藏段特征地震的平均重复周期为1 059年.
2.2 概率模型
本文所选取的更新模型为比较常用的BPT模型(Ellsworth,1999;Matthews et al,2002).利用BPT模型计算出塔藏段未来50年的强震发生概率,并与泊松模型的计算结果进行比较.
泊松模型的概率密度函数为f(t)=λexp-(λt),而未来ΔT年内强震发生的概率为P=1-exp(-λΔT).在泊松分布下,地震复发的条件概率与离逝时间无关,其未来年内地震ΔT年发生率是不变的,等于平均复发间隔τ的倒数(1/τ).
BPT模型的概率密度函数为
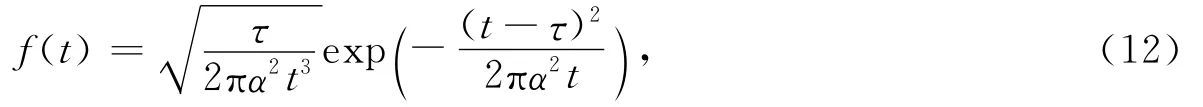
式中,τ为断裂段的平均复发间隔,α为平均复发间隔的变异系数.
Ellsworth等(1999)在分析了37个地震序列后发现,α=0.5可作为活动构造所有不同震级的地震序列复发间隔变异系数的估计值,因此建议α可直接取0.5.Working Group on California Earthquake Probabilities(2003)的研究结果也表明,尽管在实际计算时采用了对3个不同α的计算结果进行加权平均的方式,即α(权值)为0.3(0.2),0.5(0.5),0.7(0.3),但实际上α取0.5也能恰当地反映出复发间隔的变异性.综合上述分析,本文中α值取0.5.
2.3 计算结果
已知BPT模型的概率密度函数f(t)和特征地震的平均重复周期τ,即可利用式(1)计算得到塔藏段不同离逝时间T所对应的未来50年强震发生的条件概率(图2).利用式(6)则可计算得到塔藏段不同记载完整的平静期长度Ts所对应的未来50年强震发生的条件概率(图3).

图2 塔藏段离逝时间T与未来50年强震发生概率的关系Fig.2 The relation between the length of time(T)since last earthquake and the occurrence probability(P)of large earthquakes for a 50-year exposure period on the Tazang fault segment

图3 塔藏段上平静期长度Ts与未来50年强震发生概率的关系Fig.3 The relation between the length of time(Ts)with historical record of quiet and the occurrence probability(P)of large earthquakes for a 50-year exposure period on the Tazang fault segment
本文同时还给出了利用泊松模型计算得到的条件概率.通过两种类型的比较可知,只有当Ts与τ的比值非常小时,由式(6)计算得到的条件概率才接近于泊松分布;而当Ts接近于2倍的τ时,条件概率达到最大,之后开始下降.因此,若研究区内有较长时间的有确切记载的平静期,则利用泊松模型估计强震发生概率可能会低估强震发生的危险性.
鉴于本文目的仅在于方法性探讨,因此仅粗略地估计了研究区域M≥7.0地震资料基本完整的起始年.参考中国大陆分区地震资料基本完整的起始年分布图像(黄玮琼等,1994),确定塔藏段M≥7.0强震资料基本完整的起始年为1561年.
已知研究区内M≥7.0强震资料完整的起始年为1561年,即研究区内距今已有452年的有确切记载的大震平静期,因此可利用式(6)计算得到塔藏段未来50年强震发生的条件概率为P(452,50)=0.064 9,而利用泊松模型计算得到的条件概率则为0.046 1,其小于更新模型计算得到的结果.
3 讨论与结论
本文在更新模型的基础上,提出一种基于有确切记载的大震平静期Ts的条件概率计算方法.该方法解决了更新模型无法在没有历史大震记载断层上使用的不足,为强震发生概率的计算提供了一种新的选择.
从本文的计算结果可以看出,只有当Ts非常小时,即有确切记载的大震平静期长度较短的情况下,使用泊松模型才不会低估活动断裂的强震发生概率.
我国有着悠久的地震史料记载,针对这些历史地震资料,特别是强震资料完整性的研究,对于强震发生概率的估计具有重要意义.
本研究旨在提出一种新的发震概率计算方法,部分震源参数的计算过程比较简单.因此,本文给出的塔藏段未来50年强震发生概率仅供参考,要获得更精确的计算结果,尚需进行更深入的工作.
付俊东,任金卫,张军龙,熊仁伟,杨攀新,陈长云,胡朝忠.2012.东昆仑断裂带东段塔藏断裂晚第四纪古地震研究[J].第四纪研究,32(3):473-483.
Fu J D,Ren J W,Zhang J L,Xiong R W,Yang P X,Chen C Y,Hu C Z.2012.Research on Late Quaternary paleoearthquake on Tazang fault on the eastern section of the Kunlun active fault[J].Quaternary Sciences,32(3):473-483(in Chinese).
黄玮琼,李文香,曹学锋.1994.中国大陆地震资料完整性研究之二:分区地震资料基本完整的起始年分布图像[J].地震学报,16(4):423-432.
Huang W Q,Li W X,Cao X F.1994.Research on completeness of earthquake data on the Chinese mainland(Ⅱ):The regional distribution of the beginning years of basically complete earthquake data[J].Acta Seismologica Sinica,16(4):423-432(in Chinese).
李正芳,周本刚,冉洪流.2012.运用古地震数据评价东昆仑断裂带东段未来百年的强震危险性[J].地球物理学报,55(9):3051-3065.
Li Z F,Zhou B G,Ran H L.2012.Strong earthquake risk assessment of eastern segment on the East Kunlun fault in the next 100years based on paleo-earthquake data[J].Chinese Journal of Geophysics,55(9):3051-3065(in Chinese).
任金卫,王敏.2005.GPS观测的2001年昆仑山口西MS8.1级地震地壳变形[J].第四纪研究,25(1):34-44.
Ren J W,Wang M.2005.GPS measured crustal deformation of the MS8.1Kunlun earthquake on November 14th 2001in Qinghai-Xizang Plateau[J].Quaternary Sciences,25(1):34-44(in Chinese).
Aki K.1984.Asperities,barriers,characteristic earthquakes and strong motion prediction[J].J Geophys Res,89(B7):5867-5892.
Cornell C A.1968.Engineering seismic risk analysis[J].Bull Seismol Soc Am,58:1583-1606.
Ellsworth W L,Matthews M V,Nadeau R M,Nishenko S P,Reasenberg P A,Simpson R W.1999.A Physically-Based Earthquake Recurrence Model for Estimation of Long-Term Earthquake Probabilities[R].Washington:U S Geological Survey:99-522.
Frankel A D,Petersen M D,Mueller C S,Haller K M,Wheeler R L,Leyendecker E V,Wesson R L,Harmsen S C,Cramer C H,Perkins D M,Rukstales K S.2002.Documentation for the 2002 Update of the National Seismic Hazard Maps.Open-File Report 02-420[R].Washington:U S Geological Survey:2-31.
Hagiwara.1974.Probability of earthquake recurrence as obtained from a Weibel distribution analysis of crustal strain[J].Tectonophysics,23:313-336.
Hanks T C,Kanamori H.1979.A moment-magnitude scale[J].J Geophys Res,84(B5):2348-2350.
Matthews M V,Ellsworth W L,Reasenberg P A.2002.A Brownian model for recurrent earthquakes[J].Bull Seismol Soc Am,92(6):2233-2250.
Nishenko S P,Buland R A.1987.A genetic recurrence interval distribution for earthquake forecasting[J].Bull Seismol Soc Am,77(4):1382-1399.
Reid H F.1910.TheMechanicsoftheEarthquake,The California Earthquake of April 18,1906[R].Washington:State Investigation Commission,Carnegie Institution of Washington,(2):43-47.
Rikitake T.1974.Probability of an earthquake occurrence as estimated from crustal strain[J].Tectonophysics,23(3):299-312.
Schwartz D P,Coppersmith K J.1984.Fault behavior and characteristic earthquakes:Examples from the Wasatch and San Andreas fault zones[J].J Geophys Res,89(B7):5681-5698.
Utsu T.1972.Large Earthquakes Near Hokkaido and the Expectancy of the Occurrence of a Large Earthquake of Nemuro[R].Coordinating Committee for Earthquake Prediction,7:7-13.
Utsu T.1984.Estimation of parameters for recurrence models of earthquakes[J].Bull Earthq Res Inst,Univ Tokyo,59:53-66.
Wells D L,Coppersmith K J.1994.New empirical relationships among magnitude,rupture length,rupture width,rupture area,and surface displacement[J].Bull Seismol Soc Am,84:974-1002.
Wesnousky S G.1986.Earthquake quaternary faults,and seismic hazard in California[J].J Geophys Res,91(B12):12587-12631.
Working Group on California Earthquake Probabilities.2003.Earthquake Probabilities in the San Francisco Bay Region:2002 to 2031.Open-File Report 03-214[R].Washington:U S Geological Survey.
Youngs R R,Coppersmith K J.1985.Implications of fault slip rates and earthquake recurrence models to probabilistic seismic hazard estimates[J].Bull Seismol Soc Am,75(4):939-964.

