基于SPA模型对工业水平衡测试结果评价

□ 崔 岩 任 晔

随着我国经济发展水平及工业化水准的不断提升，相关工业产业需水量日益增大，同时我国现有水资源供给能力有限，造成局部地区用水紧张，如何以有限的水量来满足不断增长的水资源需求量就成为研究水资源的重要课题。对于工业企业用水，在满足生产原料用水的基础上，还需要大量的冷却用水来保证生产线正常运转，工业用水量在整个社会用水总量中所占的比重较大，仅次于农业灌溉用水。因此在工业企业中采取相关节水措施，潜力巨大。

水平衡测试是企业实行节水措施前的一项基础工作，它的成果也是企业对水资源进行科学管理的依据之一，通过水平衡测试，可以系统掌握企业用水现状，让企业有的放矢地挖掘自身节水潜力，水资源测试后形成结果报告，为企业决策者提供决策依据。

我国的水平衡测试起步较晚，现有水平衡测试报告编写也是将测试得到的数据按用水单元进行汇总，以水平衡测试数据结果为基础，结合地方用水定额对用水进行简单评价，还不能给企业的水平衡测试结果进行完整的分级评价，相同类型的工业企业之间不能直观地评优评比。本文以黑龙江华丰煤化工有限公司为例，采用AHP层次分析法和SPA集对分析评价模型相结合，对本次水平衡测试结果进行评价分析。

一、企业水平衡测试

企业水平衡测试是指在一个企业用水体系，在生产过程中，对外来水量和自身循环水量即输入水量，生产使用水量、过程消耗水量、废水排出水量的各个具体量值的调查，并对此用水工程中建立水平衡模型，从而研究内部各个环节用水中存在的问题，并对此不足提出针对性的解决方案，提出合理化的用水方式，其数学模型及循环图如下。

二、SPA集对分析评价模型

集对分析法最初由赵克勤在全国系统理论会上提出（包头，1989），其主要核心内容为将确定性分析和不确定性分析相结合，用于描述和处理综合集成问题的一种新系统分析方法，在研究系统联系中，它从同联系、异联系和反联系三个角度出发，对问题进行分析处理，描述了集合中对子的不同事物的联系，核心思想是将事物确定不确定的视为一个系统，在这个系统中，确定性和不确定性存在一些相关性，彼此影响制约。其核心思想是对事物进行集对从而计算出其联系度，将含有某种关联的两个集合组成对子，根据集合对中某种特性从同、异、反三个角度进行分析，联系度通过联系数公式μ=a+bi+cj（a+b+c=1）来描述，其中：

μ=a+b(同异式) μ=a+cj(同反式) μ=bi+cj(异反式)，以表述其系统的不确定性，最后将不确定性进行定量，转化成数学工具表示。

三、引入实例

利用集对分析模型与华丰煤化工水平衡测试实际数据相结合，对水平衡测试结果进行评价。

将相关各个指标与水平衡评价体系标准进行集对，对于该企业测试指标来说，设定有N个评价指标，其中有S个评价指标处在I标准，F个指标处在II级标准，P个指标处在III级标准，则系统的联系度为：

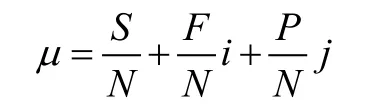
差异系数i、j的确定：其中i为差异不确定系数，取值范围在[-1,1]，当i取值1或-1时，则此时表现为确定性，i越接近于1则联系度越接近于所要评价的级别，i越接近于-1，则联系度越接近于相隔的评价级别，通过阅读相关文献，在水文水资源领域中，一般只考虑相同和相反部分，不考虑相异部分，i取值采用特殊值法即i=0，对立系数j取值为-1。

由水平衡测试分级标准，以本次水平衡测试结果为例，对集对分析模型进行确定联系度，设A为华丰煤化工测试数据的集合，其中各个元素（A1，A2，A3，A4）由四个指标构成，BI、BII、BIII分别为水平衡测试分级标准分布，I、II、III及标准的集合由分表小角标I、II、III指标构成，则（A，BI）、（A，BII）、（A，BIII）组成三个集对，基于集对分析原理，以上两个表为计算依据，计算出联系度。（A，BI）即是本次企业水平衡测试指标和I级的联系度。此时，同联系是指与I级指标相对应，异联系与II级指标相对应，反联系是指与III级指标相对应，由上表资料：本次测试中，符合I级指标同联系的有A1，即S=1；符合II级指标异联系的有A2、A3、A4，即F=3，符合III级指标反联系没有指标，P=0，具体计算见下表：

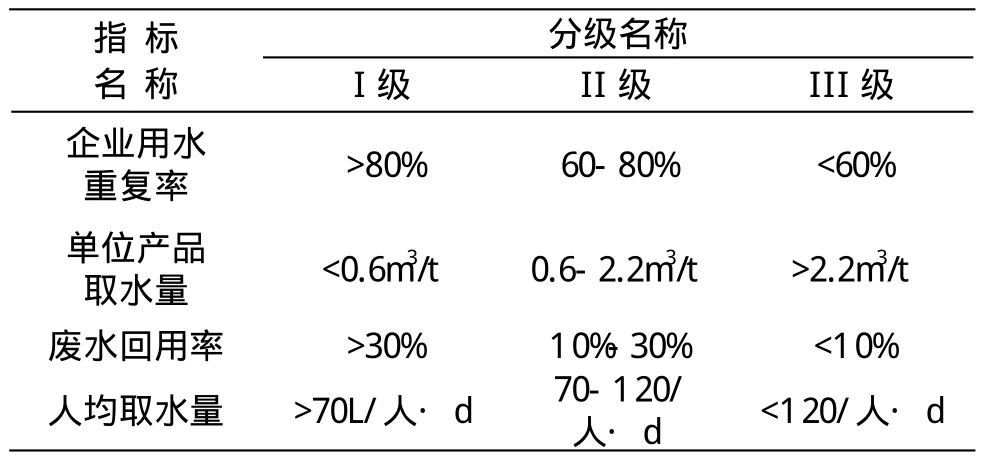
表4-1 华丰煤化工水平衡测试分级标准

表4-2 华丰煤化工水平衡测试分级标准华丰煤化工相关测试结果

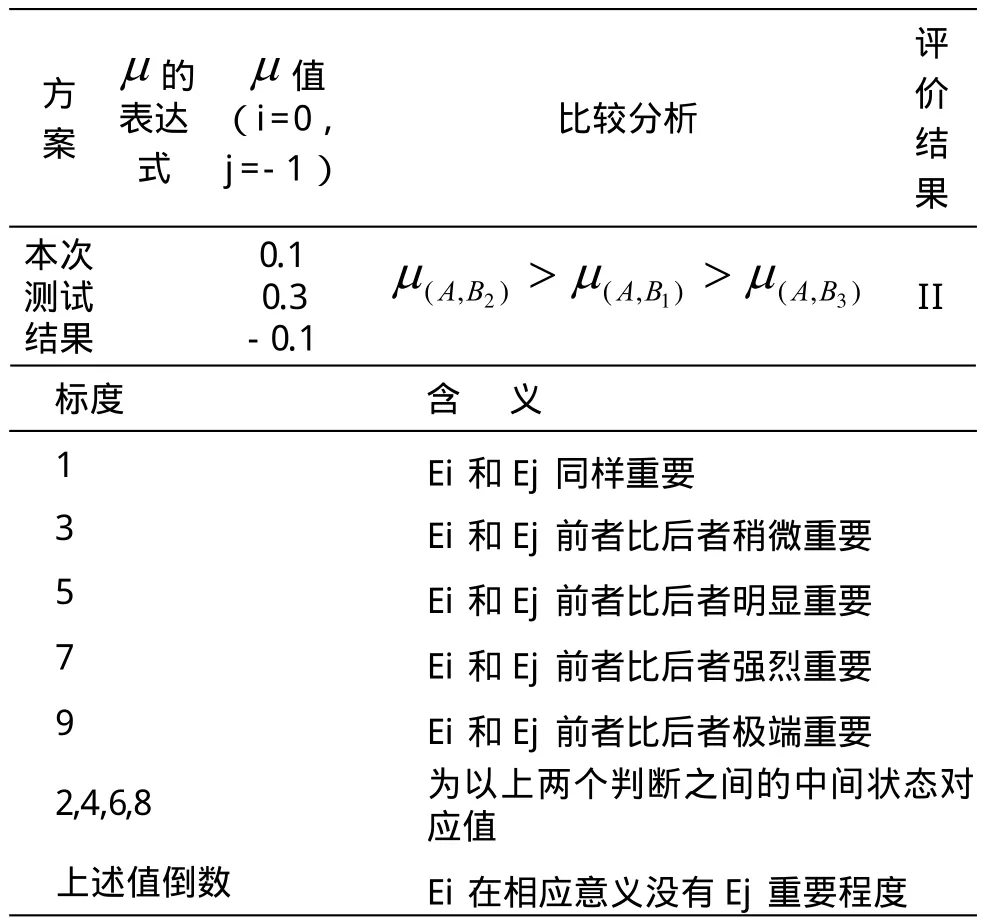
表4-3 联系度计算表及评价结果

四、模糊综合评判模型验证

该模型原理给定两个有限论域u={u1，u2，……，um}；v={v1，v2，……，vm}。其中u代表综合评判因素组成的集合，v代表评语组成的集合。模糊变换B=A·R，A为u上的模糊子集，而评判结果B则是v上的模糊子集，并可表示为：

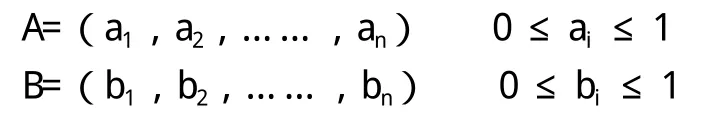
其中，a为ui对A的隶属度，它表示单因素ui在总评定因素中所起作用大小的变量，也在一定程度上代表根据单因素ui评定等级的能力。而bi则为等级vi对综合评定所得B隶属度。表示综合评判结果评判矩阵为：

式中rij表示ui的评价对vj的隶属度。因而矩阵R中第I行Ri=（ri1，ri2，……，rin）即为对第I个因素ui的单因素评判结果。

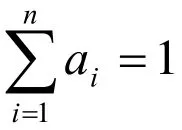
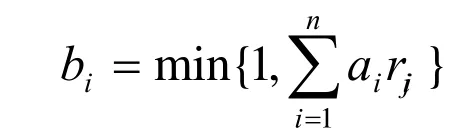
设评价因素为V1、V2、V3， 其 中 V1为 III级，V3为II级。对V1～V3三个等级进行0～1区间评分，a1=0.05,a2=0.5,a3=0.95定量反映，数值越高水平衡测试结果越优秀。

利用层次分析法确定权重：，

表5-1 层次分析法标度对照表

判断矩阵为：

这四个指标的权重向量Wi为：

(0.4921，0.1420，0.3094，0.0565)

求得λmax=4.14

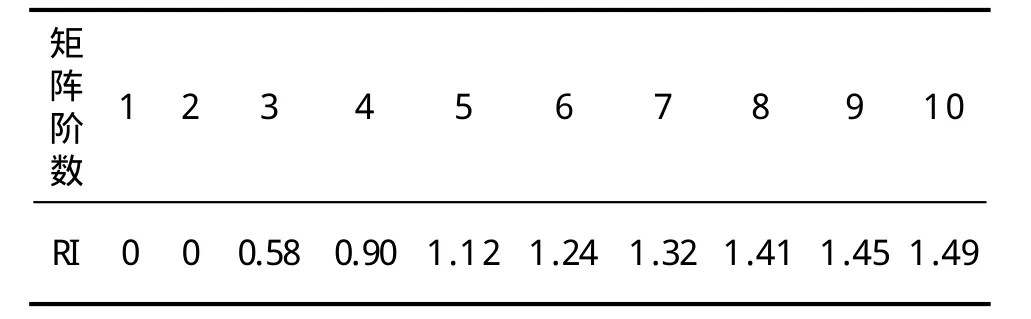
表5-2 RI阶数对照表

查表得RI=0.90，CR=0.0522<0.1，判断矩阵符合要求。

本次水平衡测试数据测度分布矩阵为：

表5-3 模糊综合评判指标表

经过与集对分析评价模型SPA对比，评价一致，都属于II级标准。

五、结束语

集对分析模型对指标多的系统评价有很好的效果，并能一定程度上客观表现该企业的水量，本次水平衡评价过程由于实际测试限制，并没有引入其他关键性指标，尤其是对于漏失水量没有一个具体的衡量，以上两个模型仅供编写报告后对结果评价进行参考，引入的指标越多，对于企业水平衡测试的结果就越完善，由于指标增多，同时也对以后的水平衡测试提出新的测试项目的要求。