粉末注射成形两相流动三维数值模拟及粉末与粘结剂的分离

郑洲顺，曲选辉，徐勤武，李俏杰，刘建康

(1.中南大学 数学与统计学院，长沙 410083；2.北京科技大学 材料科学与工程学院，北京 100083)

粉末注射成形(Powder injection molding，PIM) 是一种源于传统塑料注射成形的粉末冶金近净成形技术。由于其在制作几何形状复杂、组织结构均匀、高性能的近净产品方面具有独特的技术和经济优势而倍受瞩目，被誉为“当今最热门的零部件成形技术”[1-5]。PIM 的充模过程是一个非稳定、非等温的多相流动过程，有固相的粉末颗粒、液相的粘结剂以及模腔中存在的气体,是一个影响因素繁多的非线性动力学系统[6-9]。PIM 的主要工艺过程是首先将粉末与35%～55%(体积分数)的有机粘结剂均匀混炼，并制成粒状喂料，在加热状态下(100～180℃)用注射成形机将熔融状喂料注入模腔内成形。然后，用化学和热分解方法将成形坯中的粘结剂完全脱除，再经烧结致密化得到最终产品[5]。其中注射成形阶段最为重要，因为制品的缺陷基本上是在这一步中引入的，喂料的流变性和粉末粘结剂两相分离是影响 PIM 产品质量的重要因素，两相分离严重时将导致烧结后的成品出现收缩不均等。PIM实验研究中成形坯的粉末密度分布不均以及烧结后的成品出现收缩不均的事实都说明PIM过程中可能发生过粉末粘结剂两相分离的现象，但实验研究难以得到粉末粘结剂两相分离发生的具体位置和时间等信息。如何控制实际生产中粉末粘结剂两相分离现象是一个复杂并需深入研究的问题[10-11]。随着计算机和数值模拟技术的发展，数值模拟分析已广泛应用于PIM技术的研究，为研究PIM缺陷形成机理和工艺参数优化提供重要信息[11-17]。SAMANTA等[10]基于Euler方法建立了一个非等温多相流数值模型，对PIM注射过程粉末粘结剂分离的现象进行了数值模拟。从模拟结果得出，注射温度对粉末粘结剂两相分离的影响比注射速度的影响更大，原因是温度对黏度的影响较大；并对数值模拟结果进行了实验验证。王玉会等[13]应用双流体模型研究了 PIM 充模流动过程中偏析现象，根据充模结束后粉末和粘结剂体积分数的分布情况指出在充模过程中可能存在轻微的偏析。本文作者基于计算流体力学软件CFX对I型拉伸试样和齿轮零件的PIM充模多相流动过程进行三维数值模拟，应用数值模拟方法分析PIM充模过程中粉末粘结剂的两相分离现象，通过分析PIM充模多相流动过程中粉末和粘结剂的流动速度分布及变化情况，对不同位置的粉末和粘结剂速度的变化历程进行对比分析，研究PIM充模流动过程中产生粉末和粘结剂两相分离的位置、时间和相应的特征，为研究粉末注射成形充模流动过程的瞬态情况提供直观的分析手段，为分析和控制产品缺陷提供有用信息。

1 齿轮零件PIM成形坯密度分布

1.1 零件几何模型与实验数据

齿轮零件几何模型参数为外径为1.2 mm、内径为0.56 mm、厚度为0.2 mm，齿轮零件几何模型如图1所示。在对如图1所示的齿轮零件进行PIM实验研究中，采用52%(体积分数)的YG8硬质合金混合粉末与48%(体积分数)的热塑性粘结剂制成注射成形喂料，测得实际使用的粉末和粘结剂的导热系数分别为87.9 W/(m·K)及0.3 W/(m·K)，比热容分别为502 J/(kg·K)和170 J/(kg·K)，密度分别为14.71 g/cm3及0.912 g/cm3。进行注射实验时模具温度300 K、喂料温度443 K、注射速率60 cm3/s。该齿轮零件的PIM成形坯如图2所示。

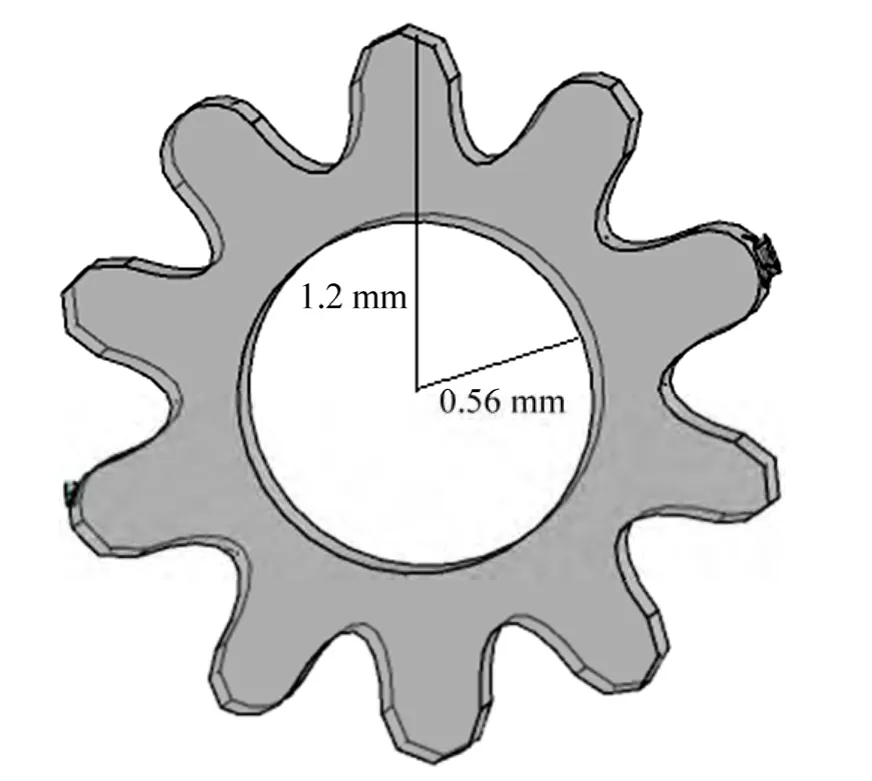
图1 齿轮零件几何模型Fig.1 Geometric model of gear part

图2 齿轮零件的PIM成形坯Fig.2 PIM component of gear part

1.2 齿轮零件PIM成形坯的密度分布情况

经过对齿轮零件 PIM 成形坯的密度进行测试分析，发现成形坯从浇口附近到远离浇口区域粉末密度分布由高到低，有明显梯度。齿轮零件PIM成形坯脱脂烧结后的成品由于收缩不均出现明显的翘曲，远离浇口最后填充的齿轮区域容易出现飞边和塌陷等现象。实验中发现的这些现象说明在齿轮零件PIM成形过程中可能发生过粉末粘结剂两相分离。本文作者采用数值模拟的方法证实齿轮零件PIM成形过程中发生过粉末粘结剂两相分离现象，并分析相应的特征。

2 PIM 充模过程两相流动的双流体模型

根据PIM工艺过程的特点，可假设PIM充模流动过程不发生相变、粉末和粘结剂的密度、导热系数及比热等均为常数。将粘结剂作为连续介质，将粉末颗粒处理为拟流体，即将粉末相也作为连续介质进行处理。

2.1 基本控制方程

在PIM充模流动过程中，粉末和粘结剂既彼此独立又相互作用，两者之间主要通过动量交换和能量交换相互作用。根据多相流理论建立PIM充模过程的粉末和粘结剂流动的控制方程为[13]

质量守恒方程：

式中：k=1，2分别表示液相粘结剂和固相粉末；t为充模时间；φk为相应相的体积分数；vk表示充模过程相应相的速度。

动量守恒方程：

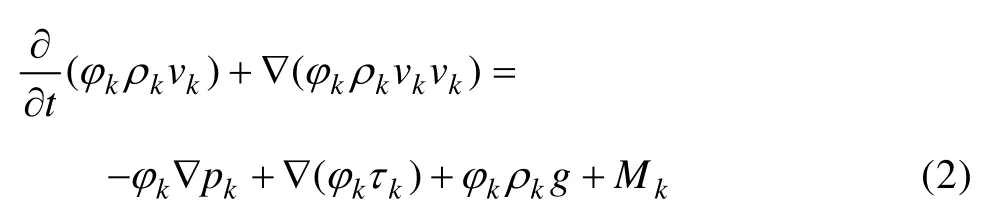
式中：ρk为密度；pk为正应力；τk为剪切应力；Mk表示粘结剂和粉末间的动量交换，且M1=-M2。

能量守恒方程：

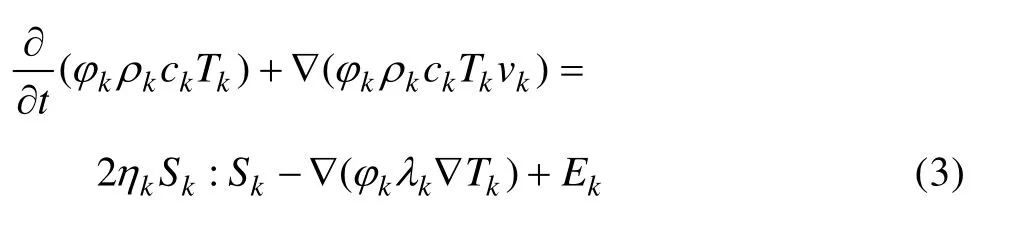
式中：ck为比热容；Tk为温度；ηk为黏度；Sk为应变率张量；Sk:Sk表示张量乘积为Sk的9个相应分量乘积之和；Ek为粘结剂与粉末间的能量交换，且E1=-E2。混合喂料的黏度ηe由粘结剂和粉末两相的黏度η1和η2按(4)计算[14-15]：

2.2 边界条件及初始条件

粉末注射成形充模流动的边界条件由速度、温度、压力边界条件及体积分数构成；初始条件为入口处给定的注射速度、温度及不同物质(空气、粉末相及粘结剂)各自的理论体积分数；固体模壁边界上速度有两种基本假设，即流体满足无滑移条件vwall=0或流体满足滑移条件vwall=v；模腔的排气口处压力为给定的1个标准大气压p0。根据粉末注射成形实际工艺过程参数，数值模拟所用的具体边界条件值如表1所列。

表1 PIM充模流动边界条件Table1 Boundary condition in PIM

3 PIM模具及材料参数

3.1 模腔几何模型与网格剖分

为研究粉末注射成形过程两相分离现象的基本规律，本文作者选用实验研究中常用的Ⅰ型拉伸试样和形状较复杂的齿轮零件进行数值模拟研究。Ⅰ型拉伸试样几何模型参数为长7 mm、宽2 mm、厚1 mm，R5是半径为1 mm的1/4圆，Ⅰ型拉伸试样几何模型如图3所示。

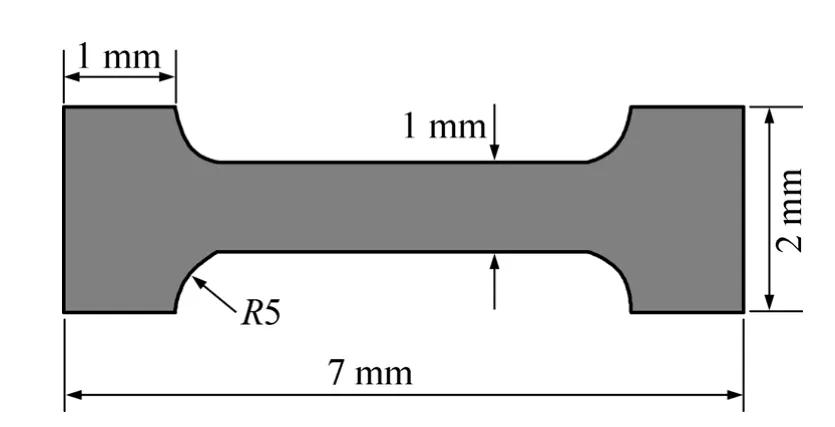
图3 Ⅰ型拉伸试样几何模型Fig.3 Ⅰ-type tensile test specimen

采用四面体网格剖分，剖分节点总数为3 391，单元总数为5 792，网格剖分图如图4所示。针对图1所示的齿轮零件模腔的几何模型，同样采用四面体网格剖，剖分节点数为2 211，单元总数为7 443，网格剖分图如图5所示。

图4 Ⅰ型拉伸试样的网格剖分图Fig.4 Mesh forⅠ-type tensile test specimen

图5 齿轮零件的网格剖分图Fig.5 Mesh for gear parts

3.2 工艺参数与材料参数

为了与实验研究结果进行比较分析，数值模拟采用的PIM工艺参数和材料参数与齿轮零件PIM实验研究的实际参数相同。混合喂料的黏度满足幂率模型[9, 16]

式中：m0=0.34 Pa·sn和Ta=3 512 K，均为与材料有关的常数；T为温度；n为剪切稀化指数，n=0.35，0＜n＜1，γ˙为剪切应变率。粘结剂的黏度η可由流变装置测出，由式(4)可得到粉末的等效黏度。

4 数值模拟结果与粉末粘结剂两相分离分析

4.1 PIM多相流动过程的三维数值模拟

根据实际工艺过程，基于双流体模型用计算流体力学软件CFX对PIM多相流动过程进行三维数值模拟。数值模拟结果表明：在充模过程中，随着时间的推移，模腔中的空气被逐渐排出，最后由粉末和粘结剂的混合喂料填充满整个模腔，整个充模时间为0.25 s。图6所示为粉末注射成形Ⅰ型拉伸试样充模流动过程不同时刻模腔充填的瞬时状态。从图6中可以直观地看到流体前沿面的流动过程，喂料从浇口进入，逐步向前推进，模腔中的空气逐渐从排气口排出。在0.016 s时，喂料前沿到达模腔底部，整个模腔几乎被填满，此时，注射成形充模过程基本结束，剩下的时间是保压阶段。

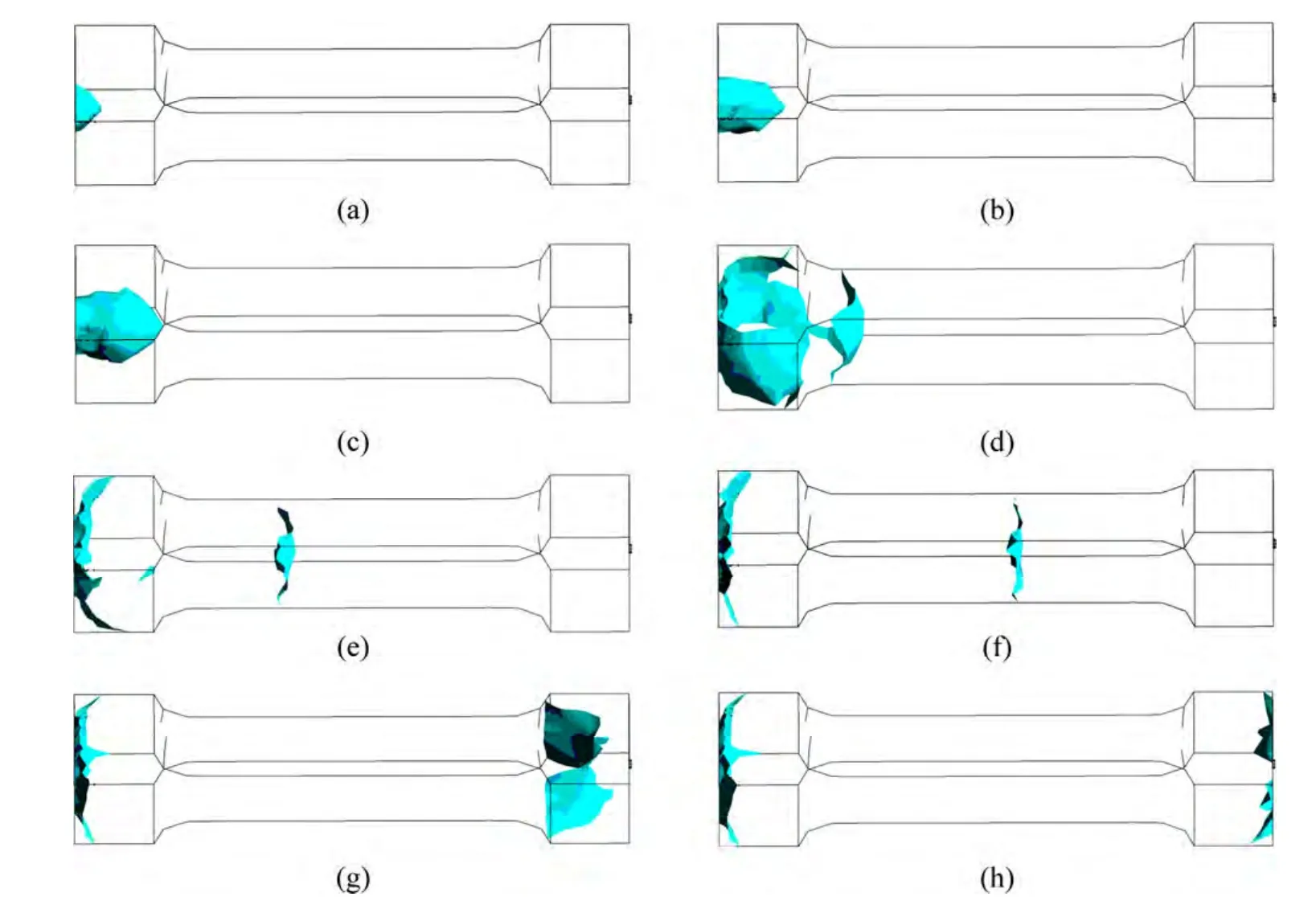
图6 Ⅰ型拉伸试样三维充模流动过程示意图Fig.6 Schematic diagrams of 3D filling process inⅠ-type tensile test specimen: (a) t=0.2 ms; (b) t=0.6 ms; (c) t=1 ms; (d) t=4 ms;(e) t=6 ms; (f) t=8 ms; (g) t=13 ms; (h) t=16 ms

4.2 Ⅰ型拉伸试样模腔内不同位置粉末粘结剂两相分离现象现象

为了分析Ⅰ型拉伸试样PIM充模流动过程中是否发生过两相分离现象，在Ⅰ型拉伸试样模腔中分别选取如图7所示位于浇口附近模腔由宽变窄区域的A点、离浇口较远位于拉伸试样中间狭窄区域的B点和远离浇口位于拉伸试样模腔由窄变宽区域的C点3个结点，根据各点处充模过程中粉末和粘结剂的速度变化情况，判断A、B、C3个点处是否发生过粉末和粘结剂分离的现象及发生粉末和粘结剂两相分离的时间。图8所示为A、B和C点处粉末和粘结剂的速度随充模时间变化的曲线。从图8(a)看出，在整个充模过程中，粉末和粘结剂的速度曲线几乎重合，即粉末和粘结剂的速度差非常小，表明整个充模过程中在A点处没有发生粉末和粘结剂两相分离的现象。

由图8(b)可以看出，B点处粉末和粘结剂两相的速度曲线被充填初期的一小段时间内出现了明显的速度差，说明在该段时间内B点处的粉末和粘结剂产生了两相分离现象，但发生粉末和粘结剂两相分离的时间很短，且在该时间段后，B点处没有再发生两相分离的现象。

由8(c)同样可以看出，在C点处粉末和粘结剂两相的速度曲线被充填初期的一小段时间内出现了较大的速度差，说明在该段时间内C点处的粉末和粘结剂产生了两相分离现象，发生粉末和粘结剂两相分离的时间明显较B点处的长，同样在整个充模流动过程中C点处只在该段时间内产生粉末和粘结剂两相分离现象，之后没有再发生两相分离现象。

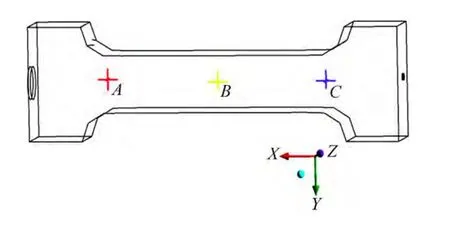
图7 拉伸试样模腔中A、B、C点的位置Fig.7 Locations of points A, B and C inⅠ-type tensile test specimen

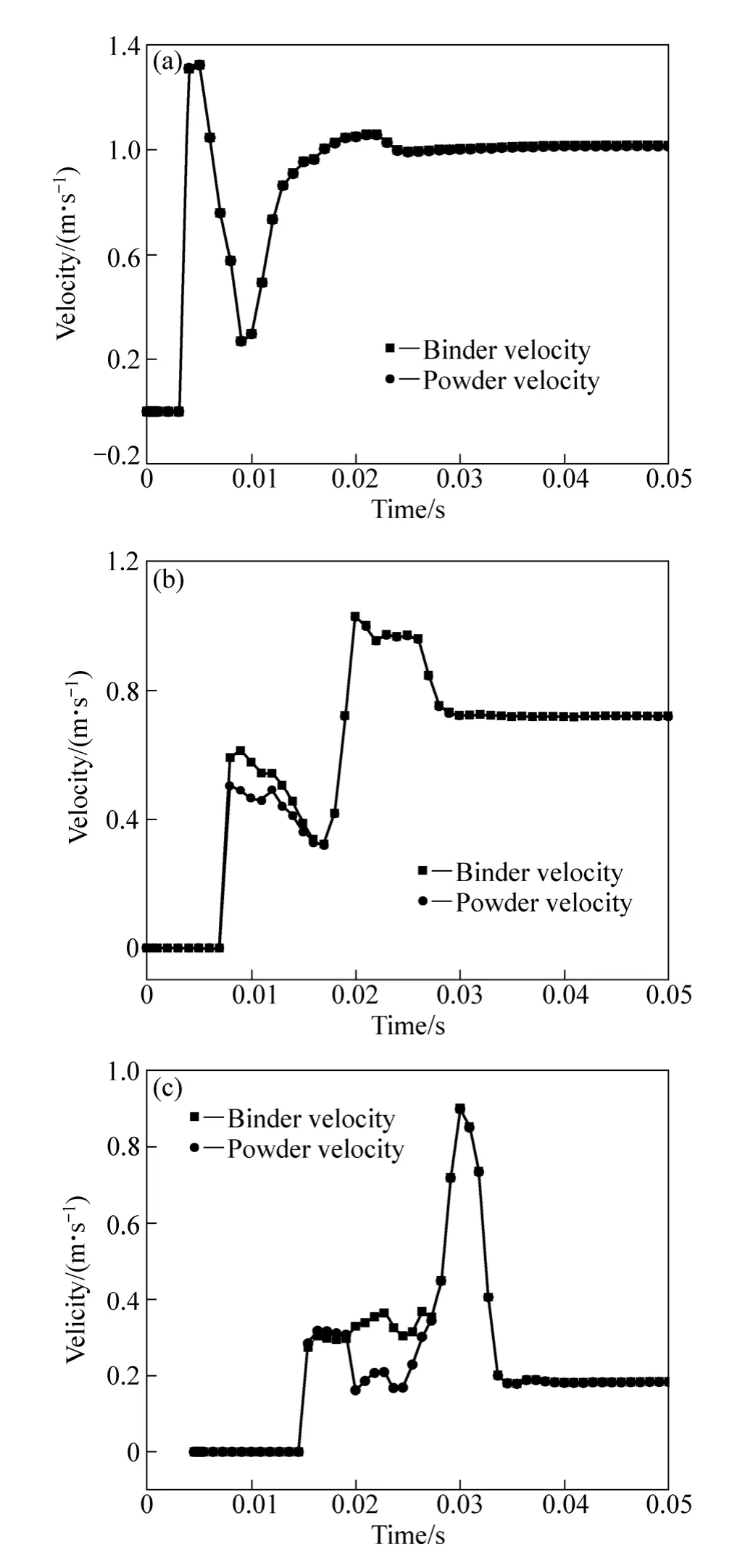
图8 A、B和C点处粉末和粘结剂的速度变化曲线Fig.8 Velocity curves of powder and binder at points A (a), B(b) and C (c)

4.3 齿轮零件模腔内不同位置粉末粘结剂两相分离现象

采用表1中相同的注射参数，对几何形状较为复杂的齿轮零件PIM注射成形的多相流动过程进行了三维数值模拟。在齿轮零件模腔中分别选取如图9所示具有不同位置特征的A、B、C、D4个结点，对PIM充模过程中各点处粉末、粘结剂的速度变化情况进行类似的分析。图10所示为A、B、C、D4个点处粉末、粘结剂的速度随充模时间变化的曲线。

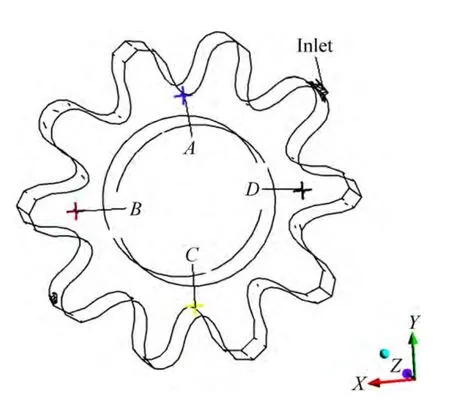
图9 齿轮零件模腔中A、B、C、D点的位置Fig.9 Locations of A, B, C and D points in gear parts

从图10容易看出，在位于浇口较近A点和D点处整个充模过程中粉末和粘结剂的速度曲线几乎重合，即粉末和粘结剂的速度差非常小，表明整个充模过程中在A点和点D处没有发生明显的粉末和粘结剂两相分离现象，但由于A点和D点的空间位置不同，它们的速度变化不同，且粉末、粘结剂的速度差也有明显的差异。在远离浇口的B点和C点处粉末、粘结剂两相的速度曲线在相应位置被充填初期的一段时间内出现了较大的速度差，说明在相应的时间段内，B点和C点处的粉末和粘结剂产生了两相分离现象，粉末和粘结剂两相分离时间都持续很短，在该段时间之后没有再发生粉末和粘结剂两相分离现象。数值模拟结果与实验研究结果都证实齿轮零件PIM成形过程中发生过粉末粘结剂两相分离现象。

4.4 PIM 粉末粘结剂两相分离的位置和时间特征分析

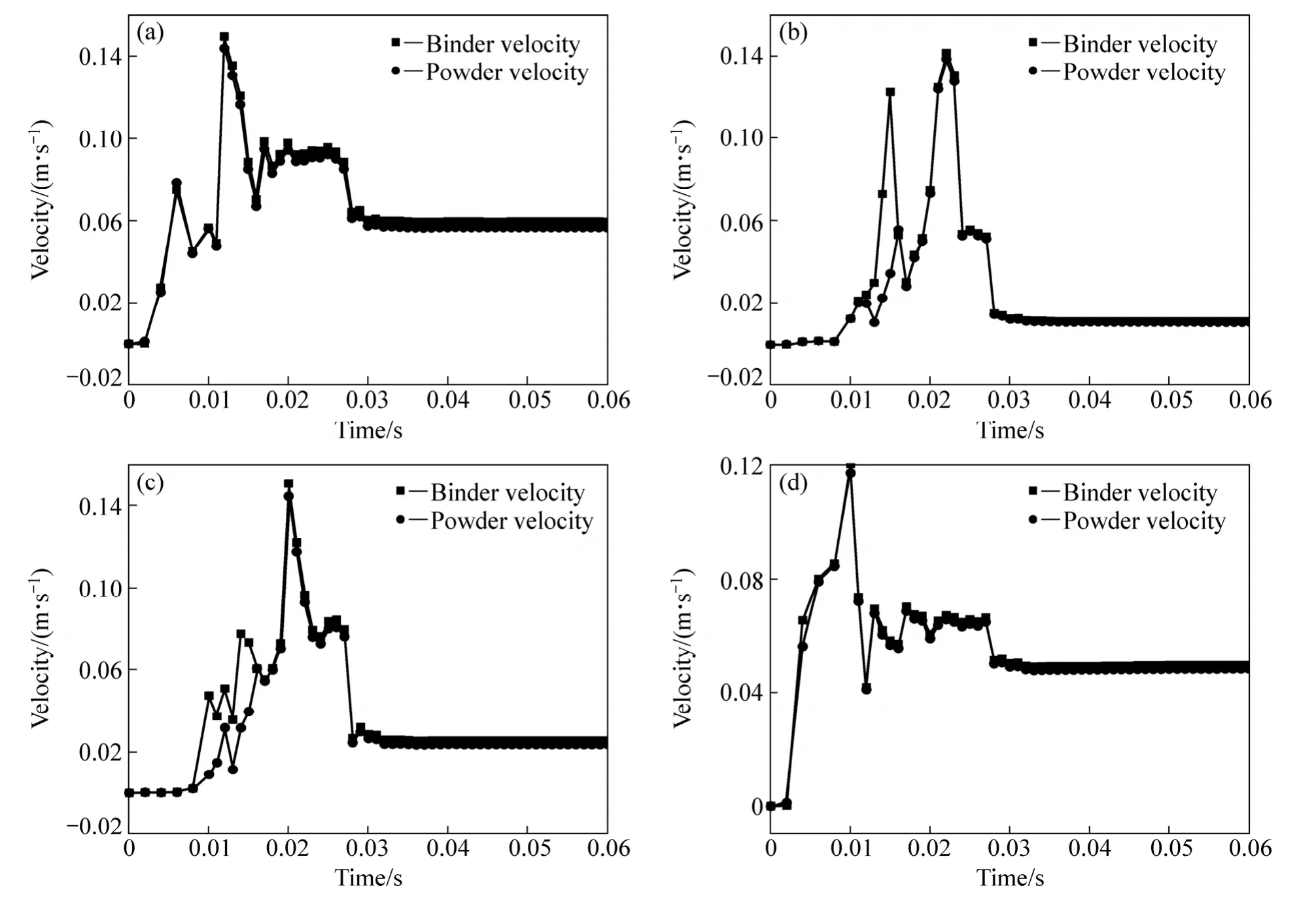
图10 不同点的粘结剂和粉末的速度曲线Fig.10 Velocity curves of powder and binder at different points: (a) A; (b) B; (c) C; (d) D

根据Ⅰ型拉伸试样和齿轮零件模腔PIM多相流动过程的三维数值模拟的结果，通过对Ⅰ型拉伸试样和齿轮零件模腔内多个不同点处粉末、粘结剂速度随充模时间变化曲线的分析。结果表明：PIM充模流动过程中在某些位置会产生不同程度的粉末与粘结剂两相分离现象，位于远离浇口狭窄模腔内的点容易产生两相分离现象；粉末注射成形多相流动过程粉末与粘结剂两相分离现象都是发生在相应位置被充填初期的一段时间内，且该段时间之后不再产生两相分离现象；不同位置发生的两相分离现象持续时间的长短不同、两相分离的程度也不同；粉末与粘结剂两相发生分离时总是粘结剂的速度大于粉末的速度。由于发生粉末与粘结剂两相分离时总是粘结剂的速度大于粉末的速度，因此，远离浇口最后填充的区域粉末的体积分数应低于初始喂料中粉末的体积分数；PIM充模结束时，粉末体积分数分布的数值模拟结果和齿轮零件PIM成形坯脱脂烧结后的成品在远离浇口最后填充的齿轮区域容易出现飞边和塌陷等实验研究结果都印证了这一结论是正确的。

通过对模腔中多个点的粉末与粘结剂两相分离现象的分析，结果表明：PIM过程发生粉末与粘结剂两相分离的位置、时间和程度与模腔的几何形状、注射速率、温度和压力等很多因素相关，而且粉末与粘结剂两相分离的现象只发生在相应位置被充填初期的一段时间内，可见通过PIM实验研究难以分析粉末粘结剂两相分离的现象。因此，对给定的几何模腔和注射参数，数值模拟方法是分析研究PIM过程中的粉末与粘结剂两相分离的现象、探索PIM成形坯缺陷产生的原因和控制方法的一条有效途径。

5 结论

1) 根据齿轮零件 PIM 成形坯密度分布梯度以及成品容易出现飞边和塌陷位置的实验研究结果，指出PIM实际成形过程中可能发生过粉末与粘结剂两相分离现象。

2) 基于计算流体力学软件CFX实现了PIM充模多相流动过程的三维数值模拟，为研究PIM过程相关因素的瞬态分布和时间历程变化情况提供了直观分析方法。

3) 在PIM 充模流动过程中模腔的某些位置曾经发生过不同程度的粉末与粘结剂两相分离现象，且PIM过程中各点处是否发生两相分离现象与模腔的几何形状、注射速率和注射温度等很多因素相关。

4) PIM充模流动过程中位于远离浇口狭窄模腔内的点容易产生粉末与粘结剂两相分离现象、两相分离现象只发生在相应位置被充填初期的一段时间内、粉末与粘结剂两相发生分离时总是粘结剂的速度大于粉末的速度、不同位置发生的两相分离现象持续时间的不同等一般规律。

5) 齿轮零件PIM实验研究结果和相应的数值模拟分析结果说明PIM过程中粉末与粘结剂两相分离是影响成形坯粉末密度分布和成品质量的重要因素。

[1]曲选辉.粉末注射成形的研究进展[J].中国材料进展, 2010,29(15): 42-47.QU Xuan-hui.Advance in research of power injection molding[J].Materials China, 2010, 29(15): 42-47.

[2]GERMANN R M, HUANG K X.The condition of MIM, PIM and relative PM technology in the USA[J].Powder Metallurgy Technology, 2006, 24(5): 384-387.

[3]赵小娟, 党新安.金属粉末注射成形技术及模具的研究现状[J].模具技术, 2008, 5: 11-14, 62.ZHAO Xiao-juan, DANG Xin-an.The status of metal powder injection molding technology and the mold[J].Die and Mould Technology, 2008, 5: 11-14, 62.

[4]ROSOF B H.The metal injection molding process comes of age[J].Journal of Materials, 1989, 41(8): 13-16.

[5]GERMAN R M.Powder injection molding[M].Princeton, NJ:Metal Powder Industries Federation, 1991.

[6]SAMANT S K, CHATTOPADHYAY H, PUSTAL B, BERGER R, GODKHINDI M M, BÜHRIG-POLACZEK A.A numerical study of solidification in powder injection molding process[J].International Journal of Heat and Mass Transfer, 2008, 51(3/4):672-682.

[7]刘 烨, 曲选辉, 尹海清.数值模拟工艺参数对氧化铝陶瓷微齿轮注射成形影响[J].粉末冶金技术, 2010, 28(5): 381-386.LIU Ye, QU Xuan-hui, YIN Hai-qing.Effect of the process parameters on alumina ceramic micro-gear Injection molding in numerical simulation[J].Powder Metallurgy Technology, 2010,28(5): 381-386.

[8]郑洲顺, 曲选辉, 韩旭里, 张国栋.粉末注射成形充模流动过程模壁凝固层增长的计算与模拟[J].中国有色金属学报,2008, 18(3): 511-515.ZHENG Zhou-shun, QU Xuan-hui, HAN Xu-li, ZHANG Guo-dong.Computation and simulation of solidification on wall of cavity in powder injection molding filling process[J].The Chinese Journal of Nonferrous Metals, 2008, 18(3): 511-515.

[9]郑洲顺, 曲选辉, 雷长明.PIM充模流动过程中粘度的变化与缺陷形成[J].金属学报, 2007, 43(2): 187-193.ZHENG Zhou-shun, QU Xuan-hui, LEI Chang-ming.Defects and variation of viscosity in powder injection molding filling process[J].Acta Metallurgica Sinica, 2007, 43(2): 187-193.

[10]SAMANTA S K, CHATTOPADHYAY H, GODKHINDI M M.Modelling the powder-binder separation in injection stage of PIM[J].Progress in Computational Fluid Dynamics, An International Journal, 2011, 11(5): 292-304.

[11]JENNI M, SCHIMMER L, ZAUNER R, STAMPFL J, MORRIS J.Quantitative study of powder binder separation of feedstocks[J].Powder Injection Moulding International, 2008,2(4): 50-55.

[12]王玉会, 曲选辉, 何新波, 张 勇, 赵丽明.硬质合金粉末注射成形偏析现象的数值模拟[J].稀有金属与硬质合金, 2008,36(2): 10-14.WANG Yu-hui, QU Xuan-hui, HE Xin-bo, ZHANG Yong,ZHAO Li-ming.Numerical simulation of segregation in injection moulding of cemented carbide powder[J].Rare Metals and Cemented Carbides，2008, 36(2): 10-14.

[13]王玉会, 曲选辉, 何新波, 张 勇, 赵丽明.粉末注射成型过程的双流体数学模型[J].机械工程材料, 2008, 32(5): 74-77.WANG Yu-hui, QU Xuan-hui, HE Xin-bo, ZHANG Yong,ZHAO Li-ming.Two-fluid model during powder injection molding process[J].Materials for Mechanical Enginering, 2008,32(5): 74-77.

[14]范小欣.MIM注射多相流模拟的各相本构和边界条件滑移[D].成都: 西南交通大学, 2006.FAN Xiao-xin.Viscous behaviours of each phase and wall slip in bi-phase simulation of the MIM injection[D].Chengdu:Southwest Jiaotong University, 2006.

[15]封 娟, 何 浩, 李益民, 王光耀.粉末共注射成形充模流动过程前沿位置及场分布的数值模拟[J].中国有色金属学报,2012, 22(8): 2333-2339.FENG Juan, HE Hao, LI Yi-min, WANG Guang-yao.Numerical simulation of melt front and filed profile in powder coinjection molding filling process[J].The Chinese Journal of Nonferrous Metals, 2012, 22(8): 2333-2339.

[16]NOVAC O A, ANTON D, NOVAC T.The rheological behavior of some binders and plastics used in injection molding[J].Powder Metallurgy, 1994, 94: 113-120.

[17]HWANG C J, KWON T H.A full 3D finite element analysis of powder injection molding filling process including slip phenomena[J].Ploymer Engineering and Science, 2002, 42(1) :33-50.