针铁矿法沉铁过程的混杂建模与控制

陈 宁，范 勇，桂卫华，阳春华，蒋朝辉

(中南大学 信息科学与工程学院，长沙 410083)

锌是重要的有色金属原材料，在国民经济各个领域中占有十分重要的地位，广泛应用于有色冶金、机电、化工、汽车等行业。湿法炼锌是金属锌的主要生产方法，采用该工艺所生产的锌占世界锌总产量的80%以上。目前，冶炼企业大都采用高铁硫化锌精矿为原料的湿法冶炼方法，由于硫酸锌浸出溶液中铁离子的含量很高，而铁离子在净化和电解过程中被视为有害离子，因此，该工艺过程的核心技术就是杂质铁的脱离，也就是沉铁技术。针铁矿法沉铁由于铁渣中含铁量高、结晶大、易过滤、夹带有价金属少，经适当预处理可作为炼铁富矿使用，是除铁工艺过程中最常用方法[1]。

为了实现沉铁工艺过程优化和自动控制，建模是最为关键的一步。由于连续搅拌反应釜(CSTR)工艺流程能够处理高悬浮固体含量原料，反应器内部物料分布均匀，适于大规模生产，大多数化工工业过程都使用该流程工艺。基于连续搅拌反应釜(CSTR)建模方法在化工工业过程中应用的非常广泛[2-4]，邓燕妮等[5]和SIAVA等[6]针对连续搅拌反应釜(CSTR)过程建立了反映系统动态变化的机理模型。王凌云[7]针对富锌溶液中镉、钴离子的净化过程，由物料平衡原理建立锌粉除杂的CSTR动态反应模型。上述作者都是在过程内在机理分析的基础上，利用物料守恒，化学反应平衡以及化学动力学等推导出过程CSTR机理模型的方法，该方法能够提取复杂系统的本质和主流因素，便于实现对复杂化工过程的数学描述，而且这些研究为人们对CSTR机理建模的本质有了更深入的理解。但机理建模需要避免冗长、复杂、繁琐的方程堆砌，这就不可避免地以牺牲模型精度为代价。

针铁矿法沉铁过程设备多、工艺条件要求严格、过程内部动力学特性极为复杂，是一个非线性强工艺过程。对于非线性系统的混杂建模在理论上取得了丰硕的成果[8-10]，但在工业实践中混杂系统理论的应用中存在的很多问题还没有得到很好的解决。王蓬等[11]针对化工生产过程连续反应釜的高度非线性特性，利用实际工况的数据离线辨识建立多个局部模型，通过设计每个子模型 GPC控制器进而实现整个工业过程的良好控制效果。DU等[12]针对连续搅拌反应釜系统非线性、多点运行，以及运行范围宽等特点，利用混合逻辑动态系统描述该系统的混杂特性，最后通过模型预测控制设计各切换子系统的控制器。

本文作者针对某冶炼生产企业针铁矿法沉铁过程，深入研究沉铁过程的反应机理以及溶液 pH值、温度、铁离子浓度、氧气流量等一系列因素对沉铁过程中氧化、水解以及中和反应的影响。利用物料守恒和化学反应平衡原理，对沉铁过程中3个主要化学反应进行动态描述，建立基于Fe2+浓度和有效溶解氧浓度的混杂模型。该建模方法能够准确地描述实际系统动态变化的过程，很好地解决了传统单一机理模型精度低，模型易失配的问题，为提高我国锌冶炼过程自动控制水平，实现冶金工业过程节能降耗提供新的思路和方法。最后通过数值计算和仿真说明了所建立混杂模型的有效性。

1 针铁矿法沉铁过程机理分析

某冶炼生产企业针铁矿法沉铁工艺流程图如图1所示，该流程是一个基于连续搅拌反应釜的长流程工艺过程，涉及一系列复杂的气、液、固三相化学反应过程，沉铟后液和沉铁上清液流入反应器1中经过氧化、水解及中和反应后，溢流到反应器 2、3、4、5参与反应，除铁后液经反应5溢流后过滤，最后沉铁上清液又泵入反应器1中。

在整个沉铁循环过程中，Fe2+的氧化速率和pH值是两个关键的控制参数，沉铁过程中Fe2+的氧化速率过快会使短时间内Fe3+的含量过高，影响水解反应的正常进行；氧化速率过慢，会使沉铁后液铁离子含量超标，达不到需要的除铁效果。针铁矿的形成必须要在Fe3+浓度很低情况下得以生成，当溶液pH值太低时，会降低沉淀效率；而pH值太高，又使其他成分发生不必要的沉淀，降低氧化锌中和剂的反应性。当溶液Fe3+浓度和pH值都较高时，将导致Fe3+快速沉淀而生成胶体。溶液中Fe2+浓度对氧化速度影响较大，在Fe2+浓度比较大时，反应速度比较快，随着溶液中Fe2+浓度的减少，反应速度变得越来越慢。因此，整个循环过程中需要不断调节焙砂和氧气的输入量，保证各反应器中铁离子浓度和pH值在一定的工艺范围内。熊富强等[13]通过对针铁矿法沉铁过程Fe2+的氧化、Fe3+的水解以及中和3个主要的化学反应过程的研究，详细分析影响沉铁效果的两个关键工艺参数：氧化速率和pH值。

图1 某冶炼生产企业针铁矿法沉铁工艺流程图Fig.1 Flow chart of iron precipitation by goethite process in smelting enterprise

3个主要化学反应如下。

氧化反应：

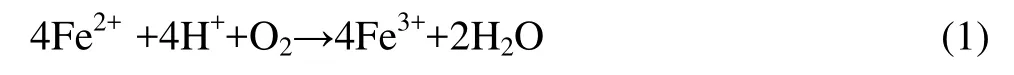
水解反应：

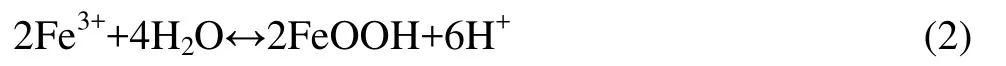
中和反应：

由上述3个化学反应可以看出该反应组是一个强耦合的过程，在Fe2+的氧化及中和反应中，H+均为反应物，随着反应的进行，溶液中的H+浓度降低了，而Fe3+的水解反应又一定程度提高H+的浓度。特别地，Fe3+的水解反应是一个可逆的过程，Fe3+在溶液中很不稳定，能以很快的速度形成简单水解产物，其水解沉淀过程相当复杂。

要最终形成针铁矿型铁渣，需要极度苛刻的条件。实际工况过程中反应器5出口Fe3+浓度需始终保持在1g/L以下且又不能太低，pH值为2.5～4之间，Fe3+才更容易水解形成针铁矿沉淀。

2 针铁矿法沉铁过程机理模型的确定

2.1 建立沉铁过程各离子浓度变化的平衡方程

针对针铁矿法沉铁过程中3个主要的化学反应过程，分析 Fe2+、Fe3+、H+的反应速率，并由物料守恒原理分别建立对应的质量平衡方程。假设整个沉铁过程温度恒定，反应器1入口流量F恒定，反应器容积为V，容器内溶液搅拌均匀，且催化剂催化作用已达到理想状态。

1) 在Fe2+氧化反应中，根据化学动力学方程可知，Fe2+氧化速率可表示为

式中：k1为反应速率常数；α、β、γ为反应级数；cFe2+、cH+、cO2分别为Fe2+浓度、H+浓度和溶液中的有效溶解氧浓度。

由物料平衡定理，Fe2+的氧化过程可建立如下平衡方程：

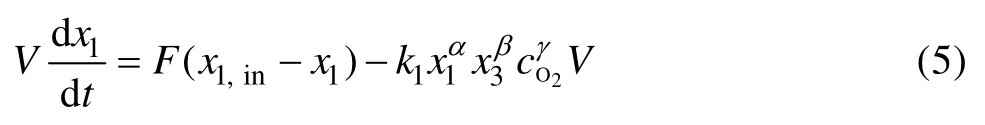
式中：x1为溶液中Fe2+浓度；x1,in为反应器1入口Fe2+浓度；x3为溶液中H+浓度。

2) 结合针铁矿的形成机理可知 Fe3+水解反应生成单核FeOH2+，它是形成的针铁矿主要离子。FeOH2+离子浓度近似表示为

式中：β0为单核FeOH2+水解的平衡常数。那么，Fe3+的反应速率可表示为

式中：ka、kb为反应速率常数，可通过辨识得到。

由物料平衡定理，Fe3+水解反应过程的平衡方程为

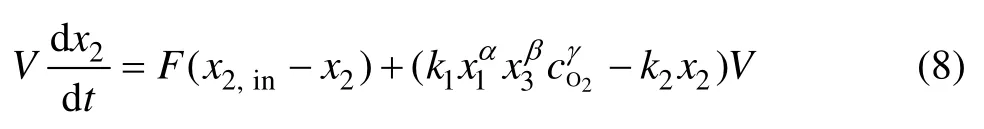
式中：x2为溶液中Fe3+浓度；x2,in为反应器1入口Fe3+浓度。

3) 在中和反应中焙砂呈固体颗粒状，现假设反应过程中焙砂颗粒为球状且大小不变，反应过程主要是H+的液膜扩散，由缩芯模型理论可知[14]，单位时间内参与反应 H+的速率就是焙砂颗粒通过液膜到达颗粒外表面H+的数量，可表示为

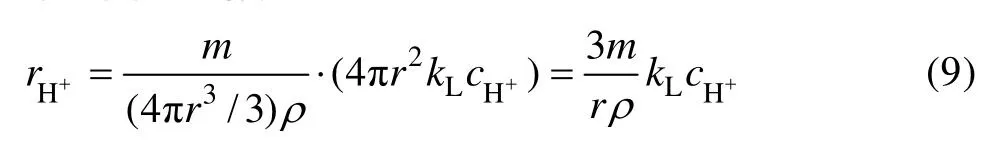
式中：r为焙砂颗粒半径；cH+为氢离子浓度；ρ为焙砂单颗粒密度；m为焙砂的总质量；kL为液膜传质系数，可由参数辨识获得。

由物料平衡定理，中和反应过程H+浓度变化的平衡方程为

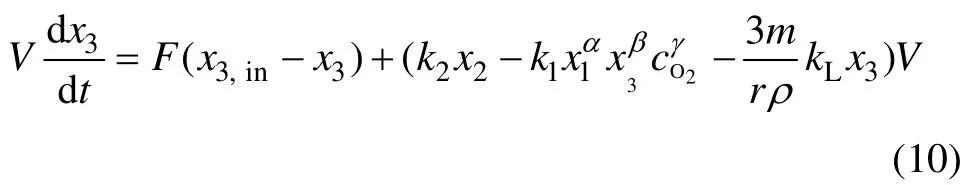
式中：x3为溶液中H+浓度；x3,in为反应器1入口Fe3+浓度。

2.2 建立有效溶解氧浓度模型

由于整个沉铁工艺过程工况多变，每个反应器中各离子浓度存在较大差异。其中Fe2+浓度对氧气在溶液中的溶解度影响较大，当Fe2+浓度波动时，溶液中的有效溶解氧浓度将会发生很大变化[1,15-16]。由双膜理论[17]、渗透理论和表面更新理论[18]，分析Fe2+浓度不同波动范围内溶液中有效溶解氧浓度的模型。此时，假设溶液温度一定，各反应器搅拌均匀。

1) 当Fe2+浓度较高时，溶液的含固量一定，鼓入溶液中的氧分子主要通过扩散与Fe2+参加氧化反应，此时溶液中溶解氧与氧流量呈正比关系。当氧气流量达到一定量，由于溶液本身 (离子浓度、溶剂等因素)的影响，溶液中氧含量将不再增大。因此，沉铁反应器溶液中有效溶解氧浓度与氧气流量可近似表示为

式中：FO2为为通入反应器的氧气流量；η为调节系数，可通过参数辨识获得。

2) 正常工艺条件下，Fe2+浓度在合理的工艺范围内波动，溶液中液相本体对氧气的吸收推动力减弱，液相界面的氧流量和氧分压对液相本体的氧浓度起到共同的作用。此时，反应器溶液中有效溶解氧浓度可表示成：

式中：pO2为通入反应器的氧分压；λ1和λ2为多元回归系数，可通过参数辨识获得。

3) 当Fe2+浓度较低，溶液中氢离子、Fe2+和Fe3+浓度对氧浓度的影响程度增强。通过对实际工况采集数据进行分析，氧浓度与氧气流量近似为表示为

式中：pH为采样周期内沉铁反应器出口 pH值的平均值；λFe为上一个采样时刻沉铁反应器出口Fe3+浓度与Fe2+浓度之比，γ0和γ1为一元回归系数，可通过参数辨识获得。

2.3 沉铁过程Fe2+浓度下降梯度和pH值设定

针铁矿法沉铁过程各反应器Fe2+浓度下降区间和pH值需要在一个合理的范围，若Fe2+浓度下降梯度曲线过缓或过陡(如图2中的梯度曲线1和曲线4)，将影响出口Fe2+浓度值，使得出口浓度不达标，造成出口溶液成份的剧烈波动，导致下一级反应器不能稳定运行，甚至会影响最终针铁矿型铁渣的品位，而无法生成针铁矿型的铁渣。

此外，在氧化和中和反应中，H+均作为反应物参与反应，且H+浓度过高又会影响水解反应的进行。为提高沉铁过程各化学反应的反应速率，需要合理设定各反应器内溶液的酸平衡度。

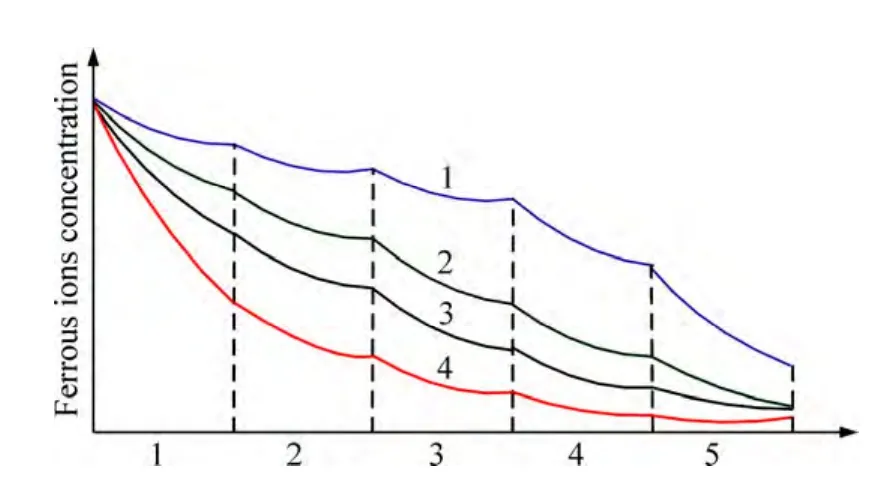
图2 沉铁过程Fe2+浓度梯度变化曲线Fig.2 Gradient curves of Fe2+ concentration during iron precipitation process

实际工艺过程，反应器1入口铁离子浓度、pH值以及入口流量等对Fe2+浓度的状态变化有较大影响，水解和中和反应又直接影响Fe2+的氧化过程。根据实际工业过程现场采集的生产数据，Fe2+浓度的最优下降梯度约束为

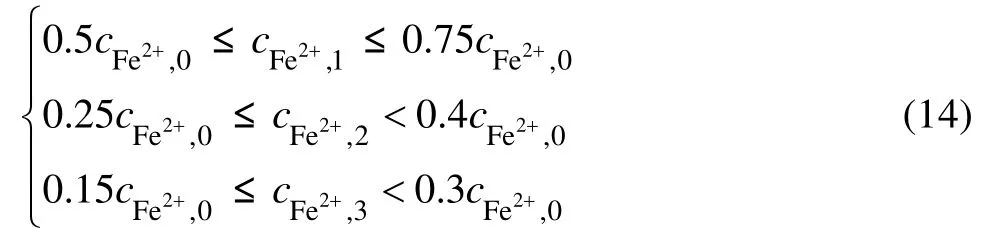
式中：cFe2+,1、cFe2+,2、cFe2+,3和cFe2+,0分别为反应器1、2、3以及反应器的入口Fe2+浓度。

3 混杂建模控制方法

混杂系统模型一般可表示为

式中：f∈Rn×Rm，g∈Rn×Rm，x(t)∈Rn为系统状态变量；u(t)∈Rm为系统控制变量；σ∈Λ{1，2，3，…，N}为系统切换律。

针铁矿法沉铁过程的一个最关键的工艺参数就是溶液中Fe2+的氧化速率，它对沉铁反应器中Fe3+过饱和度和有效溶解氧浓度有较大影响。在实际工艺过程，由于无法保证反应器入口溶液中Fe2+浓度恒定，而且反应过程中又受到包括外界温度、催化剂等影响，导致整个沉铁过程中Fe2+浓度波动较大。因此，利用Fe2+浓度的波动区间对实际工况进行分类，建立基于Fe2+浓度和有效溶解氧浓度的切换模型，并根据不同工况条件下的实际工业生产数据辨识模型参数。设cO2=uσ，则

令vσ(x1,x2,x311)=xασxβσuγσσ，求解系统(16)的平衡点为

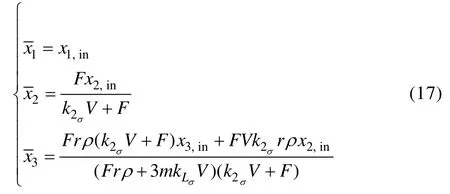
由于系统(16)平衡点不在原点，对系统做如下平移

线性化系统(16)为

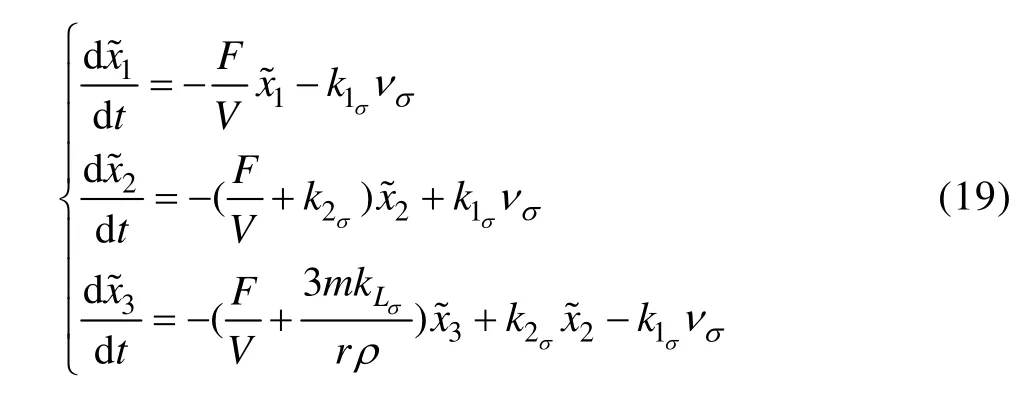
式(19)表示成：

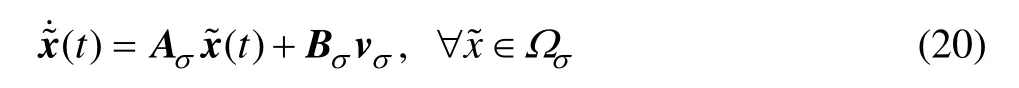
式中：+σΩ⊆R表示状态空间的各封闭子区域

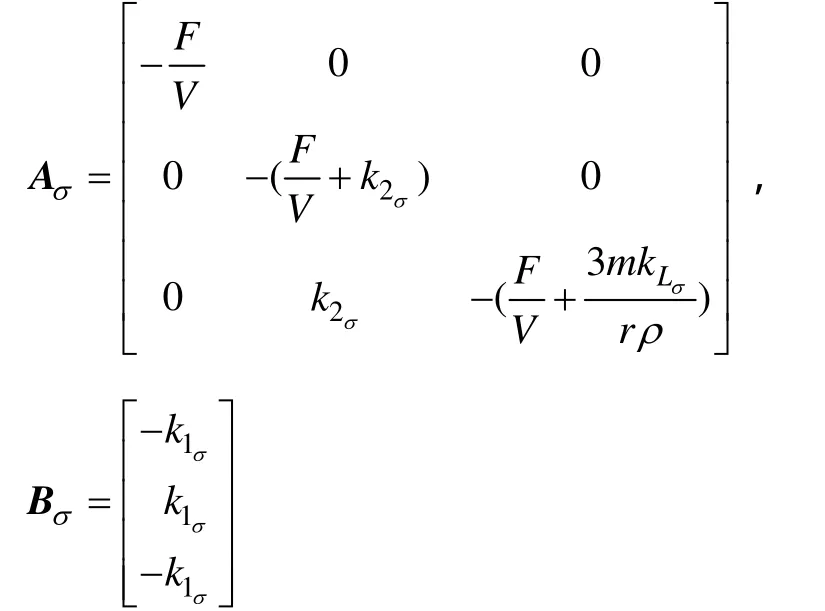
设计系统(20)反馈控制器为

式中：K∈Rl×n为系统状态反馈增益矩阵，且Kσ中σ每个元素都必须正。

定理1 对于系统(20)，在各封闭子区域内Ωσ如果存在对角正定矩阵Y和矩阵L，使得如下线性矩阵不等式成立

则对于xΩ+∀∈⊆R内，由系统(20)和控制器(21)组成的闭环系统在任意切换律下是渐近稳定的，对应的控制器为Kσ=LY-1。

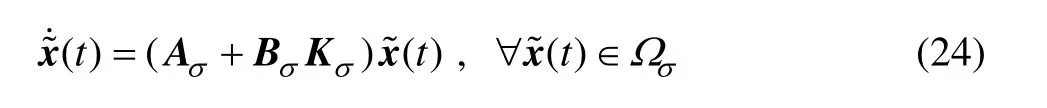
证明：将式(21)代入式(20)中，可得到闭环系统为保证在Ω+⊆R内，闭环系统(24)在任意切换律下的渐近稳定性，可构造如下公共Lyapunov函数

式中：P为正定矩阵。

对式(25)求导可得

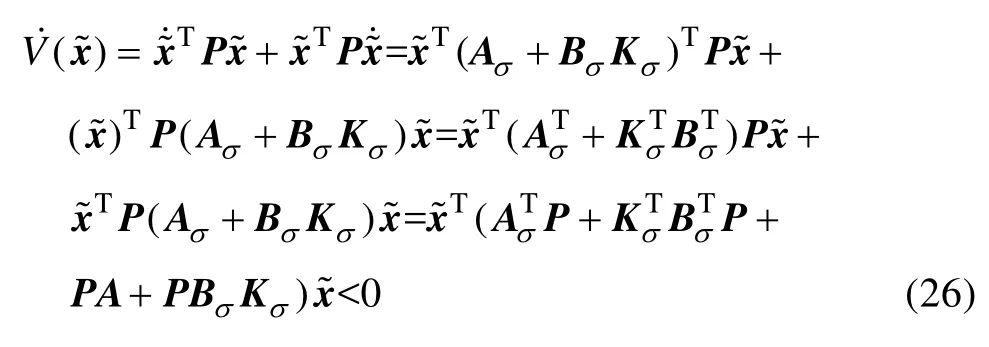
不等式(26)等价于

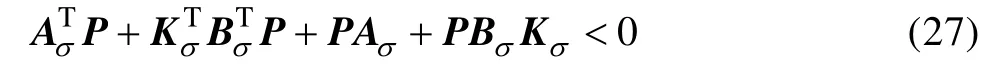
对不等式(27)分别左乘和右乘diag{P-1，I}，可得公式(21)，Y=P-1。

而式(23)成立可以保证每个反应器的控制输入都是正的。

求解式(22)和(23)可以得到系统(20)控制器vσ，对应系统(16)的控制器为

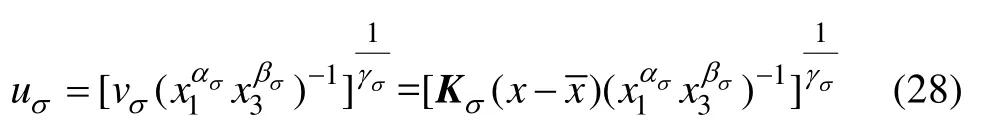
由式(28)就可根据状态x1的分段区间分别按照式(11)～(13)求解不同铁离子浓度下的氧气流量的大小,从而实现对沉铁过程的有效控制。

4 数值计算与仿真分析

对于系统(16)，σ为依赖于系统状态变量x1(即Fe2+浓度值)和系统输入量u(即溶液中有效溶解氧浓度)的系统切换律。根据实际工艺指标，式(16)中切换律可表示为

由工业生产数据，采用最小二乘法对不同切换律(29)下系统(16)中的参数进行辨识，结果如表1所列。

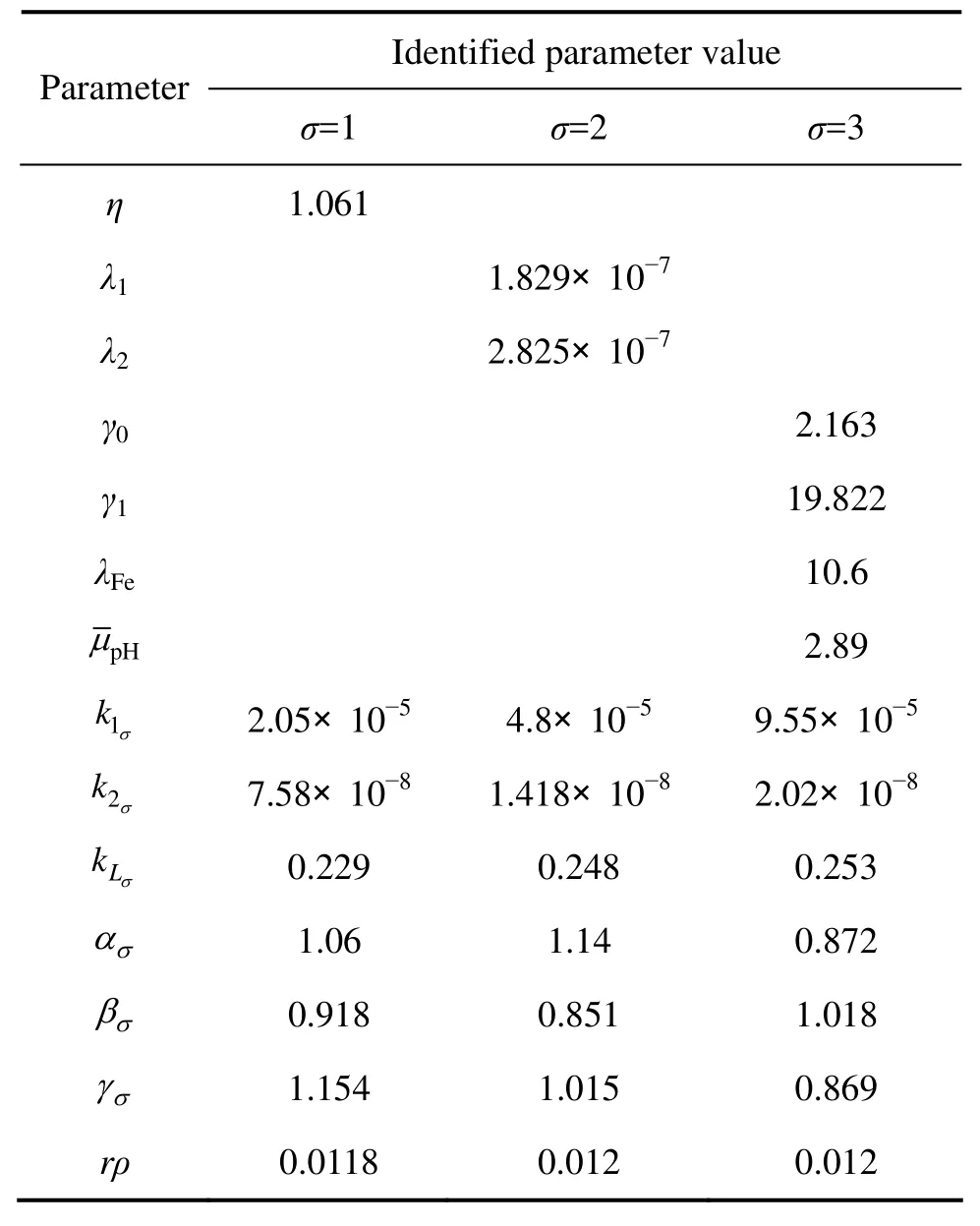
表1 反应器1不同工况下参数辨识结果Table1 Parameter identification results of tank 1 under different conditions

设沉铁过程中反应器入口流量和反应器的有效容积分别F=231 m3/h，V=300 m3；取x1,in=13 g/L，x2,in=1.2 g/L，x3,in=1×10-3g/L。

求解不等式(26)和(27)得P和Kσ分别为

在整个沉铁过程中，溶液中氧气输入量的控制主要取决于氧气流量的大小，单反应器氧气输入时氧压几乎恒定不变。结合实际生产过程，反应器氧气输入压力可取值为pO2=1.5 MPa。由式(11)～(13)，求得对应切换律(28)下，氧气输入流量表达式为

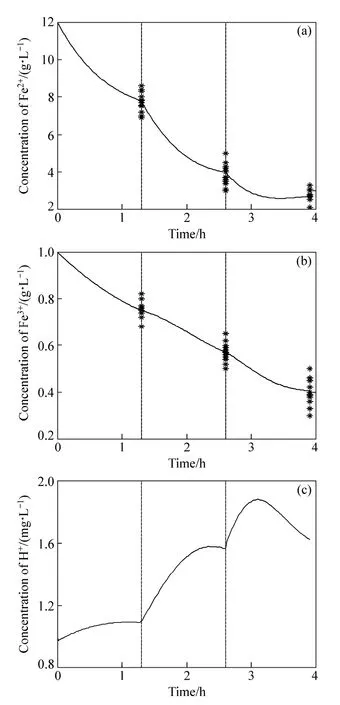
图3 Fe2+、Fe3+和H+浓度变化曲线Fig.3 Concentration change curves of Fe2+ (a), Fe3+ (b) and H+ (c)

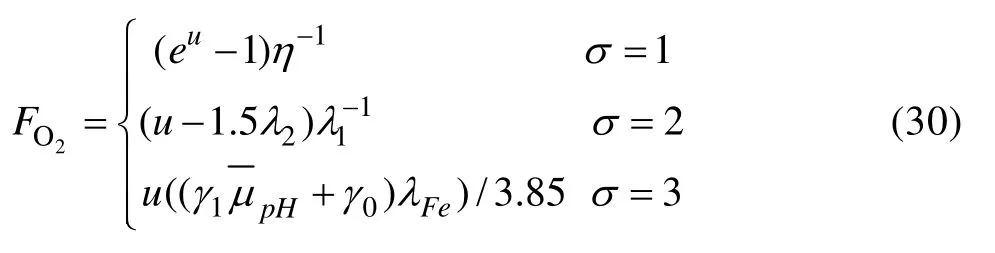
各反应器中，化学反应过程受到包括反应物浓度、温度、催化剂以及搅拌强度等多种因素的影响，传统单一的机理模型精度低，模型易失配。为了说明该混杂模型的有效性，下面将通过仿真分析并结合文献[13]来进行说明。从图3中可看出，仿真结果很好地反映出沉铁过程中铁离子浓度的变化过程。整个沉铁过程中H+浓度变化很小，仿真曲线符合实际的生产过程H+浓度变化。从上述仿真结果分析可以看出本研究提出的混杂建模控制方法能够很好地反映不同工况下系统的状态变化过程，体现出该混杂模型控制方法的有效性。

5 结论

1) 针铁矿法沉铁过程机理复杂、强非线性且边界约束条件苛刻，传统建模方法仅仅依靠对过程的机理分析进而建立一个统一的模型，这就导致模型的精度低、模型易失配的问题。在沉铁过程机理模型的基础上，利用实际生产采集的数据对沉铁过程进行分类，由混杂系统理论，建立了随溶液中Fe2+浓度变化的有效溶解氧浓度模型的沉铁系统混杂模型。

2) 通过线性化系统方程后，利用公共 Lyapunov函数方法设计了各子模型控制器。由实际生产数据对建立的混杂模型进行了参数辨识。

3) 仿真结果说明混杂建模方法能够有效地解决传统单一机理建模出现的问题，很好地反映出复杂多变的实际生产过程，该方法也为今后冶金工业领域的建模提供了新的思路。

[1]陈家墉, 于淑秋, 伍志春.湿法冶金中铁的分离与利用[M].北京: 冶金工业出版社, 1991: 1-441.CHEN Jia-yong, YU Shu-qiu, WU Zhi-chun.Separation and utilization of iron in hydrometallurgy[M].Beijing:Metallurgical Industry Press, 1991: 1-441.

[2]MATTOS A G, PINTO J C.Steady-state modeling of s1urry and bulk propylene polymerizations[J].Chemical Engineering Science, 2001, 56(13): 4043-4057.

[3]SVANDOVA Z, KOTORA M, MARKOS J, JELEMENSKY L.Dynamic behaviour of a CSTR with reactive distillation[J].Chemical Engineering Journal, 2006, 119(2/3): 113-120.

[4]JONESA P N, OCAN-TASKIN N G, YIANNESKIS M.The use of momentum ratio to evaluate the performance of CSTRs[J].Chemical Engineering Research and Design, 2009, 87(4):485-491.

[5]邓燕妮, 桂卫华, 阳春华, 谢永芳.氧化铝碳酸化分解动态过程建模及非线性分析[J].中国有色金属学报, 2008, 18(9):1736-1741.DENG Yan-ni, GUI Wei-hua, YANG Chun-hua, XIE Yong-fang.Dynamic process modeling and nonlinear analysis for alumina carbonation decomposition[J].The Chinese Journal of Nonferrous Metals, 2008, 18(9): 1736-1741.

[6]SLAVA J, SVANDOVA Z, MARKO J.Modelling of reactive separations including fast chemical reactions in CSTR[J].Chemical Engineering Journal, 2008, 139(3): 517-522.

[7]王凌云.湿法炼锌净化过程建模及基于控制参数化的优化方法[D].长沙:中南大学, 2009: 39-47.WNAG Ling-yun.Modelling and optimization method based on control parameterization in purification process of zinc hydrometallurgy[D].Changsha: Central South University, 2009:39-47.

[8]程代展, 郭宇骞.切换系统进展[J].控制理论与应用, 2005,22(6): 954-960.CHENG Dai-zhan, GUO Yu-qian.Advances on switched systems[J].Control Theory and Applications, 2005, 22(6):954-960.

[9]BALDI S, BATTISTELLI G, MOSCA E, TESI P.Multi-model unfalsified adaptive switching supervisory control[J].Automatica, 2010, 46(2): 249-259.

[10]BALDI S, IOANNOU P, MOSCA E.Multiple model adaptive control with mixing: The discrete-time case[J].IEEE Transactions on Automatic Control, 2012, 57(4): 1040-1045.

[11]王 蓬, 李少远.一类非线性系统的多模型预测控制[J].控制与决策, 2007, 22(10): 1113-1118.WANG Peng, LI Shao-yuan.Multiple model based predictive control for a class of nonlinear systems[J].Control and Decision,2007, 22(10):1113-1118.

[12]DU Jing-jing, SONG Chun-yue, LI Ping.Modeling and control of a continuous stirred tank reactor based on a mixed logical dynamical model[J].Chinese Journal of Chemical Engineering,2007, 15(4): 533-538.

[13]熊富强, 桂卫华, 阳春华, 李勇刚.基于针铁矿法的沉铁过程动态建模[J].中南大学学报: 自然科学版, 2012, 43(2):541-547.XIONG Fu-qiang, GUI Wei-hua, YANG Chun-hua, LI Yong-gang.Dynamic modeling for process of iron precipitation based on goethite method[J].Journal of Central South University:Science and Technology, 2012, 43(2): 541-547.

[14]SZEKELY J, EVANS J W.A structural model for gas- solid reactions with a moving boundary[J].Chemical Engineering Science, 1970, 25(6): 1091-1107.

[15]李仕雄.硫酸锌溶液中针铁矿法沉铁的氧化过程[J].有色冶金, 1982(2): 40-44.LI Shi-xiong.The oxdation process of iron removal by the method of goethite from zinc sulfate[J].Non-ferrous Metallurgy,1982(2): 40-44.

[16]陈耐生, 赵经贵, 张滨秋.对针铁矿法除铁过程中亚铁离子氧化速度的研究[J].黑龙江大学: 自然科学学报, 1984, 1(3):76-80.CHEN Nai-sheng, ZHAO Jing-gui, ZHANG Bin-qiu.Research on oxdation speed of ferrous ion with the process of ir on removal by the method of goethite[J].Journal of Heilongjiang University: Natural Science, 1984, 1(3): 76-80

[17]张洪流.化工原理—传质与分离技术分册[M].北京:国防工业出版社, 2009: 70-143.ZHANG Hong-liu.The principle of chemical engineering mass transfer and separation technology volume[M].Beijing: National Defence Industry Press, 2009: 70-143.

[18]王晓红.化工原理[M].北京: 化学工业出版社, 2009:263-330.WANG Xiao-hong.The principle of chemical engineering[M].Beijing: Chemical Industry Press, 2009: 263-330.