分布式MIMO雷达稀布阵列研究

金 镇，谢良贵，文树梁

(1.中国航天科工集团二院二十三所，北京100854;2.中国航天科工集团公司，北京100048)

0 引言

远程雷达探测任务对雷达威力要求越来越大，分布式MIMO雷达［1－4］可解决大功率孔径积与机动性的矛盾，因而成为研究热点，但实用上必须解决栅瓣问题。以往文献中，解决栅瓣问题的方法有稀布阵［5－6］、虚拟孔径［7－9］和等效相位中心法［10－13］等，基本限于平面阵列的优化。在实际应用中，分布式MIMO雷达阵列布置在一个平面上，单元雷达竖起一定角度，阵面法线指向监视空域，具有三维阵列特点，在密集布置时需兼顾遮挡问题，给栅瓣抑制带来困难，本文正是讨论这种情况下的阵列优化布局。本文提出满足无遮挡约束下PSL最小的阵列优化准则以抑制栅瓣，对比不同阵列布局、不同单元雷达数量与孔径、扫描情况下PSL水平，为分布式MIMO雷达阵列布局提供选择依据。对于分布式雷达中单元雷达数量与孔径的选择，以往文献中很少提及，本文将随机阵列理论［14］引入分布式雷达，讨论了单元雷达数量与孔径对PSL的影响。

1 阵列模型

1. 1 无遮挡约束

分布式相参MIMO雷达阵列模型如图1(a)所示，单元雷达在XOY平面上随机布置，各单元雷达天线法向与Z轴之间的夹角为α。

单元雷达位置受天线阵面仰角与波束扫描范围的限制。考虑单元雷达间不能互相遮挡主瓣，忽略对副瓣的遮挡，得到下面的单元雷达无遮挡约束。

图1 分布式MIMO雷达模型Fig.1 Model of distributed MIMO radar

如图2(a)所示，前后放置的两个天线阵面AB和CD，天线阵面宽度都为h，与水平面夹角都为α，波束最大扫描角β。则根据几何关系，可知前后放置的单元雷达间距需满足下式

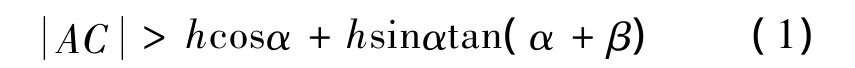
单元雷达水平间距也需满足约束，如图2(b)所示，当阵面A'B'E'F'沿直线A'B平行移动时，其扫描波束不会被阵面ABEF遮挡。可得

综合以上，为了波束扫描时单元雷达不相互遮挡主瓣，每个单元雷达周围一定区域内不能摆放其它雷达，这个区域是由两个等腰梯形拼接成的图形，如图2(c)中所示，图中相应参数为

图2(c)中直线OA与等腰梯形的斜边具有相等斜率，当单元雷达相位中心连线的斜率小于OA的斜率时，例如单元雷达沿X轴排列，单元雷达间距可以较近甚至紧密排列;而当单元雷达相位中心连线的斜率大于OA的斜率时，例如沿Y轴排列，单元雷达垂直间距必须大于ymin，间距较大。

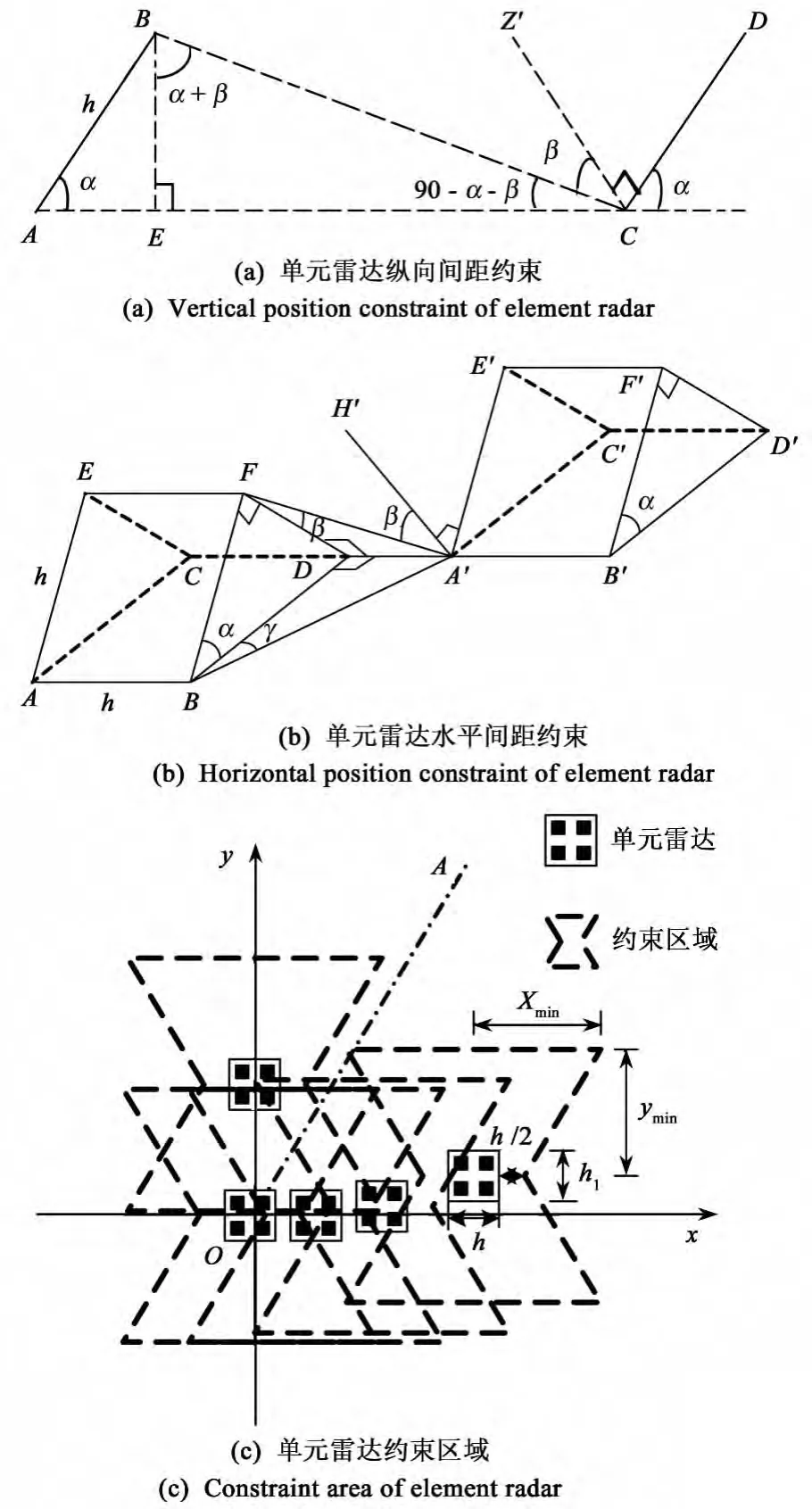
图2 单元雷达无遮挡约束示意图Fig.2 Sketch map of element radar’constraint area

1. 2 方向图表示

雷达阵列坐标系为XYZ，雷达阵面坐标系为X'Y'Z'，如图1(b)所示。其中 X'轴与 X轴重合，Y'/Z'轴由Y/Z轴绕OX旋转角度α得到，旋转变换矩阵A如下

阵列坐标系下单元雷达位置 xk=［xk，yk，

设单元雷达的方向图为 f(θ，φ)，单元雷达的阵因子为 a(θ，φ)= ［a1(θ，φ)，a2(θ，φ)，…，aN(θ，φ)］T，

其中 λ 为载波波长，ux= ［sinθcosφ，sinθsinφ，cosθ］T，ux0= ［sinθ0cosφ0，sinθ0sinφ0，cosθ0］T。

根据方向图相乘原理，阵列的导向矢量可表示为c(θ，φ)= ［c1(θ，φ)，c2(θ，φ)，…，cN(θ，φ)］T，其中 ck(θ，φ)=ak(θ，φ)f(θ，φ)，i=1，2，…，N。

MIMO雷达发射－接收联合波束方向图表示为

与由等效相位中心方法得到等效阵列的远场双程方向图相同［11］。

分布式MIMO雷达阵列优化问题可表述为

2 单元雷达数量与孔径对副瓣影响

Steinberg得到随机阵列峰值副瓣电平q与副瓣方差 σ2的比［14］

其中β称为置信水平，是对副瓣区域进行n次采样幅度都不超过q的概率，n是副瓣区域采样点数，与可见区域副瓣个数有关。

将信号s(t)与频谱S(f)的傅里叶变换，与电流密度I(x)和远场辐射方向图F(u)的关系作一对比:

可见，f↔u，t↔x/λ，时宽T↔L/λ，带宽W↔u的非冗余可视区域，采样点数n=WT↔uL/λ。

分布式雷达中，非冗余可视区域 u =π(sinθ3dB)2，采样点数 n= π(L sinθ3dB/λ)2，其中 L为阵列一维的孔径，θ3dB=0.88λ/(cosθBD)是单元雷达方向图主瓣宽度，其中D为单元雷达孔径，θB为扫描角。

N个收发共用天线有N2个收发共置的等效相个，因而可等效为(N2+N)/2个收发同置的独立天线组成的相控阵雷达，副瓣方差近似为σ2=2/N2。

将σ2与n代入式(8)，得到单元雷达数量N与孔径D对峰值副瓣q影响如式(9)所示，在置信水平β=0.95时，绘成曲线如图3所示。

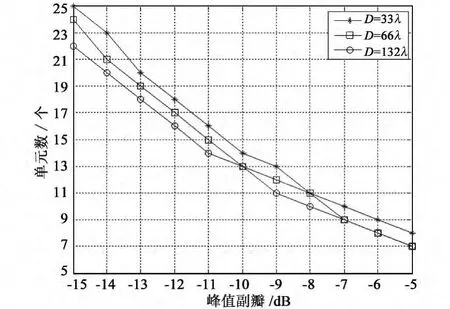
图3 单元雷达数量与孔径对PSL影响Fig.3 Element radar number and aperture’s effect on PSL

3 仿真分析

以X波段(fc=10GHz)分布式MIMO雷达为例，对不同布局下联合波束方向图进行仿真。并设定单元雷达阵面倾角45度，扫描范围正负30度。选择19个单元雷达，每个天线阵面由132个天线单元按λ/2紧密排列组成，由图3可知这样的阵列配置可以得到大约－13dB的PSL。

分布式MIMO雷达阵列基本布局如图4所示，包括六边形阵列(图4(a))、圆环阵列(图4(b))和扰动圆环阵列(图4(c))。六边形阵列在X'Y'面上的投影为正六边形，单元雷达间距为250λ。圆环阵列在X'Y'面上的投影为标准圆环，外环半径500λ由16个单元雷达组成，内环半径266λ由3个单元雷达组成。

图4(c)采用小位置扰动、大位置扰动和PCA优化方法3种不同扰动方式。小位置扰动将单元雷达位置扰动限制在40λ之内，大位置扰动将单元雷达位置扰动限制在150λ之内。PCA是综合孔径稀布阵列优化中常用方法，可用来抑制栅瓣，其优化目标是阵列等效相位中心构成满阵［13］。

通过粒子群优化算法(Particle Swarm Optimization，PSO)［15］，得到三种扰动圆环阵列的单元雷达位置扰动量，如表1所示。

将不同阵列布局下方向图中PSL所在剖面进行对比如图5所示，PSL结果如表2所示，其中阵列形式与图5相对应。

六边形阵列可以看成两个按矩形排列阵列的组合，因而栅瓣位置应按照矩形排列的阵列计算，其单元雷达沿X轴方向间距dx=250λ，沿Y轴方向间距dy=612λ，Y方向栅瓣位置在 sinθ－ sinθ0=nλ/dy，n=1，2，3，…，θ0=45°，第 一 栅 瓣 位 置0.18°，处于单元雷达主瓣宽度 θ3dB=51λ/D=0.76°之内，因此在方向图中存在较高副瓣，峰值副瓣 －3.1dB，这个副瓣是由第一栅瓣形成的。如果单元雷达沿Y轴均匀排列，受无遮挡约束限制最小为ymin，所以沿Y轴方向栅瓣很密集。

表1 单元雷达位置扰动量Table 1 Perturbation of element radar position

表2 PSL仿真结果Table 2 Simulation results of PSL

由图5(b)、(c)、(d)、(e)可见，规则排列的圆环阵可以获得－12dB的PSL，扰动圆环阵可以得到更低的PSL。三种扰动方法相对比，圆环阵列+大位置扰动可得到最低PSL，另两种方法得到PSL相接近。分析其原因，圆环阵列+小位置扰动、圆环阵列+大位置扰动都以最低峰值副瓣为优化目标，而圆环阵列+PCA优化方法以获得等效相位中心最接近满阵为优化目标，这从本质上决定了前两种方法可获得更低峰值副瓣。

由于实际阵列大部分时间工作在扫描状态下，需对扫描情况下性能进行分析。图6是圆环阵列+大位置扰动得到的优化阵列在若干扫描角度下的三维方向图，这里选取了一些副瓣较高的扫描角度，由方向图得到扫描情况下PSL为－18dB，因此圆环阵列+大位置扰动在扫描情况下的性能是满足要求的。

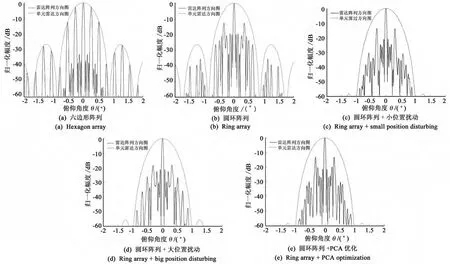
图 5 阵列方向图 (θ0=0°，φ0=0°)Fig.5 Pattern of array(θ0=0°，φ0=0°)

图6 圆环阵列+大位置扰动方向图(θ0=30°)Fig.6 Pattern of Ring array+big position disturbing(θ0=30°)

4 结论

本文研究分布式MIMO雷达阵列优化布局问题。不同于平面相控阵，分布式MIMO雷达的单元雷达阵面竖起一定仰角，有三维阵列特点。讨论了防止单元雷达间相互遮挡的约束条件，得到此约束下PSL最小的阵列优化准则。利用随机阵列理论，分析单元雷达数量与孔径对PSL的影响，用于指导优化过程中单元雷达数量与孔径的选择。对比了六边形阵列、圆环阵列、圆环阵列+不同扰动方式的PSL水平，得出结论，在分布式MIMO雷达紧密布阵且无遮挡情况下，六边形阵列栅瓣抑制能力最差，圆环阵列有较好栅瓣抑制效果，由本文优化准则得到的圆环阵列+大位置扰动可更有效抑制栅瓣，不扫描情况下PSL优于文献［13］中采用的等效相位中心优化方法，扫描情况下PSL也满足应用要求，为分布式MIMO雷达阵列布局提供了选择依据。

［1］ Robey F，Pulsone N.Wideband aperture coherence processing for next generation radar， ADA430577［R］. Lexington:Massachusetts Inst.of Tech，Lexington Lincoln Lab，2004.

［2］ Coutts S，Cuomo K.Distributed coherent aperture measurements for next generation BMD radar［C］.Fourth IEEE Workshop on Sensor Array and Multichannel Processing.Washington:IEEE Press，2006:390－393.

［3］ Fishler E，Haimovich A.MIMO radar:an idea whose time has come［C］.The IEEE Radar Conference，Newark:New Jersey Inst.of Tech.，2004:71 －78.

［4］ 陈浩文，黎湘.一种新兴的雷达体制－MIMO雷达［J］.电子学报，2012，40(6):1190－1198.［Chen Hao-wen，Li Xiang.A rising radar system-MIMO radar［J］.ACTA Electronica Sinica，2012，40(6):1190 －1198.］

［5］ 史学书，王元钦.深空大规模天线阵布局优化方法研究［J］.宇航学报，2010，31(2):478 －484.［Shi Xue-shu，Wang Yuanqin.Research of optimizing algorithm for deep space large arrays geometric Configuration［J］.Journal of Astronautics，2010，31(2):478 －484.］

［6］ Reberts W，Xu L Z.Sparse antenna array design for MIMO active sensing applications［J］.IEEE Transaction on Antennas and Propogation，2011，59(3):846－858.

［7］ Stoica P，Li J.On probing signal design for MIMO radar［J］.IEEE Transaction on Signal Processing，2007，55(8):4151 －4161.

［8］ Fuhrmann D，Antonio G.Transmit beamforming for MIMO radar systems using signal cross-correlation［J］.IEEE Transactions on Aerospace and Electronics，2008，44(1):171－186.

［9］ 许红波，倪菁.一种分布式阵列波达方向估计方法［J］.宇航学报，2012，33(12):1801 － 1805.［Xu Hong-bo，Ni Jing.An estimation of DOA methods based on MIMO distributed arrays［J］.Journal of Astronautics，2012，33(12):1801 －1805.］

［10］ 邢孟道，李真芳.分布式小卫星雷达空时频成像方法研究［J］.宇航学报，2005，26(10):70 － 82.［Xing Meng-dao，Li Zhen-fang.Study of distributed microsatellites radar space-timefrequency imaging method［J］.Journal of Astronautics，2005，26(10):70 －82.］

［11］ 林月冠，张冰尘.一种基于压缩感知的高分辨率宽测绘带合成孔径雷达成像算法［J］.宇航学报，2013，34(1):106－112.［Lin Yue-guan，Zhang Bing-chen.HRWS SAR imaging based on compressed sensing［J］.Journal of Astronautics，2013，34(1):106 －112.］

［12］ 张晓玲.一种消除三维合成孔径雷达图像栅瓣的方法:中国，200910059548.2［P］.2009 －06 －10.

［13］ 侯颖妮，李道京.基于稀疏综合孔径天线的艇载成像雷达研究［J］.电子学报.2008，36(12):2377－2382.［Hou Yingni，Li Dao-jing.Airship imaging radar based on aperture synthesis of thinned array［J］.Acta Electronica Sinica，2008，36(12):2377 －2382.］

［14］ Steinberg B.The peak sidelobe of the phased array having randomly located elements［J］.IEEE Transaction on Antennas and Propogation，1972，20(2):129－136.

［15］ 金镇，籍刚.共置天线的分布式相参MIMO雷达布阵优化研究［J］.系统工程与电子技术，2012，34(12):65 －69.［Jin Zhen，Ji Gang.Optimizing antenna array geometry for distributed coherent MIMO radar with collocated antennas［J］.Systems Engineering and Electronics，2012，34(12):65 －69.］