利用光学测量改进火星探测器巡航段定轨预报精度

吴功友，杨 悦，王西京，刘 宇

(1.宇航动力学国家重点实验室，西安710043;2.四川大学软件学院，成都610065;3.上海航天控制工程研究所，上海210000)

0 引言

自从1962年以来，人类就开始了火星探测的征程。先后有苏联的“火星”系列、“福布斯”系列、“火星探路者”系列，美国的“水手”系列、“海盗”系列，以及欧洲、日本等国的火星探测器对火星进行了不懈的探测，对火星的地形地貌、大气环境、水土特性等取得了第一手资料。目前，火星上是否存在生命仍然是一个未解之迷，也正因为如此，火星成为各国深空探测的热门焦点［1］。随着我国航天实力的不断增强和月球探测工程的成功实施，我国也积极加入到了火星探测的队伍。2011年随俄罗斯“福布斯”搭载的“萤火一号”因火箭原因失败后，我国将独立开展火星探测研究。

目前对火星探测器通常由深空网利用无线电信号对探测器进行测量，测量元素包括测距和多普勒测速，还可辅助以VLBI测量，测量元素为时延、时延率或地心惯性系赤经、赤纬［2－3］。其中，VLBI能补充地面测站视线法向方向上的观测，对仅用地面无线电测量的精度会有显著的改进［4］。中国VLBI网(CVN)对欧空局火星快车进行了数次跟踪观测，对时延、时延率定位效果进行了分析，当时延精度为2ns～5ns时，火星快车卫星的定位精度约为0.1as［5］。无线电测量和 VLBI测量都是相对地心的，在巡航段，由于距离远，偏心率大，引力约束小，测量数据的微小误差就能引起定轨预报的较大误差［6］。如果火星探测器配备有光学照相机跟踪目标天体中心，就可以得到目标天体相对探测器的视线信息。由于该信息为相对目标天体的角度信息，能够精确地确定目标天体垂直视线方向上的探测器状态，因此可以结合地面无线电测量数据与星载光学测量数据进行融合定轨，从而提高探测器定轨预报精度。

1 组合导航定轨算法

在历元(J2000.0)火星质心局部坐标系中，探测器运动方程为［7］

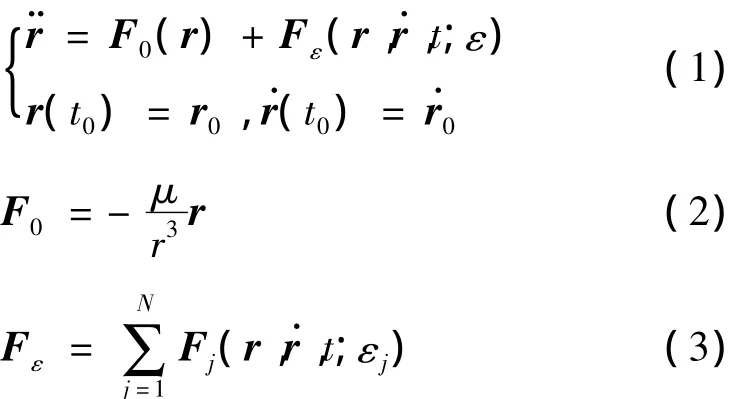
其中，μ为火星引力常数;F0为二体问题下火星对探测器的引力加速度;Fε为各种摄动源共同作用下的摄动加速度;r为探测器的火星质心位置矢量;˙r为探测器的火星质心速度矢量;¨r为探测器的火星质心加速度矢量。摄动力包括火星非球形引力摄动、地球引力摄动、太阳引力摄动、太阳光压摄动和火星物理天平动。火星上存在大气，但在巡航段，探测器离火星距离很远，大气阻尼作用可以不考虑。

待估历元记为t0，相应的待估状态量记为X0，利用一列采样数据 tj，Yj(j=1，2，…，N)，进行批处理定轨，就可得到历元时刻的状态向量为:

其中，y为残差，B为相应的(m×n)维法化矩阵;m为n次采样数据对应的维数;n则为待估状态量维数，W为加权矩阵。

在火星探测器定轨过程中，用到的时间标准包括 TAI，UTC，UT1，TDB，TT，TDT，坐标系包括太阳系质心坐标系、地心局部坐标系、地固坐标系、火星质心局部坐标系、火心固定坐标系等。坐标系转换要用JPL/NASA发布的行星历表，目前推荐使用DE421，所用时间标准为TDB。

对于无线电测量，需要把卫星在火心J2000惯性坐标系中t时刻的状态矢量转换成地球固定坐标系的状态矢量，修正潮汐对观测站站址的影响，然后把卫星在地球固定坐标系中的状态矢量转换到测站坐标系中，计算测距和距离变化率及其对位置速度的偏导数。而光学照相机采集的数据，是基于火星坐标系下的，可以将图像下传至地面进行处理，通过反复迭代计算得到探测器在火星J2000坐标系下的视线方向，相当于t时刻火星J2000惯性坐标系下的赤经、赤纬α，δ，而VLBI测量中赤经赤纬是在地心J2000坐标系下定义的［5］。光学测量赤经α在火星J2000坐标系中按顺时针方向从X轴(春分点方向)起量，其数值范围为0～2π，δ从Z轴起量，取值范围为(－π/2～π/2)。

由卫星在火星惯性中位置矢量σ可得赤经α的计算值:

计算中应根据x和y的符号判定赤经α的象限。赤经α、赤纬δ对火星惯性系卫星状态矢量σ的偏导数:

2 无线电定轨精度分析

设计一条从地球到火星的轨道，选取近火点前约14天的历元轨道参数，见表1。仿真生成我国两个深空探测站的测距、测速数据。两个深空探测站分别位于喀什和佳木斯，经度差约55°，纬度上都在北纬40°左右。仿真时考虑了一个最优指标:测距系统差为2m，随机差为1m，测速系统差为2cm/s，随机差为1cm/s。另外，还考虑了一个日常指标，即测距系统差为5m，随机差为5m，测速系统差为5cm/s，随机差为5cm/s。仿真结果表明，无线电测量每天可跟踪弧段为13小时左右。

表1 转移轨道段轨道参数Table 1 Orbit elements for mars detector during cruise phase

分别采用3天、7天、10天数据定轨，预报到近火点时刻，预报时间分别为11天，7天和4天。在定轨过程分别考虑三种情况:只考虑随机差，不考虑系统差和动力学模型误差(面质比为0.005，10%的光压反射系数，下同);考虑随机差和系统差，不考虑动力学模型误差;随机差、系统差和动力学模型误差都考虑。各种情况下的定轨预报误差如表2所示。实际的观测数据与仿真数据相比，随机性略差，系统误差和模型误差的具体大小难以确定，所以第一种情况则反映了定轨的理想精度，而第三种情况则反映实际中较差的定轨预报精度。从表中可以看出:在深空探测轨道确定中，最重要的误差来源于光压摄动，这从其它文献也可以得出类似的结论［5］，在不考虑光压模型误差的情况下，高精度测量轨道确定精度能够达到千米量级，预报10天位置误差达到数十千米量级，如果考虑10%的光压模型误差，则导致定轨预报位置误差急剧恶化;如果光压模型误差较大，并不是定轨弧段越长，定轨预报精度就越高，这是由于光压系数约束松，往往出现不切实际的过大或过小，从而导致长弧定轨滤波发散［8］;由于火星引力作用，近火点附近预报误差有可能小于定轨误差。随机差和系统差越大，定轨精度越差，但是并不成简单比例。

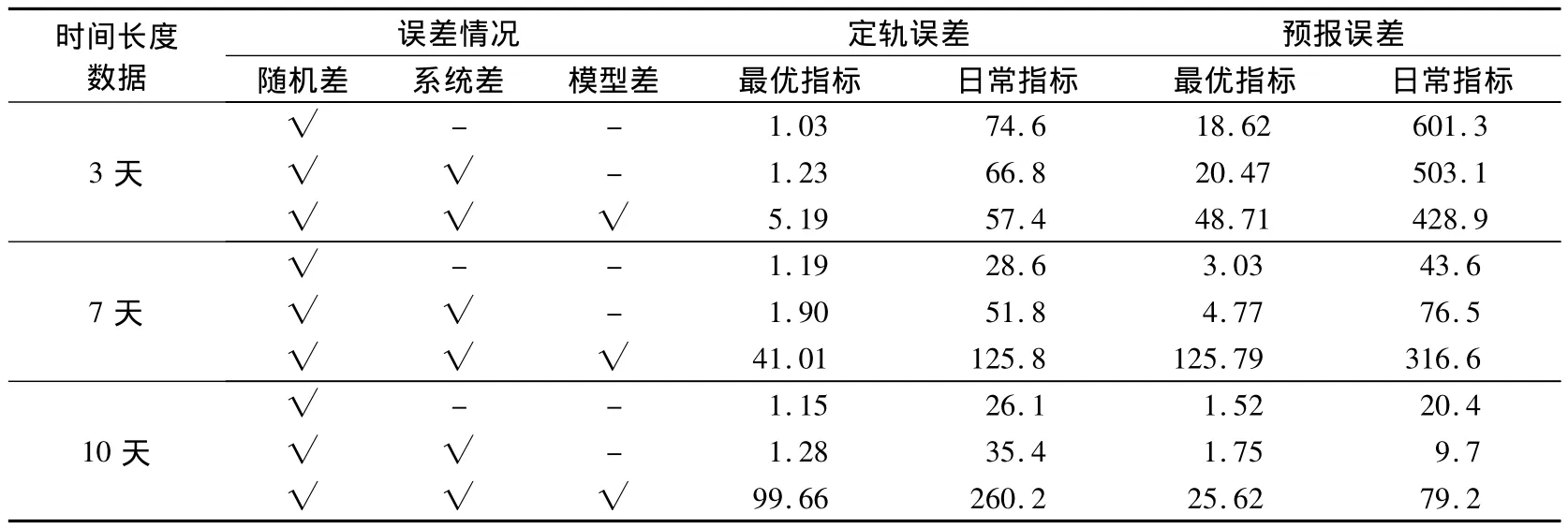
表2 无线电测量下的定轨预报误差(单位:km)Table 2 The error of orbit determination and prediction with radio measurement(unit:km)

3 组合导航定轨精度分析

对于火星巡航段的光学测量，基本上是全天候可见，如图1，然而在近火点前的15天内，探测器近似一条直线飞向火星，所以赤经赤纬的变化不明显，每日变化范围不足1as，所以光学测量相对位置的变化不够敏感。如果无线电测量能够达到测距系统差为2m，随机差为1m，测速系统差为2cm/s，随机差为1cm/s的指标，增加随机差为5as的光学测量数据定轨，其定轨预报误差见表3。可见，如果无线电测量精度较高，增加5as的光学测量数据后，定轨预报精度是否提高，取决于定轨过程中模型误差的大小。如果模型误差较大，则利用随机差为5as的光学测量数据，定轨预报精度明显提高。如果模型误差较大，则定轨预报精度改善不明显，甚至有可能更差。

通常，无线电测量精度很难达到理想的精度，目前深空探测中的测距系统差约为5m，随机差约为5m，测速系统差为5cm/s，随机差为5cm/s，，如果光学测量随机差为10as，系统差分别为0as、10as、5as和2as，则定轨预报误差见表4，可见，增加随机差为10as的光学测量数据后，定轨精度是否改善，取决于光学测量的系统误差，如果光学测量包含2as的系统差，则定轨精度和预报精度都有明显提高，系统误差每减小1as，定轨误差提高10km左右。

表3 最优指标无线电测量下的组合导航误差(单位:km)Table 3 The integrated navigation error with the optional radio measurement(unit:km)

表4 日常指标无线电测量下的组合导航误差(单位:km)Table 4 The integrated navigation error with the normal radio measurement(unit:km)

图1 火星J2000坐标系下的探测器赤经赤纬测量(横轴:小时)Fig.1 The right ascension and declination measurement in Mars-centered J2000 frame(x-axis:hour)

如果光学照相机的目标由火星改为火卫1和火卫2，则由于火卫1和火卫2，环绕火星运转，跟踪几何有所改善，定轨精度有所提高，尤其是半长轴大的火卫2，提高更加明显。但跟踪几何导致的精度改善与系统差提高对精度改善相比，仍然差一个量级，并且随着定轨的弧段离火星越近，跟踪几何改善更好，定轨精度改善越明显。

4 不同系统差方向组合导航精度分析

仿真生成测距随机差、系统差为5m，测速随机差、系统差为5cm/s的扩频无线电测量数据，数据采样点为5秒1点。面质比为0.01，定轨时考虑10%的光压模型误差，采用3天数据定轨，预报10天，定轨预报误差见表5所示。其中定轨最大误差为20km，预报最大误差为120km。仿真生成光学测量数据，采样点同样为5秒1点，随机差为1as。系统差分别为 0.2as，0.5as 和 1as。由于实际测量中，系统差的方向有可能是正值，也可能是负值。为了搞清楚不同方向系统差对定轨预报的影响，我们仿真了光学测量赤经赤纬数据不同组合的数据进行定轨，结果见表5。从表中可见，联合定轨中对于不同方向但大小一样的光学测量数据，定轨的总误差基本上一致，但是R、T、N三个方向上的误差不一样。另外，由于不同方向的误差预报中发散程度不同，导致预报误差也不一致，从几千米到几十千米不等。

另外，我们针对不同测量弧长和测量频率的光学数据和无线电数据联合定轨的结果，可以得出光学数据越稀，定轨精度越差，预报精度也会变差，所以建议数据采集尽可能得密，至少为10分钟1点，测量弧长至少为24小时以上。针对较近距离300万千米以及较远距离1 000万千米的轨道进行仿真，利用无线电数据和光学数据联合定轨，可以得出距离火星越近，光学测量对组合导航的定轨预报精度改善更好的结论，即使在1 000万千米，光学测量仍然对定轨预报精度有改善。

5 结论

火星探测器在巡航段，光压不确定性是影响定轨预报精度的重要因素，如果采用高精度的无线电测量，系统差和随机差控制在1m左右，则定轨精度能够达到千米量级，10天左右的预报误差为几十千米。如果系统差和随机差在5m左右，则定轨精度能够达到几十千米量级，10天以内的预报误差达到几百千米。对于高精度无线电测量，测距系统差为2m，随机差为1m，测速系统差为2cm/s，随机差为1cm/s，增加5as的光学测量数据后，定轨预报精度是否提高，取决于定轨过程中模型误差的大小。对于中精度无线电测量，增加随机差为10as的光学测量数据后，测距系统差为5m，随机差为5m，测速系统差为5cm/s，随机差为5cm/s，定轨精度是否改善，取决于光学测量的系统误差大小，系统误差每减小1as，定轨误差提高10km左右。光学测量的系统差相同，方向不同，影响定轨误差的方向，但对定轨误差的大小影响不大，对于长时间的预报精度影响较大，但不改变预报误差的大致量级。分别针对距离火星300万千米和1 000万千米的轨道进行仿真，可以得出距离火星越近，光学测量对组合导航的定轨预报精度改善更好的结论。

［1］ 黄勇，胡小工，曹建峰，等.上海天文台火星卫星定轨软件系统［J］.飞行器测控学报，2009，28(6):83－89.［Huang Yong，Hu Xiao-gong，Cao Jian-feng，et al.The Mars satellite orbit determination software at Shanghai astronomical observatory［J］.Journal of Spacecraft TT ＆ CTechnology，2009，28(6):83－ 89.］

［2］ 郑为民，舒逢春，张冬.应用于深空跟踪测量的VLBI相关处理技术［J］.宇航学报，2008，29(1):18－23.［Zhen Weiming，Xu Feng-chun， Zhang Dong. Application of software correlator to deep space VLBI tracking［J］. Journal of Astronautics，2008，29(1):18 －23.］

［3］ 鄢建国，李斐，平劲松.基于MGS测图段部分弧段的精密定轨及火星重力场模型解算［J］.测绘学报，2010，39(5):484－490.［Yan Jian-guo ，LI Fei，Ping Jin-song.Precision orbit determina tion of MGS mapping phase arcs and Mar tian gravity field model solution［J］.Acta Geodaetica et Cartographica Sinica，2010，39(5):484 －490.］

［4］ 曹健峰，黄勇，胡小工，等.利用中国VLBI网实现对“火星快车”的测定轨［J］.科学通报，2010，55(28):2659－2666.［Cao Jian-feng，Huang Yong，Hu Xiao-gong，et al.Mars express tracking and orbit determination trials with Chinese VLBI network［J］.Chinese Sci.Bull，2010.55(28):2659 －2666.］

［5］ 李金岭，刘鹂，马茂莉，等.中国VLBI网火星快车卫星跟踪资料的定位归算［J］.宇航学报，2010，31(7):1718 －1723.［Li Jin-ling，Liu Li，Ma Mao-li，et al.Positioning reduction of the Mars express tracking data by the Chinese VLBI network［J］.Journal of Astronautics，2010，31(7):1718 －1723.］

［6］ Antreasian P G，Baird D T，Border JS，et a1.2001 Mars odyssey orbit determination during interplanetary cruise［J］.Journal of Spacecraft and Rockets，2005，42(3):394 －405.

［7］ 李济生.人造卫星精密轨道确定［M］.北京:解放军出版社，1995:41－54.

［8］ 李杰，郑勇.火星探测器行星际定轨中处理光压模型误差的两种定轨方案之比较［J］.深空探测研究，2011，9(2):8－11.［Li Jie，Zheng Yong.Comparison of two filter strategies for Mars probe interplanetary orbit determination［J］.Deep Space Exploration，2011，9(2):8 －11.］