近震S波震相实时自动识别方法研究

曲保安 刘希强 蔡 寅， 范晓勇 林秀娜于庆民 赵 瑞 李 铂 周彦文

1）中国山东泰安271000山东省地震局泰安基准地震台

2）中国山东济南250014山东省地震局

3）中国北京100081中国地震局地球物理研究所

引言

随着数字地震观测资料应用的日益广泛和深入，地震学者对震相自动识别技术日趋关注，震相自动识别在海量资料分析和实时资料处理等领域得到了较快的发展.

1976年，Stevenson发表了其在地震自动分析方面的研究成果，其方法核心即为长短时平均能量比（short term average／long term average，简写为STA／LTA）（Stevenson，1976）.次年Stewart（1977）提出了用于近震实时检测和定位的方法.1978年，Allen发表了应用单通道地震记录进行地震自动检测和到时识别的文章（Allen，1978）.1982年，Allen又对当时震相自动识别的应用现状和未来发展进行了总结和展望，同时提出了用特征函数作为输入参数的STA／LTA算法（Allen，1982）.该特征函数思想经过不断发展目前仍在广泛应用（李山有等，2006；高淑芳等，2008）.迄今，经过30多年的发展，各种新的震相自动识别算法随着数字信号处理技术、概率论以及自动控制理论的发展被广泛提出和应用.我们将震相自动识别分为3步.第一步：预处理.是对原始信号进行各种滤波和时频转换，包括傅里叶变换、Gaber变换、Wigner-Ville分布、小波变换、小波包变换、Hilbert-Huang变换等预处理算法（刘希强等，1998，2000，2002；杨配新等，2004；Granet，1983）.第二步：震相识别算法.又可分为能量成分算法（如STA／LTA算法）、频率成分算法（如瞬时频率算法）、波形算法（如AIC算法）、波动矢量差异算法（如偏斜角）和动态特征算法（如偏振分析、线性度、功率谱和频谱）等5部分（Roberts et al，1989）.第三步：方法综合判定.对第二步的算法进行各种组合和阈值设定，并依据各种情形确定相应的识别程序及方法，包括后期的用人工神经网络对判定方法进行训练（Baer，Kradolfer，1987）.经过上述3步的震相自动识别方法在P波震相识别方面得到了广泛的应用，并取得了良好的效果.但是在S波自动识别方面，由于P波尾波以及各种反射震相，如PmP的强干扰，STA／LTA算法用于S波震相自动识别的效果较差，Roberts等（1989）基于S波与P波质点振动方向的差异，提出了用偏振分析方法识别S波.Cichowicz（1993）提出了采用偏斜角、偏振度和切向能量与总能量比值3种参数相乘得到的值作为判断依据的方法，该方法总有效性达到65%—70%.Bai和Kennett（2000）采用能量分析、自回归表征和瞬时频率技术并与偏振分析结合进行综合震相识别，此方法对震中距17.3°—41.6°的各种远震震相的识别能力较高，包括远震S波震相识别，但用于近震识别S波震相识别精度较低.Diehl等（2009）提出了用于地震层析成像的S波自动识别方法，该方法需经过STA／LTA判定、偏振分析、坐标系变换、自回归Akaike信息准则（auto regressive-Akaike information criterion，简写为AR-AIC）等一系列综合判定，计算量较大，可用于资料的后续分析.经过对2 500个S波震相识别结果与人工分析结果比较，该方法最大误差大约为0.27s.Amoroso（2012）对台网资料后续分析的S波自动识别采用了偏振滤波与波形一致性方法.Kuperkoch等（2012）采用波形自回归预测方法，对地方震、近震和远震的S波进行了自动判定，识别的平均误差为0.5s±0.8s.

本文旨在研究根据实时地震波形进行地震早期预警方面的快速S波震相识别.依据马强（2008）的地震预警动态定位的6种情形，S波到时圆包含地震预警动态定位的重要信息，对S波进行识别是地震预警动态定位的必要环节.本文尝试性地提出一种S波自动识别的方法，秉承“滤波越少，算法越好”（“the less filtering，the better the algorithm”）的思想（Douglas，1997），对原始三分向记录波形不做任何滤波处理，由于已知由其它自动识别方法得到的P波到时，从而对S波到时可进行快速自动高精度的识别.对于P波的精确识别，推荐采用刘希强等（2009）的三阶统计Akaike信息准则（three order cumulative-Akaike information criterion，简写为TOC-AIC）方法.

1 识别方法

本文方法的基本思路是根据由其它方法自动识别的P波的动态特征，求得波形的波动矢量，即P波的质点振动方向，并选取计算窗长对后续波形进行质点振动方向滑动计算，求得后续波形质点振动方向与P波质点振动方向的夹角，即偏斜角；将偏斜角和水平能量占总能量的比值的平方积作为确定识别区间的依据；然后根据方差Akaike信息准则（variance-Akaike information criterion，简写为VAR-AIC）判定两个水平分向S波初动位置，并对两个水平分向各自的识别结果进行分析判断，确定S波震相到时.

1.1 确定窗长

鉴于震中距小于100km的地方震，其P波的周期约为0.05—0.2s，S波的周期约为0.1—0.5s（朱元清等，2002）.根据山东省地震台网密度，以及Nyquist采样定理，选取P波到时之后0.5s的波形数据，计算P波的卓越频率（Boore，1983；Andrews，1986）

式中，fP为P波卓越频率，m1和m2计算公式为

式中，v2（f）和D2（f）分别为速度功率谱密度和相应的位移功率谱密度.将fP／2作为S波的卓越频率，计算窗长

式中，fS为采样率，lw为计算波形偏振方向的窗长.

鉴于本研究所用资料为山东数字地震台网记录的数据，为速度记录，所以在计算m2之前要将速度记录仿真为位移记录.本文采用的数值积分方法为Newton-Cotes求积算法

从计算精度和计算量两方面综合分析，本文选择n＝4时的Newton-Cotes公式

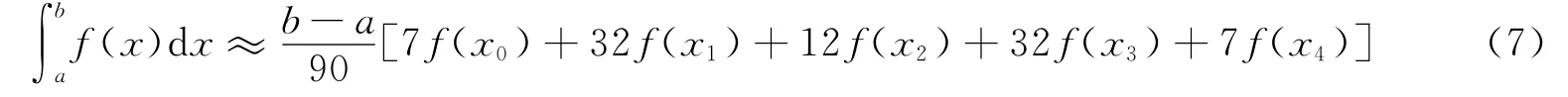
该计算结果具有5次代数精度，其截断误差为

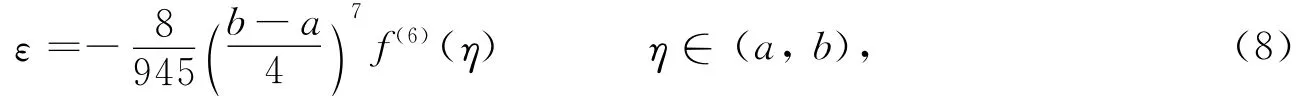
同时，对窗长进行限定，大于采样率的1／5，小于采样率的一半（即Nyquist频率）.

1.2 计算偏斜角

选取P波之后lw长度的数据计算其最大特征值对应的特征向量，即P波的偏振方向（质点振动方向），单台三分向lw长度的数据协方差矩阵为

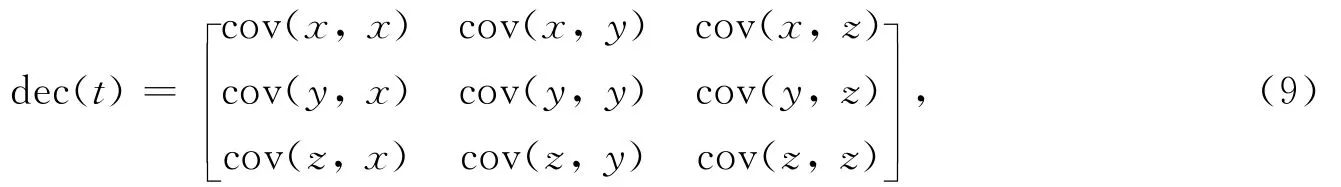
长度为lw的任意两组变量x和y的协方差为

从lw长度之后开始进行逐点滑动，求得各个数据窗最大特征值对应的特征向量，并计算与P波偏振方向的夹角.

1.3 水平能量与总能量比值

水平能量与总能量比值，即窗内两个水平分向能量和与三分向能量和的比值，计算公式为

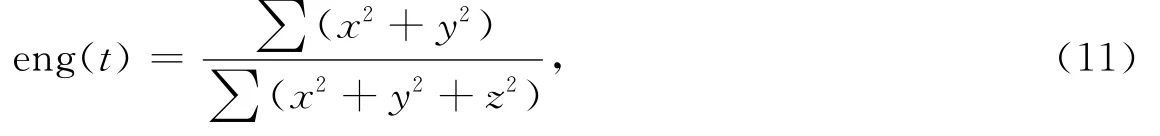
式中，x和y为两个水平分向波形数据序列，z为垂直分向波形数据序列.

1.4 VAR-AIC

Maeda（1985）提出了直接根据地震图记录而得到AIC函数的方法，称为VAR-AIC方法.AIC函数的最小值对应的时间就是地震震相初至.AIC函数表示为

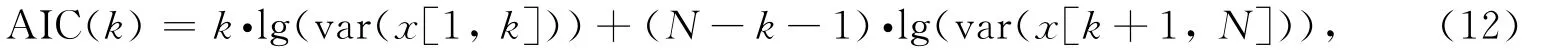
式中，var（x［1，k］）和（var（x［k＋1，N］）分别表示两个时间段内数据的方差.

1.5 判定标准

对于S波的初步判定，选取偏斜角和水平能量与总能量比值的平方积作为特征函数（cf），即

阈值选择自P波开始至计算点位置的均值的5倍加方差的5倍.以此特征函数作为判定S波识别区间的判据，对S波进行初步判定.之后选取初判位置前3个lw长度和后3个lw长度的数据作为精确判定的区间，采用VAR-AIC方法分别对NS和EW分向进行S波的精确识别.对于识别的两个分向各自的S波位置，如果时间差小于0.1s，则认为二者的差值是由于S波分裂造成，则取二者的平均值作为识别的S波位置；如果二者的差值大于0.1s，则认为某一个分向存在误识别，分别计算两个分向各自的识别位置前后lw长度信号的信噪比，取信噪比较大的一个分向的判定结果作为S波的识别位置.

2 资料和结果分析

结合山东数字地震台网记录的数据，将本文震相识别方法的结果与人机交互处理结果进行对比，最后确定其有效性.

按照震级不同选取29个地震事件，每个地震事件选择震中距100km范围内的台站记录，要求记录可以精确识别P波到时，共选取56个台站的118个三分向记录.通过这118个三分向记录波形对本文方法进行了测试.本研究所涉及的地震及台站分布见图1.本文所选取的地震事件参数见表1.地震选取考虑以下3方面：① 信噪比随震级的变化；② 信噪比随震中距变化；③ 信噪比受台站背景噪声及地震射线传播路径影响.此方法统筹同一台站对不同震级地震的识别能力，又兼顾全省台站各自背景噪声的不同，从而在全省不同位置选取地震事件，同时也在相近震中位置选取不同震级的事件（烟台莱州震群和濮阳范县附近4次不同震级地震）.

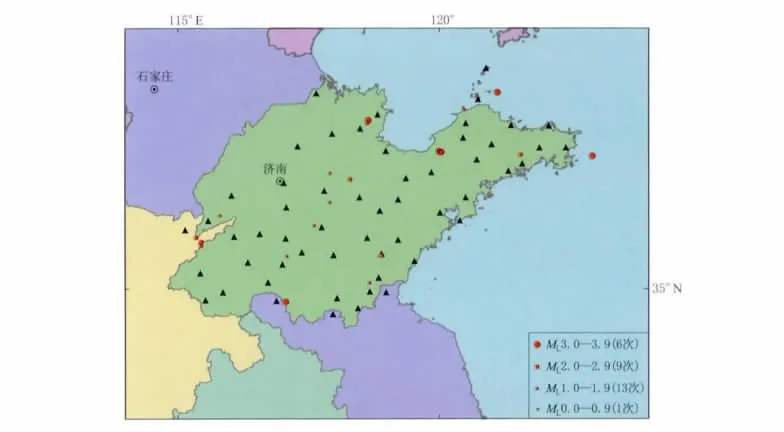
图1 本研究涉及的地震震中和台站分布图实心三角形表示台站，实心圆形表示地震震中位置Fig.1 Distribution of earthquakes and stations used in this studySolid triangles denote seismic stations，solid circles denote the epicenters of earthquake

表1 本文所选取的地震事件参数Table 1 Detailed information of selected earthquake events

为了体现该方法的实时性，在对三分向记录进行S波识别时，采用与现有Jopens系统类似的方法，将三分向数据以数据包形式分割发送，每秒1个包，模拟从数采实时获取数据.

图2为118个三分向记录的自动识别结果与人机交互识别结果的对比，即以人机交互结果为标准，自动识别结果的误差分布图.图中横轴为二者的差值，纵轴为S波对P波尾波的信噪比.对118个三分向记录的识别结果按照S波对P波尾波的信噪比不同进行了统计（表2）.对于误差大于0.1s的震相识别作为无效识别.本文所采用的118个三分向记录，其信噪比均小于12.最高信噪比为11.56，最低信噪比为－2.28.

如表2所示，本文所提出的S波实时自动识别方法对于信噪比大于5的地震事件，按照识别误差小于0.1s的精度要求，识别有效率高达89.39%，有效识别平均误差为0.05s.对于低信噪比大于0小于5的三分向地震记录，按照识别误差小于0.1s的精度要求，识别有效率达到65.79%，有效识别平均误差为0.07s.综上，本文识别方法在信噪比相对较低的情况下能够实现较高的有效率和较小的识别误差.

图2 118个三分向记录的自动识别结果与人工交互识别结果对比Fig.2 Comparison between automatic identification results and human-computer interaction recognition results for the 118three-component records

表2 识别结果统计Table 2 Statistics on identification results

3 讨论与结论

本文提出了一种用于地震早期预警的S波震相实时自动识别方法.该方法不对原始信号进行任何滤波处理，直接根据偏斜角和水平能量与总能量比值确定识别区间；采用VAR-AIC方法对两个水平分向分别进行精确识别；对两个识别结果进行判断，确定S波初动时刻.

经过对118个三分向记录的实际应用验证，本文方法具有识别有效率高、识别误差小的优点.由于P波尾波以及各种反射震相的强干扰，S波的信噪比整体偏低，不利于S波有效识别及识别精度的提高.本文方法对于信噪比大于5的地震记录可以实现S波震相高精度的实时有效识别.虽然与目前已有的P波0.02s的识别精度还有一定差距，但0.1s的识别误差小于Amoroso等（2012）和Kuperkoch等（2012）的识别误差，而且本方法识别有效率高达89.39%.

本文方法是在基于P波已经由其它方法精确识别的基础上提出的.其P波卓越频率、窗长及P波偏振方向的计算均受P波的识别精度影响，但是鉴于目前P波识别精度已达到0.02s，而且本文选择窗长为0.5s，故本方法能够达到较高的识别精度.

高淑芳，李山有，武东坡，马强.2008.一种改进的STA／LTA震相自动识别方法［J］.世界地震工程，24（2）：37－－41.

Gao S F，Li S Y，Wu D P，Ma Q.2008.An automatic identification method of seismic phase based on modified STA／LTA algorithm［J］.World Earthquake Engineering，24（2）：37－－41（in Chinese）.

李山有，朱海燕，武东坡，宋晋东.2006.基于振幅和瞬时频率的震相自动识别方法［J］.世界地震工程，22（4）：1－－4.

Li S Y，Zhu H Y，Wu D P，Song J D.2006.Automatic recognition of seismic phase based on amplitude and instantaneous frequency［J］.World Earthquake Engineering，22（4）：1－－4（in Chinese）.

刘希强，周蕙兰，郑治真，沈萍，杨选辉，马延路.1998.基于小波包变换的弱震相识别方法［J］.地震学报，20（4）：373－－380.

Liu X Q，Zhou H L，Zheng Z Z，Shen P，Yang X H，Ma Y L.1998.Identification method of weak seismic phases on the basis of wavelet packet transform［J］.Acta Seismologica Sinica，20（4）：373－－380（in Chinese）.

刘希强，周蕙兰，沈萍，杨选辉，马延路，李红.2000.用于三分向记录震相识别的小波变换方法［J］.地震学报，22（2）：125－－131.

Liu X Q，Zhou H L，Shen P，Yang X H，Ma Y L，Li H.2000.Identification method of seismic phase in three-component seismograms on the basis of wavelet transform［J］.Acta Seismologica Sinica，22（2）：125－－131（in Chinese）.

刘希强，周蕙兰，曹文海，李红，李永红，季爱东.2002.高斯线调频小波变换及其在地震震相识别中的应用［J］.地震学报，24（6）：607－－616.

Liu X Q，Zhou H L，Cao W H，Li H，Li Y H，Ji A D.2002.Gauss linear frequency modulation wavelet transform and its application to seismic phase identification［J］.Acta Seismologica Sinica，24（6）：607－－616（in Chinese）.

刘希强，周彦文，曲均浩，石玉燕，李铂.2009.应用单台垂向记录进行区域地震事件实时检测和直达P波初动自动识别［J］.地震学报，31（3）：260－－271.

Liu X Q，Zhou Y W，Qu J H，Shi Y Y，Li B.2009.Real-time detection of regional events and automatic P-phase identification from the vertical component of a single station record［J］.Acta Seismologica Sinica，31（3）：260－－271（in Chinese）.

马强.2008.地震预警技术研究及应用［D］.哈尔滨：中国地震局工程力学研究所：40－－46.

Ma Q.2008.Study and Application on Earthquake Early Warning［D］.Harbin：Institute of Engineering Mechanics，China Earthquake Administration：40－－46（in Chinese）.

杨配新，邓存华，刘希强，任勇，颜其中.2004.数字化地震记录震相自动识别的方法研究［J］.地震研究，27（4）：308－－313.

Yang P X，Deng C H，Liu X Q，Ren Y，Yan Q Z.2004.Studies on auto-distinguishing phase of digital seismic recording［J］.Journal of Seismological Research，27（4）：308－－313（in Chinese）.

朱元清，佟玉霞，于海英，宋俊高.2002.数字化台网的近震震相自动识别［J］.西北地震学报，24（1）：5－－12.

Zhu Y Q，Tong Y X，Yu H Y，Song J G.2002.Automatic recognition of seismic phases of regional earthquake［J］.Northwestern Seismological Journal，24（1）：5－－12（in Chinese）.

Allen R V.1978.Automatic earthquake recognition and timing from single trace［J］.Bull Seismol Soc Am，68（5）：1521－－1532.Allen R V.1982.Automatic phase pickers：Their present use and future prospects［J］.Bull Seismol Soc Am，72（6B）：225－－242.

Amoroso O，Maercklin N，Zollo A.2012.S-wave identification by polarization filtering and waveform coherence analyses［J］.Bull Seismol Soc Am，102（2）：854－－861.

Andrews D J.1986.Objective determination of source parameters and similarity of earthquakes of different size［M］∥Das S，Boatwright J，Scholz C eds.Earthquake Source Mechanics.Washington D C：American Geophysical Union：20－－23.

Bai C Y，Kennett B L N.2000.Automatic phase detection and identification by full use of single three-component broadband seismogram［J］.Bull Seismol Soc Am，90（1）：187－－198.

Baer M，Kradolfer U.1987.An automatic phase picker for local and teleseismic events［J］.Bull Seismol Soc Am，77（4）：1437－－1445.

Boore D M.1983.Stochastic simulation of high-frequency ground motions based on seismological models of the radiated spectra［J］.Bull Seismol Soc Am，73（6A）：1865－－1894.

Cichowiez A.1993.An automatic S-phase picker［J］.Bull Seismol Soc Am，83（1）：180－－189.

Diehl T，Deichmann N，Kissling E，Husen S.2009.Automatic S-wave picker for local earthquake tomography［J］.Bull Seismol Soc Am，99（3）：1906－－1920.

Douglas A.1997.Bandpass filtering to reduce noise on seismograms：Is there a better way？［J］.Bull Seismol Soc Am，87（3）：770－－777.

Granet M.1983.An automatic seismic signal detection based on linear prediction filter theory［J］.Ann Geophys，1：109－－114.Kuperkoch L，Meier T，Brustle A，Lee J，Friederich W，EGELADOS Working Group.2012.Automated determination of S-phase arrival times using autoregressive prediction：Application to local and regional distances［J］.Geophys J Inter，188（2）：687－－702.

Maeda N.1985.A method for reading and checking phase times in autoprocessing system of seismic wave data［J］.Zisin，38（6）：365－－379.

Roberts R G，Christoffersson A，Cassidy F.1989.Real-time event detection，phase identification and source location estimation using single station three-component seismic data［J］.Geophys J Int，97（3）：471－－480.

Stevenson P R.1976.Microearthquakes at Flathead Lake，Montana：A study using automatic earthquake processing［J］.Bull Seismol Soc Am，66（1）：61－－80.

Stewart S W.1977.Real-time detection and location of local seismic events in central California［J］.Bull Seismol Soc Am，67（2）：433－－452.