震后形变和岩石圈流变学结构
刘绍卓 沈正康
1)中国北京100029中国地震局地质研究所地震动力学国家重点实验室
2)中国北京100871北京大学地球与空间科学学院
引言
岩石圈流变学结构是地学研究的重要内容之一,几乎所有时间和空间尺度下发生的地质构造运动都与岩石圈流变学结构直接相关(Flemings,Jordan,1990;Buck,1991).人们通常借助于间接的地球物理观测和理论推估(Bodine et al,1981),或者是直接的室内岩石力学实验模拟(Kirby,Kronenberg,1987)获得对岩石圈流变学结构特征的认识.随着空间大地测量观测技术的发展,利用震后形变观测资料约束岩石圈流变学结构和断裂带内的力学性质成为地球动力学的研究热点之一(Shen et al,1994;Pollitz et al,2000),众多研究深化了人们对各个区域的岩石圈流变学结构的认识.然而震后形变研究不应将其视为一个独立的地震学和地球动力学研究方向,而应该从整体大地学背景下综合考虑其研究意义.作为发生在岩石圈内部的地球物理现象,空间大地测量所观测到的震后形变效应与该区域的岩石圈流变学结构以及断裂带内力学性质密切相关,而这种流变学结构又与宏观的区域地质构造演化史相关.在微观机制方面,岩石力学实验为岩石圈内不同深度的岩石流变学特征提供了宝贵的约束.故对岩石圈流变学结构的完整认识应当包括对过去发生的地质构造演化史的分析,重视现今的地球物理观测,以室内实验获得的岩石力学规律为依据,从宏观和微观两方面综合分析建模等,以获得更为合理的解释.本文将从岩石力学角度阐述震后形变的研究背景,并以美国南加州1992年Landers MW7.3地震和1999年Hector Mine MW7.1地震震后形变研究为具体案例,总结该领域的研究进展,最后对大陆岩石圈流变学结构研究做简要概述.
1 构造物理实验研究背景
目前主要有两大类岩石力学实验(摩擦实验和流变学实验)试图从微观角度解释地震周期内的各种现象,本节将对这两类实验的相关成果加以简要阐述.
1.1 摩擦实验
地震是发生在先存断层上的非稳态黏滑而不是纯粹的宏观破裂(Brace,Byerlee,1966),因为后者的应力降显著高于实际地震的应力降.断层的失稳黏滑由断层面上的摩擦强度确定,摩擦强度通常由Byerlee准则(公式(1))来描述(Byerlee,1978).公式(1)表示具有一定内聚力c和摩擦系数μ的断层面在有效正应力¯σ和剪切力τ作用下断层面上的摩擦力大小.在Byerlee准则中,剪切力等效于摩擦力,即

然而,后期的研究却发现断层面上的地震行为与脆性摩擦速率及状态相关(Dieterich,1978,1994;Ruina,1983;Scholz,1998).基于这类岩石力学摩擦模型,摩擦分为静摩擦和动摩擦,摩擦系数由断层面上接触体的接触时间、位移和速度效应控制(Dieterich,1972,1978,1979).静摩擦系数随着凹凸体静态接触时间的增长而增加,动摩擦系数受控于特征位移和滑动速率.此外,瞬态的速率增加会造成摩擦系数的瞬态增加(Dieterich,1979).对于一维的弹簧-滑块模型,如果对系统施加一个小的位移扰动,弹簧内积累的应力超过滑块与地面之间的摩擦力,就会发生黏滑.黏滑的发生依赖于施加在系统上的正应力、系统的刚度和接触面的粗糙程度.高的正应力、软的系统和较光滑的接触面更利于发生黏滑(Dieterich,1978).综合这些因素可以得到经验性的速率-状态摩擦准则,准则中包括滑动速率和滑动状态等参量 (Ruina,1983;Dieterich,1994).著名的Ruina-Dieterich准则可用下式表示(Scholz,1998):

式中,τ和¯σ分别为切应力和有效正应力;V和V0分别为滑动速率和参考滑动速率;μ0为相应于参考滑动速率对应的摩擦系数;a和b为经验常数;Dc为特征位移;θ为状态变量,与时间同量纲并随时间变化.对于考虑有效正应力的稳态摩擦可以表示为

式中,(a-b)为负值意味着系统具有速率弱化特征,系统易发生非稳态滑移,在低有效正应力的情况下,准静态加载使得系统发生稳态滑移,动态加载则使系统发生非稳态滑移;(a-b)为正值意味着系统始终发生稳态滑移.速率-状态摩擦准则可以解释很多观测到的摩擦滑动现象和实际地震断层活动现象.然而,Dieterich类摩擦模型在现代材料科学背景下却显得比较初级,因为速率-状态相依的摩擦可以由诸多不同尺度下的微观机制解释,而不仅仅局限于Dieterich类摩擦模型依赖的摩擦和愈合机制.在矿物颗粒边界或者内部,或在滑动接触面上,或在固体凹凸体内部,都有可能用所发生的机制来解释速率-状态相依的摩擦现象.最新的研究进展表明,盐的稳态摩擦现象可以由颗粒内部行为占主导并伴随颗粒边界行为来解释 (Niemeijer,Spiers,2007).
1.2 流变学实验
实验室条件下岩石的蠕变特征在某种程度上与地表的震后形变时间演化特征具有类似性,但因二者所处的环境和物质组成差别太大,其背后的机制并不一定相同.在恒定应力加载的岩石蠕变实验中,在一定的观测时间内,岩石的力学响应表现为初始的瞬态蠕变和紧邻发生的稳态蠕变.在发生疲劳屈服之前,因稳态蠕变所调整的应变量显著高于瞬态蠕变所调整的应变量,岩石实验主要研究稳态蠕变的微观力学机制和构建合理的本构关系.目前有关瞬态蠕变机制的研究还较少.
稳态蠕变主要有两种微观机制解释:晶内(体)塑性变形和扩散蠕变(Weertman,1955,1970).晶内塑性变形主要由晶内缺陷的运动(位错)造成,稳态晶体蠕变(恢复位错蠕变)当且仅当做功强化和恢复过程达到平衡时才发生.这两类位错运动负责两类矛盾的过程,位错滑移造成做功强化,位错攀移和交叉滑移又导致恢复过程.扩散蠕变主要是因颗粒周缘的加载应力差造成的物质流动而产生的颗粒变形,常常伴随着颗粒间的滑移.至于这种颗粒间滑移是否属于摩擦滑移应视具体的微观机制而定.扩散蠕变主要类型包括:颗粒内扩散蠕变(纳-赫型扩散蠕变)(Nabarro,1948;Green,1970);颗粒边界扩散蠕变,具体分为固态形式的Coble蠕变(Coble,1963)和液相的压溶蠕变(Rutter,Elliott,1976;Rutter,1983).晶内塑性变形和扩散蠕变的本构关系均以高度非线性的形式依赖于温度.在恢复位错蠕变的本构关系中应变率以幂律关系依赖于应力(幂律蠕变),幂指数n一般为3—5,没有颗粒尺寸相依性.扩散蠕变的本构关系则是应变率与加载应力呈线性关系,与颗粒尺寸呈非线性关系(颗粒尺寸相依的牛顿流).值得注意的是颗粒边界滑移常伴随扩散蠕变发生,当颗粒边界滑移占主导作用时应力与应变率的关系是非线性的(应力指数一般为2),这导致在相同的物理和化学环境下会发生比扩散蠕变更快速的蠕变现象,甚至发生超塑性现象(Karato,2008).
岩石的变形机制图可用于粗略估计在特定环境下占主导作用的微观变形机制(Frost,Ashby,1982).变形机制图主要以温度(或均一温度)、加载应力量级、颗粒尺寸、加载应变率等变量构制(图1).值得注意的是,实际上岩石样品在加载的情况下各种微观机制都会发生,关键是要确定主导的机制.通常借助于岩石的组构和微观构造来判断已发生的微观机制.晶格的定向排列可由波速各向异性观测来评估(Ismail,Mainprice,1998).晶格的定向排列是否仅由位错蠕变造成,这可作为区分扩散蠕变与位错蠕变的依据.矿物颗粒中存在内部应变梯度也可作为发生过位错蠕变而不是扩散蠕变的依据.通常,位错蠕变主要发生在上地幔,扩散蠕变主要发生在应力较低的中下地壳,但中下地壳的断裂带边缘也可能会发生位错蠕变.直接将现有的蠕变机制推广到实际地球情况并不那么简单.首先是岩石圈内不同深度的真实形变机制不清楚,其次是真实的岩石圈形变与岩石力学的岩石形变存在时间和空间尺度上的巨大差异.岩石力学实验发生的速度明显快于一般情况下的构造现象的速度.例如,加载率差异(实验室的加载率范围是10-4—10-10s-1,岩石圈内一般则是10-13—10-17s-1),样品尺度差异(岩石样品一般是1—10mm,而我们所关注的实际问题的空间尺度则可能是10—1 000km).此外,深部岩石圈的温度结构不确定,岩石构成更为复杂(多种物质共存和单类物质以多相存在),以及现今的状态是地质历史上众多作用的综合结果等,这些都使得实验室结果的推广难度加大.
2 震后形变模拟理论基础
2.1 本构关系
在震后形变研究中被广泛应用的本构关系主要分为两大类:断层面上的余滑本构关系和分布式的韧性流本构关系(下地壳和岩石圈上地幔的黏弹性松弛).

图1 多晶黄铁矿(颗粒尺寸100μm)变形机制图(引自Barrie et al,2007)横坐标为温度,纵坐标为差应力(σ)的对数值,灰色等值线上的数字表示加载应变率的常数对数负值,其数字4表示10-4 s-1Fig.1 Deformation mechanism map for polycrystalline pyrite with grain size of 100μm(after Barrie et al,2007)The abscissa axis and ordinate axis indicate the temperature and constant logarithmic of the differential stress(σ),respectively.The numbers on the gray contours indicate negative constant logarithmic of the loading strain rates,for example,4is the loading at strain rate of 10-4 s-1
基于速率-状态摩擦准则(Ruina-Dieterich摩擦准则)的震后形变模型已成功解释很多地区地震周期内的地表形变时空演化特征(Hearn et al,2002;Johnson et al,2006;Johnson,Fukuda,2010;Barbot et al,2012).速率-状态摩擦准则可以用于模拟地震破裂成核和传播过程中断层面上的瞬态强度弱化和愈合过程.基于速率-状态摩擦准则下的震后动力学过程模拟成功解释了断裂带近场观测到的形变信号快速衰减特征,包括走滑型地震(Hearn et al,2002;Johnson et al,2006;Barbot et al,2009;Hearn et al,2009;Johnson et al,2009)和逆冲型地震(Perfettini,Avouac,2004;Hsu et al,2006;Perfettini,Avouac,2007).这种基于速率-状态摩擦准则的余滑主要发生在同震破裂的深部延伸部位或浅部的沉积层内.通常,速率弱化区域对应中浅部的同震破裂区域.在松散的沉积层中,断层面上主要表现为速率强化特征(Marone et al,1991);在沉积层之下的上中地壳断层面的摩擦性质主要表现为速率弱化特征;沿断层面继续向深部延伸,随着温度的增加速率弱化特征会转变为速率强化特征(Tse,Rice,1986).然而,深部的形变源也可能是分布式的韧性流,因此直接将岩石力学实验的结果推广到实际岩石圈下地壳和上地幔的有效性有待进一步研究.室温下的室内实验研究发现,当增加围压和降低滑动速率时,岩盐的力学性质会从摩擦滑动转变为韧性流(Shimamoto,1986).传统的基于速率-状态摩擦准则的余滑本构关系可解释地表形变观测数据,但与震后的地震活动性却不相关,而考虑速率强化的脆性蠕变本构关系却能同时模拟震后地表形变和余震活动的时间演变规律(Perfettini,Avouac,2004,2007).稳态的脆性蠕变本构关系为

式中,τ和¯σ分别为切应力和有效正应力;Vs为稳态滑动速率;t为时间;A1,A2,A3为经验常数.当滑动速率趋近于零时,Ruina-Dieterich摩擦准则(公式(2))与稳态的脆性蠕变本构关系等价.假设中地壳脆性蠕变区的库仑应力变化控制该区域断层周缘的小地震发生率,而库仑应力变化和地表形变都依赖于断层面余滑的时空变化,则地表形变和余震的发生率应遵从类似的时间演化规律.
至于分布式的韧性流动,早期的黏弹性松弛模型主要基于线性流变体来代表软流圈半空间(Nur,Mavko,1974;Rundle,1978;Thatcher,1983;Savage,1990)或者弹性层之下分层的黏弹性层(Pollitz,1992,1997).两类线性流变体(麦克斯韦尔体和标准线性固体)应用于黏弹性松弛模型中,其黏性部分本构关系可以简写为

式中,˙ε,σ和η分别表示应变率、差应力和黏性系数.更进一步的发展则是引入瞬态流变体,分别有宏观的经验性公式伯格斯体(Pollitz,2003b,2005)和微观机制的幂律流变律(Freed,Bürgmann,2004;Freed et al,2006a,2010,2012).伯格斯体的本构关系体现震后时间序列表现出的瞬态响应和稳态响应这两类运动,单纯使用麦克斯韦尔体则会损失对早期观测的拟合而仅拟合震后的后期观测.伯格斯体由麦克斯韦尔体和开尔文体串联组成,其中麦克斯韦尔体描述介质对瞬态加载的弹性反应和黏性变形中的稳态变化,开尔文体描述介质的瞬态黏性反应.伯格斯体的本构关系可以抽象表述为(Karato,2008)

式中,˙εss为稳态应变率;τ为瞬态变形的特征时间比,可由瞬态黏性系数除以瞬态剪切弹性模量来表示;β为瞬态和稳态应变率的比值.使用经验性的瞬态流变体所得到的瞬态和稳态黏性系数分别是瞬态相和稳态相期间的平均结果,故不能模拟与应力变化相关的时变流变学特征,而这种时变流变学特征却可由幂律流变体来近似模拟.幂律流变体在1992年Landers地震和1999年Hector Mine地震的震后形变中得到成功应用(Freed,Bürgmann,2004).最早期的幂律流变律是稳态蠕变律,其本构关系为

式中,A和K 为前因子(单位为MPa-n/s),σ为偏差应力,n为应力指数(对于扩散蠕变为1),Q为活化能,R为通用气体常数,T为绝对温度.早期的此类应用主要是为了检验幂律流变体在震后形变研究中的适用性,并没有细致考虑深部的物理和化学环境,所使用的流变模型只是某种意义上的简化(Freed,Bürgmann,2004;Freed et al,2006a).更严密的研究则表明,稳态的幂律流尽管成功拟合观测数据但无法真正解释震后观测,这是因为得到的物性参数无法与实际的构造环境兼容(Freed et al,2010).单纯引入稳态的幂律流无法同时模拟观测中的瞬态速率变化和稳态速率变化.瞬态与稳态流变规律组合则能在满足一定的构造环境条件下解释观测数据(Freed et al,2012).目前关于瞬态流变的微观机制还缺乏较统一的认识.若假定瞬态流变与稳态流变有相似的温度和应力相依性,则组合的幂律流变体的本构关系为
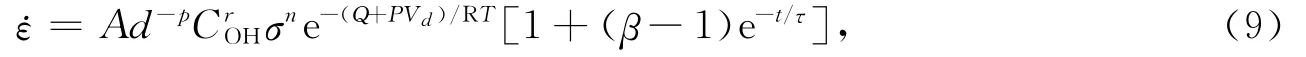
式中,τ为瞬态变形的特征时间比,β为瞬态和稳态应变率的比值,d为矿物颗粒尺寸,p为颗粒尺寸指数(对于位错蠕变为0),COH为水含量(原子水集合度,单位为H/106Si),r为水含量指数,P为压强,Vd为活化体积.其余参数意义与公式(8)一致.
2.2 数值模型
震后形变数值模型主要有解析模型、半解析模型和纯数值模型3类.解析模型主要模拟无限长的走滑断层其弹性层覆着在均质黏弹性半空间地球模型下的震后效应(Nur,Mavko,1974;Savage,Prescott,1978);半解析模型主要基于谱方法解决垂直向一维分层地球模型下的震后形变问题,地球模型具体分为平面分层模型(Rundle,1980;Wang et al,2006)和球状分层模型(Pollitz,1992,1997),在数值方法上则可分为波数域的积分(Wang et al,2006)和球谐函数若干项展开(Pollitz,1992,1997);纯数值模型主要有幂律流变体下的有限元方法(Hearn et al,2002;Freed,Bürgmann,2004).数值模拟计算结果表明,半解析模型和数值模型可以近似重现解析模型对应的震后形变时空演化特征.解析模型处理的情况简单,计算快速;相对于解析模型,半解析模型可以模拟有限长断层与多层介质近似的地球模型相关的震后形变,然而,半解析模型的黏弹性介质仅限于线性流变本构关系.而纯数值模型则可以克服这一缺陷,但纯数值模型较其它两类模型的计算更耗时.
对于准静态问题的解析模型和半解析模型,黏弹性介质的引入借助于对应原理,即在一定的加载条件下静态问题与黏弹性问题的弹性解在拉普拉斯域的转换解的形式上是等价的.只要得到相关问题的弹性解,将其中的弹性模量替换为对应的拉氏域弹性模量,并对转换后拉氏域的解进行拉普拉斯逆变换就可以得到所对应的黏弹性问题在时空域的解.这类模型一般采用线性流变体(如麦克斯韦尔体、标准线性固体、伯格斯体等).当拉氏域的问题找不到解析的拉普拉斯逆变换时,只能采用数值的方法来近似求解(半解析模型).
下面以弹性层内无限长走滑断层覆着在均质黏弹性半空间地球模型之上的震后黏弹性松弛解为例介绍解析模型.在均质弹性半空间模型下,无限长走滑断层震间深部蠕滑运动对应的地表位移场可由螺旋位错对应的形变场来表示(Savage,Burford,1973).然而我们需要考虑用分层的地球模型来模拟实际地球介质流变学的分层特征.基于螺旋位错的解并采用镜像位错的思路,Rybicki(1971)获得了弹性分层模型下无限长走滑断层位错对应的位移场.假定剪切模量为μ1、厚度为H的弹性层上覆于剪切模量为μ2的弹性半空间,在深度为D(D<H)之下存在一位错量为ΔU的无限长走滑断层,则相应的地表位移场可以表述为

式中,x为观测点距断层的垂直距离.假定黏弹性半空间(对应于深度在H以下的弹性半空间)由麦克斯韦尔体构成,黏性系数为η,弹性模量为μ,则本构关系为

式中,σ为差应力,ε˙和˙σ分别为应变和差应力对时间的导数.其对应的拉氏域的本构关系为

其中

如果将公式(10)中的μ2用公式(13)替换,并同时把ΔU按照下式替换为ΔU(s),则

我们便得到了拉氏域的黏弹性解,再进行拉普拉斯逆变换便得到在上述分层模型下无限长走滑断层对应的震后时变位移场的解析解(Nur,Mavko,1974).震后时变位移场可表示为

此外,对应的弹性层内无限长倾滑断层覆着在均质黏弹性半空间地球模型之上的震后时变位移场可由刃位错的弹性解得到.
下面以Wang等(2006)研制的PSGRN/PSCMP震后形变模拟软件包的核心理论为例介绍半解析模型.PSGRN/PSCMP模拟软件包涵盖主要的线性黏弹性介质有麦克斯韦尔体、标准线性固体和伯格斯体;震源包括走滑型、逆冲型、爆炸型和补偿线性向量偶极型4种.其中,PSGRN模拟软件包计算格林函数,PSCMP模拟软件包计算具体同震位错下对应的时变形变场.PSGRN模拟软件包采用平面分层地球模型并满足基于Adams-Williamson条件下的密度梯度模型计算,考虑自重和流体静压力下地球地表和近地表的震后时变形变场和时变重力场及大地水准面的变化.柱坐标系下模型的本构方程为
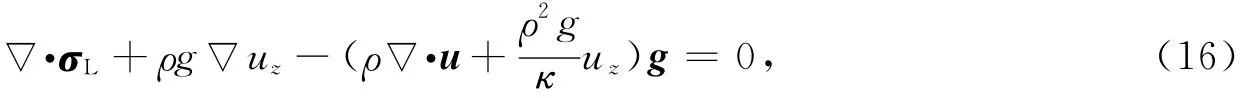
式中,σL为拉格朗日增量应力张量;u和g分别为位移矢量和重力加速度矢量;uz为位移的垂向分量;ρ为密度;κ为体积模量;g为重力加速度(1g=9.8m/s2);z轴方向由地表垂直指向地球深部.Adams-Williamson条件使得密度的梯度变化满足初始流体静压力平衡条件,并可以表述为

使用Hankel变换,黏弹性松弛问题的偏微分方程组描述转换为波数域内的常微分方程组.在波数域,常微分方程组的解为

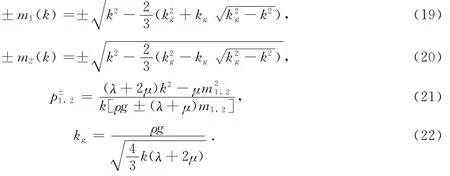
其中使用对应原理将解中的弹性模量参数替换为对应的拉氏域弹性模量,再使用快速傅里叶变换算法进行逆变换得到规则网格点的时变格林函数.一旦格林函数计算完成并指定具体的地震源,PSCMP模拟软件包可插值计算待考察点的时变震后形变.
类似的半解析模型软件包还有平面分层模型v3fasat(Fukahata,Matsu’ura,2006)和VISCO1D软件包(Pollitz,1997).前者类似于PSGRN/PSCMP模拟软件包,但只能计算规则网格点上的时变形变场;VISCO1D软件包则考虑球状分层的地球模型,并将解用简正模型展开,故实际使用时存在最大球谐函数阶数的截止问题,这会对长时间尺度的形变场计算造成一定的偏差.以上的半解析模型均采用横向均匀介质,Pollitz(2003a)在类似理论框架下发展了考虑层内介质横向不均匀性的半解析模型,但实际应用的案例很少(Pollitz et al,2008).
纯解析模型的最主要代表是以有限元模拟方法为基础并考虑幂律流变体的震后形变模拟(Hearn et al,2002;Freed,Bürgmann,2004).对于这类非线性本构关系下的黏弹性松弛模拟问题,首先要指定形变系统震前初始物理状态以获得背景场,然后要考虑系统受同震破裂加载激发系列震后效应,再将不同流变模型对应的模拟形变与观测形变进行对比,以获得合理的区域岩石圈流变结构.
3 美国南加州震后形变研究
本文主要以美国南加州地区的震后形变研究为例,简述震后形变的研究进展.美国南加州1992年Landers MW7.3地震和1999年Hector Mine MW7.1地震均为走滑型地震,发生在区域地质构造背景相对简单的南加州Mojave沙漠地区.丰富的震后GPS和InSAR观测在大陆地震震后形变研究中实属罕见,震后形变研究的许多开创性成果均来自于该地区的研究案例.已有系列学术论文研究南加州Mojave沙漠的两次大地震(1992年Landers MW7.3地震和1999年Hector Mine MW7.1地震)的震后形变(Shen et al,1994;Massonnet et al,1996;Savage,Svarc,1997;Deng et al,1998;Peltzer et al,1998;Pollitz et al,2000,2001;Pollitz,2003b;Jacobs et al,2002;Masterlark,Wang,2002;Owen et al,2002;Freed,Bürgmann,2004;Freed et al,2007,2010,2012;Pollitz,Thatcher,2010).另一类震后形变研究热点集中在大洋俯冲带大地震的震后形变上(Khazaradze et al,2002;Hsu et al,2006;Kreemer et al,2006;Paul et al,2007;Ozawa et al,2011).俯冲带的地质构造背景比区域性单剪作用下的地质构造更复杂.在海洋与大陆岩石圈汇聚处,海洋地壳向大陆岩石圈深部下插并继续俯冲至地幔,与这一过程相伴的变形和变质作用造成俯冲板片与大陆岩石圈接触面上岩石的流变学性质由浅至深发生显著的变化.洋壳俯冲还使得陆侧深部形成地幔楔体.俯冲带大地震主要发生在俯冲板片浅部的震间锁定部位,但俯冲板片面上的震后余滑和黏弹性松弛可造成比走滑地震更复杂的震后形变场时空演化特征(Wang et al,2012).
目前,震后形变的理论和实例研究提出4类机制解释震后形变,这些机制分别是:余滑、断裂带坍塌、孔隙弹性回弹和黏弹性松弛.地震是由于脆性层内完整岩石的破裂或沿着先存断层的突然失稳滑动造成的.失稳伴随着震源附近的应力降和对周边断层、岩石和脆性层之下的黏弹性层进行加载的过程.对断层面震源区上下部位以及邻近部位的加载可能会造成限于断裂面附近的余滑(Tse,Rice,1986;Marone et al,1991;Marone,1998).断裂带坍塌表现在近场垂直于断裂带走向的地壳缩短,因为震后断裂带内扩容破裂的闭合和同震过压加载造成的流体滞后流动会造成断裂带内物质的体积变化(Massonnet et al,1996;Feigl,Thatcher,2006).孔隙弹性回弹效应是因同震破裂产生的应力变化造成上地壳断层附近的多孔介质内孔隙压变化,从而驱使流体流动进而造成震后短时间内的地表近场形变(Peltzer et al,1998).黏弹性松弛起因于黏弹性层无法承受同震破裂造成的瞬态加载并随时间释放应力继而对浅部的上地壳进行加载,最终造成长期的大范围内地表可观测形变(Nur,Mavko,1974).余滑造成断层近场在震后数年之内出现快速的震后形变,而断裂带坍塌造成的地壳缩短则主要局限在断裂带几百米至几千米范围之内,孔隙弹性回弹效应也主要局限在断裂带近场,黏弹性松弛效应则在断裂带远场数十年时间尺度内造成可观测到的震后形变.实际的震后形变观测一般难以提供理想的时空覆盖,加之实际岩石圈流变学结构和震后形变源的复杂性,使得地表观测难以有效约束震后形变源.若单从震后形变的数值模型角度分析,不同机制的模型可在断层近中场产生具有相似时空演化特征的地表形变场,这使得实际的震后形变研究变得复杂.对于具有均匀滑动的无限长垂直走滑断层,满足一定分布的余滑模型对应的地表形变与岩石圈-软流圈模型黏弹性松弛造成的地表形变是一致的(Savage,1990),故在此背景下分辨余滑与黏弹性松弛两种形变源比较困难.但模拟试验却发现对于有限长断层,如果在一些比较关键的观测点(平行于断层走向延伸方向和垂直于断层走向)有观测数据,这种形变源模糊问题则不存在(Hearn,2003).
震后形变的形变源模糊问题可从南加州的1992年Landers MW7.3地震和1999年Hector Mine MW7.1地震的众多研究中体现.对于Landers地震震后形变解释的机制包括:① 余滑(Shen et al,1994;Savage,Svarc,1997);② 断层坍塌(Massonnet et al,1996);③ 孔隙弹性回弹和余滑(Peltzer et al,1998;Fialko,2004);④ 黏弹性松弛.下地壳松弛占主导(Deng et al,1998)和岩石圈上地幔松弛占主导(Pollitz et al,2000).对于Hector Mine地震,震后形变源的模糊问题仍然存在,仍没有统一的认识,目前主要有三大观点:① 岩石圈上地幔松弛占主导的黏弹性松弛(Pollitz et al,2001;Pollitz,2003b;Freed,Bürgmann,2004;Freed et al,2007;Pollitz,Thatcher,2010);② 余滑.断层深部余滑(Owen et al,2002;Perfettini,Avouac,2007)和浅部余滑(Jacobs et al,2002);③孔隙弹性回弹和下地壳的黏弹性松弛(Masterlark,Wang,2002).下面我们简要介绍上述地区典型的震后形变研究案例.
基于位错理论,Shen等(1994)主要以Landers地震震后6个月近场的流动GPS站间基线相对位移时间序列为约束,反演得到了Landers地震同震破裂断层和周边断层以及各自深部延伸面上的余滑分布.震后余滑的矩释放主要分布在10km深度以下断层面,在10 km深度以上与余滑相对应累积的地震矩释放与同时期的余震地震矩释放相当.通过指数松弛函数拟合基线位移时间序列获得衰减时间常数为34d(70%置信区间为15—150d),以距震中以南约80km的PIN1站为基准,累积位移在近场台站可达到55mm,并在中远场衰减至数毫米.
Massonnet等(1996)分析两幅覆盖Landers地震同震破裂区域的欧空局ERS-1雷达卫星影像对(震后5—1 008d和震后40—355d),并组合该两幅干涉图像以分析震后形变的空间特征.组合干涉图像清晰显示,以34.5°N为界沿着断层走向存在着显著的形变特征.其中北部跨断层两侧的视线沿距离变化反向,而南部则沿着断层数千米范围内有统一显著的局部变形.沿着同震破裂带内6—11km深度范围内发生约90cm的余滑可解释北部形变特征,而南部形变特征可由垂直于断层走向的闭合运动(30cm)和余滑(量级约为北段断裂余滑的70%)来解释.其中垂直于断层走向的闭合运动(断裂带坍塌)可能是同震破裂扩容的震后闭合和富含水的断裂带内震后水的流动造成的.
Savage和Svarc(1997)使用主成分分析法分析Landers地震震后3.42aEmerson跨断层近场流动GPS观测数据,发现GPS台站位置的震后时间演化特征是短期衰减(指数特征衰减时间为(84±23)d)和长期衰减(特征衰减时间至少为5a)的叠加.余滑模型(同震破裂断层面延伸在10—30km深度范围内产生约0.6m的累积余滑)可在一定程度解释震后的地表累积形变,但没有任何余滑模型可拟合断层倾向方向的形变分量,实际观测受到断层三维几何形态的影响.
Deng等(1998)试图采用三维黏弹性松弛模型来解释Emerson跨断层近场流动GPS观测数据和Massonnet等(1996)使用的InSAR数据(Deng et al,1998).模拟结果发现,下地壳黏弹性松弛模型(下地壳黏性系数为1018Pa·s,岩石圈上地幔黏性系数为1020Pa·s)可以同时解释沿断层走向法向和平行方向的震后形变,而余滑模型仅能拟合沿断层走向方向的形变,黏弹性松弛模型还可以很好地解释跨Emerson断层两侧的InSAR视线向位移变化特征.
Peltzer等(1998)发现,深部余滑模型和孔隙弹性回弹组合模型可以解释覆盖Landers地震震中近中场的ERS-1卫星干涉图的形变信息,其时间覆盖为1992-09-27—1996-01-23.孔隙弹性回弹因微观上震后地壳浅部孔隙之间的流体流动导致孔隙压逐渐变化,并在宏观上造成地壳岩石体积变化所产生.地震发生时孔隙处于未排水状态,而震后孔隙处于排水状态.孔隙弹性回弹在力学效果上可用同震和震后的岩石泊松比变化造成的地表形变来近似模拟(泊松比由同震时的0.31衰减至震后的0.27).余滑模型仅可解释水平向的近场震后形变场,其正演的垂向位移场与实际观测的空间分布特征相反,故余滑模型正演的三维形变场转换至InSAR视线向后与InSAR观测到的视线向位移场特征相反.余滑和孔隙弹性回弹组合模型可同时解释水平向和垂向的观测.
Pollitz等(2000)以1992年Landers地震震后3个月—3年的GPS(覆盖近中远场)和InSAR数据为约束,发现余滑和孔隙弹性回弹模型或者二者的组合模型均无法同时解释观测数据,而以岩石圈上地幔松弛占主导的黏弹性松弛模型可成功解释数据的总体特征.岩石圈上地幔(深度30—50km)的黏性系数为8.0×1018Pa·s(为下地壳黏性系数的0.5倍),长期的剪切强度为12GPa,50km上、下两层上地幔的黏性系数比为3.该模拟结果支持Mojave沙漠地区存在具有高度韧性流变的岩石圈上地幔,区域的形变特征和断层分布受这一流变学结构控制.Pollitz等(2001)发现,上地幔松弛占主导的黏弹性松弛模型仍可解释Hector Mine地震震后9个月内的GPS数据和InSAR数据,上地幔黏性系数约为3.0×1017—8.0×1017Pa·s(下地壳与上地幔黏性系数比为27),并据此提出走滑断层地震震后上地幔的快速韧性流动是地震周期内岩石圈变形的一个普遍特征,上地壳变形与上地幔变形之间通过下地壳的作用而耦合.
Pollitz(2003b)根据1999年Hector Mine地震震后2.5a近中场连续GPS观测(南加州GPS集成网)发现普遍存在的瞬态相和稳态相的时间演化特征这一事实,提出深部的震后形变源也应具有瞬态和稳态两相,并发现伯格斯体这种考虑瞬态变形的流变体可解释震后的连续和流动观测,其中合理的黏弹性流变学结构为伯格斯体的上地幔(瞬态黏性系数为1.6×1017Pa·s,稳态黏性系数为4.6×1018Pa·s,瞬态和稳态剪切强度相等)和麦克斯韦尔体的下地壳(黏性系数为3.2×1019Pa·s).
以1992年Landers地震震后6a和1999年Hector Mine地震震后3a的GPS观测(南加州GPS集成网)为约束,Freed和Bürgmann(2004)以幂律流变体的黏弹性松弛模型成功地解释了这两次地震的震后地表形变时空演化特征.系统分析了下地壳和上地幔的矿物组合、地温剖面和下地壳与上地幔黏弹性松弛形变的贡献比,模拟结果表明震后黏弹性松弛主要发生在高温(50km深度处约1 300℃)由湿橄榄石为主构成的上地幔内.下地壳黏弹性松弛占主导的模型所预测的垂直向形变特征与观测值所反映的空间特征反相关,而传统的牛顿流线性黏弹性松弛难以同时拟合震后GPS观测早期的瞬态相和后期的稳态相.
基于Hector Mine地震震后7a远场GPS观测在距震中区200多千米地表仍有明显的震后形变信号.Freed等(2007)提出震后形变源为40km深度以下上地幔存在大范围的黏弹性松弛,而不是局限在断层下方狭窄的剪切带内.下地壳黏弹性松弛模型所预测的垂向运动空间分布与观测值及上地幔黏弹性松弛模型预测值的特征相反.孔隙弹性回弹模型对应的垂向运动趋势特征虽然与观测值相同但主要局限在断层附近,故孔隙弹性回弹模型无法解释大范围的垂向运动特征,而仅当深度为400km处仍发生震后蠕滑的余滑模型才可拟合远场的水平向观测数据,但这种深部余滑的存在性在现实条件中几乎不可能.
Freed等(2010)仍以Hector Mine地震震后远场观测为约束,系统检验稳态的幂律流在震后形变研究中的适用性,结果证实没有任何湿橄榄石的稳态的扩散蠕变和稳态的位错蠕变本构关系可在符合相应深部物理环境的条件下解释观测数据.稳态的扩散蠕变和位错蠕变黏弹性松弛模型均认为黏弹性松弛主要发生在45—70km深度.考虑到深部的物理环境(温度,矿物颗粒尺寸,原子水含量,背景应变率),基于稳态扩散蠕变和位错蠕变的黏弹性松弛模型尽管都可以拟合震后7a的累积形变,但都不能较好地拟合震后GPS台站位置时间序列.稳态的幂律流变律黏弹性松弛模型都不能拟合震后早期GPS台站的快速运动,基于稳态位错蠕变的模型当且仅当在与现实构造物理环境极其不兼容的条件下(50km深度、1 700℃温度和10-8a-1背景应变率)才可重现GPS观测.假设瞬态和稳态蠕变具有相似的温度和应力相依性,Freed等(2012)发现组合的瞬态和稳态蠕变本构关系可以成功解释Hector Mine地震震后GPS观测.模拟证实震后的黏弹性松弛主要以50km以下深度的位错蠕变为主,瞬态蠕变特征衰减时间约为1a,稳态和瞬态蠕变黏性系数比值约为10.震后GPS观测支持高温上地幔(深度50km、温度为1 200—1 300℃,稳态黏性系数约1019Pa·s)的背景应变率约为1×10-7—2×10-7a-1.在上地幔的物理环境下,参照实验的矿物颗粒尺寸演化经验关系估计矿物颗粒尺寸约为10—20mm.这一事实排除扩散蠕变发生的可能性,因为扩散蠕变观测数据的矿物颗粒尺寸为3.5mm.
上述震后形变模型均能解释所使用观测数据的主体时空分布特征,但观测数据在时间覆盖(震后若干天至数月数年)和空间覆盖(近场和/或远场)、观测策略(连续观测或流动观测)、剔除震前背景场的方法、多源单类数据(例如USGS和SCIGN/SCEC GPS)与多类数据(GPS和InSAR)的统一方案上有差异.最理想的观测数据应提供一个覆盖完整地震周期的高质量近中远场三维形变约束.Landers地震和Hector Mine地震属于走滑型地震,相对于水平向震后形变,垂向的震后形变并不是特别显著,现有研究表明垂向形变有助于分辨各种形变源.但GPS垂向观测误差太大,难以提供信噪比较高的垂向形变时间序列,InSAR虽对垂向形变敏感,可已有研究使用的InSAR数据在中远场信噪比较低.此外,GPS观测缺乏足够的震后时间覆盖,尤其是Landers地震震后形变观测多为流动观测,两次地震的震后观测时间均不够长,这些因素使得研究震后的瞬态和稳态形变源变得困难.震后形变研究最感兴趣的信号是真正与震后形变相关的信号,而GPS观测得到的位置时间序列中包含震间形变的信号,如何剔除震间形变的干扰又是个关键问题.对于Mojave沙漠地区Landers地震震前GPS观测稀少且受到震后信号干扰这一事实,目前仍难以获得一个十分可靠的区域震间速度场模型.Landers地震和Hector Mine地震震后形变研究往往采用现有区域震间形变或者速度场模型,或者采用不同时间段震后速度差分来剔除震后观测中的震间形变干扰.但是现有的速度场是通过数学函数拟合GPS时间序列获得的,难以有效分辨震间形变与震后形变.而现有区域震间形变模型却往往以这些速度场模型为约束,或者以稀少的震前历史三角或者三边观测为约束,这些都使得剔除区域性的震后GPS观测中的震间形变信号难度加大.震后不同时间段差分方法理应可完全剔除震间形变信号,但这类方法以牺牲真实观测数据的约束力为代价.为获得整个GPS观测网统一的时间段形变信息往往需要使用拟合后的时间序列,对于流动GPS观测,拟合后的时间序列会失去某些特定时间段的形变细节(如震后早期和后期无观测数据时期).
至于震后形变建模分析,目前尚没有一个真正意义上的综合性模型.幂律流变律模型仍然没有考虑多相物质和部分熔融物质的本构关系,没有一个模型同时考虑具有力学背景的余滑模型和幂律流变律黏弹性松弛模型.根据现有的震后形变数值模型,余滑和黏弹性松弛是必然存在的,二者只是在近远场和震后不同时期对地表形变信号的贡献存在差异.单独通过震后形变观测数据约束获得的余滑和黏弹性松弛仍不会轻易被接受为合理的模型.严格的建模分析应该综合地质和地球物理信息所能提供的区域岩石圈结构和断裂带结构信息.区域的地表断裂分布与历史地质构造作用有关,密集断层分布(分布式的连续变形)和零星断层分布(局部化的非连续变形)与岩石圈流变学结构密切相关.地球物理观测也为岩石圈流变学结构和其它物理性质提供宝贵约束.地震各向异性研究(主要是剪切波分裂)可为走滑断层下方岩石圈地幔的连贯形变和微观变形机制提供宝贵约束,尽管其空间分辨率一般为数十千米.直接的地表热流、基于面波的岩石圈品质因子Q和剪切波波数研究可从一定程度上揭示岩石圈深部的地温剖面.尽管沿走滑断裂地表难以发现深部的地幔岩体出露,但在整个大区域背景下发现的火山附近的岩体样本则可能为深部的形变介质提供一定的线索.针对走滑型断层,目前争议的焦点之一就是其深部延伸形态究竟是局部化的延伸还是分布式的弥散分布,而剪切波分裂难以有足够的分辨力区分这种断裂带细节结构.这些因素说明我们仍然不能肯定断层深部在下地壳和上地幔部分究竟是发生局部化变形还是分布式变形或者是从浅部至深部的二者过渡.至于孔隙弹性回弹则依赖于上地壳孔隙流和渗透率等研究作为参考,同时依赖于震后时空变化的深部应力场研究,而目前的孔隙弹性回弹模型仅是为计算方便而做的某种近似假设(认为整个上地壳都发生孔隙流).
4 岩石圈流变学结构
大陆岩石圈强度的深部变化特征一直是争议很大的问题.Goetze和Evans(1979)首次提出具有地学意义的屈服强度剖面模型.这种模型认为岩石圈强度由脆性强度和韧性强度决定,其中脆性强度由随深度增加并依赖围压的摩擦强度控制,韧性强度由温度相依的蠕变过程控制.Brace和Kohlstedt(1980)根据岩石圈构成成分的分层性及其对应的流变学特征提出浅部脆性摩擦和深部不同的韧性流组成的分层强度剖面模型.该分层模型的黏弹性层由软的下地壳和韧性屈服强度更大的上地幔组成.然而,由于不同构造背景下深部岩石的镁铁矿成分和水(或者结构水)含量差异大,而镁铁矿含量和微量的水对韧性强度影响显著,因此,Kohlstedt等(1995)提出了更复杂的分层强度剖面.
对于整个岩石圈,目前主要存在两种主流的概念性强度剖面模型,即“三明治模型”和“焦糖布丁模型”.这两种模型可以由不同的地温线与含水量不同的长石英质下地壳和橄榄石质上地幔组合而成(Brace,Kohlstedt,1980;Chen,Molnar,1983;Jackson,2002;Bürgmann,Dresen,2008).此外,对于断裂型板块边界带,还存在“香蕉皮模型”,即上地壳的摩擦强度和下地壳的韧性强度因不同的弱化机制作用而较板内岩石圈上下地壳显著降低.
根据西藏地区的震源分布局限在上地壳和上地幔这一现象,Chen和Molnar(1983)提出了更高强度的岩石圈地幔和软的无震下地壳这一观点.在地质时间尺度下,下地壳流和上地壳流与上地幔运动之间的解耦,成功地解释了地表形变演化,该结果也同时支持“三明治模型”(Royden et al,1997).然而,上地幔地震的缺少和有效弹性厚度小于地震孕震厚度却支持“焦糖布丁模型”,即岩石圈的强度主要取决于孕震层而岩石圈地幔相对较软.Afonso和Ranalli(2004)系统分析了系列因素(层厚度、组成、温度等)对岩石圈强度的影响,认为“三明治模型”主要与低地表热流值、薄的地壳和酸性的或湿的镁铁质下地壳成分相关;而“焦糖布丁模型”则主要与高的地表热流值和干的镁铁质下地壳组成相关;Burov和Watts(2006)则通过热力学模拟支持传统的“三明治模型”,然而并不能排除“焦糖布丁模型”的可能性.Thatcher和Pollitz(2008)则认为并不存在一个统一的岩石圈强度模型,岩石圈的强度模型应该考虑具体问题所依赖的时间尺度和构造背景;认为在长于地震周期的地质时间尺度下,岩石圈上地幔比地壳柔弱,下地壳在地震周期和冰后均衡调整时间尺度上更强,在岩石圈均衡作用和稳态的形变过程中则更柔软;提出在快速拉张或者碰撞的构造环境下高温热异常区域往往存在柔软的下地壳.
对于区域性的岩石圈流变学结构研究,我们以南加州的Landers地震和Hector Mine地震震后形变研究为例进行介绍.绝大部分关于Landers和Hector Mine地震的震后形变研究认为相比下地壳的黏弹性松弛而言,岩石圈上地幔的黏弹性松弛对地表观测到的震后形变贡献更大(Pollitz et al,2000,2001;Pollitz,2003b;Freed,Bürgmann,2004;Freed et al,2007).这些研究支持Mojave地区的岩石圈流变学结构为“焦糖布丁模型”.该模型在其它构造环境下也得到证实(Gourmelen,Amelung,2005;Pollitz,2005;Freed et al,2006a,b).“三明治模型”被拒绝的原因有:① 对应的垂向位移与观测到的垂向位移趋势反相关;② 无法模拟远场的观测数据.仅有一种震后形变模型支持这个区域的岩石圈流变学结构为“三明治模型”(Deng et al,1998),但这种解释的有效性值得进一步考虑,因为其使用的Landers地震破裂南部地区的InSAR数据方法不明确.“三明治模型”还成功用于解释贝加尔-蒙古地区现今的GPS观测(Vergnolle et al,2003)以及柴达木盆地地区2001年可可西里地震震后形变(Ryder et al,2011).
震后形变资料约束下的南加州Mojave沙漠地区的流变学结构为何与传统的“三明治模型”相矛盾?仅从最初得出“三明治模型”的岩石力学依据来看,我们可以怀疑其下地壳和上地幔代表性岩石的可靠性.因为下地壳一般是由长石和辉石组成,而在最初得出“三明治模型”的研究则认为是由石英构成(Rudnick,Fountain,1995).在下地壳环境中,长石和辉石较石英有更强的流变学强度,这种观点支持目前的震后形变研究结果.但最新的研究却认为该区域的地壳主要由石英构成(Lowry,Pérez-Gussinyé,2011),所以支持“三明治模型”.目前,支持“焦糖布丁模型”的研究均认为岩石圈地幔的稳态黏性系数约为1018Pa·s,该量级低于其它地区更长时间尺度现象下的稳态黏性系数,如冰后回弹研究认为相应的黏性系数大于1020Pa·s.这类研究均认为更强的下地壳和软的岩石圈地幔这一现象归因于更高的地幔温度(莫霍面温度>800℃),而这一高温与区域的拉张地质作用有关.但是这种解释并没有严格的定量分析,毕竟因拉张造成的岩石圈减薄、相伴的岩石圈温度增加对岩石圈流变学结构演化产生显著效果的时间尺度仍不得而知.此外,各类研究仍不能明确地阐述不同时间尺度下短期和长期流变学结构的演化规律.仅从这些角度分析,以目前的理论分析和观测约束,要获得对区域岩石学流变结构统一的认识仍不具备充分条件.
5 结论
目前,震后形变研究的常规思路主要如下:以形变大地测量观测为约束,基于震后形变的物理模型(黏弹性松弛和/或动力学的速率-状态摩擦本构关系背景下的余滑或运动学的余滑)获得区域的岩石圈流变学结构和/或断裂带的力学性质.然而,大地测量观测所捕捉到的形变时空演化信息(暂且忽略原始的观测数据处理)却与岩石圈的深部物理状态(区域的岩石圈流变学结构和断裂带的力学性质)及快速剧烈的地震加载和长期慢速的区域地质构造作用直接相关.尽管因地震同震破裂对周围介质的加载激发出一系列震后效应,震后一定时期内震间形变场的信号会被震后形变信号几乎完全“淹没”,但绝不能因此忽略区域的地质构造演化史,因为现今区域的岩石圈深部物理状态(依赖于观测时间尺度)也是长期地质作用的结果.因此,我们不仅要重视现今的观测及其对应的模拟建模计算,还要尊重过去的地质构造演化史.由于无法真正直接接触岩石圈深部介质,所以研究其物理状态要借助于间接观测和理论推估.例如,地震学和重力学的研究方法能够提供一些信息(深部结构和有效弹性厚度)用以约束岩石圈的流变学结构,而岩石力学实验能够在室内实验室条件下直接认识地球深部岩石的力学行为及其对应的本构关系.尽管将实验室条件下的结论推广到真实岩石圈环境下存在尺度标定问题(时间尺度和空间尺度),但岩石力学实验至少为深部岩石的力学行为提供了定性分析和定量描述.因此,震后形变研究须结合岩石力学实验研究结果进行直接的物理模型建模或者间接的理论推估.
岩石圈强度研究是一个学科综合性很强的研究方向,是目前地学研究中的热点和难点之一.然而,我们对此的认知仍然处于初级阶段,一方面缺乏足够好的观测数据提供约束,一方面理论认识水平仍不够深刻.目前,我们唯一可以确定的是岩石圈强度的深部变化特征具有成层性.20世纪70年代末以来,不论是将岩石力学得到的流变学准则推广到地质时间尺度下的岩石圈强度研究,还是基于解析模型和数值模型解释不同构造背景下岩石圈形变的总体特征研究,都支持这一观点.但是,我们仍不能获得对层间相对强度统一的认识.
Afonso J C,Ranalli G.2004.Crustal and mantle strengths in continental lithosphere:Is the jelly sandwich model obsolete?[J].Tectonophysics,394(3/4):221--232.
Barbot S,Fialko Y,Bock Y.2009.Postseismic deformation due to the MW6.0 2004Parkfield earthquake:Stress-driven creep on a fault with spatially variable rate-and-state friction parameters[J].J Geophys Res,114(B7):B07405.doi:10.1029/2008JB005748.
Barbot S,Lapusta N,Avouac J P.2012.Under the hood of the earthquake machine:Toward predictive modeling of the seismic cycle[J].Science,336(6082):707--710.
Barrie C D,Boyle A P,Prior D J.2007.An analysis of the microstructures developed in experimentally deformed polycrystalline pyrite and minor sulphide phases using electron backscatter diffraction[J].J Struct Geol,29(9):1494--1511.
Bodine J H,Steckler M S,Watts A B.1981.Observations of flexure and the rheology of the oceanic lithosphere[J].J Geophys Res,86(B5):3695--3707.
Brace W F,Byerlee J D.1966.Stick-slip as a mechanism for earthquakes[J].Science,153(3739):990--992.
Brace W F,Kohlstedt D L.1980.Limits on lithospheric stress imposed by laboratory experiments[J].J Geophys Res,85(B11):6248--6252.
Buck W R.1991.Modes of continental lithospheric extension[J].J Geophys Res,96(B12):20161--20178.
Bürgmann R,Dresen G.2008.Rheology of the lower crust and upper mantle:Evidence from rock mechanics,geodesy,and field observations[J].Ann Rev Earth Planet Soc,36(1):531--567.
Burov E B,Watts A B.2006.The long-term strength of continental lithosphere:“jelly sandwich”or“crème brûlée”?[J].GSA Today,16(1):4--10.
Byerlee J.1978.Friction of rocks[J].Pure Appl Geophys,116(4):615--626.
Chen W P,Molnar P.1983.Focal depths of intracontinental and intraplate earthquakes and their implications for the thermal and mechanical properties of the lithosphere[J].J Geophys Res,88(B5):4183--4214.
Coble R L.1963.A model for boundary diffusion controlled creep in polycrystalline materials[J].J Appl Phys,34(6):1679--1682.
Deng J,Gurnis M,Kanamori H,Hauksson E.1998.Viscoelastic flow in the lower crust after the 1992Landers,California,earthquake[J].Science,282(5394):1689--1692.
Dieterich J.1994.A constitutive law for rate of earthquake production and its application to earthquake clustering[J].J Geophys Res,99(B2):2601--2618.
Dieterich J H.1972.Time-dependent friction in rocks[J].J Geophys Res,77(20):3690--3697.
Dieterich J H.1978.Time-dependent friction and the mechanics of stick-slip[J].Pure Appl Geophys,116(4):790--806.
Dieterich J H.1979.Modeling of rock friction:1.Experimental results and constitutive equations[J].J Geophys Res,84(B5):2161--2168.
Feigl K L,Thatcher W.2006.Geodetic observations of post-seismic transients in the context of the earthquake deformation cycle[J].C R Geosci,338(14/15):1012--1028.
Fialko Y.2004.Evidence of fluid-filled upper crust from observations of postseismic deformation due to the 1992 MW7.3 Landers earthquake[J].J Geophys Res,109(B8):B08401.
Flemings P B,Jordan T E.1990.Stratigraphic modeling of foreland basins:Interpreting thrust deformation and lithosphere rheology[J].Geology,18(5):430--434.
Freed A M,Bürgmann R.2004.Evidence of power-law flow in the Mojave desert mantle[J].Nature,430(6999):548--551.
Freed A M,Bürgmann R,Calais E,Freymueller J.2006a.Stress-dependent power-law flow in the upper mantle following the 2002Denali,Alaska,earthquake[J].Earth Planet Sci Lett,252(3/4):481--489.
Freed A M,Bürgmann R,Calais E,Freymueller J,Hreinsdóttir S.2006b.Implications of deformation following the 2002Denali,Alaska,earthquake for postseismic relaxation processes and lithospheric rheology[J].J Geophys Res,111(B1):B01401.doi:10.1029/2005JB003894.
Freed A M,Bürgmann R,Herring T.2007.Far-reaching transient motions after Mojave earthquakes require broad mantle flow beneath a strong crust[J].Geophys Res Lett,34(19):L19302.doi:10.1029/2007GL030959.
Freed A M,Herring T,Bürgmann R.2010.Steady-state laboratory flow laws alone fail to explain postseismic observations[J].Earth Planet Sci Lett,300(1/2):1--10.
Freed A M,Hirth G,Behn M D.2012.Using short-term postseismic displacements to infer the ambient deformation conditions of the upper mantle[J].J Geophys Res,117(B1):B01409.doi:10.1029/2011JB008562.
Frost H J,Ashby M F.1982.Deformation Mechanism Maps[M].Oxford:Pergamon Press:3--5.
Fukahata Y,Matsu’ura M.2006.Quasi-static internal deformation due to a dislocation source in a multilayered elastic/viscoelastic half-space and an equivalence theorem[J].Geophys J Int,166(1):418--434.
Goetze C,Evans B.1979.Stress and temperature in the bending lithosphere as constrained by experimental rock mechanics[J].Geophys J R astr Soc,59(3):463--478.
Gourmelen N,Amelung F.2005.Postseismic mantle relaxation in the central Nevada seismic belt[J].Science,310(5753):1473--1476.
Green H W.1970.Diffusional flow in polycrystalline materials[J].J Appl Phys,41(9):3899--3902.
Hearn E H,Bürgmann R,Reilinger R E.2002.Dynamics of Izmit earthquake postseismic deformation and loading of the Duzce earthquake hypocenter[J].Bull Seismol Soc Am,92(1):172--193.
Hearn E H.2003.What can GPS data tell us about the dynamics of post-seismic deformation?[J].Geophys J Int,155(3):753--777.
Hearn E H,McClusky S,Ergintav S,Reilinger R E.2009.Izmit earthquake postseismic deformation and dynamics of the North Anatolian fault zone[J].J Geophys Res,114(B8):B08405.doi:10.1029/2008JB006026.
Hsu Y J,Simons M,Avouac J P,Galetzka J,Sieh K,Chlieh M,Natawidjaja D,Prawirodirdjo L,Bock Y.2006.Frictional afterslip following the 2005Nias-Simeulue earthquake,Sumatra[J].Science,312(5782):1921--1926.
Ismail W B,Mainprice D.1998.An olivine fabric database:An overview of upper mantle fabrics and seismic anisotropy[J].Tectonophysics,296(1/2):145--157.
Jackson J.2002.Strength of the continental lithosphere:Time to abandon the jelly sandwich?[J].GSA Today,12(9):4--10.
Jacobs A,Sandwell D,Fialko Y,Sichoix L.2002.The 1999(MW7.1)Hector Mine,California,earthquake:Near-field postseismic deformation from ERS interferometry[J].Bull Seismol Soc Am,92(4):1433--1442.
Johnson K M,Bürgmann R,Larson K.2006.Frictional properties on the San Andreas fault near Parkfield,California,inferred from models of afterslip following the 2004earthquake[J].Bull Seismol Soc Am,96(4B):S321--S338.
Johnson K M,Bürgmann R,Freymueller J T.2009.Coupled afterslip and viscoelastic flow following the 2002Denali fault,Alaska earthquake[J].Geophys J Int,176(3):670--682.
Johnson K M,Fukuda J.2010.New methods for estimating the spatial distribution of locked asperities and stress-driven interseismic creep on faults with application to the San Francisco Bay area,California[J].J Geophys Res,115(B12):B12408.doi:10.1029/2010JB007703.
Karato S.2008.Deformation of Earth Materials:An Introduction to the Theology of Solid Earth[M].Cambridge:Cambridge Univ Press:34--44.
Khazaradze G,Wang K,Klotz J,Hu Y,He J.2002.Prolonged post-seismic deformation of the 1960great Chile earthquake and implications for mantle rheology[J].Geophys Res Lett,29(22):7-1--7-4.
Kirby S H,Kronenberg A K.1987.Rheology of the lithosphere:Selected topics[J].Rev Geophys,25(6):1219--1244.
Kohlstedt D L,Evans B,Mackwell S J.1995.Strength of the lithosphere:Constraints imposed by laboratory experiments[J].J Geophys Res,100(B9):17587--17602.
Kreemer C,Blewitt G,Maerten F.2006.Co-and postseismic deformation of the 28March 2005Nias MW8.7earthquake from continuous GPS data[J].Geophys Res Lett,33(7):L07307.doi:10.1029/2005GL025566.
Lowry A R,Pérez-GussinyéM.2011.The role of crustal quartz in controlling Cordilleran deformation[J].Nature,471(7338):353--357.
Marone C J,Scholz C H,Bilham R.1991.On the mechanics of earthquake afterslip[J].J Geophys Res,96(B5):8441--8452.
Marone C.1998.Laboratory-derived friction laws and their application to seismic faulting[J].Ann Rev Earth Planet Soc,26(1):643--696.
Massonnet D,Thatcher W,Vadon H.1996.Detection of postseismic fault-zone collapse following the Landers earthquake[J].Nature,382(6592):612--616.
Masterlark T,Wang H F.2002.Transient stress-coupling between the 1992Landers and 1999Hector Mine,California,earthquakes[J].Bull Seismol Soc Am,92(4):1470--1486.
Nabarro F R N.1948.Deformation of crystals by motion of a single ions:In strength of solids[C]∥Report of a Conference on the Strength of Solids Bristol 7th--9th July1947 Physical Society.London:Physical Society:75--90.
Niemeijer A R,Spiers C J.2007.A microphysical model for strong velocity weakening in phyllosilicate-bearing fault gouges[J].J Geophys Res,112(B10):B10405.doi:10.1029/2007JB005008.
Nur A,Mavko G.1974.Postseismic viscoelastic rebound[J].Science,183(4121):204--206.
Owen S,Anderson G,Agnew D C,Johnson H,Hurst K,Reilinger R,Shen Z K,Svarc J,Baker T.2002.Early postseismic deformation from the 16October 1999 MW7.1Hector Mine,California,earthquake as measured by surveymode GPS[J].Bull Seismol Soc Am,92(4):1423--1432.
Ozawa S,Nishimura T,Suito H,Kobayashi T,Tobita M,Imakiire T.2011.Coseismic and postseismic slip of the 2011 magnitude--9Tohoku-Oki earthquake[J].Nature,475(7356):373--376.
Paul J,Lowry A R,Bilham R,Sen S,Smalley R Jr.2007.Postseismic deformation of the Andaman Islands following the 26December,2004Great Sumatra-Andaman earthquake[J].Geophys Res Lett,34(19):L19309.doi:10.1029/2007GL031024.
Peltzer G,Rosen P,Rogez F,Hudnut K.1998.Poroelastic rebound along the Landers 1992earthquake surface rupture[J].J Geophys Res,103(B12):30131--30145.
Perfettini H,Avouac J P.2004.Postseismic relaxation driven by brittle creep:A possible mechanism to reconcile geodetic measurements and the decay rate of aftershocks,application to the Chi-Chi earthquake,Taiwan[J].J Geophys Res,109(B2):B02304.doi:10.1029/2003JB002488.
Perfettini H,Avouac J P.2007.Modeling afterslip and aftershocks following the 1992Landers earthquake[J].J Geophys Res,112(B7):B07409.doi:10.1029/2006JB004399.
Pollitz F,Banerjee P,Grijalva K,Nagarajan B,Bürgmann R.2008.Effect of 3-D viscoelastic structure on post-seismic relaxation from the 2004 M=9.2Sumatra earthquake[J].Geophys J Int,173(1):189--204.
Pollitz F F.1992.Postseismic relaxation theory on the spherical earth[J].Bull Seismol Soc Am,82(1):422--453.
Pollitz F F.1997.Gravitational viscoelastic postseismic relaxation on a layered spherical earth[J].J Geophys Res,102(B8):17921--17941.
Pollitz F F,Peltzer G,Bürgmann R.2000.Mobility of continental mantle:Evidence from postseismic geodetic observations following the 1992Landers earthquake[J].J Geophys Res,105(B4):8035--8054.
Pollitz F F,Wicks C,Thatcher W.2001.Mantle flow beneath a continental strike-slip fault:Postseismic deformation after the 1999Hector Mine earthquake[J].Science,293(5536):1814--1818.
Pollitz F F.2003a.Post-seismic relaxation theory on a laterally heterogeneous viscoelastic model[J].Geophys J Int,155(1):57--78.
Pollitz F F.2003b.Transient rheology of the uppermost mantle beneath the Mojave desert,California[J].Earth Planet Sci Lett,215(1/2):89--104.
Pollitz F F.2005.Transient rheology of the upper mantle beneath central Alaska inferred from the crustal velocity field following the 2002Denali earthquake[J].J Geophys Res,110(B8):B08407.doi:10.1029/2005JB003672.
Pollitz F F,Thatcher W.2010.On the resolution of shallow mantle viscosity structure using postearthquake relaxation data:Application to the 1999Hector Mine,California,earthquake[J].J Geophys Res,115(B10):B10412.doi:10.1029/2010JB007405.
Royden L H,Burchfiel B C,King R W,Wang E,Chen Z L,Shen F,Liu Y P.1997.Surface deformation and lower crustal flow in eastern Tibet[J].Science,276(5313):788--790.
Rudnick R L,Fountain D M.1995.Nature and composition of the continental crust:A lower crustal perspective[J].Rev Geophys,33(3):267--309.
Ruina A.1983.Slip instability and state variable friction laws[J].J Geophys Res,88(B12):10359--10370.
Rundle J B.1978.Viscoelastic crustal deformation by finite quasi-static sources[J].J Geophys Res,83(B12):5937--5945.
Rundle J B.1980.Static elastic-gravitational deformation of a layered half space by point couple sources[J].J Geophys Res,85(B10):5355--5363.
Rutter E H,Elliott D.1976.The kinetics of rock deformation by pressure solution:Discussion[J].Philos T Roy Soc A,283(1312):203--219.
Rutter E H.1983.Pressure solution in nature,theory and experiment[J].J Geol Soc London,140(5):725--740.
Rybicki K.1971.The elastic residual field of a very long strike-slip fault in the presence of a discontinuity[J].Bull Seismol Soc Am,61(1):79--92.
Ryder I,Bürgmann R,Pollitz F.2011.Lower crustal relaxation beneath the Tibetan Plateau and Qaidam Basin following the 2001Kokoxili earthquake[J].Geophys J Int,187(2):613--630.
Savage J C,Burford R O.1973.Geodetic determination of relative plate motion in central California[J].J Geophys Res,78(5):832--845.
Savage J C,Prescott W H.1978.Asthenosphere readjustment and the earthquake cycle[J].J Geophys Res,83(B7):3369--3376.
Savage J C.1990.Equivalent strike-slip earthquake cycles in half-space and lithosphere-asthenosphere earth models[J].J Geophys Res,95(B4):4873--4879.
Savage J C,Svarc J L.1997.Postseismic deformation associated with the 1992 MW=7.3Landers earthquake,southern California[J].J Geophys Res,102(B4):7565--7577.
Scholz C H.1998.Earthquakes and friction laws[J].Nature,391(6662):37--42.
Shen Z K,Jackson D D,Feng Y,Cline M,Kim M,Fang P,Bock Y.1994.Postseismic deformation following the Landers earthquake,California,28June 1992[J].Bull Seismol Soc Am,84(3):780--791.
Shimamoto T.1986.Transition between frictional slip and ductile flow for halite shear zones at room temperature[J].Science,231(4739):711--714.
Thatcher W.1983.Nonlinear strain buildup and the earthquake cycle on the San Andreas fault[J].J Geophys Res,88(B7):5893--5902.
Thatcher W,Pollitz F F.2008.Temporal evolution of continental lithospheric strength in actively deforming regions[J].GSA Today,18(4):4--11.
Tse S T,Rice J R.1986.Crustal earthquake instability in relation to the depth variation of frictional slip properties[J].J Geophys Res,91(B9):9452--9472.
Vergnolle M,Pollitz F,Calais E.2003.Constraints on the viscosity of the continental crust and mantle from GPS measurements and postseismic deformation models in western Mongolia[J].J Geophys Res,108(B10):1--15.
Wang K,Hu Y,He J.2012.Deformation cycles of subduction earthquakes in a viscoelastic earth[J].Nature,484(7394):327--332.
Wang R J,Lorenzo-Martín F,Roth F.2006.PSGRN/PSCMP:A new code for calculating co-and post-seismic deformation,geoid and gravity changes based on the viscoelastic-gravitational dislocation theory[J].Comput Geosci,32(4):527--541.
Weertman J.1955.Theory of steady-state creep based on dislocation climb[J].J Appl Phys,26(10):1213--1217.
Weertman J.1970.The creep strength of the earth’s mantle[J].Rev Geophys,8(1):145--168.

