断层岩气体渗透率及Klinkenberg效应

段庆宝 杨晓松 陈建业

(中国地震局地质研究所，地震动力学国家重点实验室 100029)

0 引言

近年来一系列研究表明，流体在地震的孕育、发生及震后断层愈合等过程中均扮演着重要角色(Morrow et al.，1981;Sibson，1992;Rice，1992;Byerlee，1993;Caine et al.，1996;Evans et al.，1997;Bernabéet al.，1982;Faulkner et al.，2003;陈建业等，2012)。而断层带岩石的渗透率是理解流体与地震活动关系的主要物性参数(Miller et al.，2002)，是定量化研究地壳深部流体输运特性的基础。因此，精确测量断层岩渗透率在地震研究方面具有重要意义;并且在构造断层相关的地质资源、地质环境、地质工程等方面具有实际应用意义(陈颙等，2009)。

野外钻孔注水和实验室内测量是获取渗透率的两种主要方式。在实验室测量岩石渗透率通常是以气体(主要是氮气)或水为测量流体。相对于水而言，采用气体测量渗透率具有化学性质稳定、对环境因素敏感程度低、测量时间短等一系列优点(Freeman et al.，1983)，因此，实验室测量渗透率通常采用气体。而采用液体进行渗透率测量则容易受环境条件所影响，尤其是渗透率很低的样品，采用液体测量会延长测量周期，继而使得环境因素的影响更加显著。另外大量有关砂岩的实验结果表明，岩石的气体渗透率普遍高于液体渗透率(Heid et al.，1950;Jones，1972，1987;Faulkner et al.，2000;Tanikawa et al.，2009)。这主要是由于气体存在压缩性，其在多孔介质中的流动出现偏离Darcy渗流的现象所导致的。Darcy定律主要考虑了分子之间的碰撞，而忽略了分子和孔隙壁之间的碰撞。然而，当气体的平均分子自由程和岩石孔隙尺寸相当时，气体分子与孔隙管壁之间的碰撞频率显著地增加，孔隙管壁上的气体分子速度不再是0，这相当于给连续流附加了一项作用力。这种气体分子与孔隙管壁间的碰撞滑动称为滑脱效应，Klinkenberg在1941年首先实验研究了这种现象，因此亦被称为Klinkenberg效应，其气体渗透率公式为

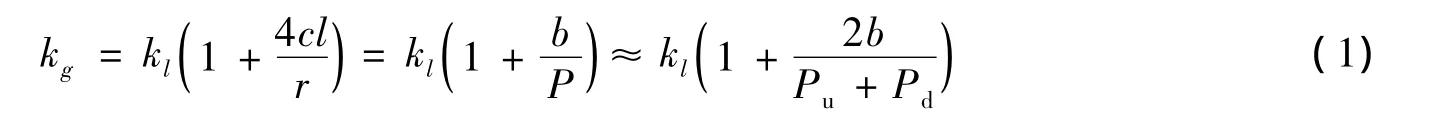
式(1)中:kg为气体渗透率;kl为绝对渗透率(或本征渗透率)，其定义为多孔介质在单相饱和条件下的渗透率，其值与测量采用的孔隙流体性质无关而仅与岩石骨架相关;c为常数因子(一般取0.9);l为气体的平均分子自由程;r为平均孔隙半径;P为孔隙压力，近似为上下游压力的平均值;b为滑脱因子(Pa)。从式(1)中可以看出，当孔隙半径r接近或小于气体的平均分子自由程l时，kg会远大于kl，表明滑脱效应强烈，不能忽略。滑脱因子由方程(2)表示

式(2)中:R为波尔兹曼常数，T为绝对温度。b值受温度和孔隙结构所控制。通常渗透率低的岩石b值大，Klinkenberg效应更为明显(Jones，1980)。Cosenza等(1999)讨论了盐岩中气体的平均分子自由程和气体压力的关系，认为当气体压力为0.06～6MPa时，其平均分子自由程与孔隙尺寸相当(10－7m2～10－9m2)，Klinkenberg效应比较显著。

目前有关Klinkenberg效应的实验研究主要是针对砂岩等沉积岩开展的(Wu et al.，1998;Zhang et al.，2001;Rushing et al.，2004;朱益华等，2007;陈卫忠等，2008;于丽艳等，2011)，鲜有涉及到断层岩的实验结果。因而人们对断层岩的Klinkenberg效应认识还很粗浅。由于渗透率越低的岩石Klinkenberg效应越强，而断层岩往往具有低渗特性(断层泥可达10－22m2)，其Klinkenberg效应不能忽略。本文以汶川地震断裂带中的断层岩为主要对象，定量研究了断层岩的气体渗透率和滑脱效应。结果对研究断层带岩石渗透性及气体渗透率校正提供了重要实验约束。此外，实验结果对于低渗透的油气藏开发、核废料处理等相关领域的研究也具有实际意义。

1 气体渗透率校正方法

由于气体渗透率测量结果比绝对渗透率高，所以实际应用中要对实测结果进行校正。常用的气体渗透率校正方法有实验数据拟合法、经验关系法和数值模拟法。1)实验数据拟合法是在一定围压下通过测量不同孔隙压条件下的气体渗透率，根据式(1)进行线性拟合求出绝对渗透率kl和滑脱因子b值。该方法所获的结果可靠、精度高，缺点是需要反复多次改变孔隙压力测量渗透率，其过程繁琐需要耗费大量时间。2)经验关系法是前人(Heid et al.，1950;Jones et al.，1980;Tanikawa et al.，2009)在大量实验的基础上总结得出的b与kl间的关系，其一般形式为。将该关系式代入式(1)，可得出绝对渗透率与气测渗透率间的关系。3)类似基于格子Boltzmann等方法的数值模拟(Liu et al.，2003;朱益华等，2007)。该类方法需要对样品孔隙结构及尺寸等做一定假设和简化。综上所述，实验数据拟合与经验关系法相结合是获得绝对渗透率的精确而又有效的手段。积累有关断层岩的实验数据对于研究断层带渗透性有重要意义。

2 样品与实验方法

实验选取了以断层岩为主的11个样品(表1)。其中断层岩样品采自汶川地震断裂带的一系列地表露头及汶川地震断裂带科学钻探1号孔(WFSD－1)。断层泥样品在野外直接用内径20mm的钢管钻取;角砾岩及围岩样品则是在室内从采集到的块状样品上钻取。为防止断层泥及碎裂角砾岩发生松散，样品外围用热缩管包裹。样品长度为10～20mm。样品两端磨平，实验前样品置于烘箱内，经80℃恒温72h以上烘干，使样品内的水分彻底散失以保证气体渗透率实验的准确性;同时在低温下烘干又避免了较高温度下黏土矿物的化学反应。

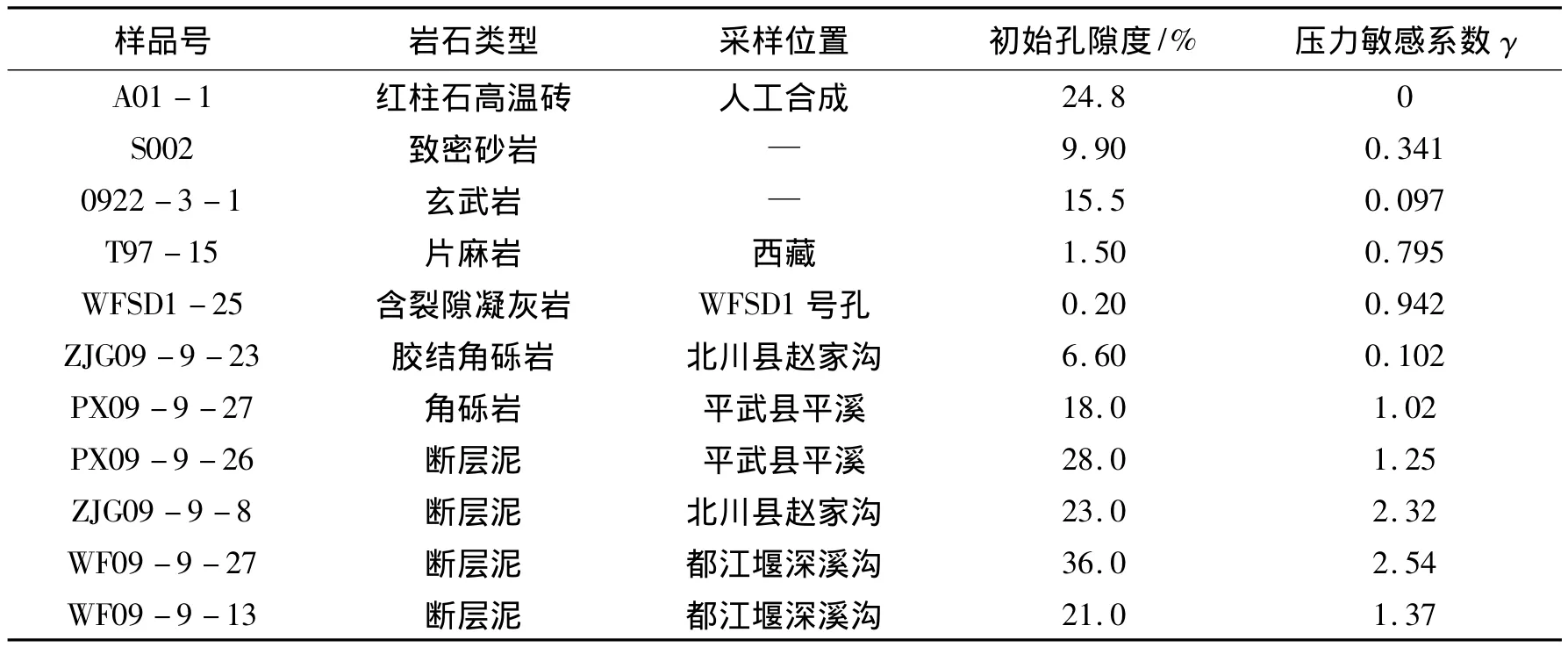
表1 实验样品参数及实验结果Table 1 Samples and experimental results

渗透率实验在地震动力学国家重点实验室GP－5岩石气体渗透率仪上进行。采用恒流法，N2为孔隙流体，气体流量采用标定过的孔板计量。实验设备的孔隙压范围是0～0.7MPa，围压范围是2～40MPa，实验装置如图1，其有效测量范围为5×10－20m2～4×10－11m2。实验时，将高渗砂岩(其渗透率＞1×10－11m2)置于实验样品两端，一并放入橡胶筒中，两端用堵头堵好(图1)。实验过程中首先加载围压至4MPa，在上游压力分别为0.250，0.289，0.395，0.560，0.683MPa的条件下分别测量渗透率，然后逐步加载围压的过程中分别重复上述测量步骤，至围压40MPa后开始卸载围压并测量渗透率。实际操作中，对于渗透率较高的样品，可以直接从流量计的中间水柱或水银柱高度读取压差来计算渗透率;对于低渗的样品(＜10－13m2)，读取背压水柱结合C值计算渗透率(具体计算过程参见陈建业等，2011)。

3 实验结果

气体渗透率实验结果如图2中左侧1列，右侧1列为对应的Klinkenberg校正。随围压加载，样品渗透率均逐渐下降;相比而言，断层泥样品的渗透率随围压升高而下降的幅度较大，角砾岩和结晶岩下降幅度较小。在围压由4MPa加载到40MPa过程中，断层泥样品的渗透率下降幅度达2～3个数量级，角砾岩和结晶岩的渗透率下降幅度基本在1个数量级之内。在40MPa围压下断层泥样品的气体渗透率为2.6×10－18m2～6.9 ×10－17m2，角砾岩气体渗透率较断层泥高出约1个数量级。对比加载和卸载围压过程中的渗透率发现，角砾岩与结晶岩相似，其渗透率差别较小;而断层泥的渗透率差别较大，即断层泥样品的渗透率在围压卸载过程中很难恢复。

在相同围压下，上游压力由0.25MPa逐渐变化至0.68MPa的过程中，样品渗透率均表现出对上游压力依赖性，即随上游压力升高渗透率逐渐下降(图2)。断层岩的气体渗透率随2/(Pu+Pd)的变化均为线性正相关(图2)，这表明气体渗透率测量存在明显的Klinkenberg效应。将上、下游压力的平均值近似为孔隙压力的情况下，即可经式(1)回归得出绝对渗透率和滑脱因子。将实验结果按照式(1)进行了线性拟合，得出了绝对渗透率kl和滑脱因子b值(图2，表2)。绝对渗透率kl均低于实测气体渗透率，并且其降低的幅度具有随围压升高而增大的趋势，即高围压下的气体渗透率与绝对渗透率之差较大。随着围压升高，样品孔隙逐渐关闭，孔隙度减小，绝对渗透率逐渐下降，同时滑脱效应增强，b值逐渐增大(图3)。

图4中实心符号代表本文(最高压力40MPa，孔板计量气体流量)的实验结果，其中实心圆代表断层岩，实心菱形代表结晶岩。空心符号是引入的3个样品在高围压(最高压力180MPa，皂膜流量计计量气体流量)下的实验结果(段庆宝等，2014)。将所有断层岩数据拟合得到了滑脱因子b值和绝对渗透率之间的关系，并与前人的研究结果做了对比。拟合得出b与kl之间符合幂次关系，与前人沉积岩结果相比，双对数图中的线性关系斜率更大，滑脱效应更强，断层泥(WF09－9－13)样品在高围压下的数据点滑脱因子更偏大，表明低渗的断层泥样品由于孔隙尺寸较小，气体测量渗透率时会伴随有强烈的滑脱效应。而砂岩S002的数据点与前人的沉积岩的实验结果走势基本一致，这可能也暗示了在低渗范围内，断层岩与沉积岩的滑脱效应具有一定差别。

图1 恒流法渗透率实验装样图Fig.1 Sample assemble of permeability experiment for steady state method.

4 讨论与结论

4.1 气体渗透率与Klinkenberg效应

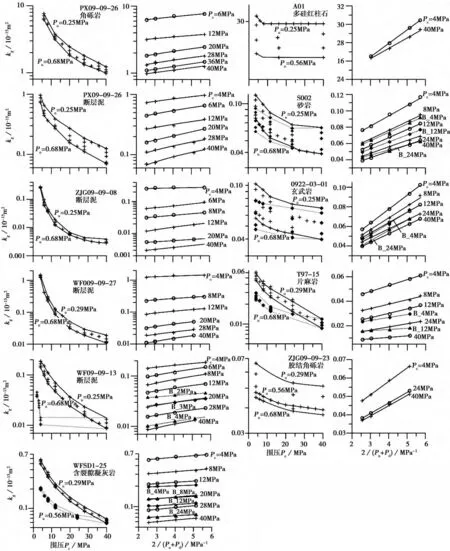
图2 实验结果及Klinkenberg校正Fig.2 Experimental results and Klinkenberg correction.

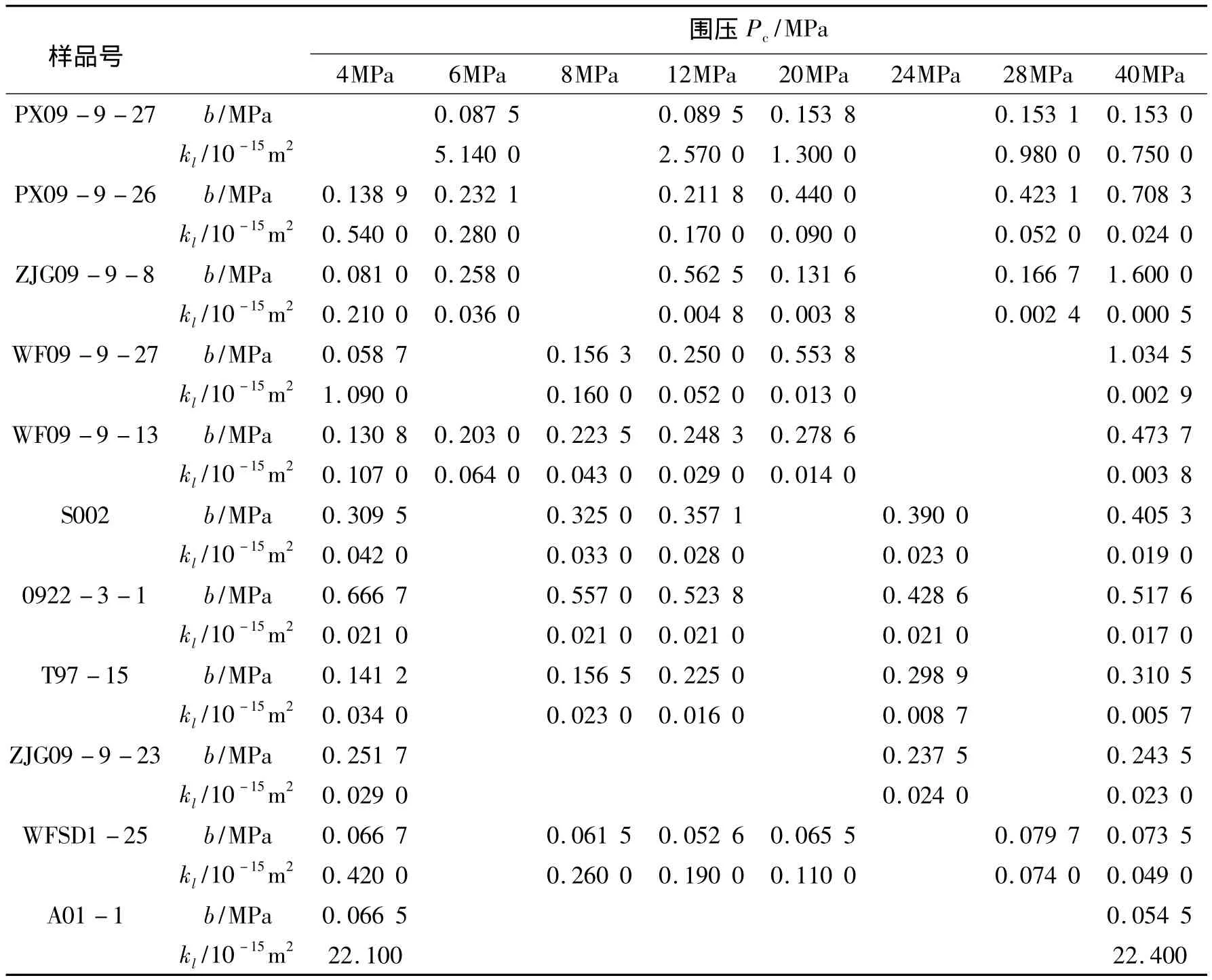
表2 绝对渗透率和滑脱因子拟合结果Table 2 Results of intrinsic permeability and slippage factor

本文实验样品的绝对渗透率集中在10－14m2～10－18m2范围内(表2)。在绝对渗透率与滑脱因子双对数图中，实验数据具有线性分布关系(图4)。此外，结晶岩的实验数据与断层岩的分布基本一致，表明在此渗透率范围内断层岩与结晶岩的气体滑脱效应强度基本一致。若计入在高围压(最高压力180MPa)条件下的测量结果(以空心符号表示，段庆宝等，2014)，其渗透率的分布范围下延至10－20m2，则断层岩在kl－b双对数图中线性分布的特点更为清晰。前人对具有不同孔隙度、不同渗透率样品，以及在双相孔隙流体等条件下对沉积岩样品进行了相关实验研究，其结果表明滑脱因子与绝对渗透率符合幂次关系(Heid et al.，1950;Sampath et al.，1982;Jones，1987;Rushing et al.，2003)。例如，Heid等(1950)研究了渗透率范围为10－12m2～10－17m2的岩心样品，得到 b=0.11kl－0.39的关系式;Jones等(1980)研究了渗透率范围介于10－14m2～10－19m2的低渗砂岩样品，得出的关系为b=kl－0.33;Tanikawa等(2009)研究渗透率范围为10－14m2～10－21m2的沉积岩样品得到b=(0.15±0.06)×kl(－0.37±0.038)的关系。利用最小二乘法对断层岩实验数据进行拟合得到的幂次关系。与前人的实验研究结果对比发现，其斜率绝对值明显大于沉积岩相应值。这暗示随着围压的增高，断层岩的孔隙尺寸减小得更快，滑脱效应更加明显(Persoff et al.，2001;Tanikawa et al.，2009)。本文幂次d值为0.476，明显大于沉积岩的d值(0.3～0.4)。d值越大则对应的滑脱因子越大，即Klinkenberg效应越强烈(尤其是在渗透率较低的区域内)。表明断层岩与沉积岩的滑脱效应存在差别，即断层岩的气体滑脱效应更强，这一现象可能与断层岩自身的矿物组成及孔隙结构有关。由于经历了地震破碎及水岩反应等过程，断层岩通常具有颗粒细小、裂隙发育、富含黏土矿物等特点，这些特性导致其与普通致密岩石的孔隙结构及渗流路径可能会有差异，如断层泥样品中可能会存在纳米尺度的微孔隙(Janssen et al.，2011)，这种细小的孔隙尺寸可能导致其Klinkenberg效应更强烈。

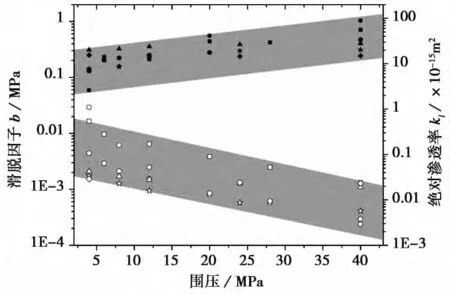
图3 滑脱因子和绝对渗透率随围压的变化关系Fig.3 Slippage factor and intrinsic permeability plotted as a function of confining pressure.

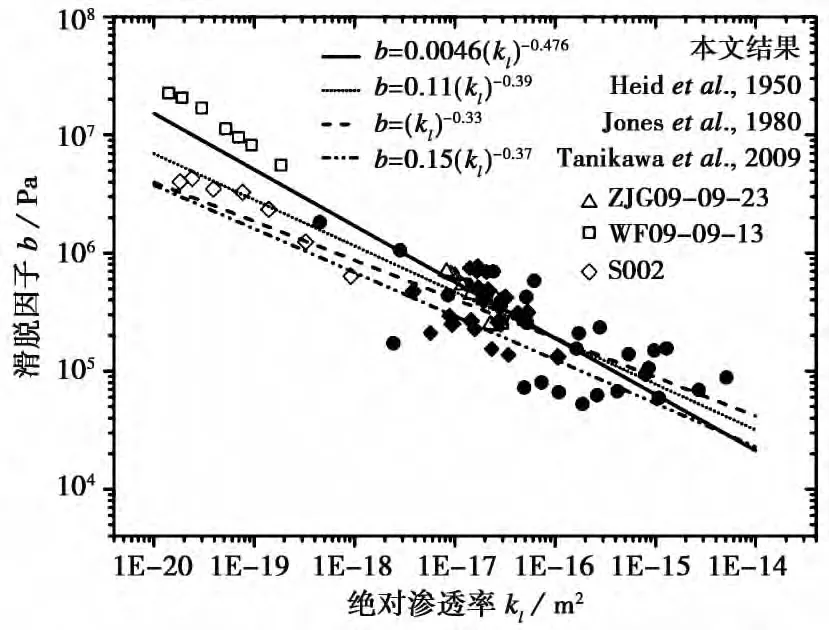
图4 滑脱因子b值和绝对渗透率的关系Fig.4 The relationship between slippage factor(b)and intrinsic permeability.

4.2 有效压力系数

随着深度增加，岩石所承受的有效压力增大，并导致岩石孔隙和微裂隙逐渐减小或关闭，其渗透率也随之逐渐降低。对不同的断层岩实验结果进行拟合即可获得渗透率随有效压力的变化关系，为推测深部断层带的渗透性提供依据。前人针对渗透率与有效压力的关系提出了不同描述方程，分别为幂次(Shi et al.，1986)和指数关系(Rice，1992;David et al.，1994)。由于本文实验所使用的孔隙压力较低(0～0.7MPa)，围压可近似为有效压力。对校正后的实验结果进行拟合，发现幂次关系，即k=k0(Pe/P0)－γ，能更好地描述渗透率与有效压力的关系。其中γ为压力敏感系数，k0为1个大气压下(地表)的渗透率(γ和k0由实验数据拟合得到);Pe和P0分别为有效压力和大气压力(1atm)。拟合结果表明，角砾岩及结晶岩的γ值较小，为0.1～1;断层泥 γ值较大，为1.25～2.54(表1)。不同的γ值反映了不同岩石的渗透率对围压的敏感程度不同。断层泥是以基质支撑为主，故在围压升高时，基质的压实作用相对明显，其渗透率下降较快，γ值偏大;而角砾岩及结晶岩具有颗粒支撑结构，在围压增高时颗粒对流体通道起到一定的保护作用(Wibberley et al.，2005)，故随围压升高，其渗透率下降相对缓慢，γ值偏小。

4.3 对断层带流体活动的启示

断层带核部的渗透率通常要比破碎带低很多(Chu et al.，1981;Morrow et al.，1984;Evans et al.，1997;Lockner et al.，2000;Mizoguchi et al.，2008)。本文实验结果显示，在40MPa有效压力下断层泥样品的绝对渗透率为 4.54×10－19m2～2.43×10－17m2，角砾岩的绝对渗透率较断层泥高出1～2个数量级，为2.25×10－17m2～7.94×10－16m2，显示核部低，两侧破碎带高的现象。该渗透率结构特征可用Caine等(1996)提出的“通道/障碍体”二元系统解释。这种渗透率分布结构决定了断层带流体容易在破碎带内流动，流体渗流主要集中在断层核部与围岩所夹的两侧破碎带内，从而倾向于平行断层面迁移(Morrow et al.，1992;Lockner et al.，2000)。断层带核部的低渗－超低渗特性有助于同震热压的发生和断层扩展(Sibson，1973;Andrews，2002;Wibberley et al.，2005;Rice，2006;Bizzarri，2006;Chen et al.，2013a，b)。

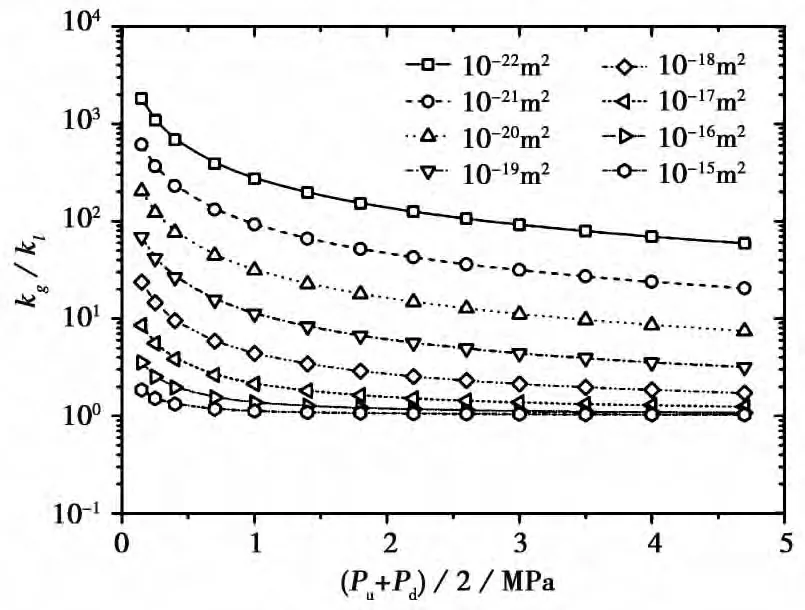
图5 气体渗透率与绝对渗透率之比随上下游压力平均值的变化Fig.5 The ratio of gas permeability to intrinsic permeability plotted as a function of the averaged pore pressure.

5 结论

对汶川地震断层岩进行了气体渗透率实验，结果显示断层岩气体渗流具有明显偏离Darcy渗流的现象，即渗透率随孔隙压的升高而逐渐降低。气体滑脱效应(Klinkenberg效应)可以解释该现象。断层岩的滑脱因子b值与绝对渗透率之间符合幂次关系，b=0.004 6kl－0.476。在超低渗透率范围内，断层岩的气体滑脱效应具有增强趋势，且显著偏离碎屑沉积岩的气体滑脱效应。利用气体作为孔隙介质测量断层岩的渗透率，必须进行Klinkenberg效应校正。实验结果对断层岩气体渗透率校正提供了依据，具有理论和实际应用意义。渗透率结果同时表明汶川地震断层带具有核部低、破碎带高的渗透结构，断层带核部具有热压作用发生所要求的低渗特性。