基于风场AGC调度控制的三区域控制法

李振华，曹积欣，董玲玲

(山东华能莱州风力发电有限公司，山东 264000)

0 引言

为提高风电并网运行的技术和管理水平、优化风电并网调度运行，为实现风电功率预测预报为辅助手段的各类电源协调运行、提高调度能力的具体目标，电力调度机构要按照有关法律法规和技术标准要求，加强风电调度管理，在保证电力系统安全稳定运行的前提下，实现风电等可再生能源的优先调度和全额收购目标要求。

因此风电场必须具备低电压穿越技术，风场负荷预测系统、风电场在线负荷控制技术，风电场在线负荷控制技术主要控制的是完成电力调度机构对风场下发的负荷目标进行有效的目标跟踪控制，将负荷控制稳态、无差地运行在目标状态之中，即风场统称的AGC调度运行控制。

1 三区域控制法

对于风电场在线负荷控制技术，可以认为是实现最优控制，控制的准则是指满足 JITAE为最小的控制方式，可采用表达函数为:

其中e(t)为控制和目标的偏差，τs为过渡时间[1]。

由于风场的风速具有随机性，风速的变化相对规律比较难于预计，同时短期风速的变化不会太大，因此系统的误差过渡跟踪时间是可以根据风速的变化趋势范围加以定性控制的，不同的风速范围变化决定不同的系统过渡控制时间常数，通过优化修正控制确保系统的稳定性和鲁棒性，具体的系统控制如图1所示。

图1 系统控制结构图

2 控制策略

2.1 经典PID区域控制

对于目标给定功率和实际功率值之间采用经典PID控制，经典PID着重于系统输出量，根据当前时刻的误差量(P)，误差累计量(I)以及误差的变化速率(D)来调整输入量[2]。

经典PID的传递函数采用:

其中Kp代表比例增益，Tn为积分时间常数，Tv及Td代表微分时间常数。

通过PID可以得到给定值和实际功率之间的目标调整趋势，但是由于直接使用却无法描述风速扰动误差对于趋势的影响，无法判断风机机组实际运行扰动误差对于趋势的影响。

2.2 优化区域控制

对于风场的AGC控制目标是整体场功率的控制，整体功率取决于在风场中各个单体机组的发电功率累加和，由于单体机组所处的地理位置不同，所得到的风速和发电功率也各有偏差，对于单体机组的运行阶段大致分为:机组准备阶段、机组并网阶段、发电阶段、停止发电阶段，其中只有发电阶段机组对外输出有功功率，其余阶段均不输出。机组准备阶段、机组并网阶段代表机组在正常运行模式，停止发电阶段代表机组存在故障保护停机。

因此总结风场的扰动误差包含:

(1)风速的扰动，包含平均场风速扰动和机组风速扰动

(2)机组的运行模式对于功率的扰动

(3)采集数据的延时及通讯故障对于功率的扰动

为克服扰动量对于功率输出趋势的误差，需对控制模型加入对于扰动量的优化控制，确定扰动量的动态过渡时间和扰动幅度趋势，可以依据最优控制方式得到扰动的动态时间和趋势，可遵循以下函数:

其中ω的频率系数设定可通过风速变化趋势模型得到不同的系数比例值，β1和β2的系数取定于机组的运行模式和通讯模式联合判断函数。

通过优化控制区域，我们可以对功率输出趋势进行有效的误差修正，保证趋势的变化是在可控制的范围内，所有误差的扰动将被取消。

2.3 机组输出区域控制

对于整体的功率输出趋势并不代表单台机组的功率控制目标，由于机组的地理位置、运行模式、机械特性等不同，需对机组进行有效的功率控制目标分配。

目前变速风力发电机组受到了很大的重视，它能根据外界风速的变化而调整风机转速，以达到捕获最大风能或实现输出稳定功率的目的[4]，双馈的变桨机组是目前使用最广泛的变速风力发电机组。

对于通过变桨模式在维持机组发电功率的平衡[5]，通过一个非线性化风机模型和一个桨距角控制器得到实现，因此可以得到双馈的变桨机组基础控制模式可以完整建立功率平衡控制。

对于双馈的变桨机组，其风能捕获功率、桨距角和发电机发电功率描述可遵循以下函数:

(1)捕获的风能功率

P0为捕获的风能功率，ρ空气密度，A为风轮的扫风面积，V为风速，Cp(λ)为Cp－λ曲线的取值。

λ为系统的叶尖速比，其函数:

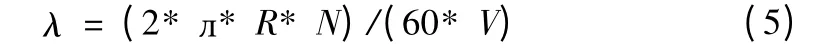
V为风速，R为为叶轮直径。

叶轮叶尖速和Cp和桨距角的曲线关系如下图2所示，图中只描述桨距角0－10°的曲线。

图2所示，X轴为λ，λ为无量纲数值，Y轴为Cp，Cp为无量纲数值。桨距角度对应的曲线标志在图上，从此得到结论是，风力发电系统捕获风能的能力不仅受其机械特性有关，还与所采用的控制策略有关[5]。在任何风速情况下，可以通过控制桨距角变化在保证捕获的风能功率恒定，其最优状态是目标风速和桨距角0°重合，大于目标风速桨距角通过变大趋势，通过新的λ和对应角度曲线Cp，通过Cp的变化来保证捕获的风能功率恒定。

图2 Cp-λ曲线

(2)对于固定的双馈机组，发电机功率曲线是固定的，图3所示为实际机组的发电机功率曲线

图3 发电机速度功率曲线

图3 中X轴为发电机功率(kW)，Y轴为速度(r/min)，从曲线中可以知道每一点的发电机速度只有一个对应的发电功率，双馈机组叶轮和发电机直接通过一个增速齿轮箱刚性连接，因此可以得到每一点的叶轮速度对应一点发电功率。

(3)对于固定的双馈机组的风速功率曲线是固定的，图4所示为实际机组的风速功率曲线

图4 中X轴为风速(m/s)，Y轴为风功率(kW)，从曲线中可知每一点的发电机速度只有一个对应的发电功率，双馈机组叶轮和发电机直接通过一个增速齿轮箱刚性连接，因此可以得到每一点的叶轮速度对应一点发电功率。

综合上述，对应一个投入运行的双馈机组，每一点的风速对应一个固定的叶轮速度，固定的发电功率;在对应风速度点上可以通过设定不同的叶轮速度，通过变桨控制将速度和功率恒定在一个固定区域内，最大的速度调节范围不能超过此点的风速点对应的功率，最小的功率范围可以是系统有效的最小发电功率所对应的叶轮速度，因此可确定的机组AGC调整控制范围为:

Pout为输出功率，Pwind此风速点的额定功率，Pmin为系统最小额定发电功率。

由于机组存在一定的振动状态[6]，对机组的振动状态进行定量分析，此系统必须具备振动穿越控制保护，一般而言系统的振动区域在一个固定范围，系统必须具备在AGC模式下穿越振动的功能。

3 实现方式

在实际风场采用上述控制策略方式时，通过C++作为实现控制方式的软件体系及通讯采集的协议转换体系，服务器和通讯接收器组成的硬件体系，以39台双馈机组的风场为目标，建立一个AGC控制调整平台，通过实际的参数调整和控制修正，得到满意的运行结果，基本AGC的控制调整精度在2%，达到预期的控制目标。

4 结束语

三区域控制模式可以有效地运用于风场的AGC控制运行，由于风场的实际风况变化和风场所处于的类型不同，产生的风速扰动变量趋势会有较大的不同，因此对优化控制的参数设定需和实际风场相匹配，同时由于不同厂商机组的通讯模式和通讯效率各不相同，因此对三区域控制模式有效的控制循环周期需根据机组做相应的调整。总体上分析，采用三区域控制模式建立独立的AGC控制，具有相对控制稳定，硬件投入量不大的特点，具有广泛的应用前景。

[1]项国波.ITAE最佳控制[M].北京:机械工业出版社，1986.

[2]杨敏军，郑胜，马飞林.混流式水轮机组的模糊滑模控制[J].电气自动化，2013，35(3):6 －8.

[3]谢军，黄禹，龚时华，等.带阶跃扰动的无静差控制系统设计[J].电气自动化，2013，35(2):1 －3.

[4]何真，龚春英 变速风力发电机组全局快速Terminal滑模控制[J].电气自动化，2013，35(3):51 －53.

[5]耿华，杨耕变速变桨风电系统的功率水平控制[J].中国电机工程学报，2008，28(25):267 －270.

[6]姚兴佳，刘颖明，刘光德 .大型风电机组振动分析和在线状态监测技术[J]，沈阳工业大学学报，2007，29(6):627－632.