基于加权移动平均法的常用药品短期采购需求预测及应用

刘 慧

（南京市鼓楼医院，江苏 南京 210009）

0 引言

现阶段，南京市鼓楼医院及国内各主要医疗机构中，药品采购计划的制作主要有人工制定和按照库存上下限生成2 种方式。但无论哪种方式，均需要富有经验的采购人员进行大量的人工干预（库存上下限需要人工设定），在给人员增加了额外工作负担的同时，过于依赖人员的个人经验，使采购过程存在一定的波动性和不确定性。本文将在保障临床药品供应的前提下，就医疗机构中各常用药品的自动化采购过程进行探讨。

1 问题定义与推导

1.1 问题的定义及评价标准

在医院实际运作中，存在大量不同类型的用药采购需求，如临床特需用药、节假日备药、突发事件紧急用药等。本方案重点针对临床广泛使用的常用药品品种，在暂不考虑突发公共卫生事件的情况下，以保障临床使用为基本前提，尽可能减少库存压力、人员工作强度、采购过程成本。

基于上述内容，本方案问题的解决情况可由如下标准进行判定：

（1）在库的库存数量始终略大于或等于本采购周期内前端现场的消耗总量（采购消耗比略大于1）。（2）特定品种药品历次采购数量和间隔周期保持相对稳定（历次采购数量标准差较小）。（3）本方案实施后，不可因本方案的实施额外增加药品的采购及配送次数。

假定：（1）院内库房向现场每天配送1 次（周末除外）。（2）院外采购每周至多2 次。

1.2 问题推导

经过分析不难发现，在暂不考虑经济成本的情况下，临床用药现场的药品储备应保持相对稳定，其最高库存水平稳定在每个波动周期的峰值左右（基础库存）。而库房库存也应保持稳定，库存水平位于下个到货点来临前，满足全部的前端消耗。因此，采购量的计算问题简化为：如何准确预测前段消耗并设定基础库存，进而确定单位周期内的采购计划。

具体推导过程可归纳为：（1）以加权移动平均法预测并设定各临床前端基础库存Wi。（2）根据各前端基础库存Wi设定库房基础库存S。（3）通常情况下，库房库存Q 采用设定库房库存系数k 的方式进行计算。例如，当Wi为某药房1 天用量，而采购到货周期为3 天，则k 应不小于3。具体数值设定视医院库存管理要求而定。（4）采购时，优先补满前段基础库存，使其在库量等于基础库存，然后补满库房基础库存。（5）采购量Q可由公式计算得出：Q=（S-S′）+∑（Wi-Wi′）。其中，S′，Wi′分别为库房和临床前段当前药品在库。

2 数据预测及监控

2.1 数据来源与分析

统计数据来自于本院各科室预测前3 个月实际已发生的消耗数据。本文数据以2013 年1-4 月的各科室最常用的药品消耗数据进行算法示意，并以2011 年和2012 年同期未采用本方法进行采购时的数据进行实际效果对比检验。

（1）本方法中，临床前段的用药需求预测是计算采购量的核心，本文以本院各科室使用广泛且用量较大的10 种药品为例，药品分类涉及口服、注射、外用等，统计时间2013 年1-4月为试验期，并以未采用本方法的2011 年同期和初步尝试采用本方法的2012 年数据进行实际效果对比检验。

（2）经过简单统计可发现，本院的药品消耗情况存在明显的周期性，以本院A 药为例（见图1）。

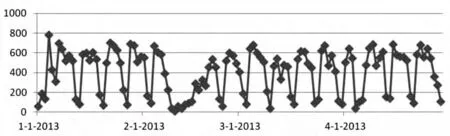
图1 A 药品2013 年1-4 月日消耗量走势图

从图1 中可发现，除2013 年春节期间外，本院药品消耗数据以周为单位呈周期性变化，且1 周内的波动幅度极大。而与之不同的是，各周期内同一时间节点（如每周一）的数值分布相对集中，如图2 所示。

图2 门诊药房A 药品周一消耗数据

可见，除2013 年春节（2 月11 日和2 月18 日）和五一（4月29 日）长假期间出现了异常点外，其他数据点的分布集中度明显优于按照日历日的排布数据分布。因此，在进行移动平均计算时，并不采用传统的日历日时间序列预测方法，而是将每周7 天的药品消耗数据分开统计，然后以该药品临近周次周一的消耗数据对下一周周一的消耗需求进行预测（周二至周日计算方式相同）。因春节等黄金周期间，受传统观念影响，患者就医人数和药品消耗量变化十分特殊，后文中进行预测计算时将暂不考虑此类影响。

（3）以本院广泛使用的某B 药品为例，以加权移动平均法对其下一阶段的消耗数据进行预测及检验。经过计算机多次模拟实验，选择移动平均的步长为3［1］，3 次移动平均的权值分别为0.15，0.3，0.55。

同理，将周一至周日全部数据进行计算，并将预测曲线与实际值曲线进行比较（见图3）。

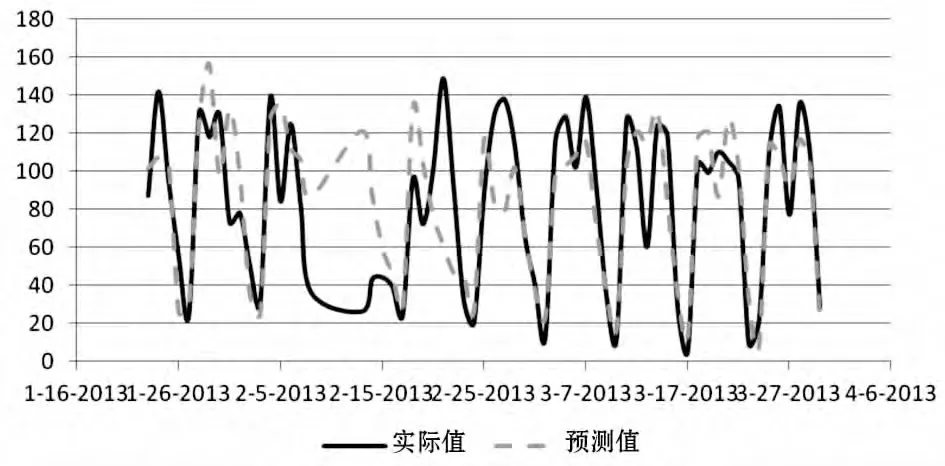
图3 3 个月内B 药品预测值与实际值偏差对比

表1 历次周一B药品消耗数据及预测误差分析

从图3 中不难发现，除少数奇点外，大部分预测值与实际值偏差较小，MAD 大多数情况下保持在15～20 之间，而其中波动较大的时间段（2013 年2 月5 日—2013 年2 月15 日）为春节特殊时期，暂不考虑。其他时间段预测误差均在可接收范围内。且通过上图可以发现，随着历史数据的积累，预测曲线与实际曲线存在相互靠近的趋势。

2.2 预测监控

预测过程中一个十分重要的理论基础就是：一定形式的需求模型过去、现在、将来都起着基本相同的作用。然而，实际情况经常会出现突然的变化。此时模式是否依然有效，则要通过预测监控来进行。

所谓跟踪信号（Tracking Signal）是指预测误差滚动和（RSFE）与平均绝对误差之间的比值，其计算公式为：

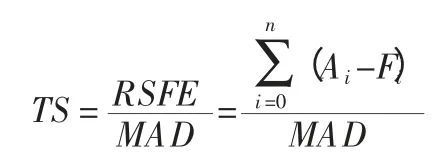
将表2 中的数据带入该公式可计算得出表2。

根据需求信号控制界限理论［2］，真实值落在预测控制界限之间的可能性满足表3［3］。

由误差分析表中数据可发现，除个别点Tracking-Signal 绝对值达到2.3 外，其他值均＜1.5，基本满足本院现阶段的管理要求。

3 实际运用效果评估

因本院在采购算法实验期内，院内的业务规模、药房结构都发生了重大变化，无法简单采用库存金额库存周转率等传统方式检验运营成果。因此，采用消耗比及订单平衡度2 项指标来进行数据测算。

表2 历次周一B药品消耗数据及预测误差分析

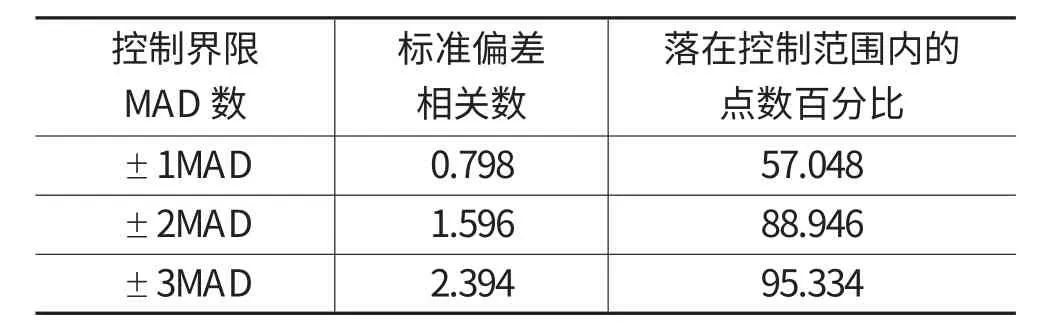
表3 控制界限

3.1 订单平衡度

订单平衡度指医院在向医院发起采购时，订单发出时间和采购数量基本稳定，有利于医院药品管理工作的平稳和供应商对医院服务水平的提升。此处以2011-2013 年度同期历次采购订单进行对比，计算其历次采购药品数量的标准差，若标准差呈下降趋势，则表示医院所发出的采购订单日趋平稳。具体结果如图4 所示。

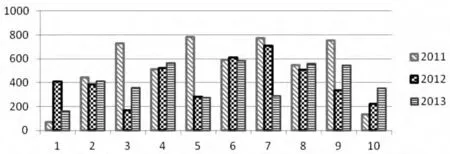
图4 2011-2013 年度同期常用药品采购数量标准差

由图4 可见，除个别品种外，医院历次采购数量标准差呈现明显下降趋势，这一现象表明随着本方法在医院的深入实施，对医院采购工作的平稳起到了积极的作用。

3.2 采购消耗比

从长远来看，抛开本算法运行初期残留的部分库存影响外，实验期内的采购数量与临床消耗数量的比值应接近但略大于1。以下以2013 年1-4 月间临床最常用7 种药品的采购消耗比监测数据为例进行说明（见图5）。

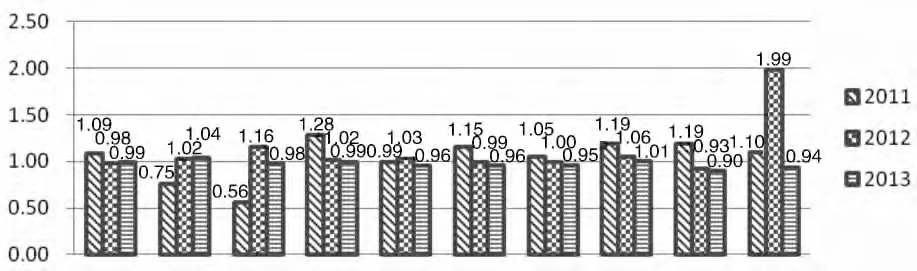
图5 2011-2013 年度同期常用药品采购消耗比

由图中数据可看出，本算法使用后，采购消耗比明显下降，此处所列举的7 种药品中平均降幅达13.15%，最高降幅达到了24.21%。

4 总结

移动平均法对医院常用药品的日常采购需求预测表现出了良好的效果，但对于春节等特殊时期以及部分非常用的品种预测的准确性仍有待提高。在后续的改进过程中，将逐步考虑引入其他统计学方法，针对其预测滞后等问题进行改良。

［1］段利忠，刘思峰，卢奇.移动平均法中移动步长的确定［J］.北京工业大学学报，2004（3）：378-381.

［2］陈敏.我国综合医院人流量预测模型的研究［D］.重庆：重庆大学，2012.

［3］陈启杰.市场调研与预测［M］.3 版.上海：上海财经大学出版社，2004.