基于博弈论的高职院校校企合作模式分析

吴 炜，张翠霞，路长国

（1.南通职业大学，江苏 南通 226007；2.南通市中等专业学校，江苏 南通 226011）

引言

我国高等职业教育可以追溯到19世纪中叶的洋务运动，但直到20世纪80年代才开始得到真正发展。进入21世纪，高等职业教育已经成为我国高等教育的重要组成部分。教育部关于推进高等职业教育改革与发展的若干意见指出，高等职业教育应走产学研结合发展道路，以提高质量为核心，合作办学、合作育人、合作就业、合作发展。然而由于高职教育社会认可度和影响力不高，校企合作困难重重，学校与企业的合作缺乏动力［1］。

在已有的研究基础上，本文认为高职院校校企合作过程中的问题和突出表现是企业与学校的合作动力不足，其主要原因在于与学校在合作模式和利益分配等方面存在矛盾。因此，本文在已有研究的基础上，基于博弈论中的相关理论，从校企合作中存在的问题出发，结合专业特点，探索问题的根源，提高校企合作的成功率和效益。

1 校企合作博弈模型

学校和企业分属于两个不同的行业，在校企合作中，高职院校和企业的利益诉求不一样，但都有为对方提供服务而获得更大利益的能力。企业（以4S店为例）可以参与高职院校学生和培养标准课程体系的建设，接受学生到企业实习和工作。同时，高职院校也可为企业输送掌握高技能的学生、培训员工、提供专业检测设备等。如果高职院校与企业能够实现有效的合作，提升高技能人才的培养层次和水平，高职院校和企业的合作就可以获得双赢。但在实际的合作过程中，合作双方都是理性经济人，都会根据合作过程中所获利益的多少来考虑在下一步合作中为对方所提供的服务。因此，本文从博弈论的角度出发，将合作双方作为理性经济人，研究合作双方的利益分配。

1.1 模型背景及假设

与现在需求决定供给的典型市场经济特征一样，在绝大多数校企合作案例中企业占有主导地位。以汽车检测与维修专业为例，高职院校培养的学生是掌握一定理论知识和技能的通用型人才，而4S店需要的是能快速熟悉和对本品牌车辆进行维修的专业技能人才。因此，企业需承担对学生的再培训所损失的利润和培训后人才流失的风险。在校企合作中，一般是企业先行动，提出诸如订单班等方式的合作。因此，在校企合作博弈中，企业先行动恰好反映了这一客观事实，这是博弈模型的假设前提［2］。

合作中的企业用C表示，学校用U 表示，双方都有合作的可能。

1）假设校企合作博弈中先由企业C 选择是否和学校U 合作，然后学校U 选择是否同意；如果学校U 同意合作，则合作双方协商有关期望利润的分配比例。

2）企业作为先行决策者，有三种可选择的策略：第一种是通过内部培训培养适合本单位需要的技术人才。第二种是通过引进定向培训的学生，获得所需人才。这种策略可以使企业直接获得具备相关品牌汽车专业知识的学生，这在现行的行业环境中是可行的。但是，仅仅通过一次性引进相关技能人才不利于在车型快速更新换代的情况下人才培养体系的形成。第三种是与学校签订合作协议，形成战略合作关系，即对订单班的学员或其他技术人员进行持续的技术培训。合作关系的形成，将校企双方的资源和能力结合起来进行发展，并在合作中实现连续的人才培养合作体系。这种合作可以使企业在不扰乱社会关系的情况下获取专业技能人才，这是一种双赢的合作。

3）假设学生到企业工作后所得利益为V。用PC1表示企业不与高职院校合作而自行培训员工所获利益的概率。PC2表示企业接受学校的定向培训生后所获利益的概率。PC3表示与高职院校合作，实现连续发展所获利益的概率。

若企业与学校合作，合作双方在签订合作协议时需对合作的收益进行分配，假设企业C 的收益分配比例是r，那么高职院校的比例则是1－r。假设高职院校为企业培养定向就业的学生所获培养费为K。又假设高职院校不与企业合作，将通用型人才输送到用人单位所获利益的概率为PU，而PU与PC3相互独立，那么校企合作双方合作成功的概率为（PC3＋PU）－PC3·PU，用γ来表示。显然，γ大于PU或PC3，这说明校企双方合作可以提高成功概率。

4）假设学校培养的学生参加工作后各方所得利益总和是π，企业和高职院校各方面的能力双方都可预测和判断。且假设合作双方不存在道德风险。

1.2 模型建立及求解

若企业选择内部培训，则所获期望利益为PC1·π，而高职院校为0，即其支付向量为（PC1·π，0）。

若企业提出与高职院校合作培养定向就业的学生，而学校同意，则企业的期望利益为PC2·π－K，高职院校的期望利益为K；如学校拒绝合作，则企业的期望利益为PC1·π，而学校的期望利益为0。因此，策略组合（合作，同意）的支付向量为（PC2·π－K，K），（合作，不同意）的支付向量为（PC1·π，0）。

若企业选择与高职院校一起进行持续的合作，而学校同意，则企业的期望利益为r·γ·π，高职院校的期望利益为（1－r）·γ·π－V；若学校不同意，则企业的期望利益仍然为PC1·π，学校的期望利益还是为0。因此，策略组合（合作，同意）的支付向量为（r·γ·π，（1－r）·γ·π－V），（合作，不同意）的支付向量为（PC1·π，0）。

这一博弈的树状图如图1所示。

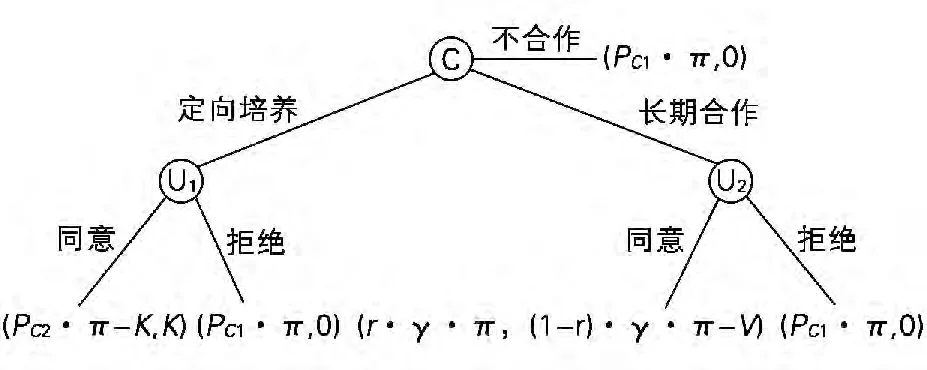
图1 校企合作博弈树

当企业提出与学校进行订单合作模式时，校企双方协商产生的培养费的讨价还价解需满足下式：

求上式的一阶条件，得纳什均衡解为［3］：

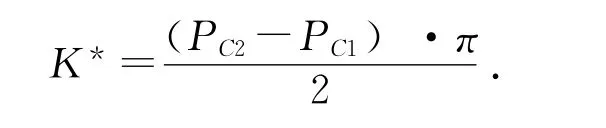
当企业提出与学校进行持续合作模式时，双方合作所得利益分配比例的讨价还价纳什均衡解需满足下式：

求上式的一阶条件，得纳什均衡解为：

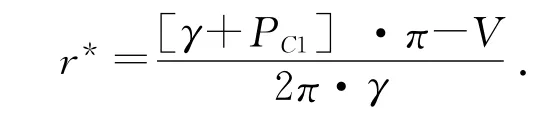
式中：γ＝（PC3＋PU）－PC3·PU。

2 模型分析

通过以上博弈分析可以得出以下分析结果：

1）对企业而言，若其PC2较高，则企业更愿意从学校接受订单班的学生，而不与学校进行持续合作。如果企业与学校合作，那么它更愿意与PU较高的学校合作。

2）对高职院校而言，学校的利益随PC1的提高而降低，随PC2、PC3的提高而提高。因此，学校更愿意与PC2、PC3高的企业合作。

3）合作的形成取决于企业的PC2、PC3而不是PC1，学校合作的愿望随着企业PC2、PC3的提高而增强，而且若V越大，越愿意合作。所以，合作的概率取决于V、PC3和π。

4）通过纳什的讨价还价均衡解，可以得到博弈分析的结果为（订单班，拒绝）和（持续合作，拒绝）的支付向量均为（PC1·π，0）；而（订单班，同意）的支付向量为，；（持续合作，同意）的支付向量为。

3 结语

本文从校企合作利益分配角度出发，结合高职院校的专业特点，将校企合作过程中利益分配视为博弈过程，运用博弈论的相关理论建立了校企合作的利益分配模型，得出了纳什均衡解。同时，探究了利益分配与概率、学生价值、总效益的关联关系，通过对模型的进一步分析，得出校企合作获得双赢的条件为。

值得注意的是，若企业的PC2越大，而PC3越小，则的概率越大，实现双赢就越不可能实现。这是因为如果高职院校培养的订单班学生自学能力很强，当企业接受这样的学生后其PC2会变得很大，自然其获取的利益会更多，而学校仍然只获得订单培养费，企业会转而选择与学校进行订单班合作模式。

［1］胡茂波，吴思.博弈论视野下高职教育校企合作的困境与对策［J］.教育与职业，2012（8）：11－13.

［2］公艳，王成军，窦德强.校企合作创新模式选择的博弈分析［J］.软科学，2009（4）：61－64.

［3］姚国庆.博弈论［M］.北京：高等教育出版社，2007.