基于CNOP方法的台风目标观测中三种敏感区 确定方案的比较研究

周菲凡 张贺

1 中国科学院大气物理研究所云降水物理与强风暴实验室，北京100029

2 中国科学院大气物理研究所国际气候与环境科学中心，北京100029

3 南京信息工程大学气象灾害预报预警与评估协同创新中心，南京210044

1 引言

目标观测是近一二十年新兴起的一种观测策略，它意图通过在一个小范围的区域内增加观测，使其与大范围增加观测对预报技巧有同等或相当的改善程度。因此，它的关键就是寻找这个小范围的观测区域，通常称之为敏感区。

目前识别敏感区有很多方法，这些方法的共同点是将一些“大值区”做为敏感区。这些大值区或是目标函数关于初始场的梯度的大值区（伴随敏感性方法，Baker and Daley,2000），或是快速发展的初始误差场的大值区（线性奇异向量方法，Palmer et al.,1998; 准反演线性方法，Pu and Kalnay,1999；繁殖方法，Hamill et al.,2000），或是观测增量的权重的大值区（集合转换方法，Bishop and Toth,1999；集合转换卡曼滤波方法，Bishop et al.,2001；集合卡曼滤波方法，Hamill and Snyder,2002）。

以“大值区”作为敏感区是有一定道理的。比如梯度场的大值区，表示在该地区给一个小扰动，会引起目标函数较大的变化，那么减小该地区的初始误差，可以减小预报误差，它的缺点是梯度技术是一种线性技术，用该方法识别敏感区的前提是线性近似是成立的；权重的大值区，表示该地区对使得预报误差极小具有重要的作用，它只有当样本达到一定数目时结果才有意义，样本数的选择成为关键的问题，同时理论上它也受到了线性近似的约束；而对于线性奇异向量（SV）方法、准反演线性方法等来说，它们主要的缺点也是采用了线性技术，受线性近似成立与否的约束，显然线性空间中最快发展不等于在非线性空间中最快发展。

为了克服线性近似假设的不足，Mu et al.（2003）提出了条件非线性最优扰动（CNOP）方法。CNOP是SV在非线性领域的一个自然推广，避免了线性近似假设的不足。该方法已被用于厄尔尼诺的可预报性与海洋热盐环流的敏感性分析（Duan et al.,2004,2008,2009; Mu et al.,2004,2007; Sun et al.,2005; Duan and Zhang,2010）、双旋海洋环流和斜压不稳定流的非线性行为的研究（Terwisscha van Scheltinga and Dijkstra,2008；Rivière et al.,2008），集合预报等的研究（穆穆和姜智娜，2007）。近年来，CNOP方法也被用于目标观测的研究，进行敏感区的识别，并取得了一系列可喜的成果（穆穆等，2007；Mu et al.,2009；Wang and Tan,2009; Tan et al.,2010; Qin and Mu,2011a,2011b; Zhou and Mu,2011,2012a,2012b; Chen and Mu,2012）。在上述研究中，敏感区是根据 CNOP的垂直积分能量而确定的，一般将CNOP的垂直积分能量的大值区作为敏感区，这与SV确定敏感区的方式（Buizza et al.,2007）相同。由于在上述研究中，存在有CNOP确定的敏感区同其他区域比对预报技巧的改善相当甚至不如的情况，因此也有审稿人曾对敏感区的确定方式进行了质疑。基于此，本文将深入考虑用CNOP方法确定敏感区的方式，比较几种确定方案得到的敏感区对预报的改善程度，最终给出用CNOP方法确定敏感区的较佳方案。

2 CNOP方法及其在目标观测中的应用原理

2.1 CNOP方法简介

考虑状态向量X的发展方程的初值问题：

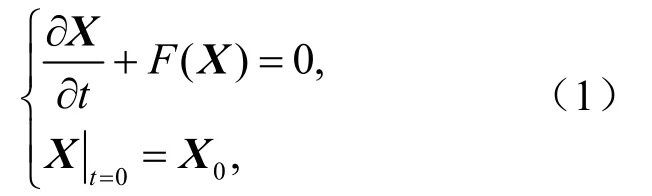
其中，F是一个非线性偏微分算子，X0为X的初始状态向量。方程（1）在预报时刻t的数值解可以写成如下的形式：

此处，M是离散的非线性传播算子。Xt为状态向量X在t时刻的非线性发展。初始扰动称为条件非线性最优扰动（CNOP）（Mu et al.,2003），当且仅当

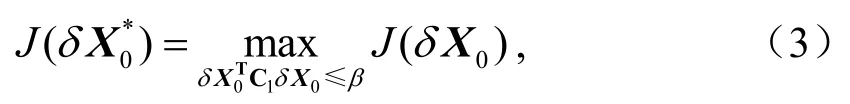
其中

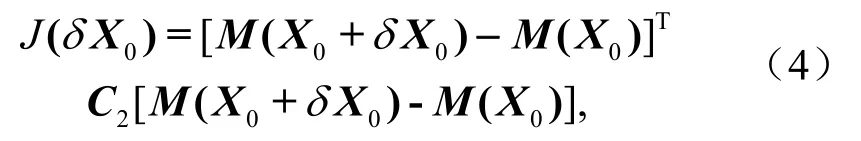
在某些情况下，目标函数（4）式可能存在局部极大值点，此时对应的初始扰动称之为局部CNOP。关于局部 CNOP的研究可见 Duan et al.（2004）。本文暂且不考虑局部CNOP。

本文中，约束值取β=0.03J kg-1，度量范数C1和C2都为干能量范数，即有

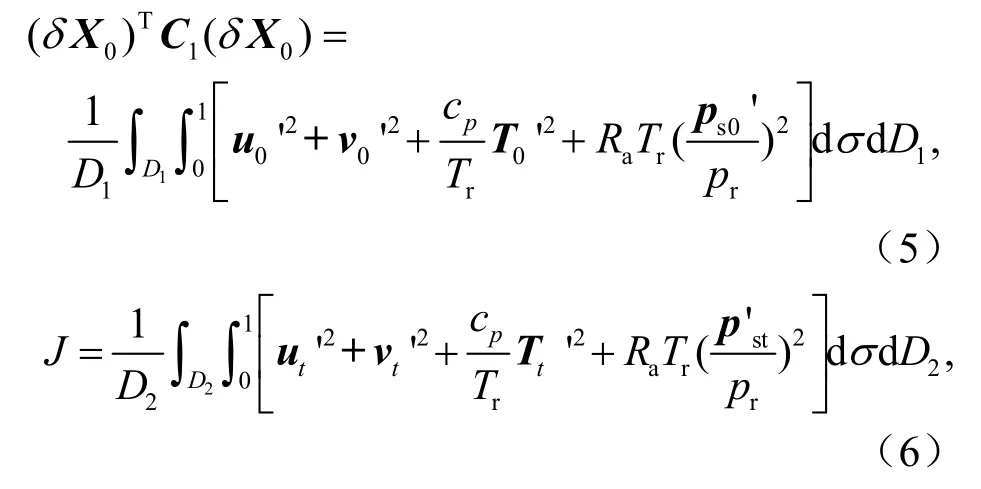
其中，D1为整个模式区域，D2为验证区域，σ为垂直方向坐标，cp=1005.71 kg-1K-1为定压比热，Ra=287.04 J kg-1K-1为干空气气体常数，另外，参数pr=1000 hPa，为δX0的分量场，非线性发展或线性发展而成的δXt的分量场，u'、v'、T'、ps'分别表示扰动场的纬向风分量、经向风分量、温度和地面气压。

2.2 CNOP在台风目标观测中的应用原理

将CNOP方法用于目标观测时，我们假设模式是完美的或模式误差相对较小，那么如果初始分析场具有CNOP类型的初始误差，则会导致最大的非线性预报误差。因此消除CNOP类型的初始误差，可以避免出现最差预报的情况，进而提高预报技巧。

在目标观测中，我们所关心的只是某一小部分地区（即验证区域）的预报技巧，这等同于在目标函数（4）式中加入一个投影算子P，该算子在验证区域内取值为 1，其他区域取值为 0，这就使得问题转化为只考虑验证区域的预报误差问题。此时，（4）式可写为

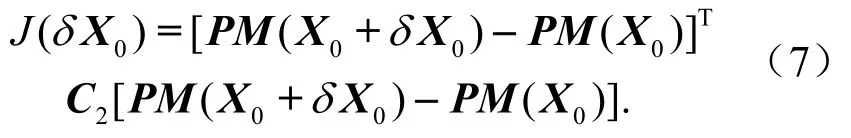
将目标观测思想与台风预报结合起来，那么就要求验证区域要尽可能包括台风在所关心时刻可能到达的区域，这样，如果提高了该区域的预报技巧，也就提高了该台风在所关心时刻的预报技巧。 在求得CNOP后，为提高预报技巧，我们要消除 CNOP 类型的初始误差。Mu et al.（2009）的研究表明，对CNOP型初始误差消除的程度越大，对预报效果的改善程度越明显，根据这一思路，我们将敏感区定义在尽可能最大程度地消除CNOP类型初始误差的地方。显然，在CNOP的大值区，可消除的误差程度最大。当然，这里需要指出，真实误差场的分布是未知的，可能是非CNOP类型的，但是CNOP却代表了导致最差预报技巧的一类初始误差，若是能够减小或消除出现最差预报的几率，预报技巧便能得到很大的提高。

3 用CNOP方法确定敏感区的几种方案的比较

3.1 方案介绍

由2.2节CNOP在台风目标观测中的应用原理可知，CNOP确定的敏感区应该是CNOP型初始误差的大值区。然而，CNOP型初始误差场可能并非单一的某个物理量的场，比如当选取干能量范数作为初始约束的度量时，初始误差场由温度场误差、风场误差以及地面气压场误差所组成，这时，温度场误差的大值区和风场误差的大值区以及地表气压的大值区可能并不重合，同时，即使对于同一个场，其大值区分布也可能是非连续的，即可能出现在某几个区域某几个层次上比较大，其他区域和层次都很小，即在垂直空间上出现了跳跃的情况。因此如果以所有物理量场的大值区作为敏感区，目标观测的实施将是比较困难的，同时要覆盖所有的大值区将会比较耗费物力和财力。因此有必要设计一种较优的方案，一方面既能尽可能包含误差大值区，另一方面又使目标观测较容易实施，当然最重要的是确实能使得预报效果有较大的改进。结合前人的研究，本文给出了三种确定敏感区的方案，通过比较，给出三种方案得到的敏感区的差异及其有效性。

方案一：水平投影方案。这一方案首先将CNOP的各物理量场①本文只考虑CNOP含有多种物理量分量场的情形，若只含有单一物理量场，则其大值区的水平投影即为敏感区。的大值区定义为它们的重要区 域，然后将各物理量场的重要区域重叠的部分作为整体重要区域，将整体重要区域在水平面上的投影确定为敏感区。由于本文中选取了干能量范数为初始扰动的度量范数，因此，这里CNOP的各物理量场有纬向风分量、经向风分量、温度和地面气压四个物理量场。

方案二：单点能量投影方案。这一方案首先计算CNOP在空间每一格点的能量，将能量大值区作为重要区域，将该重要区域在水平面上的投影确定为敏感区。

方案三：垂直积分能量方案。这一方案在计算完空间每一格点的能量后做垂直积分，从而得到水平面上每一格点所在垂直气层的总能量，将水平面上总能量分布的大值区作为敏感区。该方案即为目前常用的CNOP确定敏感区的方案。

由三种方案的定义可以看出，水平投影方案是比较“原始”的大值区，直接考虑各物理量场的大值区，它优点是简单明了，缺点是由于各物理量场的大值区很可能是部分重合的，如果只取重合的部分就可能漏掉了某些物理量场较大值所在的区域；单点能量投影方案由于计算了能量，事实上相当于对各物理量场乘以权重系数，因此可能使得某个物理量场的大值区被淡化，而另一个物理量场的大值区则被突出了，其优点是从能量的角度去度量，考虑的是每一格点上所有物理量场的综合作用，具备一定的物理意义；垂直积分能量方案相比于单点能量投影方案，进行了垂直方向上的累加，这有可能使得某些单点能量大，但其所在垂直层的其他层上能量小的这些格点被略掉，而层次能量分布均匀的看似“平凡”的格点被凸显出来。显然，它考虑的是整个层次的综合作用。由此可见，各种方案都各有优缺点，因此哪种方案更优，需要进一步分析其所确定的敏感区的有效性。

3.2 试验设计

本文使用的模式是宾夕法尼亚大学和美国国家大气研究中心（PSU-NCAR）共同开发的中尺度模式 MM5（Dudhia,1993）及其伴随系统（Zou et al.,1997）。其中，非线性模式采用的物理参数化方案主要有Anthes-Kuo积云对流参数化方案，高分辨率PBL方案，简单的辐射冷却方案和大尺度稳定降水。切线性及伴随模式采用与之相对应的但为干过程的物理参数化方案。优化算法选用有约束的迭代算法——谱投影梯度算法（SPG2,Birgin et al.,2001）。

选取了6个台风个例进行研究。2005年台风麦莎（Matsa）、2004 年台风米雷（米雷 1，Meari 1）、2010年台风鲇鱼（Megi）、2011年台风马鞍（Maon）、2011 年台风米雷（米雷 2，Meari 2）、2011年台风梅花（Muifa）。研究时段分别为： 2005年8月5日00时（协调世界时，下同）到8月6日00时（麦莎）、2004年9月26日00时到9月27日00时（米雷1）、2010年10月19日00时到10月20日00时（鲇鱼）、2011年7月18日12时到7月19日12时（马鞍）、2011年6月26日00时到6月27日00时（米雷2）、2011年8月1日18时到8月2日18时（梅花）。初边值由对应时段每 6小时一次的美国国家环境预测中心（NCEP）再分析资料插值到模式格点上而形成。分辨率取60 km，水平格点数除米雷 1为 51×55，其余均为55×55；垂直层数除了麦莎和米雷1为11层，其余均为20层，模式层顶都为100 hPa。

3.3 不同方案所确定的敏感区的差异

下面我们比较上述三种方案确定的敏感区的差异。

首先考查CNOP的分布形式，以麦莎和米雷1为例，进行分析。图1给出了这两个个例CNOP在850 hPa上的风场（矢量）和温度场（阴影）分量的大值区的分布图。由图可见，对于麦莎个例，CNOP风场大值区呈现出绕台风东北部及东南部区域的环状结构，温度场的大值区与部分的风场大值区重合，即也主要位于台风的东北和东南两个区域。同样，对于米雷个例，风场大值区也曾现出绕台风的环形区域，而温度场的大值区更主要地集中在初始台风的东北地区，和部分风场大值区重合。其余四个个例的结果显示，风场大值区也主要表现为绕初始台风的环形结构，温度场大值区则分为几个部分与部分风场大值区重合（图略）。这些大值区预示了敏感区可能所处的位置。

为便于比较，我们将三种方案确定的敏感区的大小取为一致。此外，又由于在目标观测中采用下投式探空仪增加观测是常见的手段，而一次观测过程中一般投送探空仪的个数为 10～20个（根据台湾 DOTSTAR 资料，Wu et al.,2005）。因此，我们假设要投送 20个探空仪，相应的，敏感区的大小定为20个格点，约占模式水平区域的0.7%。

仍以麦莎和米雷1为例，分析三种方案下的敏感区的分布形式。由图2可见，对于麦莎个例，水平投影方案下CNOP识别的敏感区主要集中在初始台风位置的东南偏南地区；单点能量投影方案下CNOP识别的敏感区表现为从初始台风位置的西北经东北到东南的地区，呈现为半环状；垂直积分能量方案下CNOP识别的敏感区主要集中在初始台风位置的西北和东北区域，东南区域也有两个格点；由此可见，单点能量投影方案和垂直积分能量方案下确定的敏感区比较相似，而与用水平投影方案确定的敏感区则具有较大的差别。

对于米雷1个例（图3），水平投影方案下CNOP识别的敏感区主要分为两部分：初始台风的东北地区，以及验证区域南部、初始台风的西南地区；而单点能量投影方案下CNOP识别的敏感区则主要位于初始台风的东北地区和北部地区；对于该个例，垂直积分能量方案下CNOP识别的敏感区也与单点能量投影方案下确定的敏感区较为相似，主要也位于初始台风的东北地区和北部地区，但在初始台风的西南区也有一小部分敏感区。

其他四个台风个例也显示，单点能量投影方案和垂直积分能量方案下确定的敏感区比较相似，而与用水平投影方案确定的敏感区有较大的差别（图略）。

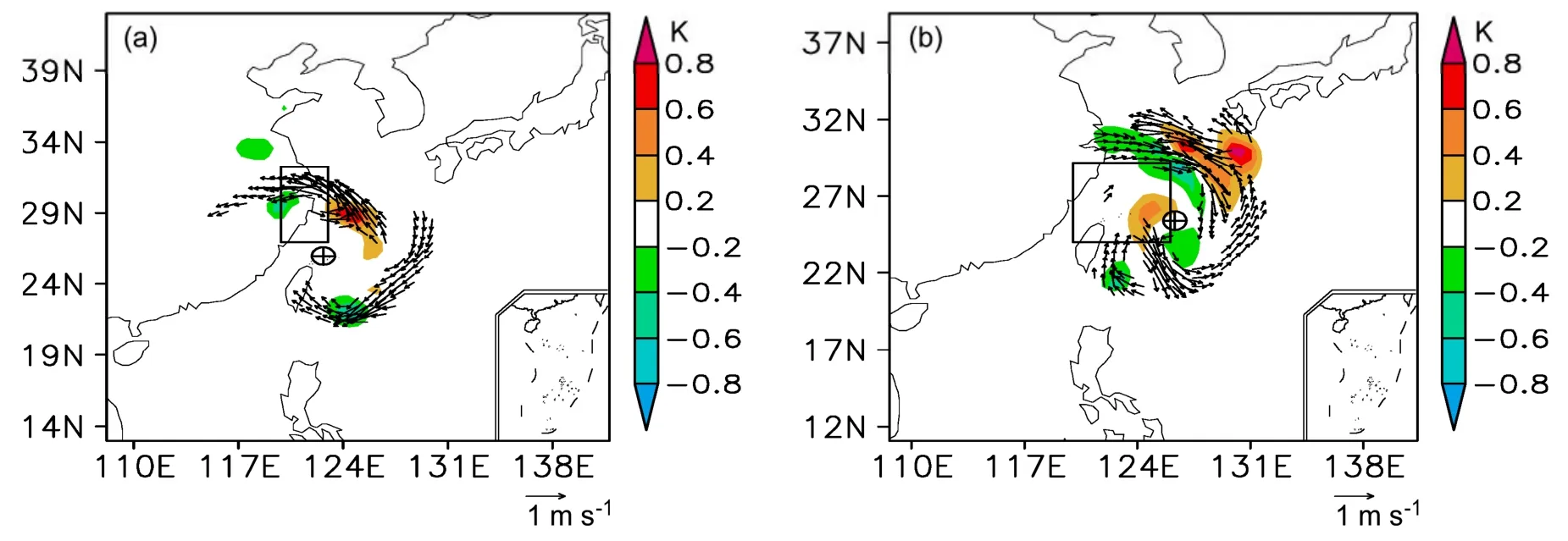
图1 CNOP在850 hPa上的风场（矢量，单位：m s-1）和温度场（阴影，单位：K）分布：（a）2005年台风麦莎；（b）2004年台风米雷。图中的矩形区域为验证区域，符号“⊕”表示初始时刻台风中心所处位置 Fig.1 The temperature(shaded,units: K)and wind(vector,units: m s-1)components of CNOP at 850 hPa:(a)Typhoon Matsa in 2005;(b)typhoon Meari in 2004.The boxes indicate the verification areas,⊕ indicates the position of the cyclone at initial prediction time

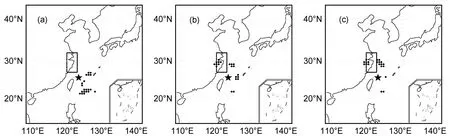
图2 麦莎个例：（a）水平投影方案、（b）单点能量投影方案、（c）垂直积分能量方案下确定的敏感性区域（用小圆点表示）。图中矩形区域表示验证区域，五角星表示初始时刻台风所在位置 Fig.2 The sensitive areas of Matsa identified by(a)horizontal projection scheme,(b)single energy projection scheme,and(c)vertically-integrated energy scheme.The boxes indicate the verification areas; the star indicates the position of the cyclone at initial prediction time

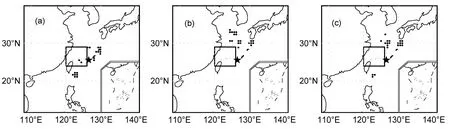
图3 同图2，但为米雷1个例 Fig.3 Same as Fig.2,but for Meari 1 case

综上，单点能量投影方案和垂直积分能量方案下确定的敏感区是比较相似的，这两种方案与水平投影方案确定的敏感区相比较则有较大的区别。

3.4 敏感区的物理意义分析

本小节将对各种方案下识别的敏感区的物理意义进行分析。

首先，考查影响台风发展变化的因子。前人的研究表明，影响台风发展变化的因子可以分为两大类，一类是环境场的影响（Chan and Gray，1982；孟智勇等，1998；Emanuel et al.,2004；李英等，2004），一类是其自身的结构特征的影响（Fiorino and Elsberry，1989；陈联寿等，1997；梁旭东等，2002；Corbosiero and Moinari，2003），当然还有这两类之间的相互作用。那么不同方案下识别的敏感区与这些影响台风发展变化的因子是否有着直接或间接的联系？基于此，我们将从台风的环流场配置以及台风的对流结构特征等方面着手考查敏感区的物理意义。由于单点能量投影方案下的敏感区与垂直积分能量方案确定的敏感区比较相似，因此这里我们将它们统称为能量方案，以下主要分析能量方案和水平投影方案得到的敏感区的物理意义有何区别。

首先分析能量方案下的敏感区的物理意义。

图4给出了麦莎个例基态初始场（2005年8月5 日 00 时）在 700 hPa、500 hPa 和 300 hPa 上的流场和温度场。对比图2可见，垂直积分能量方案确定的敏感区主要位于长江口处以及台风与西太平洋副热带高压的交界处，处于副高脊线的西南侧。在700 hPa上，该区域基本位于台风的气旋式环流中，其上的流场具有气旋式曲率，随着高度逐渐增加，该区域内的流场渐渐地从气旋式旋转过渡到反气旋式旋转，到 300 hPa，该区域已基本位于副高的反气旋式环流中，其上的流场具有反气旋式曲率。可见，垂直积分能量方案确定的敏感区上的 流场从低层到高层由气旋式曲率转为反气旋式曲率，即风场是随高度顺转的。此外由温度场和环流场的配置可知，该敏感区主要位于冷暖平流的交界区：在低层，主要表现为暖平流，冷平流较弱，随着高度的增加，暖平流逐渐减弱，冷平流逐渐加 强；在高层，冷平流作用则较为明显。同时由图 6可见，该敏感区内并没有明显的垂直运动。

再看米雷1个例。同样，我们也给出了其基态初始场（2004年9月26日00时）在700 hPa、500 hPa和300 hPa上的流场和温度场（图5）。对比图3可见，垂直积分能量方案下的敏感区也是位于台风和西太平洋副热带高压的交界地区，与麦莎个例不同的是，该个例中西风带明显较强且位置偏南，敏感区位于东亚大槽与副高的交界处，为三个系统相互作用的区域。在700 hPa上，一部分敏感区位于副高的反气旋式流场中，另一部分敏感区则位于台风的气旋式流场中，随着高度的增加，西风带南压，原先具有反气旋式曲率的流场逐渐被东亚大槽槽前的西南气流所取代，而原先具有气旋式曲率的流场则被南侧的副高的反气旋式流场所取代。可见，对于该个例，从低层到高层，垂直积分能量方案下的敏感区上的风场也是随高度顺转的。此外温度场和环流场的配置也显示，该敏感区也主要位于中层的冷暖平流交界处。由图6可见，该敏感区主要位于垂直运动的外围。

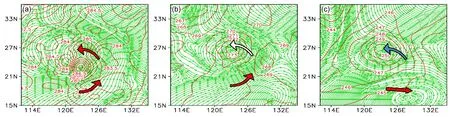
图4 麦莎个例。基态初始场在（a）700 hPa、（b）500 hPa、（c）300 hPa上的流场（绿色流线）和温度场（红色等值线）。红色箭头表示暖平流，蓝色箭头表示冷平流，白色箭头表示冷暖平流交界区 Fig.4 Matsa case.The stream lines(green)and temperatures(red)at(a)700 hPa,(b)500 hPa,and(c)300 hPa for initial basic states.Red arrow indicates the warm advection,the blue arrow indicates the cold advection,and the white arrow indicates the boundary of warm and cold advections

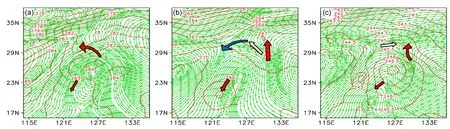
图5 同图4，但为米雷1个例 Fig.5 Same as Fig.4,but for Meari 1 case

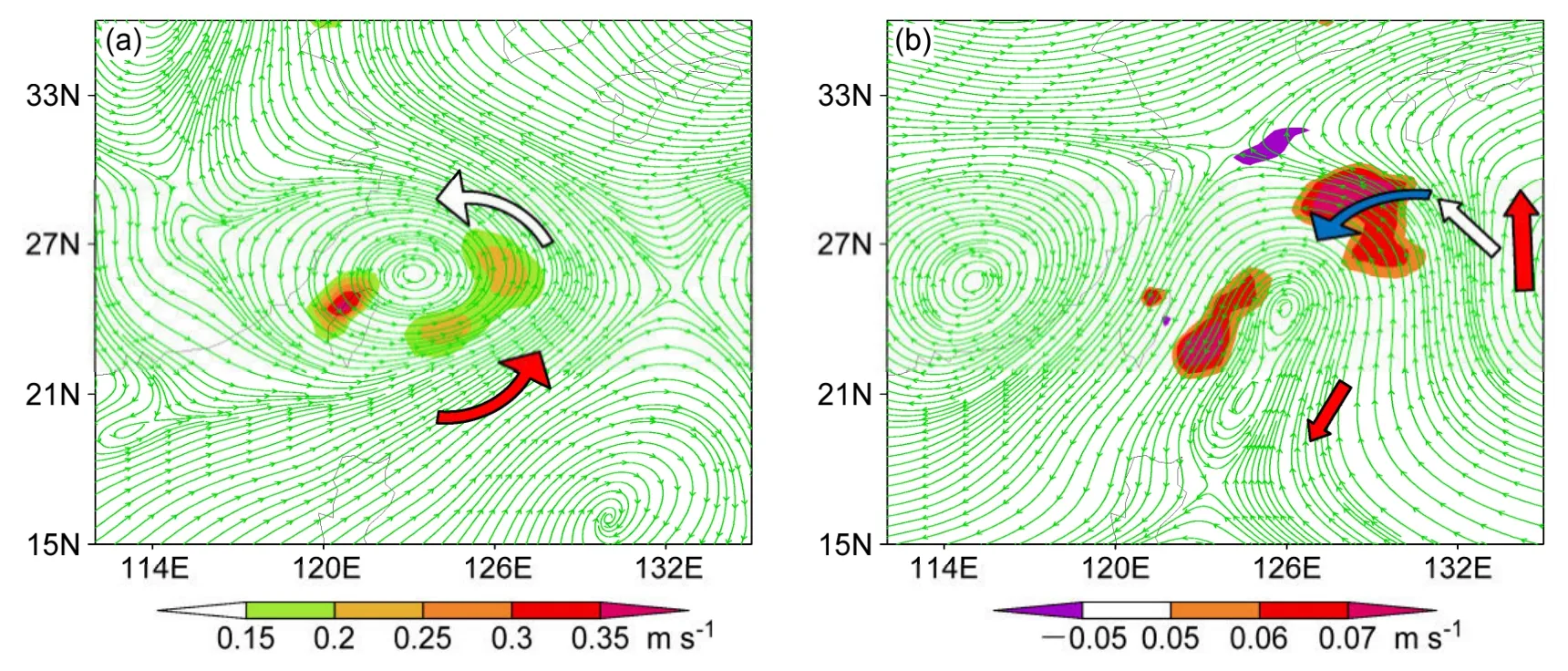
图6（a）麦莎、（b）米雷1的基本态初始场在500 hPa上的流场（绿色流线）和垂直运动（阴影，单位: m s-1）分布。红色箭头表示暖平流，蓝色箭头表示冷平流，白色箭头表示冷暖平流交界区 Fig.6 The stream lines(green)and the vertical motion(shaded,unit: m s-1)at 500 hPa for initial basic states:(a)Matsa;(b)Meari 1.Red arrow indicates the warm advection,the blue arrow indicates the cold advection,and the white arrow indicates the boundary of warm and cold advections

对其他四个个例我们也进行了同样的分析，结果显示，垂直积分能量方案下的敏感区往往位于两个或多个系统的交界处，这揭示了其他系统对台风的引导作用，即环境场对台风的影响。此外，敏感区内流场都具有随高度顺转的特点，且总是位于冷暖平流的交界区，这说明该地区的稳定性相对较差；其次，在静力平衡和地转平衡近似下，根据热成风理论（朱乾根等，2000），流场随高度顺转，那么该地区整个厚度层内的大气应该对应有暖平流，此时如果有冷平流出现，易破坏热成风平衡，出现不稳定现象，大气需重新调整风场和温度场，调整过程必然对台风的发展变化产生影响。这些都可解释所识别的敏感区之所以“敏感”的原因。

下面分析水平投影方案下的敏感区的物理意义。

仍以麦莎和米雷1为例，进行详细分析。首先考查麦莎个例，对比图2、图4和图6可知，水平投影方案下的敏感区主要位于台风的东南部的环流场内，敏感区内流场也具有随高度顺转的特点（从气旋式曲率变为反气旋式曲率），低层暖平流较弱，高层暖平流较明显，此外，敏感区内有较强的垂直运动。接着考查米雷1个例，水平投影方案下的敏感区主要分为两部分，一部分位于台风的东北角，比能量方案下的靠东部分的敏感区偏南，另一部分位于台风的西南侧，台湾岛的东南角。分析其上的环流场可知，两块区域内流场也有随高度顺转的特点，且整个垂直层内都有明显的暖平流。两块敏感区有较大部分落入强垂直运动区内。可见，两个个例水平投影方案确定的敏感区的共同点是其上流场随高度顺转，且有暖平流，说明敏感区处于热成风平衡状态，然而敏感区内都有较强的垂直运动，台风环流中强烈的垂直运动也是影响台风发展变化的重要因素之一，可见该敏感区可在一定程度上反映出台风自身的对流不对称结构对台风发展变化的影响。其他四个个例的分析得到了类似的结果。

综上可见，能量方案确定的敏感区更多地揭示了环境场的作用及环境场与台风之间的相互作用，而水平投影方案确定的敏感区则可在一定程度上反映台风自身的对流不对称结构的影响。因此，不论用哪种方案，用CNOP的大值区去确定敏感区都有物理意义。

3.5 敏感区的有效性分析

我们通过理想回报试验来考查敏感区的有效性。

如前所述，CNOP可以看成是某种初始误差场，该初始误差场经过非线性或线性发展后使得预报误差最大。而我们确定敏感区的依据也是为了最大程度消除这种会导致最大预报误差的初始误差，使预报效果尽可能的好。那么在哪种方案确定的敏感区上消除误差可以最大程度消除CNOP型初始误差，使预报效果提高更明显呢？为此，我们在上述三种方案确定的敏感区里将CNOP型初始误差减小至原先的1/2，检验其对预报效果的改善情况。

首先，我们从验证区域内预报误差的能量的减小情况来考查，采用如下公式：

这里，J1表示由CNOP型初始误差δX0引起的验证区域里的预报误差。度量范数C2取为干能量，如（6）式表示。W为权重算子，在敏感区里取0.5，其余地方取 1。这样，J2表示在敏感区里减小初始误差后所引起的验证区域里的预报误差，因此，敏感区里的误差减小带来的预报效果的提高可以用(J1-J2)/J1表示。

表1给出了在不同方案确定的敏感区里减小误差对验证区域内预报误差能量的减小程度（百分比表示）。由表可见，六个个例均是在用垂直积分能量方案确定的敏感区里减小初始误差对预报效果的提高最显著，单点能量投影方案的次之，水平投影方案的最差。

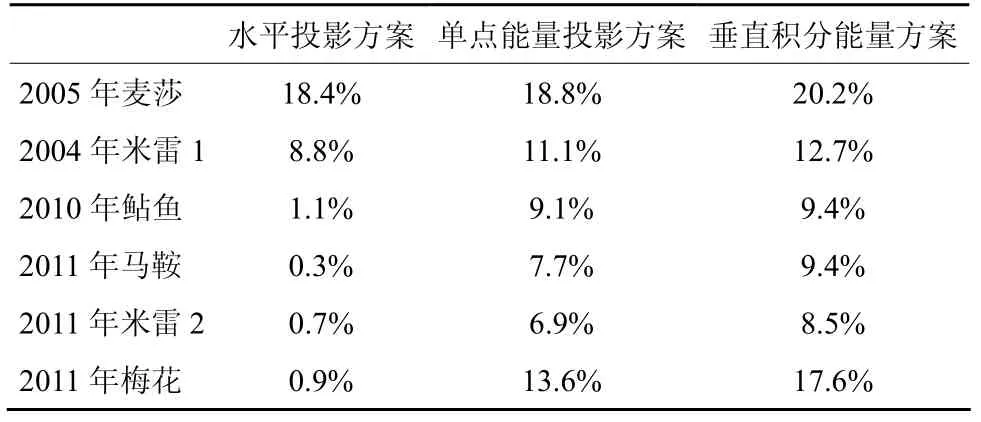
表1 分别在不同方案确定的敏感区里减小误差对预报误差能量的减小程度（百分比表示） Table 1 The reductions of forecast-error energies(in percent)obtained from the reductions of the initial errors in the sensitive areas identified by three schemes

其次，我们将进一步从台风的路径和强度的预报误差的减小方面来考查三种方案所确定的敏感区的有效性。采用类似（8）和（9）的公式，但这里目标函数J分别取为路径预报误差和最小海平面气压（强度）预报误差。

由表2可见，在水平投影方案确定的敏感区内减小误差对路径预报的改善都很小，对麦莎、米雷1以及马鞍这三个个例，两种能量方案确定的敏感区对路径预报效果的改善也较小，但对于鲇鱼、米雷2和梅花这三个个例，在两种能量方案确定的敏感区内减小初始误差都能使得路径预报技巧有较大的提高。进一步分析发现，麦莎、米雷1和马鞍这三个个例由初始误差导致的 24小时路径预报误差较小，都在90 km以内，而鲇鱼、米雷2和梅花这三个个例由初始误差导致的 24小时路径预报误差则较大，都在100 km以上（表3）。因此正如Qin et al.（2013）所指出，只有当原有预报误差较大的时候，CNOP方法识别的敏感区的优越性才能被体现出来。而在原有预报误差较大时，两种能量方案识别的敏感区对路径预报效果的改善要大于水平投影方案识别的敏感区，这一方面说明改善台风与环境场相互作用区的初始场能够较大程度地改善台风的路径预报，同时也说明台风路径的发展变化主要受环境场的影响。

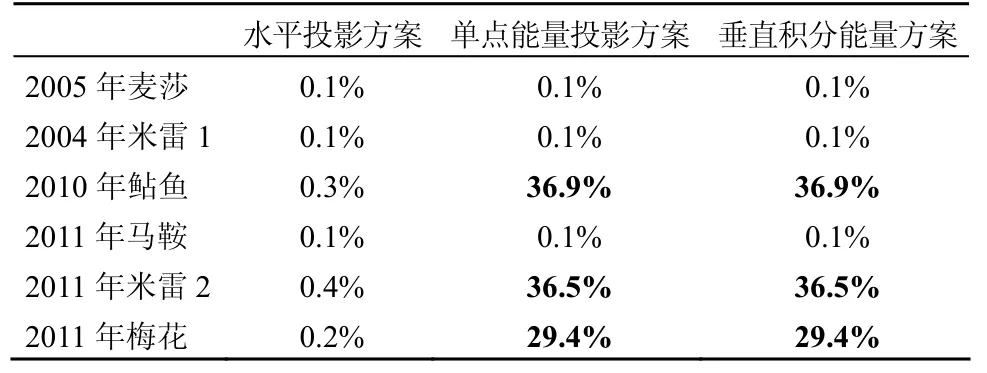
表2 分别在不同方案确定的敏感区里减小误差对24小时路径误差的减小程度（百分比表示） Table 2 The reductions of track forecast errors(in percent)obtained from the reductions of the initial errors in the sensitive areas identified by three schemes

表3 CNOP类型初始误差导致的24小时路径预报误差 Table 3 The 24-h track forecast errors caused by CNOP type of initial errors

以最小海平面气压表示台风的强度，表4给出了不同方案确定的敏感区里减小初始误差对 24小时台风强度预报误差的减小程度。正值表示预报技巧变好，负值表示预报技巧变差。由表4可见，六个个例中，在能量投影方案识别的敏感区内减小初始误差对强度预报有改善的台风个例有3个，分别为麦莎、鲇鱼和米雷 2；在水平投影方案识别的敏感区内减小初始误差对强度预报有改善的台风个例也有3个，分别为马鞍、米雷2和梅花。在改善程度上两种能量方案是相当的，其中，对于麦莎和鲇鱼个例，垂直积分能量方案略好，对于米雷2个例，单点能量投影方案较优，对于马鞍和梅花个例，则是水平投影方案要好。可见，在强度预报方面，三种方案的效果是因个例而异的。没有哪种方案显示出绝对的优势。

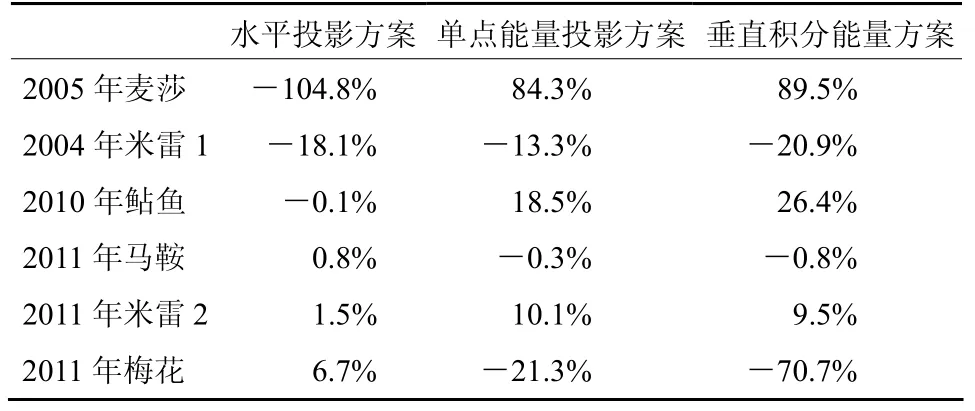
表 4 分别在不同方案确定的敏感区里减小初始误差对 24小时台风强度预报误差（最低海平面气压）的减小程度（百分比表示） Table 4 The reductions of intensity forecast errors(in percent,%)obtained from the reductions of the initial errors in the sensitive areas identified by three schemes

这也说明，强度预报技巧受到的影响因素更为复杂，更具有个例依赖性，若仅仅改善初始场中环境场的作用信息或台风的不对称结构信息，对台风强度预报的改善是较为有限的，正如前人所指出，要提高台风的强度预报技巧，改进模式的物理过程更为重要。此外，表4中也出现了不少负值，也即强度预报技巧变差的情况，对于当前的目标函数设置，这是可能的，正如Zhou and Mu（2011）所指出，在以能量为目标函数的情况下，CNOP识别的敏感区对预报技巧的改善只能从整体上而言，并不能保证每一个格点上每一个物理量的预报误差都是减小的。因此，也不能保证最小海平面气压的预报误差也是减小的。因此，发展更为有效的目标函数及其相应的优化求解办法，以保证台风强度和路径预报技巧的提高是今后重要的工作之一。

综上可见，在验证区域内预报误差能量的减小以及路径预报误差减小方面，两种能量方案，特别是垂直积分能量方案确定的敏感区比水平投影方案确定的敏感区有效；而在强度预报误差减小方面，三种方案效果是因个例而异、是相当的。因 此，总体而言，由垂直积分能量方案确定的敏感区对预报技巧改善更大。所以我们推荐在用 CNOP 方法确定敏感区时，采用垂直积分能量方案。这里需指出，鉴于目前在求解CNOP过程中，目标函数通常取为能量形式，所以本文主要考虑在以能量 为目标函数的情况下，所求取的 CNOP应该用何 种方案去确定敏感区较好。这种目标函数的选取可能会在一定程度上决定了我们的结果（即总体而 言能量方案确定的敏感区要好）。然而这需要再设计大量的数值试验去检验，我们将在今后的工作中展开。

4 总结与讨论

本文详细研究了如何用 CNOP方法确定敏感区。在台风目标观测以及台风的可预报性研究中，敏感区的确定至关重要。敏感区是台风目标观测中需额外增加观测的区域，其分布一方面决定了额外观测是否容易开展，另一方面也影响了该次额外观测的实施能在多大程度上改善台风的预报初值，进而关系到台风预报技巧的提高程度。因此可以说敏感区的确定关系到目标观测开展的价值，关系到台风的预报技巧能在多大程度上得以改善，是台风目标观测和台风可预报性研究的关键问题之一。虽然已有不少文献介绍了各种敏感区的识别方法（见引言），然而它们一般都只是较为简便地以各种方法得到的结果在垂直方向上进行积分，然后将得到的“大值区”作为敏感区。事实上，各种方法得到的结果，在对其进行处理时，由于采用了不同的衡量标准，其最后得到的“大值区”将可能具有较大的差别。而这一点在以往的文献中都没有深入的研究。鉴于敏感区的分布偏差将对目标观测和台风预报产生较大的影响，因此本文针对CNOP方法，深入讨论了对CNOP方法得到的结果进行各种不同处理而得到的大值区（也即敏感区）的分布区别及在其上减小初始误差对台风预报产生的影响。

具体的，本文针对CNOP方法，给出了三种敏感区的确定方案，分别命名为水平投影方案、单点能量投影方案以及垂直积分能量方案。应用这三种方案，分别确定了六个台风个例的敏感区。比较了各种方案确定的敏感区的差别，分析了各种敏感区所阐释的物理意义，讨论了它们的优缺点，并通过理想回报试验考查了不同方案确定的敏感区的有效性。结果显示，单点能量投影方案与垂直积分能量方案下识别的敏感区较为相似，二者与水平投影方案确定的敏感区则有较大的区别。两种能量方案确定的敏感区更多地反映了环境场对台风的影响，而水平投影方案则反映了台风自身对流不对称性结构对台风发展变化的影响。理想回报试验结果表明，由垂直积分能量方案和单点能量投影方案确定的敏感区对验证区域内预报误差能量的减小以及路径预报误差减小方面有效性要大于水平投影方案，而在强度预报误差减小方面，三种方案效果对个例依赖性明显、平均来讲是相当的。因此，总体而言，由垂直积分能量方案确定的敏感区对预报技巧改善更大。所以我们推荐在用CNOP方法确定敏感区时，采用垂直积分能量方案。

另一方面，由于不同方案揭示了不同的影响因素，因此，在台风目标观测应用中，如果能够事先对影响台风的主要因素有所判断，那么据此相应地采用不同的敏感区确定方案，则能使得识别的敏感区更为有效，可以更大程度地提高预报技巧。

由本文的分析也可见，之所以在以往的研究中，有些个例用垂直积分能量方案确定的敏感区的有效性不如其他区域，可能是这些个例其主要影响因素非环境场。此外，还有可能是当前所用的能量形式的目标函数不能较好地反应我们要考查的物理问题，因此发展更为有效的目标函数及其相应的优化求解办法是急需的。再者，正如穆穆（2013）所指出，“迄今为止，没有任何一种目标观测方法能够保证每一次目标观测都一定能够提高预报技巧。这里原因是多方面的。首先，模式总是有误差的，这种误差有时会导致敏感区确定出现偏差。其次，资料同化系统的不完善，也会使得不能有效地使用目标观测资料。还有，任何时候，我们只能知道观测资料的统计信息，而不能确切知道误差。”正因为存在着这种种的客观原因，使得敏感区的有效性会降低。但总的说，用CNOP的大值区作为敏感区，不论具体采取哪种方案都是有物理意义的，是可行的。具体方案的选取可因实际物理问题而定。在台风目标观测研究中，我们推荐使用垂直积分能量方案。

此外补充说明的是，目标观测的“敏感区”思想可以应用到资料同化中。当前我们有着浩瀚的资料，要同化各种各样且分布在宽广地域的资料将十分费时费力。因此，可以像目标观测那样，寻找资料的敏感性区域，如果只同化敏感区内的资料得到的预报初值其精确程度不亚于同化更多甚至所有区域内的资料而得的预报初值的精度，那么寻找敏感区对资料同化也将是尤为重要，而 Wang et al.①Wang Bin,Liu Juanjuan,Lu B.2013.An orthogonal expansion of filtering function in localization[J].To be submitted.的工作证明在资料同化中确实也存在资料的敏感区。可见，敏感区的确定还具有重要的应用价值，值得更多的学者开展相关的研究。

References)

Baker N L,Daley R.2000.Observation and background adjoint sensitivity in the adaptive observation-targeting problem[J].Quart.J.Roy.Meteor.Soc.,126(565): 1431-1454.

Birgin E G.,Martínez J E,Raydan M.2001.Algorithm 813: SPG-software for convex-constrained optimization[J].ACM Transactions on Mathematical Software,27(3): 340-349.

Bishop C H,Toth Z.1999.Ensemble transformation and adaptive observations[J].J.Atmos.Sci.,56(11): 1748-1765.

Bishop C H,Etherton B J,Majumdar S J.2001.Adaptive sampling with the ensemble transform Kalman filter.Part I: Theoretical aspects[J].Mon.Wea.Rev.,129(3): 420-436.

Buizza R,Cardinali C,Kelly G,et al.2007.The value of observations.Part II: The value of observations located in singular-vector-based target areas[J].Quart.J.Roy.Meteor.Soc.,133(628): 1817-1832

Chan J C L,Gray W M.1982.Tropical cyclone movement and surrounding flow relationship[J].Mon.Wea.Rev.,110(10): 1354-1376.

Chen Boyu,Mu Mu.2012.The roles of spatial locations and patterns of initial errors in the uncertainties of tropical cyclone forecasts[J].Adv.Atmos.Sci.,29(1): 63-78.

陈联寿,徐祥德,解以扬,等.1997.台风异常运动及其外区热力不稳定非对称结构的影响效应[J].大气科学,21(1): 83-90.Chen Lianshou,Xu Xiangde,Xie Yiyang,et al.1997.The effect of tropical cyclone asymmetric thermodynamic structure on its unusual motion[J].Chinese Journal of Atmospheric Sciences(Scientia Atmospherica Sinica)(in Chinese),21(1): 83-90.

Corbosiero K L,Molinari J.2003.The relationship between storm motion,vertical wind shear,and convective asymmetries in tropical cyclones[J].J.Atmos.Sci.,60(2): 366-376.

Duan W S,Zhang R.2010.Is model parameter error related to a significant spring predictability barrier for El Niño events? Results from a theoretical model[J].Adv.Atmos.Sci.,27(5): 1003-1013.

Duan W S,Mu M,Wang B.2004.Conditional nonlinear optimal perturbations as the optimal precursors for El Niño-Southern Oscillation events[J].J.Geophys.Res.,109(D23): D23105,doi:10.1029/ 2004JD004756.

Duan W S,Xu H,Mu M.2008.Decisive role of nonlinear temperature advection in El Niño and La Niña amplitude asymmetry[J].J.Geophys.Res.,113(C1): C01014,doi:10.1029/2006JC003974.

Duan W S,Xue F,Mu M.2009.Investigating a nonlinear characteristic of El Niño events by conditional nonlinear optimal perturbation[J].Atmos.Res.,94: 10-18.

Dudhia J.1993.A nonhydrostatic version of the Penn State/NCAR Mesoscale Model: Validation tests and simulation of an Atlantic cyclone and cold front[J].Mon.Wea.Rev.,121(5): 1493-1513.

Emanuel K,DesAutels C,Holloway C,et al.2004.Environmental control of tropical cyclone intensity[J].J.Atmos.Sci.,61(7): 843-858.

Fiorino M,Elsberry R L.1989.Some aspects of vortex structure related to tropical cyclone motion[J].J.Atmos.Sci.,46(7): 975-990.

Hamill T M,Snyder C.2002.Using improved background-error covariances from an ensemble Kalman filter for adaptive observations[J].Mon.Wea.Rev.,130(6): 1552-1572.

Hamill T M,Snyder C,Morss R E.2000.A comparison of probabilistic forecasts from Bred,singular-vector,and perturbed observation ensembles[J].Mon.Wea.Rev.,128(6): 1835-1851.

李英,陈联寿,王继志.2004.登陆热带气旋长久维持与迅速消亡的大尺度环流特征[J].气象学报,62(2): 167-179.Li Ying,Chen Lianshou,Wang Jizhi.2004.The diagnostic analysis on the characteristics of large scale circulation corresponding to the sustaining and decaying of tropical cyclone after its landfall[J].Acta Meteorologica Sinica(in Chinese),62(2): 167-179.

梁旭东,端义宏,陈仲良.2002.登陆台风对流和非对称结构[J].气象学报,60(增刊): 26-35.Liang Xudong,Duan Yihong,Chen Zhongliang,et al.2002.Convection and asymmetric distribution on landing tropical cyclone[J].Acta Meteorologica Sinica(in Chinese),60(Suppl.): 26-35.

孟智勇,徐祥德,陈联寿.1998.台湾岛地形诱生次级环流系统对热带气旋异常运动的影响机制[J].大气科学,22(2): 156-168.Meng Zhiyong,Xu Xiangde,Chen Lianshou.1998.Mechanism of the impact of the cyclone system induced by the Taiwan island topography on tropical cyclone unusual motion[J].Chinese Journal of Atmospheric Sciences(Scientia Atmospherica Sinica)(in Chinese),22(2): 156-168.

穆穆.2013.目标观测的方法、现状与发展展望[J].中国科学：地球科学,43(11): 1717-1725.Mu Mu.2013.Methods,current status,and prospect of targeted observation[J].Science in China：Earth Sciences,doi: 10.1007/s11430-013-4727-x.

穆穆,姜智娜.2007.集合预报初始扰动产生的一个新方法: 条件非线性最优扰动[J].科学通报,52(12): 1457-1462.Mu Mu,Jiang Zhina.2007.A new method for producing initial perturbation for ensemble forecast: Conditional nonlinear optimal perturbation[J].Chinese Science Bulletin(in Chinese),52(12): 1457-1462.

Mu M,Duan W S,Wang B.2003.Conditional nonlinear optimal perturbation and its applications[J].Nonlinear Processes in Geophysics,10: 493-501.

穆穆,王洪利,周菲凡.2007.条件非线性最优扰动方法在适应性观测研究中的初步应用[J].大气科学,31(6): 1102-1112.Mu Mu,Wang Hongli,Zhou Feifan.2007.A preliminary application of conditional nonlinear optimal perturbation to adaptive observation[J].Chinese J.Atmos.Sci.(in Chinese),31(6): 1102-1112.

Mu M,Sun L,Dijkstra H A.2004.The sensitivity and stability of the ocean’s thermohaline circulation to finite-amplitude perturbations[J].J.Phys.Oceanogr.,34(10): 2305-2315.

Mu M,Xu H,Duan W S.2007.A kind of initial errors related to “spring predictability barrier” for El Niño events in Zebiak-Cane model[J].Geophys.Res.Lett.,34(3): L03709,doi:10.1029/2006GL027412.

Mu M,Zhou F F,Wang H L.2009.A method for identifying the sensitive areas in targeted observations for tropical cyclone prediction: Conditional nonlinear optimal perturbation[J].Mon.Wea.Rev.,137(5): 1623-1639.

Palmer T N,Gelaro R,Barkmeijer J,et al.1998.Singular vectors,metrics,and adaptive observations[J].J.Atmos.Sci.,55(4): 633-653.

Pu Z X,Kalnay E.1999.Targeting observations with the quasi-inverse linear and adjoint NCEP global models: Performance during FASTEX[J].Quart.J.Roy.Meteor.Soc.,125(561): 3329-3337.

Qin Xiaohao,Mu Mu.2011a.Influence of conditional nonlinear optimal perturbations sensitivity on typhoon track forecasts[J].Quart.J.Roy.Meteor.Soc.,138(622): 185-197.

Qin Xiaohao,Mu Mu.2011b.A study on the reduction of forecast error variance by three adaptive observation approaches for tropical cyclone prediction[J].Mon.Wea.Rev.,139(7): 2218-2232.

Qin Xiaohao,DuanWansuo,Mu Mu.2013.Conditions under which CNOP sensitivity is valid for tropical cyclone adaptive observations[J].Quart.J.Roy.Meteor.Soc.,doi:10.1002/qj.2109

Rivière O,Lapeyre G,Talagrand O.2008.Nonlinear generalization of singular vectors: Behavior in a baroclinic unstable flow[J].J.Atmos.Sci.,65(6): 1896-1911.

Sun L,Mu M,Sun D J,et al.2005.Passive mechanism of decadal variation of thermohaline circulation[J].J.Geophys.Res.,110(C7): C07025,doi:10.1029/2005JC002897.

Tan Xiaowei,Wang Bin,Wang Dongliang.2010.Impact of different guidances on sensitive areas of targeting observations based on the CNOP method[J].Acta Meteor.Sinica,24(1): 17-30.

Terwisscha van Scheltinga A D,Dijkstra H A.2008.Conditional nonlinear optimal perturbations of the double-gyre ocean circulation[J].Nonlinear Processes in Geophysics,15: 727-734.

Wang Bin,Tan Xiaowei.2009.A fast algorithm for solving CNOP and associated target observation tests[J].Acta Meteor.Sinica,23(4): 387-402.

Zhou F F,Mu M.2011.The impact of verification area design on tropical cyclone targeted observations based on the CNOP method[J].Adv.Atmos.Sci.,28(5): 997-1010,doi:10.1007/s00376-011-0120-x.

Zhou F F,Mu M.2012a.The impact of horizontal resolution on the CNOP and on its identified sensitive areas for tropical cyclone predictions[J].Adv.Atmos.Sci.,29(1): 36-46,doi:10.1007/s00376-011-1003-x.

Zhou F F,Mu M.2012b.The time and regime dependencies of sensitive areas for tropical cyclone prediction using the CNOP method[J].Adv.Atmos.Sci.,29(4): 705-716.doi:10.1007/s00376-012-1174-0.

朱乾根,林锦瑞,寿绍文,等.2000.天气学原理与方法(第三版)[M].北京: 气象出版社.Zhu Qian’gen,Lin Jinrui,Shou Shaowen,et al.2000.Synoptic Meteorology Principles and Methods(3rd ed.)[M].Beijing: China Meteorological Press.

Zou X L,Vandenberghe F,Pondeca M,et al.1997.Introduction to adjoint techniques and the MM5 adjoint modeling system[R].NCAR Tech.Note,NCAR/TN-435_STR.