基于动态吸附模型的煤岩吸附气含量测井计算新方法
葛祥,何传亮,董震
(中石化西南石油工程有限公司测井分公司,四川 成都610100)
0 引 言
煤层吸附气量的定量计算是煤层气储层评价的关键和主要技术难题,利用测井资料计算其含量成为重要途径。为此,国内外开展了煤岩吸附气量的一系列计算方法研究并建立了一些计算模型[1-4],包括Langmuir等温吸附模型、Freundlich模型[5]、中子增量模型[6]、BP神经网络模型[7]等,其中兰氏方程应用最广泛。它们普遍为基于实验条件下的煤岩吸附气含量计算模型,在实际应用中存在一定局限性。首先是实验室条件不同于煤岩埋藏的实际情况,实验模型不能反映其动态变化特征;其次是已有实验模型考虑的因素较少,导致计算误差较大。因此,现有模型的应用条件较为苛刻,适用范围有限,不利于准确评价煤岩吸附气含量。
本文在实验支持下定量研究了地层条件下多种因素对煤岩吸附气含量的影响,将实验室的地面条件参数转换到地层条件下,建立了基于测井资料的计算煤岩吸附气量的动态吸附模型,提高了吸附气量的计算精度,在延川南等地区应用效果显著。
1 煤层气等温吸附模型
准确计算煤层的吸附含气量,关键要建立能真实反映原状煤层条件下气体吸附特征的吸附模型。国内外许多研究者对干燥煤和饱和(平衡)水分煤吸附甲烷的等温线模型进行了大量研究[8-9],以下是几种常见的等温吸附模型。
(1)Freundlich模型。根据Freundlich模型,吸附质(煤层气)与吸附剂(煤质)应存在相关性。

式中,V为吸附含气量,cm3/g(或 m3/t);m为吸附剂质量,g;x为被吸气体物质的量或指定状态下的体积,cm3;p为压力,MPa;n和k为经验常数。
通过Freundlich经验式将煤质分析结果(煤岩样品成分)和含气量联系起来,用实验室测定的纯煤含量(Vfc+Vdaf)代替煤质(吸附剂)含量,则式(1)可转变为

式中,k1为经验常数;ρ为煤质密度;Vfc为煤质中固定碳含量;Vdaf为煤质中挥发分含量。纯煤含量及煤质密度可以通过密度等测井资料求取。
Freundlich经验式可较好地应用于单分子吸附(属于I类等温线),特别是中压范围,不足之处是形式较为简单,式中常数没有明确的物理意义,不能说明吸附作用的机理。
(2)Langmuir模型(兰氏模型)。通过对吸附理论模型的研究分析可知,研究区内煤层对甲烷等气体的吸附主要适用于I型的Langmuir方程,可以通过实验室测试数据进行回归分析,并通过Langmuir等温吸附模型(也称兰氏模型)对含气量进行预测。

式中,V为吸附含气量,m3/t;兰氏体积VL是衡量煤岩吸附能力的量度,其值反映了煤的最大吸附能力,m3/t;pL为兰氏压力,即煤对甲烷吸附量达到兰氏体积一半时所对应的压力,MPa。
在实际计算过程中,考虑到煤岩中含有灰分等非碳组分,通常将煤质组分和含气量联系起来建立兰氏吸附等温线方程,同时考虑了实际状态下的温度(埋深)影响
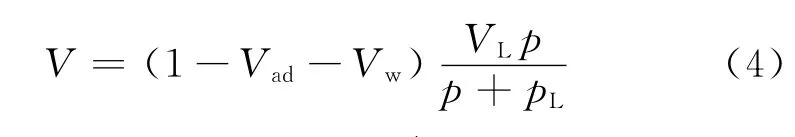
式中,Vad为煤质中灰分含量,%;Vw为煤质中水分含量,%。
(3)其他吸附理论。除单分子层吸附模型外,还有基于多分子吸附层的BET方程以及微孔填充吸附理论(D-R方程)、BET方程改进型、D-A方程、Kelvin方程(通常会出现Ⅳ和Ⅴ型等温线)等。等温线的性质多种多样,有时是几种类型的混合。
(4)已有吸附模型的局限。原状地层下煤层在不同压力、不同煤阶、不同孔隙特征及不同含水量的情况下,其等温吸附特性较为复杂,但目前对于煤层中水分含量介于0和饱和水分之间的吸附等温线仍主要用Langmuir吸附模型,也就是I型等温线表达。
兰氏方程在描述煤吸附甲烷等温线方面也存在不足:首先,模型假定的吸附方式为单分子层吸附,而实际在低温或者高压条件下也可以发生多分子层吸附;其次,模型假定固体吸附表面为均匀的,各处吸附能力相同,但实际地下的煤层并非如此。煤岩在不同深度处的温度、压力的变化会导致单分子层吸附的条件发生变化,即使在同一深度(温度)下,不同煤阶的纯煤质其吸附能力也存在差异。
2 吸附气含量影响因素
煤岩吸附气含量影响因素多样而复杂[10-11]。宏观来看,煤质组分、煤阶、压力(埋深)、温度等影响为主要因素。从微观上分析,煤岩吸附特性、矿物成分、储集空间、渗透率等岩石物理性质是决定吸附能力的本质因素。针对煤层埋藏特点以及兰氏模型的应用局限性,本文主要从宏观特性上对地层条件下煤岩吸附气量的多种影响因素进行了分析。
(1)煤质含量的影响。煤质是作为吸附气的主要载体,煤岩中的纯煤含量越高,吸附气越多。煤岩中煤质含量的大小是吸附气含量的主控因素,准确估算煤质组分含量成为吸附气含量计算的首要前提。
(2)煤阶影响。煤阶是影响煤吸附能力的主要因素之一,不同煤阶煤层气吸附能力具有差异。通常在同样温度和压力(深度)条件下,煤岩吸附气含量随着煤阶的增加而增加;但是到一定程度(镜质体反射率Ro>2.2%),高阶煤吸附甲烷能力随Ro的增大而降低。在煤岩可燃基中,兰氏体积VL与反映煤阶的镜质体反射率Ro呈倒“U”关系;在Ro=2.2%左右,VL值达到顶峰(见图1)。
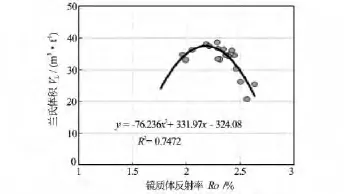
图1 兰氏体积VL与镜质体反射率Ro关系图
(3)埋深影响。在封盖条件较好的情况下,一定深度以下(延川南地区约1000m)随着埋深的增大,煤岩吸附气含量VL具有逐渐减小的趋势(见图2)。
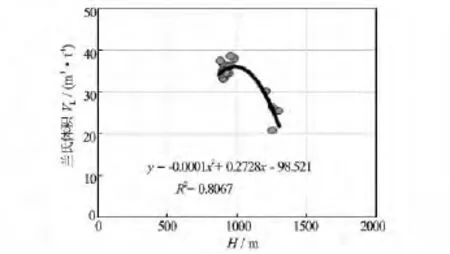
图2 兰氏体积VL与埋深H关系图
(4)温度变化影响。在延川南地区的煤岩吸附气含量VL随温度增加而逐渐下降,二者呈较好的线性关系,与埋深对煤岩吸附气含量的影响基本一致(见图3)。
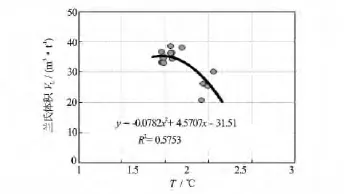
图3 兰氏体积VL与温度T关系图
(5)压力变化的影响。在等温吸附模型中,等温条件下煤对甲烷气体的吸附量VL与压力p应当呈正相关关系。在延川南地区实际资料的研究中,随着压力的增加,其吸附量的变化会出现2个阶段:第1个阶段的区间内(约p<6MPa)吸附气量随着压力增加而增加,吸附量趋于饱和状态;第2阶段(约p>6MPa后)吸附气含量受压力增加的影响较小,受埋深(温度)的影响更为明显,吸附量会随着深度的增加(温度升高)出现明显下降(见图4)。
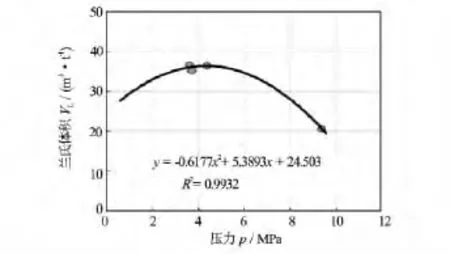
图4 兰氏体积VL与压力p关系图
3 动态吸附计算模型
煤岩的埋深(与温度影响基本一致)、压力、煤阶等变化会导致其吸附能力发生变化。基于实验分析及煤层气理论,在Langmuir等温吸附模型中考虑各参数的动态变化及煤质含量的影响建立煤岩吸附气量的动态吸附计算模型

式中,Vfc为固定碳含量,%;Ro为镜质体反射率,%;p为煤层压力,MPa;m、n为温度(或垂深)的影响因子。Vfc可利用测井解释的体积模型或者概率统计模型求解获得。F(Ro)为煤阶校正项,可根据测井参数进行多元回归拟合获得
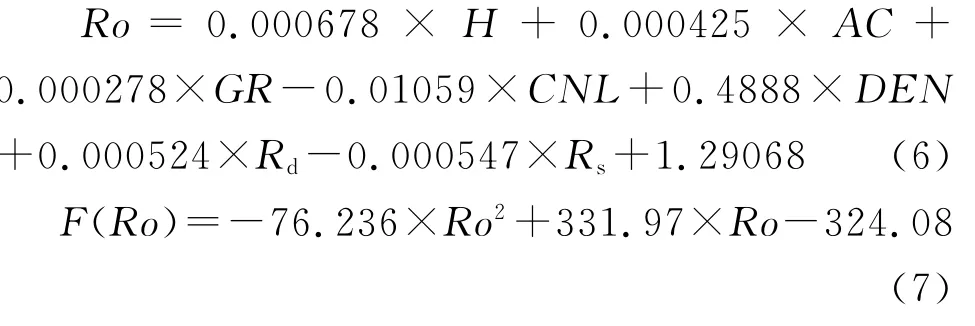
式中,H为深度,m;AC为声波时差,μs/ft*非法定计量单位,1ft=12in=0.3048m,下同;GR为自然伽马,API;CNL为中子孔隙度,%;DEN为体积密度,g/cm3;Rd、Rs分别为深、浅侧向电阻率,Ω·m。
m、n为影响因子(温度或垂深)与兰氏压力的回归系数,即pL=m×T+n。在拟合式中,温度影响因子更能反映煤层吸附特征的变化。
煤层压力p可直接与深度及测井参数建立回归关系

该动态计算模型根据研究区内的实测资料,对兰氏方程分别进行了煤层温度、压力、埋深、煤阶、煤质含量变化的校正,从各个影响因素上对煤岩等温吸附特征进行了动态描述,从而改善了兰氏方程在实际应用中的局限性。
4 应用效果分析
在延川南地区除了采用动态吸附模型外,还基于气体吸附理论和煤心刻度测井的方法建立了Freundlich经验拟合法、中子密度增量法及BP神经网络预测、Langmuir兰氏方程法等模型计算煤岩吸附气含量。图5中的右起第1道为Y3井2号煤层的动态吸附模型计算结果与煤心解析气量的对比,两者相关性较好,明显优于Freundlich经验拟合法(右起第5道)、中子密度增量法(右起第4道)及BP神经网络预测(右起第3道)、Langmuir兰氏方程法(右起第2道)的结果。
采用上述多套计算模型对延川南地区试验井的煤岩吸附气含量进行了计算。从Y3井2号煤层的计算结果(见表1)来看,动态吸附模型的计算结果略大于实验室解析含气量,其绝对误差最小,仅0.33m3/t,其他4种模型的计算结果均偏小,且Freundlich经验模型和中子-密度增量模型的绝对误差较大;动态吸附模型计算结果的相对误差最小(相对误差平均值为14.6%),兰氏模型的相对误差平均值也较小(16.4%),其他3种模型的相对误差明显较大(大于20%)。
综合比较认为,动态吸附模型在描述煤岩吸附能力方面具有更高的精度,计算结果更为可靠,具有较好的应用效果。
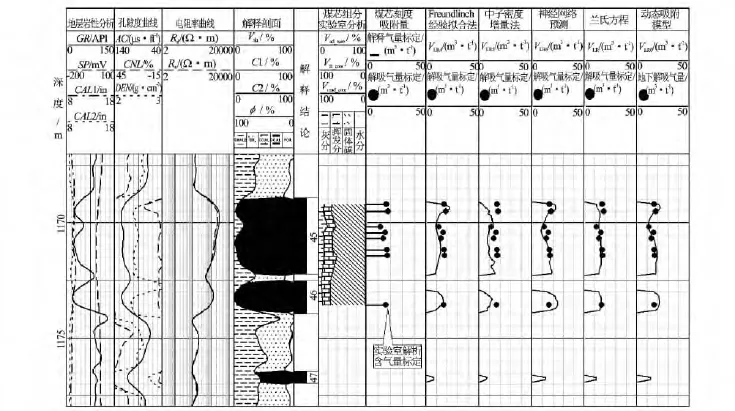
图5 Y3井2号煤层煤岩吸附气含量计算模型效果
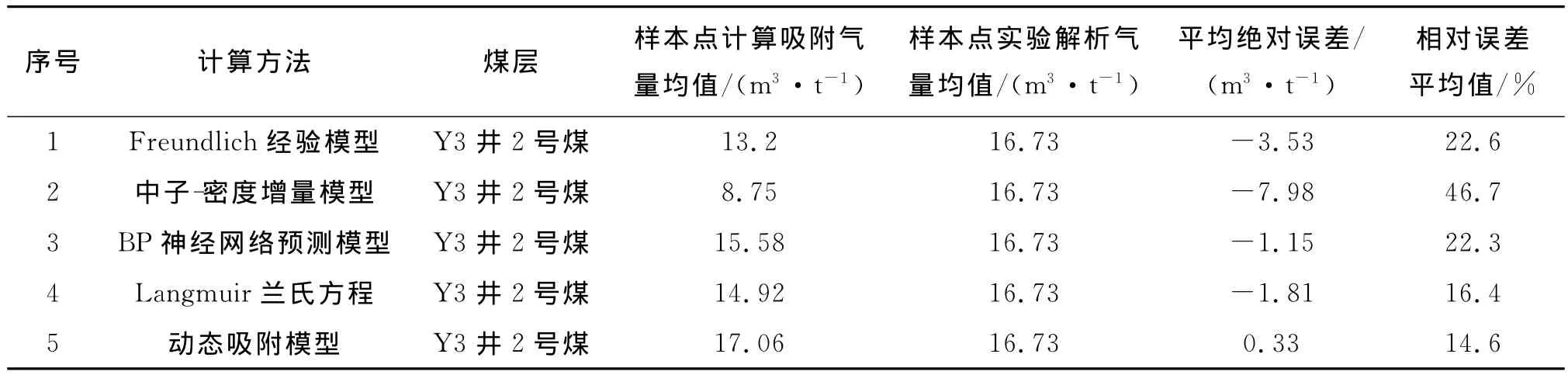
表1 延川南地区煤岩吸附气含量多模型计算效果比较
5 结 论
(1)利用测井资料结合煤心实验室分析数据对煤岩含气量进行预测是煤层气储层评价中较为有效的方法。
(2)相对于经典兰氏方程和其他计算方法,本文建立的计算煤岩吸附气含量的动态吸附模型更多地考虑了原状煤层的环境影响因素,包括煤层的煤质含量、煤阶、埋深(温度)、地层压力等,其结果能更好地反映原状煤层吸附能力的差异性。
(3)测井数据受井眼环境影响,其环境校正效果会影响到计算结果精度;计算模型参数的选取应根据不同的煤田实际资料统计得出。
[1]连承波,赵永军,李汉林,等.基于测井信息的煤层含气量预测方法[J].矿物学报,2007(Z1):446-447.
[2]王安龙,孙小琴,谢学恒.利用测井资料计算煤层含气量及工业组分方法研究[J].油气藏评价与开发,2011,1(1):69-73.
[3]潘和平,刘国强.依据密度测井资料评估煤层的含气量[J].地球物理学进展,1996,11(4):53-62.
[4]李贵红,张鸿,崔永君,等.基于多元逐步回归分析的煤储层含气量预测模型[J].煤田地质与勘探,2005,33(3):22-25.
[5]杨宗海.对Freundlich吸附等温式的理论推导的探讨[J].化学物理学报,1989,2(3):217-221.
[6]高绪晨.密度和中子测井对煤层甲烷含气量的响应及解释[J].煤田地质与勘探,1999,27(3):27-31.
[7]朱大奇,史慧.人工神经网络原理及应用[M].北京:科学出版社,2006:17-20.
[8]Btaeuer P,Salem M.Calculation of Single Adsorption Isotherms from Gravimetrically Binary Gas Mixture Adsorption Isotherms on Activated Carbon at High Pressures[J].Separation Purification Technology,1997,12:255-263.
[9]张庆玲,崔永君,曹利戈.煤的等温吸附实验中各因素影响分析[J].煤田地质与勘探,2004;32(2):16-19.
[10]赵毅,毛志强,蔡文渊,等.煤层气储层测井评价方法研究[J].测井技术,2011,35(1):54-57.
[11]贺天才,秦勇,张新民,王佟.煤层气勘探与开发利用技术[M].徐州:中国矿业大学出版社,2007.

