利用有效应力进行横波预测及其应用

尹成芳，柯式镇，彭斐，冯志勇

（1．中国石油大学（北京），北京102249；2．北京市地球探测与信息技术实验室，北京102249；3．北京中石大新元投资有限公司，北京102249；4．中国石油集团测井有限公司，陕西 西安710077）

0 引 言

油气勘探中，横波时差与纵波时差结合，利用纵横波时差比值可识别岩性、计算孔隙度［1］。在裂缝发育带，纵横波幅度衰减变大，可用来识别裂缝带，利用二者衰减程度不同，还可进一步判断裂缝角度。依据纵、横波能量衰减，纵波时差增大、纵波幅度衰减显著增大而横波幅度衰减减小，可用于评价气层［2］。横波时差与纵波时差、密度结合可更全面、准确地研究岩石力学性质，计算岩石弹性参数、井壁有效应力和进行岩石机械性质分析等。阵列声波测井仪还可利用横波分裂分析地层各向异性及其原因，确定最大主应力方向等。斯伦贝谢公司2006年投入商用的声波扫描测井仪还具备评价井壁周围三维空间机械特性、应力分布的能力［3］。另外，声波属性还可用于精确标定由于岩性不同、孔隙度不同、流体性质的差异等引起的地震振幅响应不同。由于国外横波测井仪器仍存在测井成本过高问题，而对于中国开发后期的井，多数没有横波资料，因此更准确预测横波，为岩石物理分析服务，仍是众多学者研究的重点。

近年发展起来的岩石物理模型越来越广泛，包括等效弹性模量计算模型 Hashin－Shtrikman［4］、Voigt［5］和 Reuss［6］、Berryman［7］等。针对这些经典模型，国内外学者进行了大量的研究和改进。楚泽涵等［8］参照Berryman散射模型，计算了复合介质的等效弹性模量，得出骨架矿物成分纯净时，会有较好的效果，若骨架矿物成分不够纯净，则必须经过校正。利用地震资料识别油气可行性分析的基础是流体替换，Gassmann方程［9］是适用于低频地震流体替换最基本公式，但该方法仅限于单矿物岩石，且对于实验室条件下超声波一般效果不好。Blangy等［10］在研究中发现湿润的黏土矿物会改变岩石的刚性。陈信平等［11］认为只要含有少量气体，流体的体积模量就会大大降低。这些都说明了Gassmann方程使用的局限性。为此，Berryman等［12］将Gassmann方程推广到2种孔隙类型的混合孔隙介质中。基于岩石物理模型进行横波预测，Xu－White等［13］提出了利用孔隙度和泥质含量估算泥质砂岩纵波和横波速度的模型。Gal等［14］对 Hashin－Shtrikman上边界进行了修正，提出了适用于低于30%孔隙度且压实的岩石的“孔隙一致减小”模型。Castagna等［15－16］利用测量的泥岩数据及实验室合成砂岩，得到了著名的“泥岩线”和饱含水砂岩纵横波速度关系式。Han［17］利用超声波数据也得到了类似的关系式。熊晓军等［18］提出了基于等效弹性模量反演的横波速度预测方法。这些模型中存在一些参数很难通过实验室获取，或者过于简化地层真实信息等问题，不确定性较大。

本文在前人研究基础上，采用地震岩石物理模型预测横波速度的方法，在该模型中，选择控制岩石体积模量的参数作为回归变量，不存在对典型未知参数的不可靠的假设条件，如孔隙空间形态的假设。回归变量选择的这种灵活性是该方法的一个重大优势。

1 地震岩石物理模型

地震岩石物理模型采用的基本公式［19］为

式中，M为体积模量或剪切模量；Mmod为模拟模量；M0为回归函数，M0＝m0exp（m1x1＋m2x2＋…），其值≥0，亦为体积模量和剪切模量的刻度参数，其输入是各矿物和流体模量，该参数也可以为常数；Mi为矿物模量；Mfluid为流体模量；φ为孔隙度；fi为矿物体积百分含量；mi为回归参数；xi为回归变量。该模型既适用于体积模量，也适用于剪切模量（流体剪切模量Mfluid＝0）。这里不需要像常规地震岩石物理模拟一样，预先预测干岩样弹性模量。采用Reuss、Voigt边界，当M0＜0时，令其值等于边界值，从而保证一阶导数的连续性。当无测量横波曲线时，保证该方法较传统方法更为稳定、可靠。为保证拟合的准确性，其质量控制采用测井曲线和岩心数据进行。

一般建立地震弹性参数与测井曲线之间关系时，采用的经验模型均与Reuss和Voigt边界或者Hashin－Shtrikman边界有关。建模最简单的方法是忽略边界，相当于采用最简单的回归函数或者神经网络方法。这样在给定曲线段，可得到较好结果，但是当用于模拟其他井段时，插值效果较差。通过增加边界条件，其效果可得到改善，但当回归曲线到达上边界或下边界时，易造成“假膝盖”现象。为此，最好的方法是利用边界条件指导插值，这样使得边界范围内的回归函数更为合理，从而代替简单的弹性模量所占百分比的情况。

如果回归函数选择与流体无关的参数，则岩石物理模型与Gassmann单矿物流体替换、Berryman双矿物流体替换一致，这也意味着不再需要根据矿物百分含量和孔隙分布假设有效矿物，从而使得地震岩石物理改进流体替换成为现实。

2 有效应力引入

对于疏松砂岩，利用声波计算的孔隙度明显偏高，而偏高的程度与岩石的压实程度有关，为此引入有效应力作为地震岩石物理模型回归变量，其回归函数为

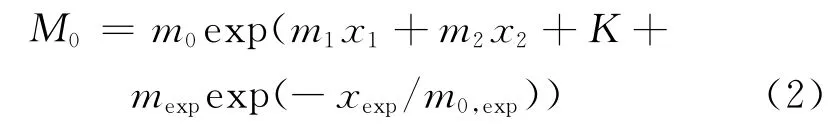
式中，xexp为有效应力。

有效应力是由上覆岩层压力pOB和孔隙压力pP计算得到［20］。上覆岩层压力主要由密度曲线计算得到，公式为

式中，g为重力加速度，m／s2；ρ（z）为深度z处的密度值。

利用声波曲线在泥岩中确定正常压实趋势线，根据Eaton公式［21］，预测孔隙压力为

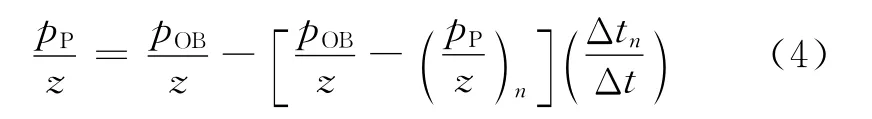
根据A1和A2井实际测试资料验证，预测的孔隙压力与实测资料吻合较好。

有效应力是上覆岩层压力与地层孔隙压力之间的差值

3 横波预测

基于地震岩石物理模型，利用各矿物百分含量、孔隙度、饱和度、混合流体体积模量和有效应力等作为岩石物理模型输入，其预测横波流程见图1。预测结果见图2，第1道模拟剪切模量与实测剪切模量吻合较好。这也说明，岩石物理模型较好地考虑到了压实、矿物、孔隙度及孔隙流体对弹性属性的影响。图2中第2道为没有有效应力建立的岩石物理模型模拟的剪切模量与实测剪切模量对比图。从图2可见，效果较包含有效应力作为岩石物理模型输入建立的岩石物理模型较差。作为衡量模拟弹性模量与实测弹性模量之间相对误差的参数在理想情况下，该值为0。增加变量的数量，该值会降低，但并不意味着改进了岩石物理模型。包含有效应力建立的岩石物理模型，模拟剪切模量的相对误差为0．1562，而没有有效应力的岩石物理模型，模拟剪切模量的相对误差为0．3211。包含有效应力建立的岩石物理模型预测的横波（见图2第3道）随深度的增加而增大，与校正后实测横波速度吻合度较高，而没有有效应力建立的岩石物理模型，预测的横波（见图2第4道）随深度的增加，增大趋势不明显。整体上讲，利用有效应力建立的岩石物理模型比缺少有效应力的模型更合理且具有更低的相对误差和更高的准确度。

图1 横波预测流程图

图2 包含有效应力与无有效应力预测剪切模量与横波对比图

利用建立的岩石物理模型，对已有横波资料的3口井，进行了横波预测和反刻度，分析认为预测横波与测量横波相比，准确度相对较高。同时利用建立的岩石物理模型，对无横波资料的其他5口井进行了横波预测。

4 预测横波应用

4．1 叠前反演

相比叠后反演，叠前反演的弹性阻抗与入射角、纵波、横波速度、密度4项参数有关。由于同时利用了纵速度、横波速度，其计算产生的弹性参数远丰富于叠后反演，可用于区别岩性，进行含油气性的识别，从而为钻探提供更丰富、更准确的依据。利用8口井纵波资料、密度资料及3口井实测横波资料和5口井预测横波资料进行反演。图3、图4分别为井点处波阻抗、纵横波速度反演结果与实测测井曲线的对比。蓝色曲线为反演结果，红色曲线为测井实测曲线，绿色曲线为低频曲线。对比可见，3口井的波阻抗反演结果与实测波阻抗曲线吻合得非常好，纵横波速度比反演结果除A2井和A3井在1．1s附近有个别尖峰吻合得差一点之外，其他井段吻合得也非常好。叠前反演成功地反演出了研究区内所有关键的砂层组，但个别的薄砂层由于地震分辨率有限，无法分辨，因此许多情况下反演中的薄砂层，实际是几个薄砂层组合的综合响应，不能与实测曲线一一对应。

4．2 岩石物理反演

图3 波阻抗反演结果

图4 纵横波速度比反演结果

岩石物理反演利用了岩石物理建模的反形式，即由已知的弹性属性反演岩石物理参数，如泥质含量和孔隙度，从而提供泥质含量和孔隙度的三维数据体。岩石物理模型标准输入有矿物模量、流体模量、孔隙度、泥质含量，用孔隙度、泥质含量等作为可能的回归变量。矿物模量在文献［22］中可查到，随温度、压力变化的各流体体积模量根据Batzle和Wang［23］计算得到，用Reuss公式计算各流体混合后体积模量，用含油饱和度、含气饱和度和含水饱和度作为权系数，这种权系数对于地震频率应该是有效的。目前常用的岩石物理反演方法是孔隙度饱和度联合反演方法。

用岩石物理反演技术建立岩石物理模型显示了模拟和测量的弹性属性之间很好的一致性，反演中测试了回归参数的多种不同组合用于优化最终的模型。

如图5所示分别为A1井、A2井、A3井孔隙度反演结果，与测井计算孔隙度曲线吻合较好。泥质含量反演效果没有孔隙度好，在某种相对意义上泥质含量反演的趋势也是合理的（见图6）。泥质含量反演结合孔隙度反演结果，可用于评价砂岩的相对含量，进而为将来钻井作业优选有利目标。

图5 孔隙度反演结果

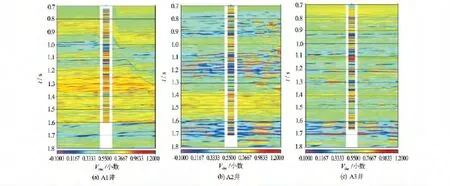
图6 泥质含量反演结果

5 结 论

（1）采用地震岩石物理模型，选择控制岩石体积模量的参数作为回归变量，不存在对典型未知参数的不可靠假设条件。当回归函数选择与流体无关的参数时，与Gassmann流体替换一致，而且拓展为多矿物流体替换。利用边界条件指导无测井曲线约束的插值，使边界范围内的回归函数更为合理。

（2）通过对比包含有效应力和无有效应力作为回归变量的岩石物理模型，包含有效应力模拟剪切模量的相对误差为0．1562，而没有有效应力的岩石物理模型相对误差为0．3211。包含有效应力建立的岩石物理模型预测的横波速度随深度的增加而增大，与校正后实测横波速度吻合度较高，而没有有效应力建立的岩石物理模型，预测的横波随深度的增加，增大趋势不明显。

（3）利用校正后3口井实测横波与预测5口井横波资料，进行波阻抗反演、纵横波速度比反演，结果均反映了关键的砂层组。孔隙度反演结果与测井计算孔隙度曲线吻合较好，而泥质含量反演效果没有孔隙度好，但在某种相对意义上趋势也是合理的。

［1］洪有密．测井原理与综合解释［M］．东营：中国石油大学出版社，1998．

［2］中国石油勘探与生产分公司．碳酸盐岩油气藏测井评价及应用［M］．北京：石油工业出版社，2009．

［3］Pabon J，Vivian Pistre，Kinoshita T，et al．A Modular Wireline Sonic Tool for Measurements of 3D （Azimuthal，Radial，and Axial Formation Acoustic Properties［C］∥The SPWLA 46th Annual Logging Symposium，2005．

［4］Hashin Z，Shtrikman S．A Variational Approach to the Theory of the Elastic Behavior of Multiphase Materials［J］．Journal of Mechanics and Physics Solids，1963，2：127－140．

［5］Voigt W．Lehrbuh der Kirstallphysik［M］．Teubner，Leipzig，1928．

［6］Reuss A．Berechnung Der Fliessgrense Von Mischkristallen Aufground Der Plastizitatbedingung Fur Einkristalle［J］．Zeitschrift Fur Angewandte Mathmatik Mechanik，1929，65：349－354．

［7］Berryman J G．Long－wavelength Propagation in Composite Elastic Media［J］．Acoust Soc Am，1980，68（B）：1809－1831．

［8］楚泽涵，陈丰，刘祝萍，等．估算地层横波速度的新方法［J］．测井技术，1995，19（5）：313－318．

［9］Gassmann F．Elastic Waved Through a Packing of Spheres［J］．Geophysics，1951，16（4）：673－685．

［10］Blangy J P，Strandenes S，Moor D，et al．Ultrasonic Velocities in Sand－revisited［J］．Geophysics，1993，58（2）：227－239．

［11］陈信平，刘素红．浅谈Gassmann方程［J］．中国海上油气：地质，1996，10（2）：122－127．

［12］Berryman J G，Milton G W．Exact Results for Generalized Gassmann’s Equation in Composite Porous Media with Two Constituent［J］．Geophysics，1991，56（12）：1950－1960．

［13］Xu S Y，White R E．A New Velocity Model for Claysand Mixture［J］．Geophysical Prospecting，1995，43：91－118．

［14］Doron Gal，Jack Dvorkin，Amos Nur．A Physical Model for Porosity Reduction in Sand Stones［J］．Geophysics，1998，63（2）：454－459．

［15］Castagna J P，Batzle M L，Eastwood R L．Relationships Between Compressional Wave and Shear Wave Velocities in Clastic Silicate Rocks［J］．Geophysics，1985，50：571－581．

［16］Castagna J P，Batzle M L，Kan T K．Rock Physics——the Link Between Rock Properties and AVO Response in Offset Dependent Reflectivity，Theory and Practice of AVO Analysis［C］∥Society of Exploration Geophysicists，Tulsa，Oklahoma，1993：135－171．

［17］Han D H．Effects of Porosity and Clay Content on Acoustic Properties of Sand Stones and Unconsolidated Sediments［D］．Stanford University，1986．

［18］熊晓军，林凯，贺振华．基于等效弹性模量反演的横波速度预测方法［J］．石油地球物理勘探，2012，47（5）：723－727．

［19］Kjetil Westeng，Henrik Juhl Hansen，Klaus Bolding Rasmussen．ISIS Rock Physics——A New Petro－elastic Model for Optimal Rock Physics Inversion with Examples from the Nini Field［C］∥ Sound of Geology Workshop 2009，Bergen Norway，the 6－8May，2009．

［20］周大晨．对上覆岩层压力计算公式的思考［J］．石油勘探与开发，1999，26（3）：119－123．

［21］Ben A Eaton．The Equation for Geopressure Prediction from Well Logs［C］∥SPE5544，1975．

［22］Gary Mavko，Tapan Mukerji．The Rock Physics Handbook：Tools for Seismic Analysis in Porous Media［M］．Cambridge：Cambridge University Press，1998．

［23］Batzle M，Wang Z．Seismic Properties of Pore Fluids［J］．Geophysics，1992，57（11）：1396－1408．